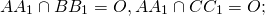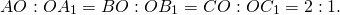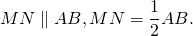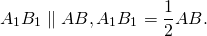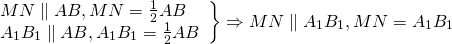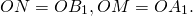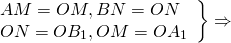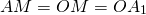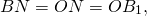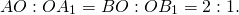Свойство медиан треугольника доказательство через векторы (6 видео)

Медиана треугольника

Определение . Медианой треугольника называют отрезок, соединяющий вершину треугольника с серединой противоположной стороны (рис 1).

Поскольку в каждом треугольнике имеется три вершины, то в каждом треугольнике можно провести три медианы.

На рисунке 1 медианой является отрезок BD .

Утверждение 1 . Медиана треугольника делит его на два треугольника равной площади ( равновеликих треугольника).

Доказательство . Проведем из вершины B треугольника ABC медиану BD и высоту BE (рис. 2),

и заметим, что (см. раздел нашего справочника «Площадь треугольника»)

Поскольку отрезок BD является медианой, то

что и требовалось доказать.

Утверждение 2 . Точка пересечения двух любых медиан треугольника делит каждую из этих медиан в отношении 2 : 1 , считая от вершины треугольника.

Доказательство . Рассмотрим две любых медианы треугольника, например, медианы AD и CE , и обозначим точку их пересечения буквой O (рис. 3).

Обозначим середины отрезков AO и CO буквами F и G соответственно (рис. 4).

Теперь рассмотрим четырёхугольник FEDG (рис. 5).

Сторона ED этого четырёхугольника является средней линией в треугольнике ABC . Следовательно,

Сторона FG четырёхугольника FEDG является средней линией в треугольнике AOC . Следовательно,

Отсюда вытекает, что точка O делит каждую из медиан AD и CE в отношении 2 : 1 , считая от вершины треугольника.

Следствие . Все три медианы треугольника пересекаются в одной точке.

Доказательство . Рассмотрим медиану AD треугольника ABC и точку O , которая делит эту медиану в отношении 2 : 1 , считая от вершины A (рис.7).

Поскольку точка, делящая отрезок в заданном отношении, является единственной, то и другие медианы треугольника будут проходить через эту точку, что и требовалось доказать.

Определение . Точку пересечения медиан треугольника называют центроидом треугольника.

Утверждение 3 . Медианы треугольника делят треугольник на 6 равновеликих треугольников (рис. 8).

Доказательство . Докажем, что площадь каждого из шести треугольников, на которые медианы разбивают треугольник ABC , равна площади треугольника ABC. Для этого рассмотрим, например, треугольник AOF и опустим из вершины A перпендикуляр AK на прямую BF (рис. 9).

Содержание

Свойство медиан треугольника
7 Comments
Свойства медианы треугольника. Итоговое повторение курса геометрии 7 – 9 класса
🎦 Видео

Видео:Теорема о точке пересечения медиан треугольника. Доказательство. 8 класс.Скачать

Свойство медиан треугольника

Свойство медиан треугольника может быть доказано многими способами. Доказательство, опирающееся на свойства параллелограмма и средней линии треугольника, может быть проведено сразу же после изучения соответствующих тем, что позволяет начать использовать свойство медиан треугольника уже с начала 8 класса.

(Свойство медиан треугольника)

Медианы треугольника пересекаются и в точке пересечения делятся в отношении 2:1, считая от вершины.

Дано : ABC, AA1, BB1, CC1 — медианы

1) Пусть M — середина отрезка AO, N — середина BO

(то есть AM=OM, BN=ON).

2) Соединим точки M, N, A1 и B1 отрезками.

3) Так как AA1 и BB1 — медианы треугольника ABC, точка A1- середина отрезка BC, B1 — середина AC.

Следовательно, A1B1 — средняя линия треугольника ABC и

Значит, четырёхугольник MNA1B1 — параллелограмм (по признаку).

По свойству диагоналей параллелограмма

из чего следует, что

5) Доказательство того факта, что все медианы треугольника пересекаются в одной точке, будем вести методом от противного.

Предположим, что третья медиана CC1 треугольника ABC пересекает медианы AA1 и BB1 в некоторой точке, отличной от точки O.

Тогда на каждой медиане есть две различные точки, делящие её в отношении 2:1, считая от вершины. Пришли к противоречию.

Таким образом, все три медианы треугольника пересекаются в одной точке и точка пересечения медиан делит каждую из их в отношении 2:1, считая от вершины:

Что и требовалось доказать .

Видео:8. Медиана треугольника и её свойства.Скачать

7 Comments

Промогите пожалуйста:
В прямоугольном треугольнике из вершины прямого угла до гипотенузы провели медиану длинной 50см и перпендикуляр 48см. Вычислить периметр.

Медиана, проведённая к гипотенузе, равна её половине. Следовательно, гипотенуза 100 см. Пусть катеты равны x см и y см. По теореме Пифагора x²+y²=100². Площадь треугольника равна половине произведения стороны на высоту, проведённую к этой стороне S=0,5∙100∙48 см², либо половине произведения катетов S=0,5∙x∙y. Отсюда xy=4800.
Решаем систему уравнений: x²+y²=100²; xy=4800. Решения (60;80) (80;60). То есть катеты 60 см и 80 см. Периметр P=60+80+100=240 см.
(Не обязательно доводить решение системы до конца. Достаточно найти x+y. Для этого к 1-му уравнению прибавим удвоенное 2-е, получим
x²+2xy+y²=19600; x+y=140).

Прошу помощи в решении задачи: на стороне ромба построен равносторонний треугольник. Отрезок, соединяющий точку пересечения диагоналей ромба с серединой стороны треугольника, составляет с ней угол 70 градусов. Найти острый угол ромба.

Во-первых, большое спасибо за решение, даже не ожидала ответа, но, по счастью, ошиблась! Но я к этому времени уже решила так:провела ВМ, которая в равностороннем треугольнике является также высотой.
Рассмотрим четырехугольник ОВМС: угол ВОС =углу ВМС=90 градусов (диагонали ромба взаимно перпендикулярны),отсюда, ВМ параллельна ОС, тогда угол МОС=20 градусам. Рассм. треугольник ОМС: угол МСО= 180-20-70=90 градусов, и одновременно= 60+x, т.о., угол х=30 градусам, и искомый острый угол ромба=60 градусам. Мы получили разные ответы, в чем может быть дело (окружности мы еще не проходили).

Наталия углы BOC и BMC не накрест лежащие и не внутренние односторонние, поэтому BM не параллельна OC. Но вариант решения без окружности возможен, добавила второй способ.

Видео:Как доказать теорему о медианах треугольника с использованием методов векторной алгебры?Скачать

Свойства медианы треугольника. Итоговое повторение курса геометрии 7 – 9 класса

Свойства медианы треугольника

Итоговое повторение курса геометрии 7 – 9 класса

При изучении какой-либо темы школьного курса можно отобрать определенный минимум задач, овладев методами решения которых, учащиеся будут в состоянии решить любую задачу на уровне программных требований по изучаемой теме. Предлагаю рассмотреть задачи, которые позволят увидеть взаимосвязи отдельных тем школьного курса математики. Поэтому составленная система задач является эффективным средством повторения, обобщения и систематизации учебного материала в ходе подготовки учащихся к экзамену.

Для сдачи экзамена не лишними будут дополнительные сведения о некоторых элементах треугольника. Рассмотрим свойства медианы треугольника и задачи, при решении которых этими свойствами можно воспользоваться. В предложенных задачах реализуется принцип уровневой дифференциации. Все задачи условно поделены на уровни (уровень указан в скобках после каждого задания).

Вспомним некоторые свойства медианы треугольника

Свойство 1. Докажите, что медиана треугольника ABC, проведённая из вершины A, меньше полусуммы сторон AB и AC.

Отложим на продолжении медианы AM за точку M отрезок MK, равный AM. Тогда в четырёхугольнике ABKC диагонали пересекаются и точкой пересечения делятся пополам. Значит, ABKC — параллелограмм. Применяя неравенство треугольника к треугольнику ABK, получим, что

то, сложив почленно эти три неравенства, получим, что

2AM + BN + CK > AB + BC + AC.

Отсюда следует, что AM + BN + CK > (AB + BC + AC).

Отложим на продолжении медианы AM за точку M отрезок MA1, равный AM. Тогда ABA1C — параллелограмм. Поэтому

BA1 = AC, 2AM = AA1 SDEF’ , то SAED+SBFD>SDEF , следовательно, указанным образом расположить точки невозможно.

так расположить точки нельзя.

Источник: Окружная олимпиада (Москва) , 2008 г, 11 класс

№32 Темы: Удвоение медианы. Ортоцентр и ортотреугольник Сложность:5 + Три точки, лежащие на одной прямой Подобные треугольники Классы: 9,10

В неравнобедренном треугольнике ABC точки H и M – точки пересечения высот и медиан соответственно. Через вершины A , B и C проведены прямые, перпендикулярные прямым AM , BM , CM соответственно. Докажите, что точка пересечения медиан треугольника, образованного проведенными прямыми, лежит на прямой MH .

Решение

Пусть A’B’C’ – треугольник, образованный

проведенными прямыми и G – точка пересечения его

медиан. Мы докажем, что M является серединой отрезка GH . Достроим треугольник BMC до параллелограмма BMCA1 . Отрезок MA1 делит сторону BC пополам, поэтому A1 лежит на прямой AM , причем AM = A1M (поскольку точка M делит медиану в отношении 2:1 ). Кроме того, BA1|| MC A’B’ и CA1|| MB A’C’ , поэтому BA1 и CA1 – высоты треугольника BA’C , значит A1 является ортоцентром треугольника BA’C , и

A’A1 BC . Стороны треугольника BA1M перпендикулярны

сторонам треугольника A’B’C’ соответственно, поэтому эти треугольники подобны, причем соответствующие прямые BC и

AG , содержащие медианы этих треугольников,

перпендикулярны. Значит, прямая A’G совпадает с прямой A’A1 . Пусть G’ – точка, симметричная точке H относительно M . Треугольники AHM и A1G’M симметричны относительно M , поэтому A1G’|| AH BC . Отсюда следует, что G’ лежит на прямой A’G . Аналогично, получаем, что G’ лежит на прямой B’G , то есть G’ совпадает с G .

Источник: Всероссийская олимпиада по математике, 2008 г, 9 класс

Отрабатываем умение: самостоятельно решать задачи.

Свойства медианы. Площадь треугольника

1. В треугольнике АВС медиана АМ перпендикулярна медиане BN. Найдите площадь треугольника АВС, если длина АМ равна 3, а длина BN равна 4.

2. Основание равнобедренного треугольника равно 2. Медианы, проведенные к боковым сторонам, взаимно перпендикулярны. Найдите площадь треугольника.

3. Две медианы равнобедренного треугольника взаимно перпендикулярны. Боковая сторона равна . Найдите площадь треугольника.

4. В треугольнике АВС медианы АD и ВE перпендикулярны, , . Чему равен квадрат третьей стороны?

5. Сторона треугольника равна 20, а медианы, проведенные к двум другим сторонам – 24 и 18. Найдите площадь треугольника.

6. Стороны треугольника равны 13, 14 и 15. Найти площади треугольников, на которые разбивается данный треугольник его медианами.

7. Площадь треугольника АВС равна 12. Из вершины тупого угла В проведена медиана BD, длина которой равна 3. Найдите длину стороны АС, если угол ABD – прямой.

8. Найдите площадь треугольника, если две его стороны равны 1 и , а медиана третьей стороны равна 2. (Указание – достроить до параллелограмма).

О т в е т: .

1. Одна сторона треугольника равна а, другая – b. Найдите третью сторону, если известно, что она равна медиане, проведенной к ней.

О т в е т: .

2. Основание равнобедренного треугольника , медиана боковой стороны 5. Найдите длины боковых сторон.

3. В равнобедренном треугольнике основание равно , а угол при основании равен 300. Найдите длину медианы, проведенной к боковой стороне.

4. Медианы треугольника равны 5, и . Докажите, что треугольник прямоугольный.

5. Числа , и выражают длины медиан некоторого треугольника. Докажите, что если выполняется равенство , то треугольник является прямоугольным.

Медиана, проведенная к гипотенузе

1. Медиана, проведенная к гипотенузе прямоугольного треугольника, равна 3 см и делит прямой угол в отношении 2:1. Найдите меньший катет.

2. АА1, ВВ1, СС1 – медианы треугольника АВС. . Найдите .

3. Медианы треугольника АВС АА1, ВВ1 и СС1 пересекаются в точке О. .см. см. Найдите ВО.

4. Гипотенуза прямоугольного треугольника в 4 раза больше проведенной к ней высоты. Найдите острые углы треугольника.

О т в е т: 150; 750.

5. В трапеции ABCD углы при основании AD равны 200 и 700, длина отрезка, соединяющего середины оснований, равна 3. Найдите длину отрезка, соединяющего середины диагоналей трапеции.

· , , Ленинградские математические кружки

· , Задачи по планиметрии, Издательство МЦНМО, 2001г

· интернет сайт http://zadachi. ***** Задачи по геометрии

· Всероссийская олимпиада по математике, 2008 год,

· Турнир им. Ломоносова, 2001 год

· Московская математическая регата, 2012/13 г, 8 класс