Точка равноудаленная от всех вершин треугольника является центром окружности

Видео:Точка, равноудаленная от всех вершин многоугольникаСкачать

Определение окружности, описанной около треугольника

Определение 1. Окружностью, описанной около треугольника называется окружность, проходящей через все три вершины треугольника (Рис.1).

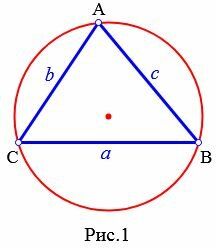При этом треугольник называется треугольником вписанным в окружность .

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Теорема об окружности, описанной около треугольника

Теорема 1. Около любого треугольника можно описать окружность.

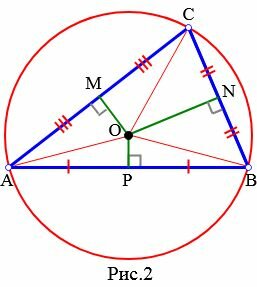Доказательство. Пусть задан произвольный треугольник ABC (Рис.2). Обозначим точкой O точку пересечения серединных перпендикуляров к его сторонам. Проведем отрезки OA, OB и OC. Поскольку точка O равноудалена от точек A, B и C, то OA=OB=OC. Тогда окружность с центром O и радиусом OA проходит через все три вершины треугольника ABC и, следовательно, является окружностью, описанной около треугольника ABC.

Из теоремы 1 следует, что центром описанной около треугольника окружности является точка пересечения серединных перпендикуляров к сторонам треугольника.

Замечание 1. Около любого треугольника можно описать только одну окружность.

Доказательство. Допустим, что около треугольника можно описать две окружности. Тогда центр каждой из этих окружностей равноудален от вершин треугольника и совпадает с точкой O пересечения серединных перпендикуляров сторон треугольника. Радиус этих окружностей равен расстоянию от точки O до вершин треугольника. Поэтому эти окружности совпадают.

Видео:Центр окружности описанной вокруг треугольникаСкачать

Точка равноудаленная от всех вершин треугольника является центром окружности

554. Докажите, что если центр окружности, описанной около треугольника, принадлежит его высоте, то этот треугольник равнобедренный.

555. Докажите, что если центр окружности, вписанной в треугольник, принадлежит его медиане, то этот треугольник равнобедренный.

556. Докажите, что если центры вписанной и описанной окружностей треугольника совпадают, то этот треугольник равносторонний.

557. Боковая сторона равнобедренного треугольника делится точкой касания вписанной окружности в отношении 7 : 5, считая от вершины треугольника. Найдите стороны треугольника, если его периметр равен 68 см.

558. Периметр треугольника ABC , описанного около окружности, равен 52 см. Точка касания со стороной AB делит эту сторону в отношении 2 : 3, считая от вершины A . Точка касания со стороной BC удалена от вершины C на 6 см. Найдите стороны треугольника.

559. В треугольник с углами 30°, 70° и 80° вписана окружность. Найдите углы треугольника, вершины которого являются точками касания вписанной окружности со сторонами данного треугольника.

560. Окружность, вписанная в равнобедренный треугольник ABC , касается его боковых сторон AB и BC в точках M и N соответственно. Докажите, что MN ‖ AC .

561. Докажите, что если центр окружности, описанной около треугольника, принадлежит его стороне, то этот треугольник — прямоугольный.

562. В треугольник ABC вписана окружность, касающаяся стороны AB в точке M , BС = a . Докажите, что AM = p — a , где p — полупериметр треугольника ABC .

563. К окружности, вписанной в равносторонний треугольник со стороной a , провели касательную, пересекающую две его стороны. Найдите периметр треугольника, который эта касательная отсекает от данного.

564. В равнобедренный треугольник ABC ( AB = BC ) с основанием 10 см вписана окружность. К этой окружности проведены три касательные, отсекающие от данного треугольника треугольники ADK , BEF и CMN . Сумма периметров этих треугольников равна 42 см. Чему равна боковая сторона данного треугольника?

565. В треугольнике ABC отрезок BD — медиана, AB = 7 см, BC = 8 см. В треугольники ABD и BDC вписали окружности. Найдите расстояние между точками касания этих окружностей с отрезком BD .

566. Каждый из углов BAC и ACB треугольника ABC разделили на три равные части (рис. 308). Докажите, что ∠ AMN = ∠ CMN .

567. Пусть вершина угла B недоступна (рис. 309). С помощью транспортира и линейки без делений постройте прямую, содержащую биссектрису угла B .

568. Точки F и O — центры вписанной и описанной окружностей равнобедренного треугольника ABC соответственно (рис. 310). Они находятся на одинаковом расстоянии от его основания AC . Найдите углы треугольника ABC .

Упражнения для повторения

569. Биссектриса угла ABC образует с его стороной угол, равный углу, смежному с углом ABC . Найдите угол ABC .

570. В равнобедренном треугольнике из вершины одного угла при основании провели высоту треугольника, а из вершины другого угла при основании — биссектрису треугольника. Один из углов, образовавшихся при пересечении проведённых биссектрисы и высоты, равен 64°. Найдите углы данного треугольника.

571. На рисунке 311 BC ‖ AD , AB = 3 см, BC = 10 см. Биссектриса угла BAD пересекает отрезок BC в точке K . Найдите отрезки BK и KC .

572. В треугольнике ABC известно, что AB = BC , AM и CK — медианы этого треугольника. Докажите, что MK ‖ AC .

Наблюдайте, рисуйте, конструируйте, фантазируйте

573. В квадрате ABCD вырезали заштрихованную фигуру (рис. 312). Разделите оставшуюся часть квадрата на четыре равные фигуры.

Видео:✓ Три окружности | Планиметрия | Олимпиада Ломоносов-2020 | Борис ТрушинСкачать

Описанная окружность

Окружность описанная около многоугольника — это окружность, на которой лежат все вершины многоугольника. Вписанный в окружность многоугольник — это многоугольник, все вершины которого лежат на окружности. На рисунке 1 четырехугольник АВСD вписан в окружность с центром О, а четырехугольник АЕСD не является вписанным в эту окружность, так как вершина Е не лежит на окружности.

Теорема

Доказательство

Дано: произвольный АВС.

Доказать: около АВС можно описать окружность.

Доказательство:

1. Проведем серединные перпендикуляры к сторонам АВС, которые пересекутся в точке О (по свойству серединных перпендикуляров треугольника). Соединим точку О с точками А, В и С (Рис. 2).

Точка О равноудалена от вершин АВС (по теореме о серединном перпендикуляре), поэтому ОА = ОВ = ОС. Следовательно, окружность с центром О радиуса ОА проходит через все три вершины треугольника, значит, является описанной около АВС. Теорема доказана.

Замечание 1

Доказательство

Предположим, что около треугольника можно описать две окружности. Тогда центр каждой из них равноудален от его вершин и поэтому совпадает с точкой О пересечения серединных перпендикуляров к сторонам треугольника, а радиус равен расстоянию от точки О до вершин треугольника. Следовательно, эти окружности совпадают, т.е. около треугольника можно описать только одну окружность. Что и требовалось доказать.

Замечание 2

Доказательство

Рассмотрим, например, ромб, не являющийся квадратом. Такой ромб можно «поместить» в окружность так, что две его вершины будут лежать на этой окружности (Рис. 3), но нельзя «поместить» ромб в окружность так, чтобы все его вершины лежали на окружности, т.к. диаметр окружности, равный одной из диагоналей ромба, будет больше (меньше) второй диагонали, т.е. нельзя описать окружность. Что и требовалось доказать.

Если же около четырехугольника можно описать окружность, то его углы обладают следующим замечательным свойством:

Доказательство

Рассмотрим четырехугольник АВСD, вписанный в окружность (Рис. 4).

Углы В и D — вписанные, тогда по теореме о вписанном угле: В = АDС, D = АВС, откуда следует В + D = АDС + АВС = (АDС + АВС). Дуги АDС и АВС вместе составляют окружность, градусная мера которой равна 360 0 , т.е. АDС + АВС = 360 0 , тогда В + D = 360 0 = 180 0 . Что и требовалось доказать.

Верно и обратное утверждение:

Доказательство

Дано: четырехугольник АВСD, BАD + BСD = 180 0 .

Доказать: около АВСD можно описать окружность.

Доказательство:

Проведем окружность через три вершины четырехугольника: А, В и D (Рис. 5), — и докажем, что она проходит также через вершину С, т.е. является описанной около четырехугольника АВСD.

Предположим, что это не так. Тогда вершина С лежит либо внутри круга, либо вне его.

Рассмотрим первый случай, когда точка С лежит внутри круга (Рис. 6).

ВСD — внешний угол СFD, следовательно, BСD = ВFD + FDE. (1)

Углы ВFD и FDE — вписанные. По теореме о вписанном угле ВFD = ВАD и FDE = ЕF, тогда, подставляя данные равенства в (1), получим: BСD = ВАD + ЕF = (ВАD + ЕF), следовательно, ВСDВАD.

BАD — вписанный, тогда по теореме о вписанном угле BАD = ВЕD, тогда BАD + BСD(ВЕD + ВАD).

Дуги ВЕD и ВАD вместе составляют окружность, градусная мера которой равна 360 0 , т.е. ВЕD + ВАD = 360 0 , тогда BАD + BСD360 0 = 180 0 .

Итак, мы получили, что BАD + BСD180 0 . Но это противоречит условию BАD + BСD =180 0 , и, значит, наше предположение ошибочно, т.е. точка С лежит на окружности, значит, около четырехугольника АВСD можно описать окружность.

Рассмотрим второй случай, когда точка С лежит вне круга (Рис. 7).

По теореме о сумме углов треугольника в ВСF: С + В + F = 180 0 , откуда С = 180 0 — ( В + F). (2)

В — вписанный, тогда по теореме о вписанном угле В = ЕF. (3)

F и ВFD — смежные, поэтому F + ВFD = 180 0 , откуда F = 180 0 — ВFD = 180 0 — ВАD. (4)

Подставим (3) и (4) в (2), получим:

С = 180 0 — (ЕF + 180 0 — ВАD) = 180 0 — ЕF — 180 0 + ВАD = (ВАD — ЕF), следовательно, СВАD.

А — вписанный, тогда по теореме о вписанном угле А = ВЕD, тогда А + С(ВЕD + ВАD). Но это противоречит условию А + С =180 0 , и, значит, наше предположение ошибочно, т.е. точка С лежит на окружности, значит, около четырехугольника АВСD можно описать окружность. Что и требовалось доказать.

Примечание:

Окружность всегда можно описать:

Поделись с друзьями в социальных сетях:

🔍 Видео

№203. Через центр О окружности, вписанной в треугольник ABC, проведена прямая ОK, перпендикулярнаяСкачать

№143. Расстояние от точки М до каждой из вершин правильного треугольника ABC равно 4 смСкачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

№199. Точка S равноудалена от вершин прямоугольного треугольника и не лежит в плоскости этогоСкачать

ГЕОМЕТРИЯ 8 класс: 4 замечательные точкиСкачать

Пирамиды, в которых высота проходит через центр описанной около основания окружностиСкачать

Три точки, задающие окружностьСкачать

#207. Окружность девяти точек | лемма о трезубце | ортотреугольник | прямая ЭйлераСкачать

Задача 3 ЕГЭ по математике. Урок 84Скачать

9 класс. Геометрия. ОГЭ. Окружность. Четырехугольники.Скачать

Геометрия 9 класс (Урок№21 - Правильный многоугольник. Описанная и вписанная окружность.)Скачать

№204. Прямая ОМ перпендикулярна к плоскости правильного треугольника ABC и проходит через центр ОСкачать

Окружность и треугольникСкачать

№200. Докажите, что любая точка прямой, которая проходит через центр окружности, описанной около мноСкачать

Вторая замечательная точка треугольникаСкачать

Построение окружности по трём точкам.Скачать