Свойство координат векторов на плоскости (5 видео)

Координаты вектора в математике

Координаты вектора ― это коэффициенты единственно возможной линейной комбинации базисных векторов в выбранной системе координат, равной данному вектору.

Содержание:

Содержание

Координаты вектора
Свойства координат вектора
Операции над векторами и их свойства: сложение и умножение
Сложение двух векторов
Сложение нескольких векторов
Умножение вектора на число
Свойства операций над векторами
Векторы в пространстве и метод координат
Система координат в пространстве
Плоскость в пространстве задается уравнением:
🎦 Видео

Видео:Векторы. Метод координат. Вебинар | МатематикаСкачать

Координаты вектора

Для введения понятия координат вектора следует рассмотреть возможность разложения вектора по осям координат. Мы хотим каждый вектор задать парой чисел — проекциями этого вектора на оси координат. При таком подходе действия над векторами можно свести к действиям с парами чисел.

Определим проекции вектора на координатную ось. Пусть задана координатная ось Ох. Единичный отрезок ОЕ теперь будем считать единичным вектором , т. е. вектором, длина которого равна 1 (рис. 2.506).

Возьмем любой вектор и отложим его от некоторой точки А:

Спроектируем точки А и В на ось Ох. Получим точки и составляющую вектора по оси Ох (рис. 2.507). Ее длина со знаком «плюс» или «минус» и называют проекцией вектора на ось Ох.

Определение. Проекцией вектора на ось Ох называют длину его составляющей по этой оси, взятую со знаком «плюс» или «минус». При этом берется знак «плюс», если направление вектора совпадает с направлением оси Ох, и знак «минус», если эти направления противоположны. Если = 0, т. е.

Проекция точки — точка, проекция отрезка — отрезок (или точка), а проекция вектора — число.

Вектор получается из коллинеарного ему единичного вектора умножением на . При этом если сонаправлен с , то Если же противоположно направлен , то

Следовательно, имеет место равенство

Можно доказать следующие свойства проекций векторов на ось.

1. Равные векторы имеют равные проекции на заданную ось.

2. При сложении векторов их проекции на ось складываются.

3. При умножении вектора на число его проекция умножается на это число.

Прежде чем ввести понятие координат вектора, докажем теорему.

Теорема 6. Пусть на плоскости введена прямоугольная система координат с единичными векторами координатных осей Ох и Оу. Пусть — некоторый вектор, а — его проекции на оси координат. Тогда вектор единственным образом представляется в виде (рис. 2.508).

Выше получена формула для разложения вектора а по векторам (с учетом обозначения): .

Пару чисел называют координатами вектора в данной системе координат.

Координаты вектора в пространстве определяются так же, как на плоскости. Справедлива следующая теорема.

Теорема 7. Пусть в пространстве введена прямоугольная система координат с единичными векторами координатных осей Ох, Оу, Oz. Тогда вектор единственным образом представляется в виде (рис. 2.509).

Числа называются координатами вектора относительно векторов, которые называются базисными векторами или, короче, базисом.

Введенные координаты вектора позволяют получить формулу длины вектора.

Рассмотрим рисунок 2.508.

1. Если точка А не лежит на координатных осях, то треугольник прямоугольный.

2. (1, теорема Пифагора).

3. Так как то получаем, что (2).

4. Но поэтому

(3, 4).

Формула справедлива и в тех случаях, когда точка А лежит на какой-то оси координат.

Свойства координат вектора

В курсе геометрии нам практически не приходится работать с векторами в координатах (это приходится делать в курсе физики). Можно доказать различные свойства координат вектора:

1. Координаты равных векторов соответственно равны. Обратно: векторы, имеющие соответственно равные координаты, равны.

2. При сложении векторов их соответствующие координаты складываются. А именно, если

3. При умножении вектора на число его координаты умножаются на это число. А именно, если

Координаты вектора связаны с координатами точки по следующему правилу: чтобы найти координаты вектора, нужно от координат конца вектора отнять координаты начала вектора.

В частности, если вектор отложен от начала координат, то координаты вектора равны координатам его конца.

Возьмем в пространстве некую прямоугольную систему координат с началом в точке О и координатными осями х, у, z (рис. 2.510). Пусть А, В, С — точки с единичными координатами на этих осях, т. е. А(1, 0, 0), В(0, 1, 0), С(0, 0, 1).

Тогда векторы — это направляющие единичные векторы координатных осей х, у, z.

Возьмем любую точку М(х, у, г), и пусть — ее радиус-вектор.

Теорема 8. Координаты точки М соответственно равны координатам ее радиус-вектора относительно базиса .

Эта лекция взята со страницы полного курса лекций по изучению предмета «Математика»:

Смотрите также дополнительные лекции по предмету «Математика»:

Видео:9 класс, 2 урок, Координаты вектораСкачать

Операции над векторами и их свойства: сложение и умножение

Прежде чем приступить к тематике статьи, напомним основные понятия.

Вектор – отрезок прямой, характеризующийся численным значением и направлением. Вектор обозначается строчной латинской буквой со стрелкой сверху. При наличии конкретных точек границ обозначение вектора выглядит как две прописные латинские буквы (маркирующие границы вектора) также со стрелкой сверху.

Нулевой вектор – любая точка плоскости, обозначается как нуль со стрелкой сверху.

Длина вектора – величина, равная или большая нуля, определяющая длину отрезка, составляющего вектор.

Коллинеарные векторы – лежащие на одной прямой или на параллельных прямых. Не выполняющие это условие векторы называют неколлинеарными.

Видео:Координаты вектора. 9 класс.Скачать

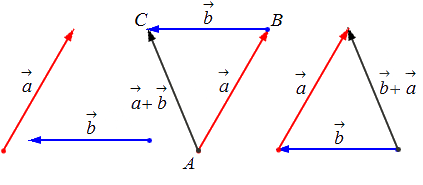
Сложение двух векторов

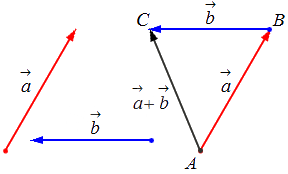
Исходные данные: векторы a → и b → . Для выполнения над ними операции сложения необходимо из произвольной точки отложить вектор A B → , равный вектору а → ; из полученной точки undefined – вектор В С → , равный вектору b → . Соединив точки undefined и C , получаем отрезок (вектор) А С → , который и будет являться суммой исходных данных. Иначе описанную схему сложения векторов называют правилом треугольника.

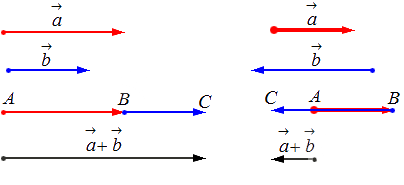
Геометрически сложение векторов выглядит так:

— для неколлинеарных векторов:

— для коллинеарных (сонаправленных или противоположнонаправленных) векторов:

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

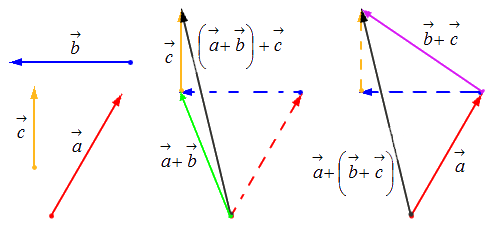
Сложение нескольких векторов

Взяв за основу описанную выше схему, мы получаем возможность произвести операцию сложения векторов в количестве более 2: поочередно прибавляя каждый последующий вектор.

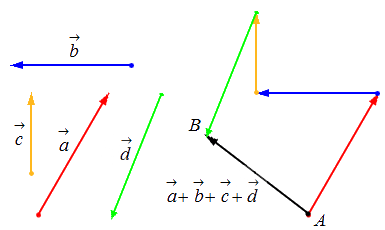
Исходные данные: векторы a → , b → , c → , d → . Из произвольной точки А на плоскости необходимо отложить отрезок (вектор), равный вектору a → ; затем от конца полученного вектора откладывается вектор, равный вектору b → ; далее – по тому же принципу откладываются последующие векторы. Конечной точкой последнего отложенного вектора будет точка B , а полученный отрезок (вектор) A B → – суммой всех исходных данных. Описанную схему сложения нескольких векторов называют также правилом многоугольника .

Геометрически оно выглядит следующим образом:

Отдельной схемы действия по вычитанию векторов нет, т.к. по сути разность векторов a → и b → есть сумма векторов a → и — b → .

Видео:Координаты вектора в пространстве. 11 класс.Скачать

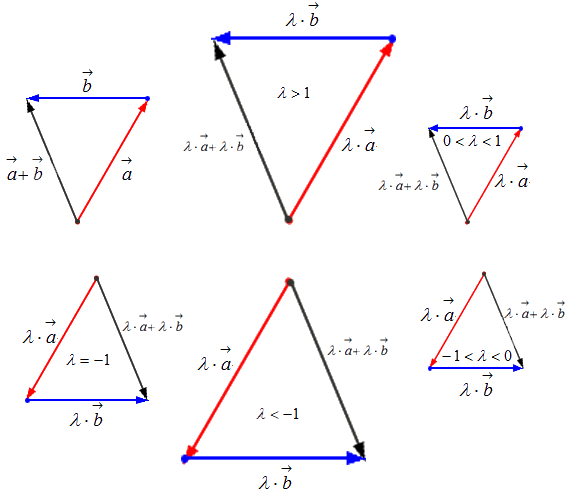
Умножение вектора на число

Чтобы произвести действие умножения вектора на некое число k , необходимо учитывать следующие правила:
— если k > 1 , то это число приведет к растяжению вектора в k раз;
— если 0 k 1 , то это число приведет к сжатию вектора в 1 k раз;
— если k 0 , то это число приведет к смене направления вектора при одновременном выполнении одного из первых двух правил;
— если k = 1 , то вектор остается прежним;
— если одно из множителей – нулевой вектор или число, равное нулю, результатом умножения будет нулевой вектор.

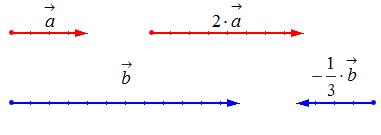
Исходные данные:
1) вектор a → и число k = 2 ;
2) вектор b → и число k = — 1 3 .

Геометрически результат умножения в соответствии с указанными выше правилами будет выглядеть следующим образом:

Видео:Координаты точки и координаты вектора 1.Скачать

Свойства операций над векторами

Описанным выше операциям над векторами присущи свойства, некоторые из которых очевидны, а прочие можно обосновать геометрически.

Исходные данные: векторы a → , b → , c → и произвольные действительные числа λ и μ .

Свойство коммутативности: a ⇀ + b → = b → + a → .
Свойство ассоциативности: ( a → + b → ) + c → = a → + ( b → + c → ) .
Свойство использования нейтрального элемента по сложению (нулевой вектор 0 → ⃗). Это очевидное свойство: a → + 0 → = a →
Свойство использования нейтрального элемента по умножению (число, равное единице): 1 · a → = a → . Это очевидное свойство, не предполагающее никаких геометрических преобразований.
Любой ненулевой вектор a → имеет противоположный вектор — a → и верным является равенство: a → + ( — a → ) = 0 → . Указанное свойство — очевидное.
Сочетательное свойство операции умножения: ( λ · µ ) · a → = λ · ( µ · a → ) . Например, растяжение вектора при умножении на число 10 можно произвести, сначала растянув вектор в 2 раза, а затем полученный результат еще в 5 раз. Также возможен вариант умножения на число 10 при сжатии вектора в 5 раз и последующего растяжения полученного результата в 50 раз.
Первое распределительное свойство (очевидно): ( λ + µ ) · a → = λ · a → + µ · a → .
Второе распределительное свойство: λ · ( a → + b → ) = λ · a → + λ · b → .
Геометрически это свойство определяется подобием треугольников:

Свойства коммутативности и ассоциативности дают возможность складывать векторы в произвольном порядке.

Перечисленные свойства операций позволяют осуществлять необходимые преобразования векторно-числовых выражений аналогично привычным числовым. Рассмотрим это на примере.

Задача: упростить выражение a → — 2 · ( b → + 3 · a → )
Решение
— используя второе распределительное свойство, получим: a → — 2 · ( b → + 3 · a → ) = a → — 2 · b → — 2 · ( 3 · a → )
— задействуем сочетательное свойство умножения, выражение приобретет следующий вид: a → — 2 · b → — 2 · ( 3 · a → ) = a → — 2 · b → — ( 2 · 3 ) · a → = a → — 2 · b → — 6 · a →
— используя свойство коммутативности, меняем местами слагаемые: a → — 2 · b → — 6 · a → = a → — 6 · a → — 2 · b →
— затем по первому распределительному свойству получаем: a → — 6 · a → — 2 · b → = ( 1 — 6 ) · a → — 2 · b → = — 5 · a → — 2 · b → Краткая запись решения будет выглядеть так: a → — 2 · ( b → + 3 · a → ) = a → — 2 · b → — 2 · 3 · a → = 5 · a → — 2 · b →
Ответ: a → — 2 · ( b → + 3 · a → ) = — 5 · a → — 2 · b →

Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Векторы в пространстве и метод координат

Существует два способа решения задач по стереометрии

Первый — классический — требует отличного знания аксиом и теорем стереометрии, логики, умения построить чертеж и свести объемную задачу к планиметрической. Способ хорош тем, что развивает мозги и пространственное воображение.

Другой метод — применение векторов и координат. Это простые формулы, алгоритмы и правила. Он очень удобен, особенно когда времени до экзамена мало, а решить задачу хочется.

Если вы освоили векторы на плоскости и действия с ними — то и с векторами в пространстве разберетесь. Многие понятия окажутся знакомыми.

Видео:Векторы и действия над ними, проекция вектора на координатные оси. 9 класс.Скачать

Система координат в пространстве

Выберем начало координат. Проведем три взаимно перпендикулярные оси X, Y и Z. Зададим удобный масштаб.

Получилась система координат в трехмерном пространстве. Теперь каждая его точка характеризуется тремя числами — координатами по X, Y и Z. Например, запись M(−1; 3; 2) означает, что координата точки M по X (абсцисса) равна −1, координата по Y (ордината) равна 3, а координата по Z (аппликата) равна 2.

Векторы в пространстве определяются так же, как и на плоскости. Это направленные отрезки, имеющие начало и конец. Только в пространстве вектор задается тремя координатами x, y и z:

Как найти координаты вектора? Как и на плоскости — из координаты конца вычитаем координату начала.

Длина вектора в пространстве – это расстояние между точками A и B. Находится как корень квадратный из суммы квадратов координат вектора.

Пусть точка M – середина отрезка AB. Ее координаты находятся по формуле:

Для сложения векторов применяем уже знакомые правило треугольника и правило параллелограмма

Сумма векторов, их разность, произведение вектора на число и скалярное произведение векторов определяются так же, как и на плоскости. Только координат не две, а три. Возьмем векторы и .

Произведение вектора на число:

Скалярное произведение векторов:

Косинус угла между векторами:

Последняя формула удобна для нахождения угла между прямыми в пространстве. Особенно если эти прямые – скрещиваются. Напомним, что так называются прямые, которые не параллельны и не пересекаются. Они лежат в параллельных плоскостях.

1. В кубе ABCDA₁B₁C₁D₁ точки E и K — середины ребер соответственно A₁B₁ и B₁C₁. Найдите косинус угла между прямыми AE и BK.

Если вам достался куб — значит, повезло. Он отлично вписывается в прямоугольную систему координат. Строим чертеж:

Длина ребра куба не дана. Какой бы она ни была, угол между AE и BK от нее не зависит. Поэтому возьмем единичный куб, все ребра которого равны 1.

Прямые AE и BK — скрещиваются. Найдем угол между векторами и . Для этого нужны их координаты.

Запишем координаты векторов:

и найдем косинус угла между векторами и :

2. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, точки E, K — середины ребер SB и SC соответственно. Найдите косинус угла между прямыми AE и BK.

Лучше всего выбрать начало координат в центре основания пирамиды, а оси X и Y сделать параллельными сторонам основания.

Координаты точек A, B и C найти легко:

Из прямоугольного треугольника AOS найдем

Координаты вершины пирамиды:

Точка E — середина SB, а K — середина SC. Воспользуемся формулой для координат середины отрезка и найдем координаты точек E и K.

Найдем координаты векторов и

и угол между ними:

Покажем теперь, как вписать систему координат в треугольную призму:

3. В правильной треугольной призме ABCA₁B₁C₁, все ребра которой равны 1, точка D — середина ребра A₁B₁. Найдите косинус угла между прямыми AD и BC₁

Пусть точка A — начало координат. Возьмем ось X параллельно стороне BC, а ось Y перпендикулярно ей. Другими словами, на оси Y будет лежать отрезок AH, являющийся высотой треугольника ABC. Нарисуем отдельно нижнее основание призмы.

Запишем координаты точек:

Точка D — середина A₁B₁. Значит, пользуемся формулами для координат середины
отрезка.

Найдем координаты векторов и , а затем угол между ними:

Смотрите, как легко с помощью векторов и координат найти угол между прямыми. А если требуется найти угол между плоскостями или между прямой и плоскостью? Для решения подобных задач нам понадобится уравнение плоскости в пространстве.

Видео:Координаты вектора. Векторы на координатной плоскости. Геометрия 8-9 классСкачать

Плоскость в пространстве задается уравнением:

Здесь числа A, B и C — координаты вектора, перпендикулярного этой плоскости. Его называют нормалью к плоскости.

Вместо x, y и z можно подставить в уравнение координаты любой точки, принадлежащей данной плоскости. Получится верное равенство.

Плоскость в пространстве можно провести через любые три точки, не лежащие на одной прямой. Поэтому для того, чтобы написать уравнение плоскости, берем координаты трех принадлежащих ей точек. Подставляем их по очереди в уравнение плоскости. Решаем полученную систему.

Покажем, как это делается.

Напишем уравнение плоскости, проходящей через точки M (1; 0; 1), N (2; −2; 0) и K (4; 1; 2).

Уравнение плоскости выглядит так:

Подставим в него по очереди координаты точек M, N и K.

То есть A + C + D = 0.

Аналогично для точки K:

Получили систему из трех уравнений:

В ней четыре неизвестных: A, B, C и D. Поэтому одну из них мы выберем сами, а другие выразим через нее. Правило простое — вместо одной из переменных можно взять любое число, не равное нулю.

Пусть, например, D = −2. Тогда:

Выразим C и B через A и подставим в третье уравнение:

Решив систему, получим:

Уравнение плоскости MNK имеет вид:

Умножим обе части уравнения на −3. Тогда коэффициенты станут целыми:

Вектор — это нормаль к плоскости MNK.

Уравнение плоскости, проходящей через заданную точку имеет вид:

Угол между плоскостями равен углу между нормалями к этим плоскостям:

Не правда ли, знакомая формула? Скалярное произведение нормалей поделили на произведение их длин.

Заметим, что при пересечении двух плоскостей вообще-то образуется четыре угла.

Мы берем меньший из них. Поэтому в формуле стоит модуль скалярного произведения — чтобы косинус угла был неотрицателен.

4. В кубе ABCDA₁B₁C₁D₁ точки E и F — середины ребер соответственно A₁B₁ и A₁D₁. Найдите тангенс угла между плоскостями AEF и BDD₁.

Строим чертеж. Видно, что плоскости AEF и BDD₁ пересекаются где-то вне куба. В классическом решении пришлось бы строить линию их пересечения. Но векторно-координатный метод значительно всё упрощает. Не будем ломать голову над тем, по какой прямой пересекаются плоскости. Просто отметим координаты нужных нам точек и найдем угол между нормалями к плоскостям AEF и BDD₁.

Сначала — нормаль к плоскости BDD₁. Конечно, мы можем подставить координаты точек B, D и D₁ в уравнение плоскости и найти коэффициенты, которые и будут координатами вектора нормали. А можем сделать хитрее — увидеть нужную нормаль прямо на чертеже. Ведь плоскость BDD₁ — это диагональное сечение куба. Вектор перпендикулярен этой плоскости.

Итак, первый вектор нормали у нас уже есть:

Напишем уравнение плоскости AEF.

Берем уравнение плоскости и по очереди подставляем в него, вместо x, y и z, соответствующие координаты точек A, E и F.

Пусть С = -1. Тогда A = B = 2.

Уравнение плоскости AEF:

Нормаль к плоскости AEF:

Найдем угол между плоскостями:

5. Основание прямой четырехугольной призмы BCDA₁B₁C₁D₁ — прямоугольник ABCD, в котором AB = 5, AD = √33. Найдите тангенс угла между плоскостью грани AA₁D₁D и плоскостью, проходящей через середину ребра CD перпендикулярно прямой B₁D, если расстояние между прямыми A₁C₁ и BD равно √3.

Эта задача наглядно показывает, насколько векторный метод проще классического. Попробуйте, для разнообразия, построить необходимые сечения и провести все доказательства — как это делается в «классике» 🙂

Строим чертеж. Прямую четырехугольную призму можно по-другому назвать «параллелепипед».

Замечаем, что длина и ширина параллелепипеда у нас есть, а вот высота — вроде не дана. Как же ее найти?

«Расстояние между прямыми A₁C₁ и BD равно √3». Прямые A₁C₁ и BD скрещиваются. Одна из них — диагональ верхнего основания, другая — диагональ нижнего. Вспомним, что расстояние между скрещивающимися прямыми равно длине их общего перпендикуляра. Общий перпендикуляр к A₁C₁ и BD — это, очевидно, OO₁, где O — точка пересечения диагоналей нижнего основания, O₁ — точка пересечения диагоналей верхнего. А отрезок OO₁ и равен высоте параллелепипеда.

Плоскость AA₁ D₁ D — это задняя грань призмы на нашем чертеже. Нормаль к ней — это любой вектор, перпендикулярный задней грани, например, вектор или, еще проще, вектор .

Осталась еще «плоскость, проходящая через середину ребра CD перпендикулярно прямой B₁D». Но позвольте, если плоскость перпендикулярна прямой B₁D — значит, B₁D и есть нормаль к этой плоскости! Координаты точек B₁ и D известны:

Координаты вектора — тоже:

Находим угол между плоскостями, равный углу между нормалями к ним:

Зная косинус угла, находим его тангенс по формуле

Получим:

Ответ:

Угол между прямой m и плоскостью α тоже вычисляется с помощью скалярного произведения векторов.

Пусть — вектор, лежащий на прямой m (или параллельный ей), — нормаль к плоскости α.

Находим синус угла между прямой m и плоскостью α по формуле:

6. В кубе ABCDA₁B₁C₁D₁ точка E — середина ребра A₁B₁. Найдите синус угла между прямой AE и плоскостью BDD₁.

Как всегда, рисуем чертеж и выбираем систему координат

Находим координаты вектора .

Нужно ли нам уравнение плоскости BDD₁? В общем-то, без него можно обойтись. Ведь эта плоскость является диагональным сечением куба, а значит, нормалью к ней будет любой вектор, ей перпендикулярный. Например, вектор .

Найдем угол между прямой и плоскостью:

Ответ:

Расстояние от точки M с координатами x₀, y₀ и z₀ до плоскости α, заданной уравнением Ax + By + Cz + D = 0, можно найти по формуле:

7. В основании прямоугольного параллелепипеда BCDA₁B₁C₁D₁ лежит прямоугольник ABCD со сторонами AB = , AD = . Высота параллелепипеда AA₁ = . Найдите расстояние от точки A до плоскости A₁DB.

Построим чертеж и выпишем координаты точек:

Запишем уравнение плоскости A₁DB. Вы помните, как это делается — по очереди подставляем координаты точек A₁, D и B в уравнение A_x + B_e + C_z + D

Решим эту систему. Выберем

Тогда

Уравнение плоскости A₁DB имеет вид:

Дальше все просто. Находим расстояние от точки A до плоскости A₁DB:

В некоторых задачах по стереометрии требуется найти расстояние от прямой до параллельной ей плоскости. В этом случае можно выбрать любую точку, принадлежащую данной прямой.