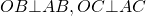Свойство двух касательных к окружности проведенных из одной точки

Рассмотрим, какими свойствами обладают отрезки касательных к окружности, проведенные из одной точки.

(Свойство касательных, проведенных из одной точки)

Отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.

AB=AC ∠BAO=∠CAO

Дано: окружность (O;R),

AB и AC — касательные к окружности (O;R),

B, C — точки касания.

Доказать: AB=AC, ∠BAO=∠CAO.

Следовательно, треугольники ABO и ACO — прямоугольные. У них

1) катеты OB=OC (как радиусы)

2) гипотенуза OA — общая сторона.

Из равенства треугольников следует равенство соответствующих сторон:

Видео:Вариант 77, № 7. Свойство касательной. Теорема о касательных, проведенных из одной точки. Задача 1Скачать

Касательная к окружности

О чем эта статья:

Видео:Отрезки касательных из одной точки до точек касания окружности равны | Окружность | ГеометрияСкачать

Касательная к окружности, секущая и хорда — в чем разница

В самом названии касательной отражается суть понятия — это прямая, которая не пересекает окружность, а лишь касается ее в одной точке. Взглянув на рисунок окружности ниже, несложно догадаться, что точку касания от центра отделяет расстояние, в точности равное радиусу.

Касательная к окружности — это прямая, имеющая с ней всего одну общую точку.

Если мы проведем прямую поближе к центру окружности — так, чтобы расстояние до него было меньше радиуса — неизбежно получится две точки пересечения. Такая прямая называется секущей, а отрезок, расположенный между точками пересечения, будет хордой (на рисунке ниже это ВС ).

Секущая к окружности — это прямая, которая пересекает ее в двух местах, т. е. имеет с ней две общие точки. Часть секущей, расположенная внутри окружности, будет называться хордой.

Видео:Свойство секущей и касательной, проведённых из одной точки.Скачать

Свойства касательной к окружности

Выделяют четыре свойства касательной, которые необходимо знать для решения задач. Два из них достаточно просты и легко доказуемы, а вот еще над двумя придется немного подумать. Рассмотрим все по порядку.

Касательная к окружности и радиус, проведенный в точку касания, взаимно перпендикулярны.

Не будем принимать это на веру, попробуем доказать. Итак, у нас даны:

• окружность с центральной точкой А;
• прямая а — касательная к ней;
• радиус АВ, проведенный к касательной.

Докажем, что касательная и радиус АВ взаимно перпендикулярны, т.е. а ⟂ АВ.

Пойдем от противного — предположим, что между прямой а и радиусом АВ нет прямого угла и проведем настоящий перпендикуляр к касательной, назвав его АС.

В таком случае наш радиус АВ будет считаться наклонной, а наклонная, как известно, всегда длиннее перпендикуляра. Получается, что АВ > АС. Но если бы это было на самом деле так, наша прямая а пересекалась бы с окружностью два раза, ведь расстояние от центра А до нее — меньше радиуса. Но по условию задачи а — это касательная, а значит, она может иметь лишь одну точку касания.

Итак, мы получили противоречие. Делаем вывод, что настоящим перпендикуляром к прямой а будет вовсе не АС, а АВ.

Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.

Задача

У нас есть окружность, центр которой обозначен О. Из точки С проведена прямая, и она касается этой окружности в точке А. Известно, что ∠АСО = 28°. Найдите величину дуги АВ.

Мы знаем, что касательная АС ⟂ АО, следовательно ∠САО = 90°.

Поскольку нам известны величины двух углов треугольника ОАС, не составит труда найти величину и третьего угла.

∠АОС = 180° — ∠САО — ∠АСО = 180° — 90° — 28° = 62°

Поскольку вершина угла АОС лежит в центре окружности, можно вспомнить свойство центрального угла — как известно, он равен дуге, на которую опирается. Следовательно, АВ = 62°.

Если провести две касательных к окружности из одной точки, лежащей вне этой окружности, то их отрезки от этой начальной точки до точки касания будут равны.

Докажем и это свойство на примере. Итак, у нас есть окружность с центром А, давайте проведем к ней две касательные из точки D. Обозначим эти прямые как ВD и CD . А теперь выясним, на самом ли деле BD = CD.

Для начала дополним наш рисунок, проведем еще одну прямую из точки D в центр окружности. Как видите, у нас получилось два треугольника: ABD и ACD . Поскольку мы уже знаем, что касательная и радиус к ней перпендикулярны, углы ABD и ACD должны быть равны 90°.

Итак, у нас есть два прямоугольных треугольника с общей гипотенузой AD. Учитывая, что радиусы окружности всегда равны, мы понимаем, что катеты AB и AC у этих треугольников тоже одинаковой длины. Следовательно, ΔABD = ΔACD (по катету и гипотенузе).. Значит, оставшиеся катеты, а это как раз наши BD и CD (отрезки касательных к окружности), аналогично равны.

Важно: прямая, проложенная из стартовой точки до центра окружности (в нашем примере это AD), делит угол между касательными пополам.

Задача 1

У нас есть окружность с радиусом 4,5 см. К ней из точки D, удаленной от центра на 9 см, провели две прямые, которые касаются окружности в точках B и C. Определите градусную меру угла, под которым пересекаются касательные.

Решение

Для этой задачи вполне подойдет уже рассмотренный выше рисунок окружности с радиусами АВ и АC. Поскольку касательная ВD перпендикулярна радиусу АВ , у нас есть прямоугольный треугольник АВD. Зная длину его катета и гипотенузы, определим величину ∠BDA.

∠BDA = 30° (по свойству прямоугольного треугольника: угол, лежащий напротив катета, равного половине гипотенузы, составляет 30°).

Мы знаем, что прямая, проведенная из точки до центра окружности, делит угол между касательными, проведенными из этой же точки, пополам. Другими словами:

∠BDC = ∠BDA × 2 = 30° × 2 = 60°

Итак, угол между касательными составляет 60°.

Задача 2

К окружности с центром О провели две касательные КМ и КN. Известно, что ∠МКN равен 50°. Требуется определить величину угла ∠NМК.

Решение

Согласно вышеуказанному свойству мы знаем, что КМ = КN. Следовательно, треугольник МNК является равнобедренным.

Углы при его основании будут равны, т.е. ∠МNК = ∠NМК.

∠МNК = (180° — ∠МКN) : 2 = (180° — 50°) : 2 = 65°

Соотношение между касательной и секущей: если они проведены к окружности из одной точки, лежащей вне окружности, то квадрат расстояния до точки касания равен произведению длины всей секущей на ее внешнюю часть.

Данное свойство намного сложнее предыдущих, и его лучше записать в виде уравнения.

Начертим окружность и проведем из точки А за ее пределами касательную и секущую. Точку касания обозначим В, а точки пересечения — С и D. Тогда CD будет хордой, а отрезок AC — внешней частью секущей.

Задача 1

Из точки М к окружности проведены две прямые, пусть одна из них будет касательной МA, а вторая — секущей МB. Известно, что хорда ВС = 12 см, а длина всей секущей МB составляет 16 см. Найдите длину касательной к окружности МA.

Решение

Исходя из соотношения касательной и секущей МА 2 = МВ × МС.

Найдем длину внешней части секущей:

МС = МВ — ВС = 16 — 12 = 4 (см)

МА 2 = МВ × МС = 16 х 4 = 64

Задача 2

Дана окружность с радиусом 6 см. Из некой точки М к ней проведены две прямые — касательная МA и секущая МB . Известно, что прямая МB пересекает центр окружности O. При этом МB в 2 раза длиннее касательной МA . Требуется определить длину отрезка МO.

Решение

Допустим, что МО = у, а радиус окружности обозначим как R.

В таком случае МВ = у + R, а МС = у – R.

Поскольку МВ = 2 МА, значит:

МА = МВ : 2 = (у + R) : 2

Согласно теореме о касательной и секущей, МА 2 = МВ × МС.

(у + R) 2 : 4 = (у + R) × (у — R)

Сократим уравнение на (у + R), так как эта величина не равна нулю, и получим:

Поскольку R = 6, у = 5R : 3 = 30 : 3 = 10 (см).

Ответ: MO = 10 см.

Угол между хордой и касательной, проходящей через конец хорды, равен половине дуги, расположенной между ними.

Это свойство тоже стоит проиллюстрировать на примере: допустим, у нас есть касательная к окружности, точка касания В и проведенная из нее хорда AВ. Отметим на касательной прямой точку C, чтобы получился угол AВC.

Задача 1

Угол АВС между хордой АВ и касательной ВС составляет 32°. Найдите градусную величину дуги между касательной и хордой.

Решение

Согласно свойствам угла между касательной и хордой, ∠АВС = ½ АВ.

АВ = ∠АВС × 2 = 32° × 2 = 64°

Задача 2

У нас есть окружность с центром О, к которой идет прямая, касаясь окружности в точке K. Из этой точки проводим хорду KM, и она образует с касательной угол MKB, равный 84°. Давайте найдем величину угла ОMK.

Решение

Поскольку ∠МКВ равен половине дуги между KM и КВ, следовательно:

КМ = 2 ∠МКВ = 2 х 84° = 168°

Обратите внимание, что ОМ и ОK по сути являются радиусами, а значит, ОМ = ОК. Из этого следует, что треугольник ОMK равнобедренный.

∠ОКМ = ∠ОМК = (180° — ∠КОМ) : 2

Так как центральный угол окружности равен угловой величине дуги, на которую он опирается, то:

∠ОМК = (180° — ∠КОМ) : 2 = (180° — 168°) : 2 = 6°

Видео:8 класс, 32 урок, Касательная к окружностиСкачать

Свойство двух касательных к окружности проведенных из одной точки

§3. Свойства касательных, хорд, секущих. Вписанные и описанные четырёхугольники

Рис. 17

Если из точки к окружности проведены две касательные, то длины отрезков от этой точки до точек касания равны и прямая, проходящая через центр окружности и эту точку, делит угол между касательными пополам (рис. 17).

Используя это свойство, легко решить следующую задачу.

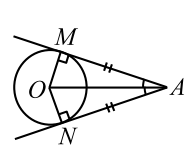
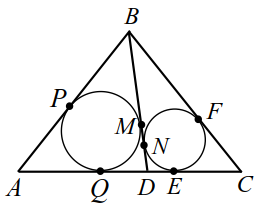
На основании $$ AC$$ равнобедренного треугольника $$ ABC$$ расположена точка $$ D$$ так, что $$ AD=a,CD=b$$. Окружности, вписанные в треугольники $$ ABD$$ и $$ DBC$$, касаются прямой $$ BD$$ в точках $$ M$$ и $$ N$$ соответственно. Найти отрезок $$ MN$$.

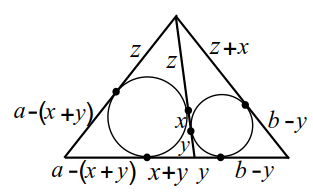Рис. 18	Рис. 18a

$$ DE=y$$, $$ QD=x+y$$, $$ AQ=AP=a-(x+y)$$, $$ EC=CF=b-y$$, $$ PB=BM=z, BF=BN=z+x$$ (рис. 18а). Выразим боковые стороны:

$$ AB=z+a-x-y$$, $$ BC=z+x+b-y$$. По условию $$ AB=BC$$; получим

Четырёхугольник называется описанным около окружности, если окружность касается всех его сторон.

В выпуклый четырёхугольник можно вписать окружность тогда и только тогда, когда суммы длин противолежащих сторон равны.

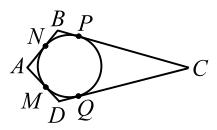Рис. 19

Пусть четырёхугольник $$ ABCD$$ описан около окружности (рис. 19).

По свойству касательных: $$ AM=AN$$, $$ NB=BP$$, $$ PC=CQ$$ и $$ QD=DM$$, поэтому

$$ AM+MD+BP+PC=AN+NB+CQ+QD$$, что означает

Докажем обратное утверждение. Пусть в выпуклом четырёхугольнике $$ ABCD$$ стороны удовлетворяют условию $$ AB+CD=BC+AD.$$ Положим $$ AD=a, AB=b, BC=c, CD=d.$$

По условию $$ a+c=b+d,$$ что равносильно $$ c-b=d-a.$$

Пусть $$ d>a.$$ Отложим на большей стороне $$ CD$$ меньшую сторону `DM=a` (рис. 20). Так как в этом случае $$ c>b$$, то также отложим $$ BN=b$$, получим три равнобедренных треугольника `ABN`, `ADM` и `MCN`.

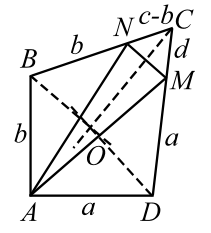Рис. 20

В равнобедренном треугольнике биссектриса угла при вершине является медианой и высотой, отсюда следует, что если провести биссектрисы углов `B`, `C` и `D`, то они разделят пополам соответственно отрезки `AN`, `MN` и `AM` и будут им перпендикулярны. Это означает, что биссектрисы будут серединными перпендикулярами трёх сторон треугольника $$ ANM$$, а они по теореме пересекаются в одной точке. Обозначим эту точку $$ O$$. Эта точка одинаково удалена от отрезков `AB` и `BC` (лежит на $$ OB$$), `BC` и `CD` (лежит на $$ OC$$) и `CD` и `AD` (лежит на $$ OD$$), следовательно, точка $$ O$$ одинакова удалена от всех четырёх сторон четырёхугольника $$ ABCD$$ и является центром вписанной окружности. Случай $$ d=a$$, как более простой, рассмотрите самостоятельно.

Равнобокая трапеция описана около окружности. Найти радиус окружности, если длины оснований равны $$ a$$ и $$ b$$.

Рис. 21

Пусть в равнобокой трапеции $$ ABCD$$ `BC=b`, `AD=a` (рис. 21). Эта трапеция равнобокая $$ (AB=CD)$$, она описана около окружности, следовательно, $$ AB+CD=AD+BC$$ Отсюда получаем:

Проведём $$ BM$$ и $$ CN$$ перпендикулярно $$ AD$$. Трапеция равнобокая, углы при основании равны, следовательно, равны и треугольники $$ ABM$$ и $$ DCN$$ и $$ AM=ND$$. По построению $$ MBCN$$ — прямоугольник, $$ MN=BC=b$$ поэтому $$ AM=<displaystyle frac>(AD-BC)-<displaystyle frac>(a-b)$$. Из прямоугольного треугольника $$ ABM$$ находим высоту трапеции $$ ABCD$$:

Очевидно, что высота трапеции равна диаметру окружности, поэтому

радиус вписанной окружности равен $$ overline<)r=<displaystyle frac>sqrt>$$.

Очень полезная задача. Заметим, что из решения также следует, что в равнобокой описанной трапеции $$ overline<)mathrmalpha =<displaystyle frac>>$$.

Градусная мера угла, образованного хордой и касательной, имеющими общую точку на окружности, равна половине градусной меры дуги, заключённой между его сторонами (рис. 22).

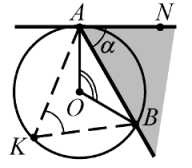Рис. 22

Рассматриваем угол $$ NAB$$ между касательной $$ NA$$ и хордой $$ AB$$. Если $$ O$$ — центр окружности, то $$ OAperp AN$$, `/_OAB=/_OBA=90^@alpha`. Сумма углов треугольника равна `180^@`, следовательно, $$ angle AOB=2alpha $$. Итак, $$ alpha =angle NAB=<displaystyle frac>angle AOB.$$

Обратим внимание, что угол $$ NAB$$ равен любому вписанному углу $$ AKB$$, опирающемуся на ту же дугу $$ AB$$.

Случай `/_alpha>=90^@` рассматривается аналогично.

Из этого свойства следует важная теорема «о касательной и секущей», которая часто используется при решении задач.

Пусть к окружности проведены из одной точки касательная $$ MA$$ и секущая $$ MB$$, пересекающая окружность в точке $$ C$$ (рис. 23). Тогда справедливо равенство

т. е. если из точки `M` к окружности проведены касательная и секущая, то квадрат отрезка касательной от точки `M` до точки касания равен произведению длин отрезков секущей от точки `M` до точек её пересечения с окружностью.

Угол $$ MAC$$ образован хордой и касательной, $$ angle MAC=angle ABC$$. Так как в треугольниках $$ MAC$$ и $$ MBA$$ угол $$ M$$ общий, то по двум углам они подобны. Из подобия следует:

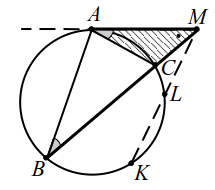Рис. 23

Если из точки $$ M$$ к окружности проведены две секущие: $$ MB$$, пересекающая окружность в точке $$ C$$ и $$ MK$$, пересекающая окружность в точке $$ L$$ (рис. 23), то справедливо равенство $$ MB·MC=MK·ML$$.

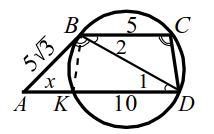Рис. 24

Окружность проходит через вершины $$ C u D$$ трапеции $$ ABCD,$$ касается боковой стороны $$ AB$$ в точке $$ B$$ и пересекает большее основание $$ AD$$ в точке $$ K$$ (рис. 24). Известно, что $$ AB=5sqrt$$, $$ BC=5$$ и $$ KD=10$$.

Найти радиус окружности.

1. Пусть $$ AK=x$$ тогда $$ AD=10+x$$ю

По теореме о касательной и секущей:

$$ A^=AK·KD$$ т. е. $$ 75=x(x+10)$$, откуда $$ x=5$$. Итак $$ AD=15$$.

2. Заметим теперь, что угол $$ ABD$$ между касательной $$ AB$$ и хордой $$ BD$$ равен вписанному углу $$ BCD$$, а из параллельности прямых $$ AD$$ и $$ BC$$ следует равенство углов `1` и `2`. По первому признаку подобия $$ △ABDsim △DCB$$. Из подобия имеем $$ <displaystyle frac>=<displaystyle frac><displaystyle frac>$$. Из последнего равенства находим, что $$ B^=AD·BC$$, т. е. $$ BD=sqrt=5sqrt$$, а из первого равенства находим $$ CD=<displaystyle frac>=5$$.

3. Так как $$ KB=CD$$ ($$ KBCD$$ — вписанная трапеция, она равнобокая), и $$ K^+B^=K^,$$ то `/_ KBD=90^@` и $$ KD$$ — диаметр окружности.

Значит, её радиус равен `5`.

Около четырёхугольника можно описать окружность тогда и только тогда, когда сумма противолежащих углов равна `180^@`.

Из этой теоремы следует:

a) из всех параллелограммов только около прямоугольника можно описать окружность;

б) около трапеции можно описать окружность только тогда, когда она равнобокая.

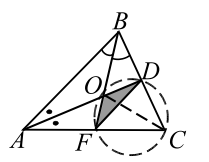Рис. 25

В треугольнике $$ ABC$$ биссектрисы $$ AD$$ и $$ BF$$ пересекаются в точке $$ O$$ (рис. 25). Известно, что точки $$ F, O, D$$, и `C` лежат на одной окружности и что $$ DF=sqrt.$$ Найти площадь треугольника $$ ODF$$.

Четырёхугольник $$ DOFC$$ вписан в окружность, по теореме 9:

$$ angle DOF=pi -angle C$$, т. е. $$ pi -<displaystyle frac>(angle A+angle B)=pi -angle C$$, откуда, учитывая, что $$ angle A+angle B+angle C=pi $$, находим $$ angle С=<displaystyle frac>$$.

Теперь заметим, что $$ O$$ — точка точка пересечения биссектрис, $$ CO$$ — биссектриса угла $$ C,$$ следовательно, углы $$ OCD$$ и $$ OCF$$ равны друг другу. Это вписанные углы, поэтому вписанные углы $$ ODF$$ и $$ OFD$$ равны им и равны друг другу. Таким образом,

Треугольник $$ DOF$$ равнобедренный с основанием $$ DF=sqrt$$ и углом при основании `30^@`. Находим его высоту, опущенную из вершины $$ O$$ и площадь треугольника $$ ODF: S=<displaystyle frac>h·DF=<displaystyle frac<sqrt>>$$.

📹 Видео

Теорема о касательной и секущей, проведенных из одной точкиСкачать

Секущая и касательная. 9 класс.Скачать

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Теорема о касательной и секущей, проведенных из одной точки. ДоказательствоСкачать

Теорема о секущей и касательной, о секущих, о пересекающихся хордах | Теоремы об окружностях - 1Скачать

#59. Олимпиадная задача о касательной к окружности!Скачать

Свойства касательной к окружности - 2Скачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

Касательные к окружности пересекаются в точке. Теорема и решение задач. Геометрия 7-8 классСкачать

Видеоурок. Решения задач по геометрии. Касательная к окружности.Скачать

Пойми Этот Урок Геометрии и получай 5-ки — Касательная и ОкружностьСкачать

Построение касательной к окружностиСкачать

Урок по теме КАСАТЕЛЬНАЯ К ОКРУЖНОСТИСкачать

Свойства касательныхСкачать

Геометрия 8 класс (Урок№28 - Свойства хорд окружности.)Скачать

Окружность, касательная, секущая и хорда | МатематикаСкачать