Найдите длину разности векторов a и b изображенных

Геометрия | 5 — 9 классы

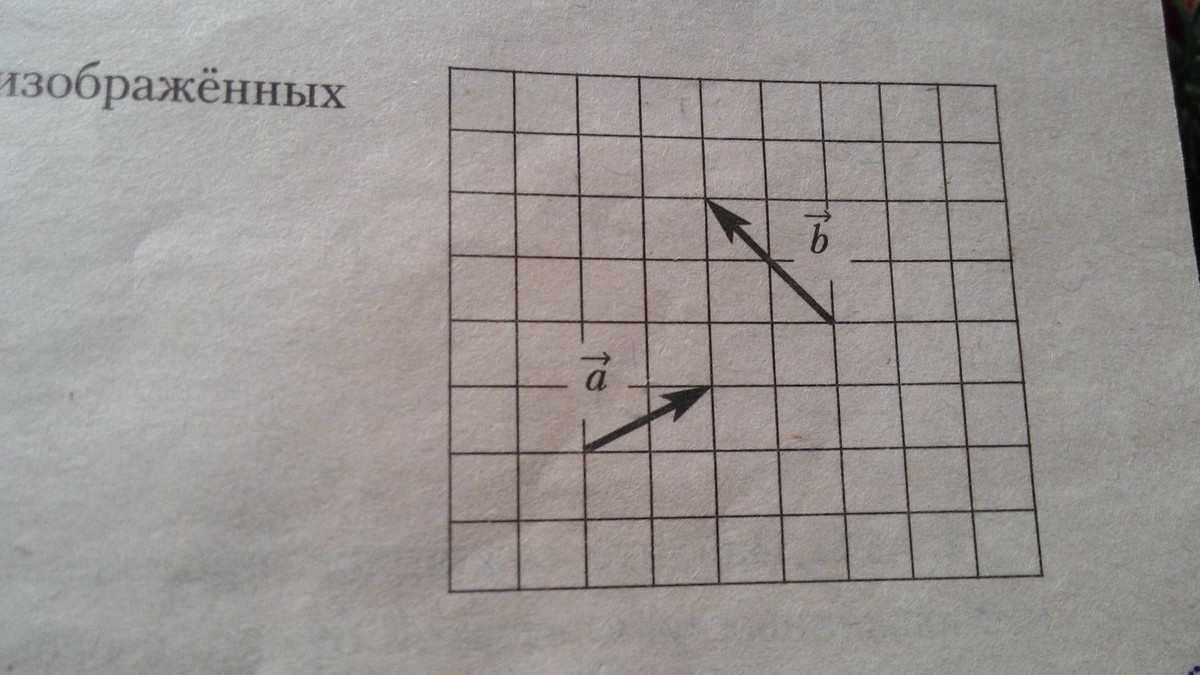
Найдите длину суммы векторов a и b, изображенных на клетчатой бумаге с размером клетки 1 на 1.

Длина $displaystyle vec$ равна 3·1 = 3 т.

К. размер клетки 1 на 1.

Видео:ВЫЧИТАНИЕ ВЕКТОРОВ ЧАСТЬ I #егэ #огэ #математика #геометрия #профильныйегэСкачать

Найдите площадь трапеции , изображенной на клетчатой бумаге с размером клетки 1см× 1см Ответ дайте в квадратных см?

Найдите площадь трапеции , изображенной на клетчатой бумаге с размером клетки 1см× 1см Ответ дайте в квадратных см.

Видео:егэ векторы решу егэ все задания №2 профильСкачать

Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см х 1 см?

Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см х 1 см.

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

На клетчатой бумаге с размером клетки 1×1 изоброжена трапеция ?

На клетчатой бумаге с размером клетки 1×1 изоброжена трапеция .

Найдите длину ее средней линии.

Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

На клетчатой бумаге с размером клетки 1х1 изображена трапеция?

На клетчатой бумаге с размером клетки 1х1 изображена трапеция.

Найдите длину её средней линии.

Видео:РАЗБИРАЕМ ВЫЧИТАНИЕ ВЕКТОРОВ ЧАСТЬ II 😊#shorts #математика #егэ #задачи #егэ2022 #огэ2022Скачать

Найдите (в см ^ 2) площадь многоугольника, изображенного на клетчатой бумаге с размером клетки 1 см× 1 см?

Найдите (в см ^ 2) площадь многоугольника, изображенного на клетчатой бумаге с размером клетки 1 см× 1 см.

Видео:Нахождение длины вектора через координаты. Практическая часть. 9 класс.Скачать

Найдите (в см ^ 2) площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1× 1 см?

Найдите (в см ^ 2) площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1× 1 см.

Видео:Вычитание векторов. 9 класс.Скачать

Найдите (в см ^ 22) площадь многоугольника, изображенного на клетчатой бумаге с размером клетки 1 см × 1 см?

Найдите (в см ^ 22) площадь многоугольника, изображенного на клетчатой бумаге с размером клетки 1 см × 1 см.

Видео:№918. Разложите векторы а , b , с , d , е и f , изображенные на рисунке 276, а, б, вСкачать

Найдите (в см ^ 2) площадь многоугольника, изображенного на клетчатой бумаге с размером клетки 1 см × 1 см?

Найдите (в см ^ 2) площадь многоугольника, изображенного на клетчатой бумаге с размером клетки 1 см × 1 см.

Видео:Вычитание векторов. Практическая часть. 9 класс.Скачать

Найдите (в см ^ 2) площадь многоугольника, изображенного на клетчатой бумаге с размером клетки 1 см × 1 см?

Найдите (в см ^ 2) площадь многоугольника, изображенного на клетчатой бумаге с размером клетки 1 см × 1 см.

Видео:ВЕКТОРЫ | Разбор НОВОГО задания из ЕГЭ 2024Скачать

На клетчатой бумаге с размером клетки 1х1 изображён прямоугольный треугольник Найдите длину его гипотенузы?

На клетчатой бумаге с размером клетки 1х1 изображён прямоугольный треугольник Найдите длину его гипотенузы.

На этой странице вы найдете ответ на вопрос Найдите длину суммы векторов a и b, изображенных на клетчатой бумаге с размером клетки 1 на 1?. Вопрос соответствует категории Геометрия и уровню подготовки учащихся 5 — 9 классов классов. Если ответ полностью не удовлетворяет критериям поиска, ниже можно ознакомиться с вариантами ответов других посетителей страницы или обсудить с ними интересующую тему. Здесь также можно воспользоваться «умным поиском», который покажет аналогичные вопросы в этой категории. Если ни один из предложенных ответов не подходит, попробуйте самостоятельно сформулировать вопрос иначе, нажав кнопку вверху страницы.

Составим параметрические уравнения прямой : На плоскости XOZ : y = 0 ⇒ Нашли значение параметра t для вычисления координат точки пересечения прямой с плоскостью. .

Https : / / ru — static. Z — dn. Net / files / d81 / ecc80dbfa11e21774a94326e0bdb5668. Jpg.

2х + 1х = 63° 3х = 63° х = 21° Ответ : 1 угол = 21° ; 2угол = 42°.

Попыталась написать более плнятно.

Угол FOE = 180 — 56 — 25 = 99 градусов.

АОД — это развернутый угол, т. Е. 180, т. О. угол ВОС = 180 — (56 + 25) = 99 Т. К. угол ВОС = ФОЕ, следовательно ФОЕ = 99.

Стороны, лежащие напротив этих углов, будут равны. Напротив угла С лежит сторона EP, напротив угла P лежит сторона EC. Значит, EP = EC.

Площадь параллелограмма равна сторона на высоту проведенную к это стороне значит высота равна 17 / 3, 4 = 5.

1. Р(ABDE) = AB + BD + DE + EAР(BEDC) = BE + ED + DC + CBодна сторона DE = ED для этих четырехугольников общая. BD = BE по условию. Из равенства углов следует, что треугольники BCD и BAE равны (по стороне и двум прилежащим к ней углам. )BC = BA и ..

Вершины треугольника лежат на окружности, значит его углы вписанные. Вписанный угол равен половине градусной меры дуги, на которую он опирается. Значит дуга АВ равна удвоенной градусной мере угла С, опирающегося на эту дугу.

Видео:Задание 3 (№27717) ЕГЭ по математике. Урок 80Скачать

Найти длину разности векторов

Видео:Сложение векторов. 9 класс.Скачать

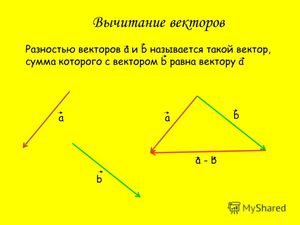
Определение разности двух векторов

В математике и физике студентам и школьникам зачастую попадаются задачи на векторные величины и на выполнение различных операций над ними. В чём же отличие векторных величин от привычных нам скалярных, единственная характеристика которых — это численное значение? В том, что они обладают направлением.
[block >

Видео:Выразить векторы. Разложить векторы. Задачи по рисункам. ГеометрияСкачать

Определения векторной математики

Введём главные определения, используемые при выполнении линейных операций.

1. Вектором называют направленный (имеющий точку начала и точку конца) отрезок.
2. Длина (модуль) — это длина направленного отрезка.
3. Коллинеарными называют такие два вектора, которые либо параллельны одной и той же прямой, либо одновременно лежат на ней.
4. Противоположно направленными векторами называют коллинеарные и при этом направленные в разные стороны. Если же их направление совпадает, то они являются сонаправленными.
5. Вектора являются равными, когда они сонаправлены и одинаковы по модулю.
6. Суммой двух векторов a и b является такой вектор c, начало которого совпадает с началом первого, а конец — с концом второго при условии, что b начинается в той же точке, в которой заканчивается a.
7. Разностью векторов a и b называют сумму a и (—b), где (—b) — противоположно направленный к вектору b. Также определение разности двух векторов может быть дано следующее: разностью c пары векторов a и b называют такой c, который при сложении с вычитаемым b образует уменьшаемое a.

Видео:Координаты вектора. 9 класс.Скачать

Аналитический метод

Аналитический способ подразумевает получение координат разности по формуле без построения. Возможно выполнить вычисление для плоского (двухмерного), объёмного (трёхмерного) или же n-мерного пространства.

Для двухмерного пространства и векторных величин a и b расчёты будут иметь следующий вид: c = .

В случае с добавлением третьей координаты расчёт будет проводиться аналогично, и для a и b координаты разности будут также получены попарным вычитанием: c = .

Видео:Нахождение длины вектора. Практическая часть. 9 класс.Скачать

Вычисление разности графически

Для того чтобы построить разность графическим способом, следует воспользоваться правилом треугольника. Для этого необходимо выполнить следующую последовательность действий:

1. По заданным координатам построить векторы, для которых нужно найти разность.
2. Совместить их концы (т. е. построить два направленных отрезка, равных заданным, которые будут оканчиваться в одной и той же точке).
3. Соединить начала обоих направленных отрезков и указать направление; результирующий будет начинаться в той же точке, где начинался вектор, являющийся уменьшаемым, и заканчиваться в точке начала вычитаемого.

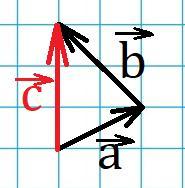
[block > Результат операции вычитания показан на рисунке ниже.

Также существует метод построения разности, незначительно отличающийся от предыдущего. Его суть заключается в применении теоремы о разности векторов, которая формулируется следующим образом: для того чтобы найти разность пары направленных отрезков, достаточно найти сумму первого из них с отрезком, противоположно направленным ко второму. Алгоритм построения будет иметь следующий вид:

1. Построить исходные направленные отрезки.
2. Тот, что является вычитаемым, необходимо отразить, т. е. построить противоположно направленный и равный ему отрезок; затем совместить его начало с уменьшаемым.
3. Построить сумму: соединить начало первого отрезка с концом второго.

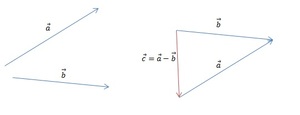
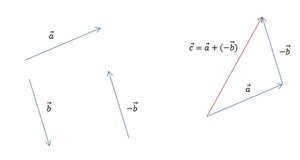
Результат такого решения изображён на рисунке:

Видео:СКАЛЯРНОЕ УМНОЖЕНИЕ ВЕКТОРОВ ЧАСТЬ I #математика #егэ #огэ #формулы #профильныйегэ #векторыСкачать

Решение задач

Для закрепления навыка разберём несколько заданий, в которых требуется рассчитать разность аналитически или графически.

Задача 1. На плоскости заданы 4 точки: A (1; —3), B (0; 4), C (5; 8), D (—3; 2). Определить координаты вектора q = AB — CD, а также рассчитать его длину.

Решение. Вначале следует найти координаты AB и CD. Для этого из координат конечных точек вычтем координаты начальных. Для AB началом является A (1; —3), а концом — B (0; 4). Рассчитаем координаты направленного отрезка:

Аналогичный расчёт выполняется для CD:

Теперь, зная координаты, можно найти разность векторов. Формула для аналитического решения плоских задач была рассмотрена ранее: для c = a — b координаты имеют вид = . Для конкретного случая можно записать:

Чтобы найти длину q, воспользуемся формулой | q | = √(q₁² + q₂²) = √((— 9)² + (— 1)²) = √(81 + 1) = √82 ≈ 9,06.
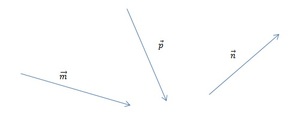
[block > Задача 2. На рисунке изображены векторы m, n и p.

Необходимо построить для них разности: p — n; m — n; m — n — p. Выяснить, какая из них обладает наименьшим модулем.

Решение. В задаче требуется выполнить три построения. Рассмотрим каждую часть задания более подробно.

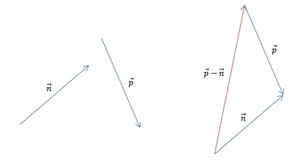
Часть 1. Для того чтобы изобразить p — n, воспользуемся правилом треугольника. Для этого при помощи параллельного переноса соединим отрезки так, чтобы совпала их конечная точка. Теперь соединим начальные точки и определим направление. В нашем случае вектор разности начинается там же, где и вычитаемый n.

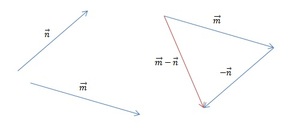
Часть 2. Изобразим m — n. Теперь для решения воспользуемся теоремой о разности векторов. Для этого следует построить вектор, противоположный n, а затем найти его сумму с m. Полученный результат будет выглядеть так:

[block > Часть 3. Для того чтобы найти разность m — n — p, следует разбить выражение на два действия. Поскольку в векторной алгебре действуют законы аналогичные законам арифметики, то возможны варианты:

• m — (n + p): в этом случае вначале строится сумма n + p, которая затем вычитается из m;
• (m — n) — p: здесь сначала нужно найти m — n, а затем отнять от этой разности p;
• (m — p) — n: первым действием определяется m — p, после чего из полученного результата нужно вычесть n.

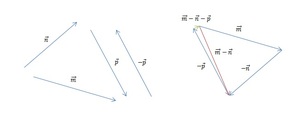
Так как в предыдущей части задачи мы уже нашли разность m — n, нам остаётся лишь вычесть из неё p. Построим разность двух данных векторов при помощи теоремы о разности. Ответ показан на изображении ниже (красным цветом обозначен промежуточный результат, а зелёным — окончательный).

Остаётся определить, модуль какого из отрезков является наименьшим. Вспомним, что понятия длины и модуля в векторной математике являются идентичными. Оценим визуально длины p — n, m — n и m — n — p. Очевидно, что самым коротким и обладающим наименьшим модулем является ответ в последней части задачи, а именно m — n — p.
[block > [block >

Видео:10 класс, 40 урок, Сложение и вычитание векторовСкачать

Как найти разность векторов

Видео:Угол между векторами | МатематикаСкачать

Формула

Видео:ПРОФИЛЬ 2024. Задание 2. Векторы. Все задачи с ромбом.Скачать

Примеры нахождения разности векторов

Задание. Найти разность векторов $bar-bar$, где $bar=(3 ; 0)$ и $bar=(1 ; 2)$

Решение. Для нахождения разности векторов $bar$ и $bar$, вычтем их соответствующие координаты:

Решение. Для нахождения искомой разности векторов вычтем их соответствующие координаты:

Видео:8 класс, 46 урок, Вычитание векторовСкачать

Остались вопросы?

Здесь вы найдете ответы.

Поможем выполнить
любую работу

Все еще сложно?

Наши эксперты помогут разобраться

Не получается написать работу самому?

Доверь это кандидату наук!

Ищещь ответ на вопрос с которым нужна помощь?

Сумма и разность векторов

В данной публикации мы рассмотрим, как найти сумму и разность векторов, приведем геометрическую интерпретацию, а также формулы, свойства и примеры этих действий.

Сумма векторов

Сложение векторов выполняется по правилу треугольника.

Геометрическая интерпретация:

Суммой a и b является вектор c , начало которого совпадает с началом a , а конец – с концом b . При этом конец вектора a должен совпадать с началом вектора b .

Для сложения векторов также используется правило параллелограмма.

Два неколлинеарных вектора a и b можно привести к общему началу, и в этом случае их суммой является вектор c , совпадающий с диагональю параллелограмма и берущий начало в той же точке, что и исходные векторы.

Формула сложения векторов

Элементы вектора c равняются попарной сумме соответствующих элементов a и b .

<td data-cell-id="B1" data-x="1" data-y="1" data-db-index="1" data-cell-type="text" data-original-value=" a + b = x + b_x; a_y + b_y> » data-order=» a + b = x + b_x; a_y + b_y> » style=»min-width:55.0847%; width:55.0847%;»> a + b = x + b_x; a_y + b_y>

<td data-cell-id="B2" data-x="1" data-y="2" data-db-index="2" data-cell-type="text" data-original-value=" a + b = x + b_x; a_y + b_y; a_z + b_z> » data-order=» a + b = x + b_x; a_y + b_y; a_z + b_z> «> a + b = x + b_x; a_y + b_y; a_z + b_z>

<td data-cell-id="B3" data-x="1" data-y="3" data-db-index="3" data-cell-type="text" data-original-value=" a + b = 1 + b₁; a₂ + b₂; . a_n + b_n> » data-order=» a + b = 1 + b₁; a₂ + b₂; . a_n + b_n> «> a + b = 1 + b₁; a₂ + b₂; . a_n + b_n>

Свойства сложения векторов

1. Коммутативность: a + b = b + a

2. Ассоциативность: ( a + b ) + c = a + ( b + c )

3. Прибавление к нулю: a + 0 = a

4. Сумма противоположных векторов: a + (- a ) = 0

Примечание: Вектор – a коллинеарен и равен по длине a , но имеет противоположное направление, из-за чего называется противоположным.

Разность векторов

Для вычитания векторов также применяется правило треугольника.

Если из вектора a вычесть b , то получится c , причем должно соблюдаться условие:

Формула вычитания векторов

Элементы вектора c равны попарной разности соответствующих элементов a и b .

<td data-cell-id="B1" data-x="1" data-y="1" data-db-index="1" data-cell-type="text" data-original-value=" a — b = x — b_x; a_y — b_y> » data-order=» a — b = x — b_x; a_y — b_y> » style=»min-width:55.0847%; width:55.0847%;»> a — b = x — b_x; a_y — b_y>

<td data-cell-id="B2" data-x="1" data-y="2" data-db-index="2" data-cell-type="text" data-original-value=" a — b = x — b_x; a_y — b_y; a_z — b_z> » data-order=» a — b = x — b_x; a_y — b_y; a_z — b_z> «> a — b = x — b_x; a_y — b_y; a_z — b_z>

<td data-cell-id="B3" data-x="1" data-y="3" data-db-index="3" data-cell-type="text" data-original-value=" a — b = 1 — b₁; a₂ — b₂; . a_n — b_n> » data-order=» a — b = 1 — b₁; a₂ — b₂; . a_n — b_n> «> a — b = 1 — b₁; a₂ — b₂; . a_n — b_n>

Примеры задач

Задание 1
Вычислим сумму векторов и .

Задание 2
Найдем разность векторов и .

Задание по геометрии — вектора.

Эта страница посвящена группе задач по геометрии, связанной с векторами, и является продолжением рассмотрения серии геометрических заданий, характерных для ЕГЭ и ОГЭ по математике.
Если вы не занимались другими типами этого задания, перейдите по ссылкам в конце страницы.

Задачи на вектора.

Длина отрезка называется модулем вектора. Два вектора равны, если они имеют равные модули и одинаково направлены.
Вектора обозначают либо строчными латинскими буквами a, b, c . , либо указанием концов отрезка AB, CD, MN. Чтобы отличить обозначение вектора от обозначения просто отрезка, эти символы сверху дополняются черточками или стрелочками. В печатном тексте строчные латинские буквы часто выделяют только полужирным шрифтом.

Если вектор обозначен двумя буквами (концами отрезка), то на первом месте всегда стоит начало вектора.

Задать вектор можно разными способами:
1. Графически — изобразить на координатной сетке.
2. Задать начальную и конечную точки и их координаты.
3. Задать длину отрезка и направление. Направление определяют углы с осями координат (направляющие косинусы).
4. Задать координаты вектора.

Уточним понятие координаты вектора.

На рисунке вектор AB имеет координаты (9;5). Обратите внимание, что эти числа фактически задают катеты прямоугольного треугольника, гипотенузой которого является отрезок АВ. Длина этих катетов не изменится, если мы переместим параллельным переносом отрезок, а с ним и весь треугольник, в другое место. Координаты вектора не зависят от его положения на плоскости, а только от длины отрезка и направления. Если направление вектора не совпадает с направлением оси координат, то соответствующая координата вектора будет равна длине катета со знаком «минус».

Вектора можно складывать, вычитать, умножать на число. Для векторов также определены специальные виды умножения — скалярное произведение, результатом которого является число, и — векторное произведение, результатом которого является вектор. (Векторное произведение не входит в обязательную школьную программу по математике, но частично встречается на уроках физики, когда изучают законы индукции магнитного поля.) Операции над векторами можно производить либо координатным методом, либо графическим (правило параллелограмма, правило треугольника. ). Повторите эти правила по учебнику или справочнику и выберите себе «любимое». Я привожу решение тем методом, который короче для конкретной задачи.

Для следующей группы задач чертёж в условии, вообще говоря, не обязателен. Если решать задачи координатным методом, то и в решении можно обойтись без чертежа, тем более, не нужна сетка. Однако лучше чертежи делать всегда, чтобы избежать нечаянных ошибок. А сетка помогает зрительно контролировать своё решение. Конечно, в том случае, если масштаб данных позволяет.

Две стороны прямоугольника ABCD равны 6 и 8.
Найдите длину вектора AC .

Длина вектора AC — равна длине отрезка AC, который является гипотенузой прямоугольного треугольника ABC с известными катетами.
AC 2 = AB 2 + BC 2 = 8 2 + 6 2 = 64 + 36 = 100; AC = 10.

Ответ: 10

Две стороны прямоугольника ABCD равны 6 и 8.
Найдите длину суммы векторов AB и AD .

По правилу параллелограмма: сумма векторов совпадает с диагональю параллелограмма, проходящей через точку, в которой совмещены начала векторов-слагаемых; начало вектора-суммы находится в точке начала обоих векторов. На рисунке это вектор AC — . Его длину мы находили в предыдущей задаче:
AC 2 = AB 2 + BC 2 = 8 2 + 6 2 = 64 + 36 = 100; AC = 10.

Ответ: 10

Две стороны прямоугольника ABCD равны 6 и 8.
Найдите длину разности векторов AB и AD .

По правилу параллелограмма: разность векторов совпадает с другой диагональю параллелограмма (соединяющей концы векторов-слагаемых, если их начала совмещены в одной точке); вектор разности направлен от вычитаемого к уменьшаемому. На рисунке это вектор DB — , направлен от D к B, так как я нахожу разность AB — − AD — .
DB 2 = AB 2 + AD 2 = 8 2 + 6 2 = 64 + 36 = 100; DB = 10.

Ответ: 10

Замечание: Ответы совпали, потому что дан один и тот же прямоугольник, а диагонали в прямоугольнике, как известно, равны.

Две стороны прямоугольника ABCD равны 6 и 8.
Найдите скалярное произведение векторов AB и AD .

Скалярное произведение двух векторов a и b находится по любой из двух формул.
1) Через координаты по формуле (a,b) = a₁·b₁ + a₂·b₂
2) Через длины векторов и угол между ними по формуле (a,b) = |a|·|b|·cosα

Способ I.
Координаты вектора AB — равны (8;0), вектора AD — равны (0;6).
Значит ( AB — , AD — ) = 8·0 + 0·6 = 0.
Способ II.
| AB — | = AB = 8, | AD — | = AD = 6, cosα = cos∠DAB = cos90° = 0.
Значит ( AB — , AD — ) = | AB — |·| AD — |·cos∠DAB = 8·6·0 = 0.

Ответ: 0

Замечание: Есть несколько способов обозначения скалярного произведения. Можно со скобками (a,b) или без них a·b _ _ , как обычное умножение.

Две стороны прямоугольника ABCD равны 6 и 8.
Диагонали пересекаются в точке O. Найдите длину суммы векторов AO и BO .

Вспомним, что диагонали прямоугольника пересекаются в его центре и в точке пересечения делятся пополам.

Способ I.
Координаты вектора AO — равны (4;3), обе положительны, потому что вектор направлен вверх, как ось Oy и вправо, как ось Ox. Координаты вектора BO — равны (-4;3), вектор направлен вверх, как ось Oy, но влево, противоположно оси Ox. Чтобы найти сумму векторов, воспользуемся тем, что при сложении векторов их соответствующие координаты складываются. Пусть вектор s(s₁;s₂) — сумма, тогда s₁ = 4 + (- 4) = 4 — 4 = 0; s₂ = 3 + 3 = 6. Квадрат длины вектора |s| 2 = s₁ 2 + s₂ 2 = 0 2 + 6 2 = 36;
длина вектора |s| = 6.

Способ II.
Чтобы решить задачу графически, надо применить к одному или к обоим векторам параллельный перенос. Для применения правила параллелограмма надо сместить их так, чтобы обе начальные точки совпали. Для применения правила треугольника надо начало одного из векторов-слагаемых совместить с концом другого. Здесь сместили вектор BO — вдоль линии ВD. На рисунке показан результат графического сложения — это вектор AD — . Как видно непосредственно по рисунку, его длина равна 6.

Ответ: 6

Две стороны прямоугольника ABCD равны 6 и 8.
Диагонали пересекаются в точке O. Найдите длину разности векторов AO и BO .

‘Способ I.
Координаты вектора AO — равны (4;3), вектора BO — равны (-4;3). Чтобы найти разность векторов, нужно найти разность их соответствующих координат. Пусть вектор d(d₁;d₂) — разность, тогда d₁ = 4 — (- 4) = 4 + 4 = 8; d₂ = 3 — 3 = 0. Квадрат длины вектора |d| 2 = d₁ 2 + d₂ 2 = 8 2 + 0 2 = 64; длина вектора |d| = 8.

Способ II.
Чтобы решить задачу графически, совмещаем начала векторов параллельным переносом обоих векторов вдоль диагоналей прямоугольника. На рисунке показан результат графического вычитания — это вектор DС — . Как видно непосредственно по рисунку, его длина равна 8.

Ответ: 8

Продолжить и повторить решение типовых задач ЕГЭ по математике на темы:

Перейдите по стрелке, чтобы найти ссылки на другие задачи ЕГЭ по математике.