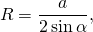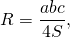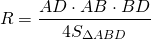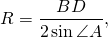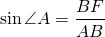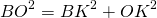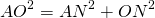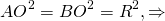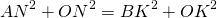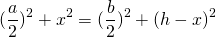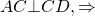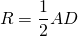Трапеция — это геометрическая фигура с четырмя углами. При построении трапеции важно учитывать, что две противоположные стороны параллельны, а две другие, наоборот, не параллельны относительно друг друга. Это слово пришло в современность из Древней Греции и звучало как «трапедзион», что означало «столик», «обеденный столик».
Эта статья рассказывает о свойствах трапеции, описанной около окружности. Также мы рассмотрим виды и элементы этой фигуры.
- Элементы, виды и признаки геометрической фигуры трапеция
- Свойства трапеции, описанной около окружности
- Еще немного о свойствах трапеции, заключенной в окружность
- Равнобедренная трапеция. Формулы, признаки и свойства равнобедренной трапеции
- Признаки равнобедренной трапеции
- Основные свойства равнобедренной трапеции
- Стороны равнобедренной трапеции
- Формулы длин сторон равнобедренной трапеции:
- Средняя линия равнобедренной трапеции
- Формулы длины средней линии равнобедренной трапеции:
- Высота равнобедренной трапеции
- Формулы определения длины высоты равнобедренной трапеции:
- Диагонали равнобедренной трапеции
- Формулы длины диагоналей равнобедренной трапеции:
- Площадь равнобедренной трапеции
- Формулы площади равнобедренной трапеции:
- Окружность описанная вокруг трапеции
- Формула определения радиуса описанной вокруг трапеции окружности:
- Радиус описанной окружности трапеции
- 💡 Видео
Видео:Основания равнобедренной трапеции равны 72 и 30. Центр окружности, описанной около трапеции... (ЕГЭ)Скачать
Элементы, виды и признаки геометрической фигуры трапеция
Параллельные стороны в этой фигуре называют основаниями, а те, что не параллельны — боковыми сторонами. При условии, что боковые стороны одинаковой длины, трапеция считается равнобедренной. Трапеция, боковые стороны которой лежат перпендикулярно основанию под углом в 90°, называется прямоугольной.
У этой, казалось бы, незамысловатой фигуры имеется немалое количество свойств, ей присущих, подчеркивающих ее признаки:
- Если провести среднюю линию по боковым сторонам, то она будет параллельна основаниям. Этот отрезок будет равен 1/2 разности оснований.
- При построении биссектрисы из любого угла трапеции образуется равносторонний треугольник.
- Из свойств трапеции, описанной около окружности, известно, что сумма параллельных боковых сторон должна быть равна сумме оснований.
- При построении диагональных отрезков, где одна из сторон является основанием трапеции, полученные треугольники будут подобны.
- При построении диагональных отрезков, где одна из сторон является боковой, полученные треугольники будут иметь равную площадь.
- Если продолжить боковые линии и построить отрезок из центра основания, то образованный угол будет равен 90°. Отрезок, соединяющий основания, будет равен 1/2 их разности.
Видео:Радиус описанной окружности трапецииСкачать
Свойства трапеции, описанной около окружности
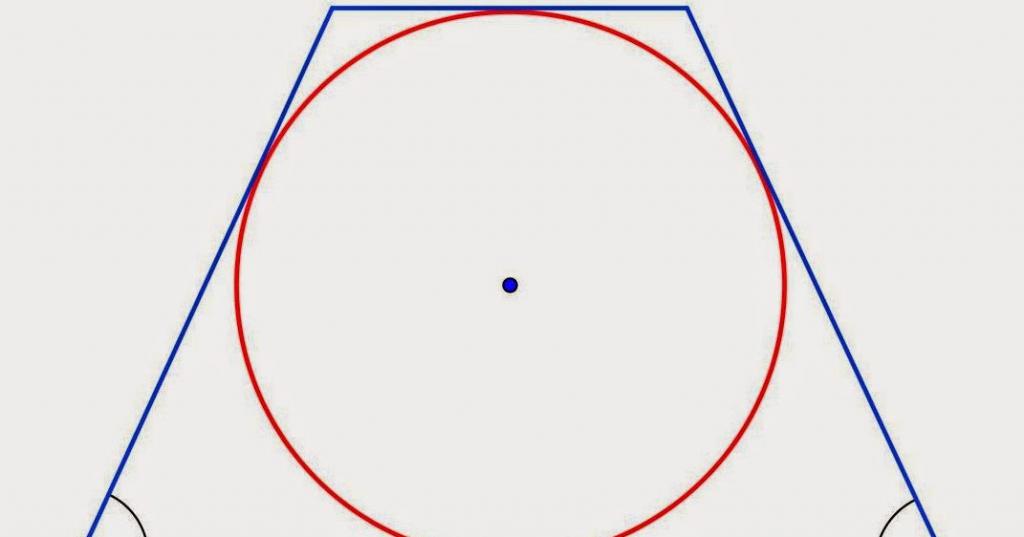
Заключить окружность в трапецию возможно лишь при одном условии. Данное условие заключается в том, что сумма боковых сторон должна быть ровна сумме оснований. Например, при построении трапеции AFDM применимо AF + DM = FD + AM. Только в таком случае в трапецию можно заключить круг.
Итак, подробнее о свойствах трапеции, описанной около окружности:
- Если в трапецию заключена окружность, то для того, чтобы найти длину ее линии, пересекающей фигуру пополам, необходимо найти 1/2 от суммы длин боковых сторон.
- При построении трапеции, описанной около окружности, образованная гипотенуза тождественна радиусу круга, а высота трапеции по совместительству является и диаметром круга.
- Еще одним свойством равнобедренной трапеции, описанной около окружности, является то, что ее боковая сторона сразу видна от центра окружности под углом 90°.
Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать
Еще немного о свойствах трапеции, заключенной в окружность
Только равнобедренная трапеция может быть вписана в окружность. Это значит, что нужно соблюсти условия, при которых построенная трапеция AFDM будет отвечать следующим требованиям: AF + DM = FD + MA.
Теорема Птолемея гласит, что в трапеции, заключенной в окружность, произведение диагоналей тождественно и равно сумме умноженных противоположных сторон. Это значит, что при построении окружности, описанной около трапеции AFDM, применимо: AD × FM = AF × DM + FD × AM.
На школьных экзаменах довольно часто встречаются задачи, требующие решения задач с трапецией. Большое количество теорем необходимо запоминать, но если выучить сразу не получиться — не беда. Лучше всего периодически прибегать к подсказке в учебниках, чтобы эти знания сами собой, без особого труда уложились в голове.
Видео:Задача про трапецию, описанную около окружностиСкачать
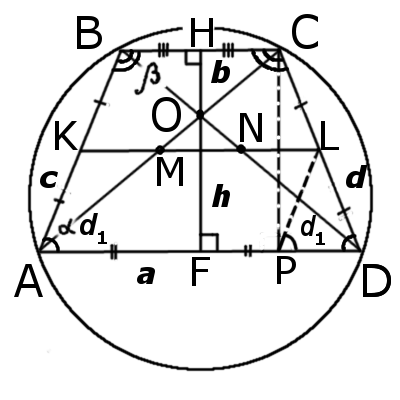
Равнобедренная трапеция. Формулы, признаки и свойства равнобедренной трапеции
 |
| Рис.1 |
Видео:ОГЭ по математике. Задание 15Скачать
Признаки равнобедренной трапеции
∠ABC = ∠BCD и ∠BAD = ∠ADC
∠ABD = ∠ACD, ∠DBC = ∠ACB, ∠CAD = ∠ADB, ∠BAC = ∠BDC
∠ABC + ∠ADC = 180° и ∠BAD + ∠BCD = 180°
Видео:Вписанная и описанная окружность - от bezbotvyСкачать
Основные свойства равнобедренной трапеции
∠ABC + ∠BAD = 180° и ∠ADC + ∠BCD = 180°
AC 2 + BD 2 = AB 2 + CD 2 + 2BC · AD
9. Высота (CP), опущенная из вершины (C) на большее основание (AD), делит его на большой отрезок (AP), который равен полусумме оснований и меньший (PD) — равен полуразности оснований:
| AP = | BC + AD |
| 2 |
| PD = | AD — BC |
| 2 |
Видео:Геометрия Задача № 26 Найти радиус вписанной в трапецию окружностиСкачать
Стороны равнобедренной трапеции
Формулы длин сторон равнобедренной трапеции:
a = b + 2 h ctg α = b + 2 c cos α
b = a — 2 h ctg α = a — 2 c cos α
| c = | h | = | a — b |
| sin α | 2 cos α |
2. Формула длины сторон трапеции через диагонали и другие стороны:
| a = | d 1 2 — c 2 | b = | d 1 2 — c 2 | c = √ d 1 2 — ab |
| b | a |
3. Формулы длины основ через площадь, высоту и другую основу:
| a = | 2S | — b b = | 2S | — a |
| h | h |
4. Формулы длины боковой стороны через площадь, среднюю линию и угол при основе:
| с = | S |
| m sin α |
5. Формулы длины боковой стороны через площадь, основания и угол при основе:
| с = | 2S |
| ( a + b ) sin α |
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать
Средняя линия равнобедренной трапеции
Формулы длины средней линии равнобедренной трапеции:
m = a — h ctg α = b + h ctg α = a — √ c 2 — h 2 = b + √ c 2 — h 2
2. Формула средней линии трапеции через площадь и сторону:
| m = | S |
| c sin α |
Видео:Свойство окружности, описанной около равнобедренного треугольникаСкачать
Высота равнобедренной трапеции
Формулы определения длины высоты равнобедренной трапеции:
1. Формула высоты через стороны:
| h = | 1 | √ 4 c 2 — ( a — b ) 2 |
| 2 |
2. Формула высоты через стороны и угол прилегающий к основе:
| h = | a — b | tg β | = c sin β |
| 2 |
Видео:Малоизвестные свойства равнобедренной трапеции. Разбор задачи 17 ЕГЭ профиль.Скачать
Диагонали равнобедренной трапеции
Формулы длины диагоналей равнобедренной трапеции:
d 1 = √ a 2 + c 2 — 2 ac cos α
d 1 = √ b 2 + c 2 — 2 bc cos β
4. Формула длины диагонали через высоту и основания:
| d 1 = | 1 | √ 4 h 2 + ( a + b ) 2 |
| 2 |
Видео:Вписанный в окружность четырёхугольник.Скачать
Площадь равнобедренной трапеции
Формулы площади равнобедренной трапеции:
1. Формула площади через стороны:
| S = | a + b | √ 4 c 2 — ( a — b ) 2 |
| 4 |
2. Формула площади через стороны и угол:
S = ( b + c cos α ) c sin α = ( a — c cos α ) c sin α
3. Формула площади через радиус вписанной окружности и угол между основой и боковой стороной:
| S = | 4 r 2 | = | 4 r 2 |
| sin α | sin β |
4. Формула площади через основания и угол между основой и боковой стороной:
| S = | ab | = | ab |
| sin α | sin β |
5. Формула площади ранобедренной трапеции в которую можно вписать окружность:
S = ( a + b ) · r = √ ab ·c = √ ab ·m
6. Формула площади через диагонали и угол между ними:
| S = | d 1 2 | · sin γ | = | d 1 2 | · sin δ |
| 2 | 2 |
7. Формула площади через среднюю линию, боковую сторону и угол при основании:
S = mc sin α = mc sin β
8. Формула площади через основания и высоту:
| S = | a + b | · h |
| 2 |
Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать
Окружность описанная вокруг трапеции
Формула определения радиуса описанной вокруг трапеции окружности:
1. Формула радиуса через стороны и диагональ:
| R = | a·c·d 1 |
| 4√ p ( p — a )( p — c )( p — d 1) |
где
| p = | a + c + d 1 |
| 2 |
a — большее основание
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать
Радиус описанной окружности трапеции
Как найти радиус описанной окружности для трапеции?
В зависимости от данных условия, сделать это можно разными способами. Готовой формулы радиуса описанной около трапеции окружности нет.
I. Радиус описанной около трапеции окружности как радиус окружности, описанной около треугольника, вершины которого — вершины трапеции
Описанная около трапеции окружность проходит через все её вершины, следовательно, является описанной для любого из треугольников, вершины которых являются вершинами трапеции.
В общем случае радиус описанной около треугольника окружности может быть найден по одной из формул
где a — сторона треугольника, α — противолежащий ей угол;
либо по формуле
где a, b, c — стороны, S — площадь треугольника.
Для трапеции ABCD радиус может быть найден, например, как радиус окружности, описанной около треугольника ABD:
где синус угла A можно найти из прямоугольного треугольника ABF:
III. Радиус описанной около трапеции окружности как расстояние до точки пересечения серединных перпендикуляров
Радиус описанной окружности — точка пересечения серединных перпендикуляров с сторонам трапеции. (Можно рассуждать иначе: в равнобедренном треугольнике AOD (AO=OD=R) высота ON является также медианой. Для треугольника BOC — аналогично).
Если известна высота трапеции KN=h, основания AD=a, BC=b, можно обозначить ON=x.
Если центр окружности лежит внутри трапеции, OK=h-x, из прямоугольных треугольников ANO и BKO можно выразить
и приравнять правые части
Решив это уравнения относительно x, можно найти R.
IV. Если диагональ трапеции перпендикулярна боковой стороне, центр описанной окружности лежит на середине большего основания и радиус равен половине большего основания.
точка O — середина AD
Если диагональ трапеции образует с боковой стороной тупой угол, центр описанной окружности лежит вне трапеции, за большим основанием.
I вариант нахождения радиуса для этого случая не изменяется.
Во II случае OK=h+x, соответственно, изменяется уравнение для нахождения x и R.
Позже рассмотрим конкретные задачи нахождения радиуса описанной около трапеции окружности.
💡 Видео
Около трапеции описана окружностьСкачать
Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать
Вписанная и описанная около равнобедренного треугольника, окружностьСкачать
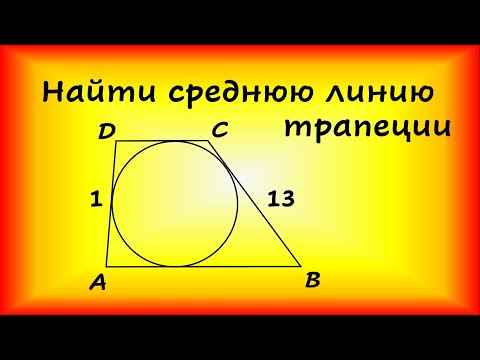
Боковые стороны трапеции, описанной около окружности, равны 13 и 1. Найдите среднюю линию трапеции.Скачать
SOS-ГЕОМЕТРИЯ! Отрезки и углы, смежные и вертикальные углы | Математика TutorOnlineСкачать
Трапеция и вписанная окружностьСкачать
Задача 6 №27926 ЕГЭ по математике. Урок 141Скачать
