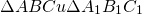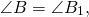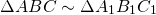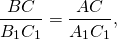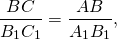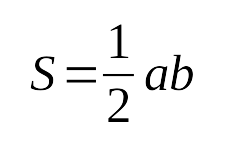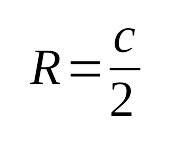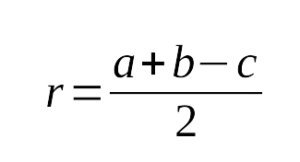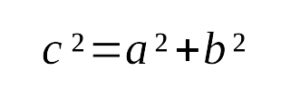Класс подобные прямоугольные треугольники

Подобие прямоугольных треугольников обычно доказывают, используя не общие признаки, а специальные признаки подобия для прямоугольных треугольников.

Признаки подобия прямоугольных треугольников

1- й признак подобия прямоугольных треугольников

( подобие прямоугольных треугольников по острому углу)

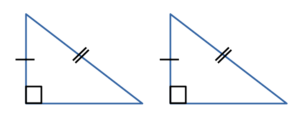
Если прямоугольные треугольники имеют равный острый угол, то такие треугольники подобны.

— прямоугольные (∠C=90º, ∠C=90º).

(по острому углу).

2- й признак подобия прямоугольных треугольников

( подобие прямоугольных треугольников по двум катетам)

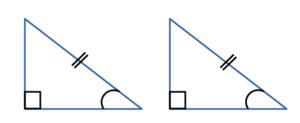
Если два катета одного прямоугольного треугольника пропорциональны двум катетам другого прямоугольного треугольника, то такие треугольники подобны.

— прямоугольные (∠C=90º, ∠C=90º).

(по двум катетам).

3- й признак подобия прямоугольных треугольников

( подобие прямоугольных треугольников по катету и гипотенузе)

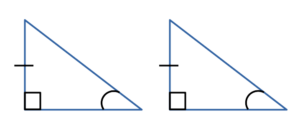
Если катет и гипотенуза одного прямоугольного треугольника пропорциональны катету и гипотенузе другого прямоугольного треугольника, то такие треугольники подобны.

— прямоугольные (∠C=90º, ∠C=90º).

(по катету и гипотенузе).

Из подобия прямоугольных треугольников следуют соотношения между высотой, проведённой к гипотенузе, гипотенузой, катетами и проекциями катетов на гипотенузу, а также свойство биссектрисы треугольника.

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Подобные треугольники

Видео:Подобие в прямоугольных треугольникахСкачать

Определение

Подобные треугольники — треугольники, у которых углы соответственно равны, а стороны одного соответственно пропорциональны сторонам другого треугольника.

Коэффициентом подобия называют число k , равное отношению сходственных сторон подобных треугольников.

Сходственные (или соответственные) стороны подобных треугольников — стороны, лежащие напротив равных углов.

Видео:Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать

Признаки подобия треугольников

I признак подобия треугольников

Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.

II признак подобия треугольников

Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.

Видео:Геометрия 7 класс (Урок№25 - Прямоугольные треугольники.)Скачать

Свойства подобных треугольников

• Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
• Отношение периметров подобных треугольников равно коэффициенту подобия.
• Отношение длин соответствующих элементов подобных треугольников (в частности, длин биссектрис, медиан, высот и серединных перпендикуляров) равно коэффициенту подобия.

Видео:Решение прямоугольных треугольников. Практическая часть. 8 класс.Скачать

Примеры наиболее часто встречающихся подобных треугольников

1. Прямая, параллельная стороне треугольника, отсекает от него треугольник, подобный данному.

2. Треугольники и , образованные отрезками диагоналей и основаниями трапеции, подобны. Коэффициент подобия –

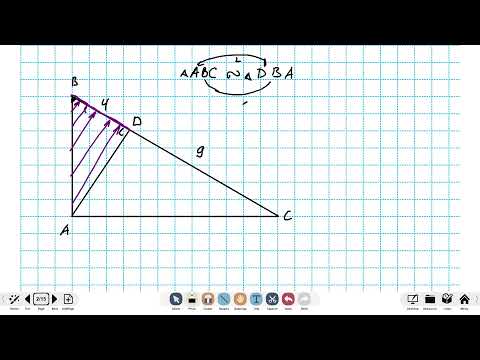
3. В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобных исходному.

Здесь вы найдете подборку задач по теме «Подобные треугольники» .

Видео:Подобие прямоугольных треугольников и его применениеСкачать

Прямоугольный треугольник: Признаки Равенства и Подобия

Видео:Как ПОНЯТЬ ГЕОМЕТРИЮ за 5 минут — Подобие ТреугольниковСкачать

Определение

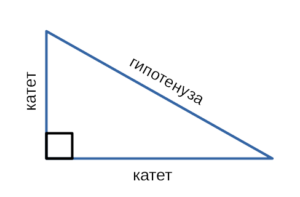
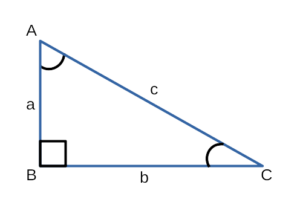
Прямоугольный треугольник — это треугольник, в котором один из углов прямой.

Гипотенуза в прямоугольном треугольнике — это сторона напротив прямого угла.

Катет в прямоугольном треугольнике — это две стороны прилежащие к прямому углу.

Видео:Подобие треугольников (ч.2) | Математика | TutorOnlineСкачать

Свойства прямоугольного треугольника

В прямоугольном треугольнике:

1. Сумма острых углов 90˚.
2. Катет, противолежащий углу в 30˚, равен половине гипотенузы.
3. Медиана, проведенная к гипотенузе, равна ее половине.
4. Центр описанной окружности — середина гипотенузы.
   

Формулы:

1. Площадь прямоугольного треугольника равна
   половине произведения катетов:
   
2. Радиус описанной окружности около прямоугольного
   треугольника равен половине гипотенузы:
   
3. Радиус вписанной окружности в прямоугольный треугольник
   выражается следующим образом:
   
4. Квадрат гипотенузы равен сумме квадратов катетов:

Видео:Подобие прямоуголных треугольников. 1 признак.Скачать

Признаки равенства прямоугольных треугольников

С помощью признаков равенства прямоугольных треугольников
можно доказать что прямоугольные треугольники равны.

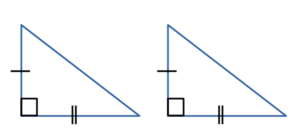
1. По двум катетам:
   Если два катета одного прямоугольного треугольника соответственно
   равны двум катетам другого прямоугольного треугольника,
   то такие треугольники равны.
   
2. По катету и гипотенузе:
   Если катет и гипотенуза одного прямоугольного треугольника соответственно
   равны катету и гипотенузе другого прямоугольного треугольника,
   то такие треугольники равны.
   
3. По гипотенузе и острому углу:
   Если гипотенуза и острый угол одного прямоугольного треугольника соответственно
   равны гипотенузе и острому углу другого прямоугольного треугольника,
   то такие треугольникиравны.
   
4. По катету и острому углу:
   Если катет и острый угол одного прямоугольного треугольника соответственно
   равны катету и острому углу другого прямоугольного треугольника,
   то такие треугольники равны.

Видео:Профильный ЕГЭ 2024. Задача 1. Прямоугольный треугольник. 10 классСкачать

Признаки прямоугольного треугольника

С помощью признаков прямоугольного треугольника можно
доказать, что треугольник прямоугольный.

1. По теореме Пифагора:
   Если квадрат стороны равен сумме квадратов двух других сторон,
   то треугольник прямоугольный.
2. По центру описанной окружности:
   Если центр описанной окружности лежит на стороне треугольника,
   то треугольник прямоугольный.
3. По медиане:
   Если медиана треугольника равна половине стороны, к которой она проведена,
   то треугольник прямоугольный.
4. По площади:
   Если площадь треугольника равна половине произведения двух его сторон,
   то треугольник прямоугольный.
5. По радиусу описанной окружности:
   Если радиус описанной окружности равен половине,
   то треугольник прямоугольный.

Видео:Свойства прямоугольного треугольника. 7 класс.Скачать

Признаки подобия прямоугольных треугольников

С помощью признаков подобия прямоугольных треугольников можно
доказать, что прямоугольные треугольники подобны.

💥 Видео

Всё про прямоугольный треугольник за 15 минут | Осторожно, спойлер! | Борис Трушин !Скачать

Математика | Соотношения между сторонами и углами в прямоугольном треугольнике.Скачать

Подобие прямоугольных треугольников. Геометрия 9 классСкачать

Свойства прямоугольного треугольника. Практическая часть. 7 класс.Скачать

Решение прямоугольных треугольников. Практическая часть. 8 класс.Скачать

Свойства подобных прямоугольных треугольников (видео 28) | Подобие. Геометрия | МатематикаСкачать

Подобие прямоугольных треугольников. Среднее геометрическое (пропорциональное). Геометрия 8-9 классСкачать

7 класс, 35 урок, Некоторые свойства прямоугольных треугольниковСкачать

Геометрия 7 Прямоугольные треугольникиСкачать