Нижняя граница индексации в MathCAD определена системной переменной ORIGIN. По умолчанию ORIGIN=0. Значение переменной можно переопределить. Например, ORIGIN=1.
Векторы и матрицы в MathCAD можно задавать путем ввода их элементов. Для ввода индекса элемента массива используется символ – [.
Поэлементный ввод массива Х
| Вводимые символы | Отображаемые символы |
| X [ 1 Shift+: 5 | X1:=5 |
| X [ 2 Shift+: 8 | X2:= 8 |
| X [ 3 Shift+: 10 | X3:= 10 |
Поэлементный ввод матрицы А
| Вводимые символы | Отображаемые символы |
| A [ 1,1 Shift+: 0.1 | A11 := 0.1 |
| A [ 1,2 Shift+: -2.5 | A12 := -2.5 |
| A [ 2,1 Shift+: -1.0 | A21 := -1.0 |
| A [ 2,2 Shift+: 5.2 | A22 := 5.2 |
Для операций с матрицами и векторами предназначена панель Matrix, которая открывается щелчком по кнопке 
в панели математических инструментов.
ПанельMatrix содержит следующие кнопки:
– определение размеров матрицы;
– ввод элемента массива 
;
– вычисление матрицы, обратной к данной 
;
– вычисление определителя матрицы 
;
– оператор векторизации (поэлементные операции с векторами и матрицами) 
;
– определение столбца матрицы 
;
– транспонирование матрицы 
;
– определение ранжированной переменной;
– вычисление скалярного произведения векторов;
– вычисление векторного произведения векторов;
– вычисление суммы компонент вектора.
– визуализация цифровой информации.
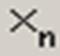
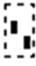
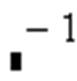
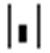
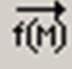
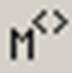
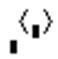
Действия, которые необходимо выполнить, чтобы ввести матрицу в рабочий документ при помощи кнопки 
панели Matrix:
1. Ввести с клавиатуры имя матрицы и знак присваивания;
2. Щелчком по кнопке 
открыть окно диалога:
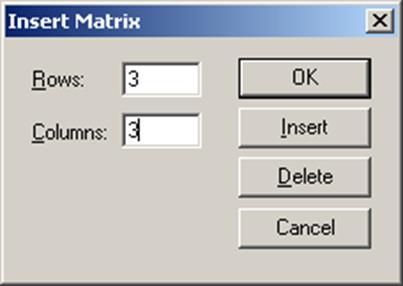
3. Определить число строк (Rows) и число столбцов (Columns) будущей матрицы;
4. Закрыть окно диалога, щелкнув по кнопке OK;
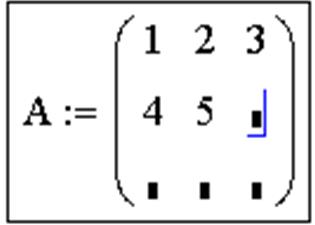
5. Ввести элементы матрицы, установив курсор в поле ввода, которое появится справа от знака присваивания:
Функции определения матриц и операции с блоками матриц:
matrix(m,n,f) – создает и заполняет матрицу A=<aij> размерности m на n, каждый элемент которой aij равен значению функции f(i,j);
diag(v) – создает диагональную матрицу, элементы главной диагонали которой хранятся в векторе v;
identity(n) – создает единичную матрицу порядка n;
augment(A,B) – из матриц А и В формируется третья матрица, первые столбцыкоторой содержат матрицу А, а последние — матрицу В (матрицы А и В должны иметь одинаковое число строк);
stack(A,B) – из матриц А и В формируется третья матрица, первые строкикоторой содержат матрицу А, а последние — матрицу В (матрицы А и В должны иметь одинаковое число столбцов);
submatrix(A,l,k,p,r) – формирует матрицу, которая является блоком матрицы А, расположенным в строках с l по k и в столбцах с p по r (l
Re(A) – возвращает матрицу (вектор) действительных частей матрицы (вектора) А с комплексными элементами;
Im(A) – возвращает матрицу (вектор) мнимых частей матрицы (вектора) А с комплексными элементами;
Функции вычисления различных числовых характеристик матриц:
last(v) – вычисление номера последнего элемента вектора v;
length(v) – вычисление количества элементов вектора v;
rows(A) – вычисление числа строк в матрице А;
cols(A) – вычисление числа столбцов в матрице А;
max(A) – вычисление наибольшего элемента в матрице (векторе) А;
min(A) – вычисление наименьшего элемента в матрице (векторе) А;
mean(A) – вычисление среднего значения матрицы (вектора) А;
tr(A) – вычисление следа (суммы диагональных элементов) квадратной матрицы А;
ranc(A) – вычисление ранга матрицы А;
Функции, реализующие численные алгоритмы:
rref(A) – приведение матрицы А к ступенчатому виду;
geninv(A) – вычисляет матрицу, левую обратную к матрице А, L∙A=E, где Е – единичная матрица размером n×n, L – прямоугольная матрица размером n×m, А – прямоугольная матрица размером m×n;
lsolve(A,b) – решение системы линейных алгебраических уравнений A∙x=b.
lu(A) – выполняет треугольное разложение матрицы А: A=С∙L∙U, где L и U – соответственно нижняя и верхняя треугольные матрицы, все четыре матрицы квадратные и одного порядка;
qr(A) – выполняет разложение матрицы А: A=Q∙R, где Q – ортогональная матрица, а R – верхняя треугольная матрицы;
cholesky(A) – выполняет разложение матрицы А по схеме Холецкого: А=L∙L T , где А — квадратная, симметричная, положительно определенная матрица, L – треугольная матрица;
sort(v) – сортировка элементов вектора v в порядке возрастания их значений;
reverse(v) – перестановка элементов вектора v в обратном порядке;
csort(A,n) – перестановка строк матрицы А таким образом, чтобы отсортированным оказался n-й столбец;
rsort(A,n) – перестановка столбцов матрицы А таким образом, чтобы отсортированной оказалась n-я строка.
ЗАДАЧА 1. Сформировать матрицу H из элементов матрицы D, исключив третий столбец и вторую строку.
ЗАДАЧА 2. Сформировать матрицу H следующим образом. Первая и последняя строки равны строкам матрицы D, остальные совпадают с матрицей C.
ЗАДАЧА 3. Сформировать матрицу таким образом, чтобы элементы на главной диагонали были равны 1, выше главной диагонали – 2, а ниже – 3.
ЗАДАЧА 4. Элементы матрицы формируются по формуле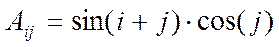 
. Сформировать вектор из максимальных элементов столбцов матрицы А. Найти сумму элементов матрицы, расположенных в четных строках.
ЗАДАЧА 5. Выполнить действия над матрицами А, В, С:
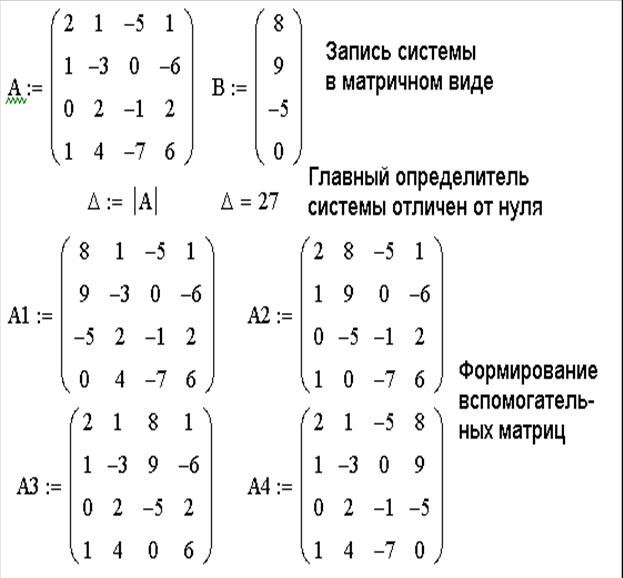
ЗАДАЧА 6. Решить систему линейных уравнений при помощи правила Крамера:
Для решения поставленной задачи необходимо выполнить следующие действия:
1. Сформировать матрицу системы А и вектор правых частей b.
2. Вычислить главный определитель ∆.
3. Сформировать вспомогательные матрицы (удобно скопировать матрицу А несколько раз и последовательно заменять в ней столбцы на вектор b) для вычисления определителей ∆i;
4. Вычислить определители ∆i;
5. Найти решение системы по формуле xi=∆i/∆.
ЗАДАЧА 7. Решить систему линейных уравнений методом обратной матрицы.
1. Сформировать матрицу коэффициентов и вектор свободных членов системы.
2. Решить систему, представив вектор неизвестных как произведение матрицы, обратной к матрице системы и вектора свободных членов.
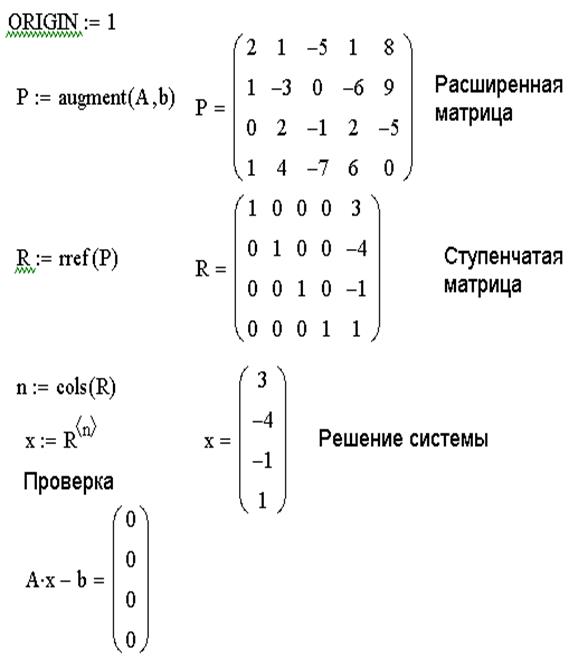
ЗАДАЧА 8. Решить систему линейных уравнений методом Гаусса.
Порядок решения задачи:
1. Сформировать матрицу коэффициентов и вектор свободных членов заданной системы.
2. Сформировать расширенную матрицу системы при помощи функции augment(A,b);
3. Используя функцию rref(A), привести расширенную матрицу к ступенчатому виду.
4. Получить решение системы, выделив последний столбец матрицы, полученной в предыдущем пункте.
5. Выполнить проверку Ax-B=0.
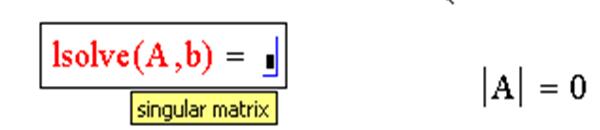
ЗАДАЧА 9. Решить систему при помощи функции lsolve:
Пример системы, которая не имеет решений:
Пример системы, которая имеет бесконечное множество решений
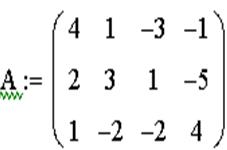
ЗАДАЧА 10. Решить систему при помощи решающего блока.
Решающий блок начинается с ключевого слова Given (Дано), которое необходимо ввести с клавиатуры.
Правее и ниже ключевого слова записываются уравнения системы.
Знак равенства в уравнениях вводится при помощи клавиш Ctrl+= или выбирается на панели инструментов Boolean.
Правее и ниже последнего уравнения системы вводится функция Find(x1,x2,…xn) (Найти), в скобках перечисляются имена переменных, значения которых нужно найти.
Численное решение системы можно получить, поставив знак равенства после функции Find(x1,x2,…xn).
Символьное решение получится, если после функции Find(x1,x2,…xn) указать знак стрелки, который находится в панели инструментов Symbolic (Ctrl+.).
Видео:7. MathCad. Векторы и матрицыСкачать
Лабораторная работа №4. Дискретная свертка и фильтрация сигнала
Цель работы: Изучить один из методов фильтрации сигналов с использованием алгоритма секционированной свертки.
Необходимые теоретические сведения
Демонстрация возможностей ДПФ для фильтрации сигнала была рассмотрена в работе №1. В данной работе рассмотрена фильтрация с помощью цифрового фильтра (ЦФ) на основе секционированной свертки и ДПФ.
Выходной сигнал цифрового фильтра можно рассчитать, используя соответствующие структуре фильтра разностные уравнения. Достоинством такого неэффективного подхода является то, что он наглядно демонстрирует работу ЦФ и позволяет определить многие характеристики ЦФ. Реакцию (выходной сигнал) y[n] ЦФ на произвольное входное воздействие x[n] можно представить с помощью импульсной характеристики фильтра h[n], которая по определению является откликом фильтра на единичный импульс d[n]. Соотношение, связывающее вход и выход ЦФ носит название линейной свертки, соответствует работе нерекурсивного фильтра и имеет вид
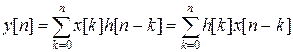 . | (1) |
Непосредственное вычисление по формулам (1) и (2) требует большого количества умножений: N1∙N2 для линейной свертки и N1(N2+1) для круговой. Для круговой свертки количество умножений можно уменьшить с помощью БПФ. Этот же метод можно использовать с небольшими изменениями и для линейной свертки.
Для этого последовательности x[n] и h[n] дополняются нулевыми отсчетами, число которых равно (N—N1) и (N—N2) соответственно для x[n] и h[n] до N1+N2-1 отсчета. Затем рассчитываются N — точечные ДПФ XN[k] и HN[k] и определяется их произведение YN[k]=XN[k]HN[k]. Наконец, с помощью обратного ДПФ для YN[k] рассчитывается круговая (периодическая) свертка yN[n], первые N=N1+N2-1 отсчетов которой соответствуют искомой линейной свертке, т.е. выходному сигналу ЦФ. Дополнение исходных последовательностей конечной длины x[n] и h[n] нулевыми отсчетами доводит период yN[n] до нужной величины N = N1+N2-1, что позволяет устранить наложения, характерные для круговой свертки.
Рассмотренный метод вычисления линейной свертки называется быстрой сверткой, поскольку использование алгоритмов БПФ позволяет существенно увеличить эффективность вычислений по сравнению с прямой сверткой, выполняемой в соответствии с (2).
На практике часто N1>>N2, причем величина N1 может быть очень большой (или вообще неизвестной — например, при обработке сигналов в реальном времени), поэтому при вычислениях в соответствии с приведенным выше алгоритмом быстрой свертки возникают большие задержки или вычисления невозможно выполнить из-за ограниченных ресурсов памяти. В этом случае применяется алгоритм секционированной свертки. Исходный сигнал разбивают на короткие участки (секции) длиной M, как правило, соизмеримые с длиной импульсной характеристики и отвечающие условию M ≥ N2, при котором перекрываются только две соседние i и (i +1)-я частичные свертки (рис.2). Результирующий сигнал y[n] ищется путем объединения результатов ДПФ на смежных участках длиной (N2-1), где N2 — длина импульсной характеристики.
 |
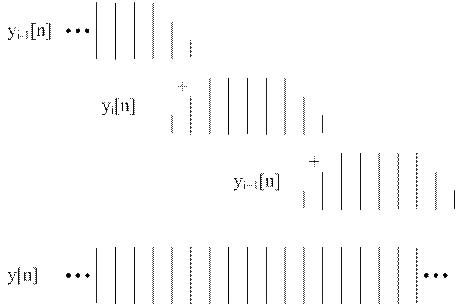| Рисунок 2 – Перекрытие с суммированием |
Обработка предыдущей секции сигнала при этом совмещается с записью новой, так что запаздывание выходного сигнала во времени не превышает длины одной секции.
Данный алгоритм секционированной свертки называется перекрытием с суммированием (overlap-add). Другой возможный вариант – перекрытие с накоплением (overlap-save). Входной сигнал разбивается на блоки, которые перекрываются по краям на (N2-1) отсчет. У получаемого выходного сигнала для каждого блока откидываются крайние участки длиной по (N2-1) отсчетов с каждого края. Потом секции объединяются без перекрытия. Результирующая последовательность будет иметь длину N=N1+N2-1.
Алгоритм секционированной свертки с суммированием
1. Пусть есть сигнал x[n], n=0, . N-1, N — такое большое, что сигнал не может поместиться в память, а может и бесконечное.
2. Есть импульсная характеристика фильтра h[n], n=0, . N2.
3. Разобьем сигнал x[n] на выборки по N1 отсчетов в каждой, N1 N2 (будем считывать из x[n] выборки по N1 значений).
5. Выберем из x[n] последовательность x1[n] длины N1 (первая выборка п.3).
7. Используя процедуру БПФ, вычислим преобразование Фурье X1[k], H[k], k=0, . L-1
9. С помощью обратного преобразования Фурье получим сигнал y1[n], n=0, . L-1. y1[n] — обратное БПФ от Y1[k].
10. Только первые N1+N2-1 отсчета последовательности y1[n] будут отличны от нуля. Но правильными будут только первые N1 отсчетов, которые мы и запоминаем в выходной последовательности y[n].
11. Оставшиеся N2 (N2-1, но для простоты захватим еще один нулевой отсчет) отсчета запоминаем во временном массиве t[n]: t[n]=y1[N1+n], n=0, . N2 — 1.
13. Далее алгоритм продолжается, пока не будет отфильтрован весь сигнал.
Графически описанный выше алгоритм показан на рис. 3. Для наглядности использованы промежуточные массивы x1[n], h1[n], y1[n], отличающие по длине от исходных x[n], h[n], y[n].
Т.к. на рис.3 первый этап выполняется иначе, чем второй и последующие, то на рис. 4 показан более удобный вариант для программной реализации.
 |
| Рисунок 3 – Алгоритм секционированной свертки |
 |
| Рисунок 4 – Алгоритм секционированной свертки для программирования |
Счетчик циклов-этапов k изменяется от 0 до некоторого значения, которое указывает, сколько раз блок считываемых данных N1 укладывается в N с округлением в большую сторону. Если же N бесконечно (или заранее неизвестно), то k увеличивается, пока на вход поступают данные.
Описание использования программного модуля
На рис. 5 показанное исходное состояние программы после запуска.
 |
| Рисунок 5 – Главное окно программного модуля |
На форме есть две кнопки «Открыть»: одна для входного сигнала, который необходимое отфильтровать, другая – для импульсной характеристики фильтра. Когда данные загрузятся, в поле «N=» будет показана длина сигнала, а в поле «N2=» длина импульсной характеристики.
После загрузки соответствующих файлов становится доступной поле ввода «Длина секции N1» и кнопка «Подготовить». Кнопку «Подготовить» необходимо использовать каждый раз после загрузки другого сигнала или импульсной характеристики, а также при изменении длины секции. В поле «Длина секции N1» необходимо ввести величину, большую чем в поле «N2=» (согласно алгоритму). Если данные корректные, то после нажатия кнопки «Подготовить» в поле «L= » появится значения длины секции для расчетов с помощью БПФ, а в поле «Раундов» — количество раундов расчетов (число секций).
После этого можно нажимать кнопку «Вычислить» или «Вычислить все». При нажатии первой из них будет выполнен расчет одного раунда, в поле «Раунд» отобразится цифра «1», а на графической панели «Отфильтрованный сигнал (результат свертки)» будет выведен результат расчетов (рис. 6).
 |
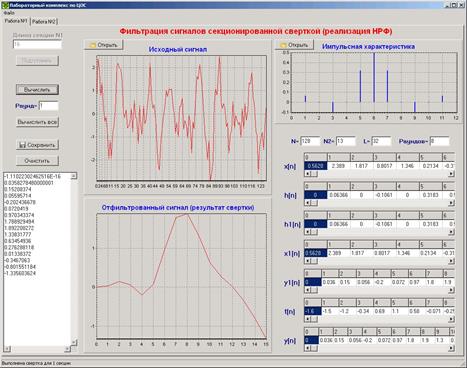| Рисунок 6 – Результат выполнения первого раунда фильтрации |
Кроме того, в числовом поле слева внизу окна программы будут показаны числовые значения расчетов, которые можно просмотреть с помощью полосы прокрутки или сохранить в файл. При повторном нажатии кнопки «Вычислить» будет рассчитан второй раунд (рис 7). При этом программа разработана так, чтобы количество раундов не превысило расчетное, после чего кнопки «Вычислить» и «Вычислить все» будут заблокированы. Кнопку «Вычислить все» можно нажать или с самого начала или в любой момент выполнения работы после нажатия кнопки «Вычислить». При этом сразу будет получен конечный результат, который выводится на график и который можно сохранить в файл при нажатии кнопки «Сохранить» (рис. 8).
Содержимое всех массивов данных можно просматривать во время счета с помощью таблиц, которые располагаются по правую сторону, под графической панелью «Импульсная характеристика» (рис. 6-8).
 |
| Рисунок 7 – Результат выполнения второго раунда фильтрации |
 |
| Рисунок 8 – Результат выполнения всех раундов фильтрации сигнала |
Порядок выполнения работы
Данная работа выполняется на ПЭВМ с использованием программы «Лабораторный комплекс по ЦОС» и MathCAD 15. До занятия выполняются пп. 1 и 2. На занятии – пп., начиная с 3.
1. Изучить работу с программным модулем «Фильтрация сигнала секционированной сверткой (реализация НРФ)» (далее для сокращения просто «Секционированная свертка»).
2. Разработать и нарисовать блок-схему алгоритма для программной реализации на MathCAD.
3. Запустить программный модуль «Секционированная свертка».
4. Считать с диска отсчеты измеренного сигнала и импульсную характеристику. Номер задания узнать у преподавателя.
5. Выполнить фильтрацию сигнала с помощью модуля «Секционированная свертка» и сохранить результат в файл на диск. На этом экспериментальная часть лабораторной работы заканчивается.
6. Запустить MathCAD.
7. Считать с диска отсчеты измеренного сигнала и импульсную характеристику. Построить графики введенных значений.
8. Используя приведенный на рис. 4 алгоритм и его текстовое описание, самостоятельно разработать в MathCAD программную реализацию.
9. Отфильтровать сигнал и построить в MathCAD выходной сигнал разработанного фильтра.
10. Ввести в MathCAD значения отфильтрованного сигнала, полученные в п.4 задания и сравнить с полученным результатом п.7. При правильной реализации п 7. результаты должны совпасть.
В отчете необходимо представить графики исходного и отфильтрованного сигналов, программу, написанную в MathCAD с пояснением всех операций и результаты сравнения работы программы MathCAD с результатом программного модуля «Секционированная свертка».
Вопросы к лабораторной работе
1. Каким методом в данной работе рассчитывается выходной сигнал ЦФ?
2. В чем достоинством метода расчета выходного сигнала ЦФ, который используется в данной работе?
3. С помощью какого выражения можно найти реакцию (выходной сигнал) ЦФ на произвольное входное воздействие? Как называется это соотношение?
4. Что такое импульсная характеристика фильтра? Как она обозначается?
5. Как выглядит выражение для выполнения z-преобразования импульсной характеристики?
6. Что такое круговая свертка? Когда она используется?
7. Как выглядит выражение для вычисления круговой свертки?
8. В каких случаях применяется алгоритм секционированной свертки? В чем его смысл?
9. Каким образом увеличивают скорость проведения вычислений при использовании секционированной свертки?
10. Почему выполнение первого этапа алгоритма по рис. 3 отличается от всех последующих этапов?
11. За счет чего удалось добиться унификации выполнения всех этапов алгоритма по рис. 4?
12. Что является счетчиком цикла (этапов)? Когда наступает конец выполнения программы?
Лабораторная работа №5. Синтез нерекурсивных цифровых фильтров (методом окон)
Цель работы: Изучить синтез нерекурсивных фильтров методом взвешивания.
Цифровой фильтр в узком смысле – это частотно-избирательная цепь, которая обеспечивает пропускание сигналов в определенных полосах частот и подавление в других. Область частот, в которой фильтр пропускает сигнал, называют полосой пропускания, а область частот, в которой ослабление входного сигнала велико — полосой задерживания. В зависимости от взаимного расположения полосы пропускания и полосы задерживания различают: фильтр нижних частот (ФНЧ), фильтр верхних частот (ФВЧ), полосовой фильтр (ПФ), заграждающий (режекторный) фильтр (ЗФ). Идеальные АЧХ указанных фильтров изображены на рис. 1.
 |
| Рисунок 1 – Идеальные АЧХ фильтров: а) фильтр нижних частот; б) фильтр верхних частот; в) полосовой фильтр; г) режекторный фильтр. |
По виду передаточной функции и соответственно, структуре, ЦФ делятся на две группы: нерекурсивные и рекурсивные.
Фильтры со структурой на рис. 2 носят название нерекурсивные (НРФ) (другой термин – трансверсальные) цифровые фильтры. Их работа подчиняется разностному уравнению 
, а передаточная функция равна 
.
 |
| Рисунок 2 – Структурная схема нерекурсивного (трансверсального) цифрового фильтра. |
Поскольку количество элементов задержки в реальном трансверсальном фильтре конечно, конечным является и количество ненулевых отсчетов импульсной характеристики фильтра, то есть импульсная характеристика такого фильтра конечна. Фильтры, обладающие таким свойством, принято выделять в отдельный класс и называть КИХ-фильтрами.
Основные достоинства КИХ-фильтров [2]:
1. КИХ-фильтры легко создавать со строго линейной фазовой характеристикой arg H(e j ω ).
2. КИХ-фильтры можно эффективно строить как по рекурсивным так и по нерекурсивным схемам.
3. КИХ-фильтры, реализуемые нерекурсивно, т.е. с помощью прямой свертки, всегда устойчивы.
4. При нерекурсивной реализации КИХ-фильтров шумы округления, возникающие за счет выполнения арифметических операций с конечной точностью, легко минимизировать.
5. Может быть адаптивным.
6. Легкое понимание принципов работы и проектирования.
Недостатки КИХ-фильтров [2]:
1. Для аппроксимации фильтров, частотные характеристики которых имеют острые срезы, требуется импульсная характеристика с большим числом отсчетов N. Поэтому при обычной свертке необходимо выполнять большой объем вычислений.
2. Задержка в КИХ-фильтрах с линейной фазовой характеристикой не всегда равна целому числу интервалов дискретизации. В некоторых приложениях такая некратная задержка может вызвать определенные трудности.
Реальные цифровые фильтры, обрабатывающие временные дискретные сигналы, должны отвечать принципу причинности, согласно которому сигнал на выходе не может появиться до прихода первого ненулевого отсчета входного сигнала. Такие фильтры называются физически реализуемыми или каузальными фильтрами, их импульсная характеристика должна подчиняться требованию:
| h[n] = 0 при n j ω ) – форме, неравномерности. 3. Выбор метода аппроксимации АЧХ (может выбираться разработчиком). При синтезе ЦФ вместо частот среза ωС, ωСН, ωСВ (рис. 1) могут задаваться частоты ωЗ и ωП, ωЗН и ωПН, ωЗВ и ωПВ, соответственно (рис. 4). В этом случае, при синтезе КИХ-фильтров методом окон, частоты ωС, ωСН, ωСВ могут быть найдены с использованием следующих формул:
Значение величины АЧХ, на частотах среза ωС, ωСН, ωСВ, у фильтров, синтезированных с использованием метода окон, составляет в логарифмическом масштабе -6 дБ. Диаграммы требований к АЧХ фильтров показаны на рис. 4.
Фильтр нижних частот (low- pass filter) Реальный ФНЧ имеет три частотные полосы (рис. 4а): полосу пропускания (ПП), переходную полосу, и полосу задерживания (ПЗ) или иначе ослабления. Коэффициент передачи в полосе пропускания H1, обычно равен 1. Полоса пропускания ограничивается граничной частотой в ПП ωП; ширина ПП DωПП = ωП; dП – максимальное отклонение АЧХ от желаемой (в единицах коэффициента передачи) в ПП, часто выражаемое в дБ с использованием величины R, получившей название максимально допустимого затухания в ПП (неравномерность в ПП):
Переходная полоса располагается между полосами пропускания и задерживания; ширина переходной полосы Dω = ωЗ.- ωП. Поскольку в этой полосе требования не задаются, удовлетворительным окажется любое решение, если оно соответствует требованиям в полосах пропускания и задерживания. Полоса задерживания (ослабления) лежит в пределах от граничной частоты в ПЗ ωЗ до половины частоты дискретизации ωД/2; ширина ПЗ DωПЗ = ωД/2 — ωЗ; dЗ – отклонение АЧХ от 0 в ПЗ, часто выражаемое в дБ с использованием величины A, получившей название минимально допустимого затухания в ПЗ (затухание в ПЗ):
Фильтр верхних частот (high-pass filter) Реальный ФВЧ имеет, как и ФНЧ, три частотных полосы, которые расположены в обратном, относительно ФНЧ, порядке (рис. 4б). Полоса задерживания лежит в пределах от 0 до ωЗ; ширина ПЗ DωПЗ = ωЗ. Переходная полоса лежит в пределах от ωЗ до ωП; ширина переходной полосы Dω = ωП — ωЗ. Полоса пропускания лежит в пределах от ωП до ωД/2; ширина ПП DωПП = ωД/2 — ωП. Полосовой фильтр (band-pass filter) Реальный ПФ характеризуется пятью частотными полосами (рис. 4в), из которых одна – центральная – полоса пропускания, две полосы задерживания и две переходные полосы. Обозначения, приведенные на рис. 4в, следующие: ωЗН – граничная частота первой полосы задерживания (ПЗ1); ширина ПЗ1 DωПЗ1 = ωЗН; ωПН – нижняя граничная частота ПП; ωПВ – верхняя граничная частота ПП; ширина ПП DωПП = ωПВ — ωПН; ωЗВ – граничная частота второй полосы задерживания (ПЗ2); ширина ПЗ2 DωПЗ2 = ωД/2 — ωЗВ. Переходные полосы 1 и 2 имеют ширину Dω1 = ωПН — ωЗН и Dω2 = ωЗВ — ωПВ. Заграждающий (режекторный) фильтр (band-stop filter) Реальный ЗФ (иногда называют полосно-заграждающим), подобно ПФ характеризуется пятью полосами (рис. 4г), из которых две полосы пропускания, одна полоса задерживания и две переходные полосы. Обозначения, приведенные на рис. 4г, следующие: ωПН – граничная частота первой полосы пропускания (ПП1); ширина ПП1 DωПП1 = ωПН; ωЗН – нижняя граничная частота ПЗ; ωЗВ – верхняя граничная частота ПЗ; ширина ПЗ DωПЗ = ωЗВ — ωЗН; ωПВ – граничная частота второй полосы пропускания (ПП2); ширина ПП2 DωПП2 = ωД/2 — ωПВ. Синтез нерекурсивных КИХ-фильтров Если исходными данными для проектирования является именно импульсная характеристика фильтра, то проектирование не требует вообще никаких усилий. Обычно, однако, исходными данными является требуемая амплитудно-частотная характеристика фильтра (АЧХ) H(ω). Синтез НРФ состоит в определении импульсной характеристики фильтра h[k], обеспечивающей выполнение требований, предъявляемых к фильтру. Обычно эти требования задаются в виде желаемых частотных характеристик. Импульсная характеристика h[k] НРФ является конечной и определяется для значений k, лежащих в диапазоне [0, N-1]. Синтез НРФ предусматривает выполнение следующих основных этапов: 1) определение числа коэффициентов фильтра N (порядка фильтра); 2) выбор метода синтеза (метода аппроксимации), минимизирующего отклонение между желаемыми и реальными характеристиками фильтров; 3) вычисление коэффициентов НРФ в соответствии с выбранным методом. Напомним, что для НРФ коэффициенты фильтра b[k] равны отсчетам импульсной характеристики h[k]; 4) анализ результатов синтеза и принятие решений относительно свойств синтезированного фильтра. Если результаты синтеза не удовлетворяют заданным требованиям, то выполняют повторный синтез при других значениях N или выбирают другой метод синтеза. Импульсная характеристика КИХ-фильтров с линейной фазой Поскольку частотная характеристика любого идеального цифрового фильтра H(e j ω ) является периодической функцией частоты с периодом T0 частоты дискретизации ωд, то она связана с импульсной характеристикой h[n] парой дискретно-непрерывных преобразований Фурье (ДНПФ):
Тогда, нормируя частоту по (2а), выражения (6) можно переписать (с учетом T0·dω = dT0ω = dw и изменения пределов интегрирования на интервал от -π до +π)
Ясно, что это – физически нереализуемый БИХ-фильтр, поскольку импульсная характеристика бесконечна и при n j w ) = ±| H(e j w )|·e j (β — αw) . В [2] показано, что в этом случае
Фильтры, удовлетворяющие условиям 14-16, снова создают задержку в (N-1)/2 интервалов дискретизации, но их импульсные характеристики в отличие от предыдущего случая антисимметричны относительно центра. Как и в предыдущем случае, возможны 2 варианта импульсных характеристик: для фильтров с нечетным и четным N. Следует отметить, что для нечетных значений N, согласно (16), h[(N — 1)/2] = 0. Условия 14 – 16 используются при расчете широкополосных дифференциаторов и преобразователей Гильберта. Итак, в зависимости от значения N (нечетные или четные) и вида симметрии импульсной характеристики (симметричная или антисимметричная характеристика) возможны четыре различных вида КИХ-фильтров с линейными фазовыми характеристиками: 1) N — нечетное и коэффициенты симметричны h[n] = h [N – 1 — n]; 2) N — четное и коэффициенты симметричны h [n] = h [N – 1 — n]; 3) N — нечетное и коэффициенты антисимметричны h [n] = — h [N – 1 — n]; 4) N — четное и коэффициенты антисимметричны h [n] = — h [N – 1 — n]. Частотная характеристика КИХ-фильтров с линейной фазой Выразим функцию H(e j ω ) через значения коэффициентов импульсной характеристики. Рассмотрим сначала некаузальный НРФ с симметричной импульсной характеристикой
Частотная характеристика такого фильтра (10) запишется в виде
где a[n] = 2hНК[n] кроме a[0] = hНК[0]. Таким образом, частотная характеристика некаузального НРФ является действительной функцией и характеризуется нулевым сдвигом фазы. Импульсная характеристика каузального НРФ первого вида может быть получена из (18) путем задержки на K=(N-1)/2 тактов. В частотной области эта задержка соответствует сдвигу фазы, определяемому множителем
Множитель Для фильтров второго вида с симметричной h[n] и четным N в выражение для частотной характеристики необходимо дополнительно внести задержку на половину такта и вместо функций cos(nw) использовать функции cos(n+0,5)w [2]:
Необходимо отметить, что H2(w) = 0 при w = π и независимо от значений h[n]. Отсюда следует, что нельзя использовать фильтры этого вида для аппроксимации частотной характеристики, отличной от нуля при w = π (например, при проектировании фильтров верхних частот или режекторных фильтров). Для фильтров третьего вида с антисимметричной h[n] и нечетным N выражение, определяющее частотную характеристику, почти аналогично (16), но вместо cos(nw) необходимо подставить sin(nw) и учесть дополнительный сдвиг на π/2 согласно (15) [2]:
Видно, что H3(w)=0 на частотах w = 0 и w = π; независимо от значений h[n]. Более того, множитель e j π /2 = j в формуле (20) показывает, что без учета множителя с линейным изменением фазы частотная характеристика является чисто мнимой функцией. Поэтому этот вид фильтров наиболее пригоден для проектирования преобразователей Гильберта и дифференциаторов. Для фильтров четвертого вида с антисимметричной h[n] и четным N выражение для частотной характеристики аналогично для фильтров второго типа с заменой косинусов на синус [2]
причем H4(w)=0 на частотах w = 0. Следовательно, этот вид фильтров наиболее пригоден для проектирования преобразователей Гильберта и дифференциаторов. Методы расчета КИХ-фильтров с линейными фазами Известны три класса методов проектирования КИХ-фильтров с линейной фазой: методы взвешивания с помощью окна, методы частотной выборки и проектирование оптимальных (по Чебышеву) фильтров с минимаксной ошибкой. Все они имеет свои достоинства и недостатки, выбор метода проектирования определяется большим числом факторов и в каждом конкретном случае выбирается индивидуально. Метод взвешивания (метод окон) Основное достоинство метода взвешивания заключается в его простоте и легкости использования, во многом базирующиеся на том, что почти всегда можно найти замкнутые выражения для вычисления коэффициентов фильтра с использованием формул дискретно-непрерывного преобразования Фурье (6). Когда же характеристика H(e j ω ) имеет сложный вид или не может быть просто преобразована в замкнутое математическое выражение (а иногда и в случае, когда это возможно), формула (6) зачастую оказывается громоздкой или неудобной для интегрирования. В этом случае использование метода окон проблематично. Однако замена интегрирования в (6) на суммирование с большим числом членов [2] уменьшает значение этого недостатка. Другой недостаток метода взвешивания заключается в отсутствии достаточной гибкости при выполнении проектирования. Например, при расчете фильтра нижних частот трудно, как правило, точно определить граничную частоту полосы пропускания, поскольку окно «размывает» разрыв идеальной характеристики. Результирующая характеристика имеет две граничные частоты — ωП для полосы пропускания и ωЗ для полосы задерживания. И хотя при разработке фильтров типа идеального фильтра нижних частот эффекты размытия удается скомпенсировать, для фильтров с более сложными характеристиками этого достичь непросто [2]. Т.е. метод взвешивания не является оптимальным в том смысле, что он не позволяет получить минимально возможные пульсации для заданного порядка фильтра N и заданного множества частот среза. Еще одной особенностью, которая может препятствовать использованию метода взвешивания, является то, что для частотно-избирательных фильтров одинаково аппроксимируются переходные полосы и пульсации в полосе пропускания и полосе задерживания. Рассмотренная ранее операция усечения (рис. 3) и (10) с точки зрения импульсной характеристики h[n] представляет собой умножение ее на последовательность v[n] (на прямоугольное весовое окно) длиной N отсчетов вида:
в зависимости от того, усекаем мы вначале импульсную характеристику или сдвигаем (далее будем рассматривать смещенные окна при 0 ≤ n ≤ N – 1 (рис. 7)), т.е.
Синтезированный таким образом НРФ будет иметь значительные пульсации АЧХ в районе частоты среза (рис.8). Это явление получило название «эффект Гиббса». Размах пульсаций вблизи точки разрыва максимален слева и справа, составляет 9% от АЧХ и остается таким вне зависимости от N.
Частотная характеристика, соответствующая умножению заданной импульсной характеристики на прямоугольное окно (28), будет равна свертке заданной частотной характеристики с частотной характеристикой прямоугольного окна
где * — символ свертки; θ — переменная интегрирования;
Функция (30) известна под названием ядра Дирихле. Если не учитывать множитель
будет иметь форму, показанную на рис. 9, а ее модуль в области положительных частот — на рис. 10.
Это быстроколеблющаяся функция с максимальным значением N при w = 0, резко спадающая по амплитуде. Область с максимальной амплитудой называется главным лепестком, а остальные области — боковыми лепестками.
Функция V(jw) принимает нулевые значения на частотах w=2πk/N, k=1,2,…,N-1, а ширина всех лепестков, включая главный, одинакова и равна
причем с увеличением N ширина главного лепестка уменьшается и увеличивается число пульсаций. Иногда ширина главного лепестка выбирается вдвое больше той, которая определяется с использованием выражения (31). Последнее связано с тем, что главный лепесток модуля частотной характеристики окна математически определен как в положительной, так и в отрицательной области частот. Таким образом, эффект Гиббса связан с пульсирующим поведением частотной характеристики прямоугольного весового окна. Для уменьшения отрицательного влияния эффекта Гиббса применяют весовые окна, отличные от прямоугольного. С целью обеспечения линейности ФЧХ указанные оконные функции должны быть симметричными
Метод синтеза передаточной функции с помощью ограничения ряда (6) окном (32) называется методом окон или взвешивания. За счет выбора формы окна и его длины можно осуществить некоторое управление процессом расчета. Форма окна является существенной при определении минимального ослабления в полосе задерживания. Можно сформулировать следующие требования к весовой функции окна, которая должна иметь: — минимальную ширину главного лепестка ΔωГЛ: — минимальный уровень боковых лепестков dБЛmax и минимальную площадь под боковыми лепестками; — минимальную длину N. Требования эти достаточно противоречивы. Так, более гладкие весовые функции имеют меньший уровень боковых лепестков, но большую ширину главного лепестка, уменьшающуюся с увеличением длины весовой функции N. Этим объясняется многообразие используемых на практике типов весовых функций, применение которых определяется характером поставленной задачи синтеза фильтров. Кроме прямоугольного окна чаще всего рассматривают обобщенное окно Хэмминга и окно Кайзера. Параметры и математические описания некоторых из оконных функций приведены в Приложении. Стратегия выбора окна диктуется компромиссом между смещением из-за помех в области близких боковых лепестков и смещением из-за помех в области дальних боковых лепестков. Например, если достаточно сильные компоненты помехи расположены вблизи и на отдалении от слабой компоненты сигнала, то следует выбирать окно с одинаковым уровнем боковых лепестков около главного лепестка, с тем чтобы обеспечить малое смещение; см. рис. 11, а.
Если же имеется одна сильная компонента помехи, удаленная от слабой компоненты сигнала, как доказано на рис. 11, б, то следует выбирать окно с быстро спадающим уровнем боковых лепестков, причем их уровень в непосредственной близости к главному лепестку в данном случае не имеет большого значения. В том случае, когда необходимо обеспечить высокое разрешение между очень близкими компонентами сигнала и помехи, а удаленные компоненты отсутствуют, вполне приемлемым может оказаться окно даже с увеличивающимся уровнем боковых лепестков, но зато с очень узким главным лепестком, что иллюстрирует рис. 11, в. Если динамический диапазон сигнала ограничен, то характеристики боковых лепестков не имеют особого значения, и поэтому можно выбрать окно, которое проще для численной реализации. Если спектр сигнала относительно гладок, то можно вообще не применять окна. Окна, которые могут сами в некотором смысле регулироваться, или «адаптироваться», к параметрам данных. Методика синтеза НРФ методом весовых функций [5] 1. Если частота среза и ширина переходной полосы не заданы напрямую, необходимо по значениям граничных частот полос пропускания/подавления рассчитать частоты среза по (3). В качестве частот среза заданной частотной характеристики используют их расчетные значения ωс, смещенные в полосу задерживания примерно на половину переходной полосы фильтра Δωпер. Это связано со свойственным данному методу размыванием границ перехода от полосы пропускания фильтра к полосе задерживания. 2. Если затухание частотной характеристики в полосе задерживания (максимальная неравномерность АЧХ в полосе подавления δ2) задана в долях коэффициента передачи, то по (5) пересчитать ее в логарифмический масштаб. 3. Определить, если не задана, ширину переходной полосы Dωпер = |ωЗ — ωП|min. 4. По полученному (заданному) значению затухания частотной характеристики в полосе задерживания A с помощью табл. П3, П4 или П5 Приложения выбирается тип весовой функции, отвечающей условию |δ2max |, дБ ≥ A, дБ, при минимальном значении ширины ее главного лепестка, т. е. параметра D. При использовании весовой функции Кайзера по табл. П6 Приложения находятся соответствующие заданному затуханию A параметры данной весовой функции β и D. При этом нужно учитывать, что расчетное значение затухания зависит от вида АЧХ синтезируемого фильтра, его граничных частот и длины весовой функции N и может оказаться как больше, так и меньше оценочного значения δ2max. Чем сложнее АЧХ фильтра (ПФ, ЗФ, многополосный фильтр (МПФ)), тем меньше затухание для одной и той же весовой функции. Это же относится и к неравномерности АЧХ в полосе пропускания. 5. Для выбранной (или заданной) весовой функции и рассчитанной (заданной) переходной полосе частотной характеристики фильтра Dωпер в соответствии с приближенным соотношением ΔωГЛ = Dωпер = Dωд/N (ΔωГЛ — ширина главного лепестка спектральной плотности) определяется порядок фильтра (длина весовой функции/длина импульсной характеристики фильтра): где D – коэффициент (D-фактор), зависящий от типа весовой функции (см. табл. П4 – П6 Приложения). Значение N приравнивается ближайшему целому числу, обычно нечетному. 6. С помощью обратного преобразования Фурье 7. Находится импульсная характеристика фильтра путем весового усечения смещенной вправо на (N − 1)/2 отсчетов импульсной характеристики h[k] путем умножения на функцию окна v[n] (весовую функцию) (см. Приложение 2): 8. Рассчитывается АЧХ фильтра 9. Так как данный метод не обеспечивает точного соответствия исходных и расчетных данных (является итерационным), при необходимости корректируются значения расчетных частот среза ωС и порядка фильтра N и расчеты повторяются. 10. Находится минимально необходимая разрядность значений импульсной характеристики h[n] (коэффициентов фильтра, реализуемого на основе дискретной свертки), при которой расчетная АЧХ еще удовлетворяет заданным требованиям. 11. Выбирается способ реализации НРФ (дискретной свертки, ДПФ или частотной выборки) и решаются соответствующие ему задачи реализации. Следует отметить, что метод весовых функций обеспечивает строгую линейность ФЧХ и постоянство группового времени запаздывания фильтра ввиду четной или нечетной симметрии получаемой этим методом импульсной характеристики h[n] = h[N — l — n]. Рассмотрим сначала применение описанной методики для синтеза нерекурсивных ФНЧ, а затем распространим полученные результаты на синтез остальных нерекурсивных фильтров. Заданная частотная характеристика идеального цифрового ФНЧ (рис. 1 а) определяется соотношением
Используя разложение в ряд Фурье частотной характеристики (33), определим импульсную характеристику НРФ
Учитывая, что HЗ(ω) является четной функцией частоты перепишем (34) в виде
Для ФНЧ после подстановки (33) в (35) и выполнения интегрирования получаем
Импульсная характеристика (36) определена при любых, целых значениях n и является бесконечной. Физически реализуемый НРФ обладает конечной импульсной характеристикой. Поэтому необходимо ограничить значения n. Пусть | n | ≤ K, где K = (N-1)/2 для фильтров с нечетными значениями N и K = N/2 для фильтров с четными значениями N. Тогда импульсная характеристика, соответствующая (36), запишется в виде
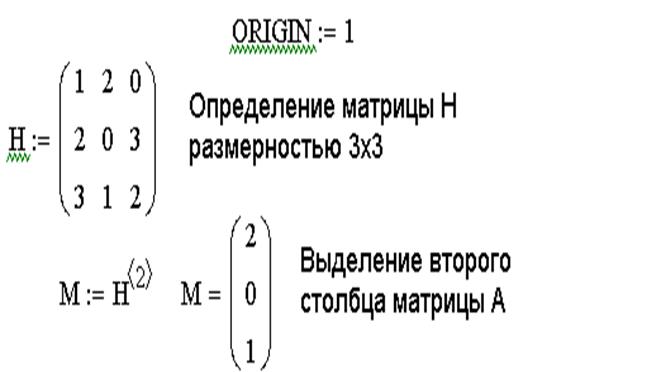
Импульсная характеристика (37) является некаузальной, так как имеет ненулевые значения при n Видео:Основные действия с матрицами и векторами в MathCAD 14 (20/34)Скачать  Векторы и матрицы в MathСadВы уже наверняка не раз сталкивались с такими понятиями как векторы и матрицы. Вектор – это обыкновенный столбец с числами. Матрица представляет собой сборный блок с объектами. Именно на работе с этими элементами построен принцип функционирования программы Excel. В этом уроке мы расскажем о том, как работать с такими вычислениями в программе Маткад и акцентируем внимание на том, почему процесс работы в данном ПО куда проще и удобнее. Мы уже рассказывали в своих уроках о том, что все наши векторы начинались с элемента с нулевым значением. Сейчас же мы поставим номером первого элемента цифру один, ведь так нам гораздо проще будет сориентироваться в учебном материале.
Данное значение можно внести прямо в рабочее поле.
Посмотрите на матрицы на рисунке ниже.
Как вы можете заметить, в них входят и числа, и функции. Помимо этого, сюда можно внести и текст. Чтобы вывести элемент матрицы, воспользуйтесь подстрочным индексом.
Матрицы, описанные на скрине повыше, относятся к квадратному типу. Тем не менее, пользователь может самостоятельно устанавливать их размерные рамки.
Примите во внимание, что первое число обозначает общую нумерацию строчки, а второе – номер столбика.
Для векторного столбца второй индекс можно удалить. Для строки же он является обязательным.
Нужные команды, для всевозможного выделения строчек или столбиков вы всегда сможете отыскать во вкладке «Математика».
Большинство операций для векторных и матричных конструкций вполне соответствуют работе со стандартными числами и функциями. Для того, чтобы отыскать обратную матрицу, потребуется действовать по аналогии с операциями деления. Пользователь может записать операторы, задав им наименования матриц и векторов. Например, это может выглядеть так:
Более подробно мы рассмотрим данный опционал немного погодя. Стоит отметить, что такая функция нуждается в девяти операциях умножения и в таком же количестве деления. Согласитесь, что расписывать все эти процессы достаточно скучно. К тому же, с большими матрицами такой подход нерациональный. Методика применения векторов отличается значительным разнообразием. Чтобы разработать вектор или матрицу, понадобится открыть вкладку «Вставить матрицу». На экране появится сетка с изображением маленьких квадратиков.
Перемещаем указатель на эту сетку. Настраиваем курсор на нужные габариты матрицы. Кликаем дважды ЛКМ. На экране появляется новая матрица.
Матрица может быть переименована, после того, как пользователь дважды кликнет по левой скобке.
Чтобы быстро вставить или удалить строчки да столбцы, можно вызвать контекстное меню «Операторы с векторамиматрицами» на одноименной вкладке.
Работа с матрицамиЭффекты от матриц или вектором гораздо проще сообразить, пользуясь специально разработанными символами. Обратите внимание на скрин ниже.
Оператор транспортировки вызывается посредством выполнения операции Математика –> Операторы –> Векторы и матрицы:
Кликаем по правой стороне матрицы и применяем оператор. Он подходит как для символьных, так и численных матриц.
Операции в векторах часто выполняются по одному элементу. В этой ситуации можно воспользоваться очень удобным оператором, который отвечает за разработку вектора. Чтобы перемножить два вектора, понадобится выполнить простой пример.
Теперь нам нужно выбрать нужные параметры и активировать векторизацию.
Вычисляем заданные параметры и смотрим на результат. Первый элемент приумножился на второй, и так далее.
Еще примеры таких опций.
Операции поэлементного типа могут применяться исключительно к массивам одинакового размера. Добавление и вычитаниеДанные операции относятся к поэлементному типу.
Она также применяется к массивам одинакового размерного типа. Пользуясь оператором, предназначенным для суммирования, можно отыскать сумму всех векторных частей.
Скалярное произведение работает по представленному ниже принципу.
При таком типе умножения матриц, программа занимается умножением данных элементов по столбцам. Данная операция может применяться исключительно к тем матрицам, которые характеризуются равным количеством строчек и столбцов.
Обратите внимание, что немалая роль отводится поочередности множителей.
Только в редких случаях скалярное произведение может стать коммутативным.
Скаляр двух векторов показывает результат как на фотографии ниже.
Данная опция может использоваться исключительно для двух векторных столбов из трех элементов.
Векторное произведение часто используется для механики, гидродинамики и огромного количества подобных сфер деятельности. Обратная матрица может быть применима для квадратных матриц:
В результате у нас получится матрица единичного типа
Если произвести матрицу и единичную матрицу, мы получим первоначальный вариант.
Определитель может быть разработан исключительно для матрицы квадратного типа. Он может быть нулевым в любых условиях. Обратная матрица имеет в своей структуре дроби, в состав которых входит определитель.
В ситуациях, когда определитель установлен на ноль, к нему нереально подобрать обратную матрицу. Сама матрица автоматически становится сингулярной. О таких изменениях пользователь узнает из оповещения программы.
В ситуациях со скалярами, определитель соответствует их модулям
Команда «определитель» помогает отыскать длину вектора .
Уважаемые пользователи, хотим Вас проинформировать о том, что некоторые антивирусные программы и браузеры ложно срабатывают на дистрибутив программы MediaGet, считая его зараженным. Данный софт не содержит никаких вредоносных программ и вирусов и многие из антивирусов просто Вас предупреждают, что это загрузчик (Downloader). Если хотите избежать подобных проблем, просто добавьте MediaGet в список доверенных программ Вашей антивирусной программы или браузера.
Выбрав нужную версию программы и кликнув ссылку, Вам на компьютер скачивается дистрибутив приложения MediaGet, который будет находиться в папке «Загрузки» для Вашего браузера. Находим этот файл с именем программы и запускаем его. И видим первый этап установки. Нажимаем унопку «Далее»
Далее Вам предлагается прочитать и одобрить лицензионное соглашение. Нажимаем кнопку «Принимаю»
В следующем окне Вам предлагается бесплатное полезное дополнительное программоное обеспечение, будь то антивирус или бразуер. Нажимаем кнопку «Принимаю». Также Вы можете отказаться от установки дополнительного ПО, нажав кнопку «Отклоняю»
Далее происходит процесс установки программы. Вам нужно выбрать папку, в которую будут скачиваться нужные Вам файлы.
Происходит завершение установки. Программа автоматически открывается и скачивает нужные Вам исходные файлы. Обратите внимание, что предоставляемое программное обеспечение выкладывается исключительно для личного использования и ознакомления. Все файлы, доступные для скачивания, не содержат вирусов и вредоносных программ. 📸 ВидеоСвертка двух функций. Найти свертку функций по определению. Теорема об умножении изображений.Скачать  Функции для работы с матрицами и векторами в MathCAD 14 (21/34)Скачать  Интеграл свёртки: вывод формулы и её смыслСкачать  Основы ЦОС: 20. Дискретная свёртка (ссылки на скачивание скрипта в описании)Скачать  MathCad компланарность векторов.wmvСкачать  Оператор векторизации в MathCAD 14 (23/34)Скачать  Что такое свёртка списка? Душкин объяснитСкачать  Создание матриц в MathCAD 14 (18/34)Скачать  Векторная диаграмма токов в программе MathcadСкачать  КАК РАЗОБРАТЬСЯ В ВЫСШЕЙ МАТЕМАТИКЕСкачать  МАТКАД МатрицыСкачать  Матрицы в Mathcad(создание и редактирование матриц)(Урок 3.1)Скачать  Матан за час. Шпаргалка для первокурсника. Высшая математикаСкачать  Операции над матрицами в Mathcad(сложение, вычитание, умножение и т.д.)(Урок 3.2)Скачать  О корреляционной функции и её аналитическом вычисленииСкачать  |
, 
, 
.
.
.
, 
,
.
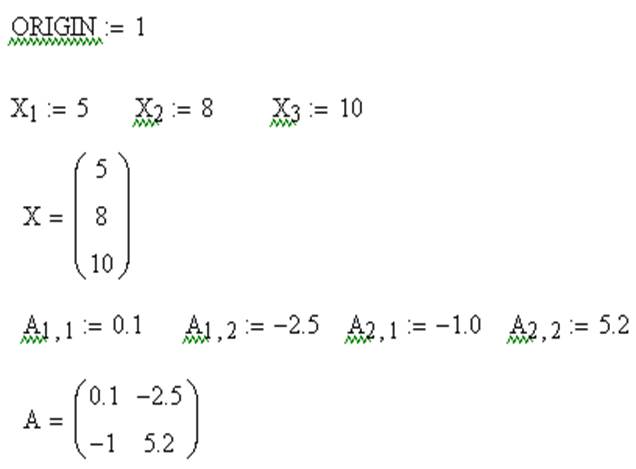
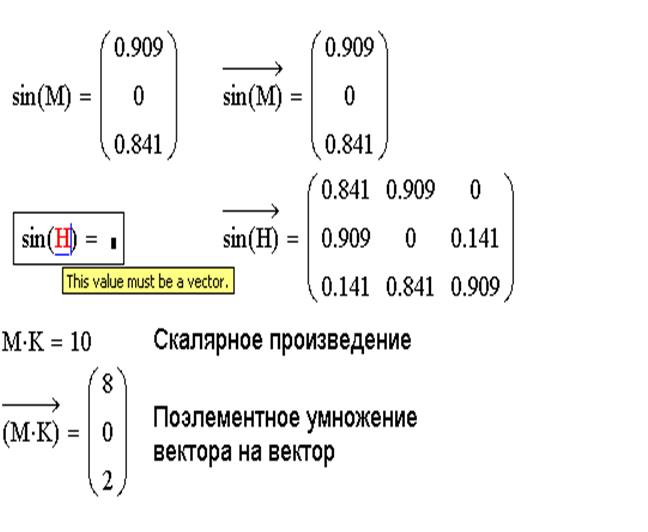
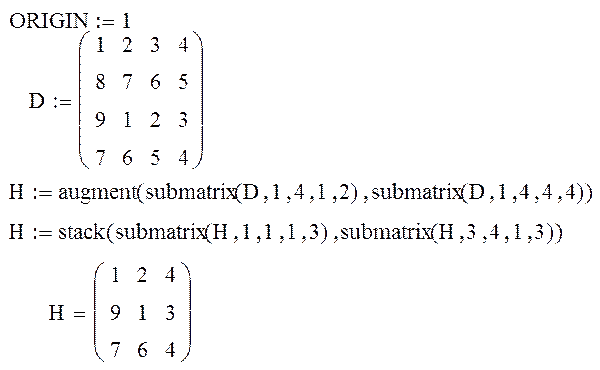
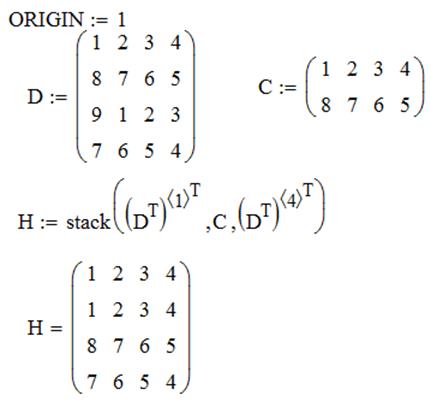
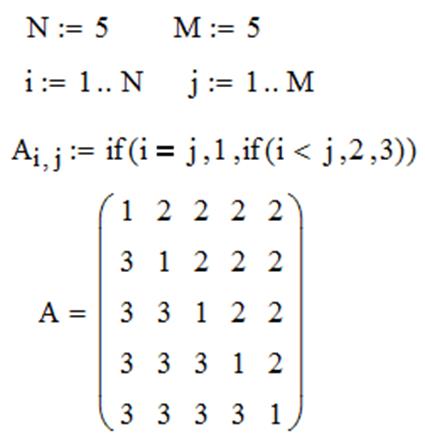
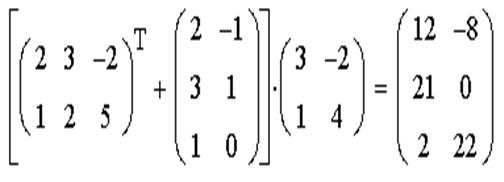
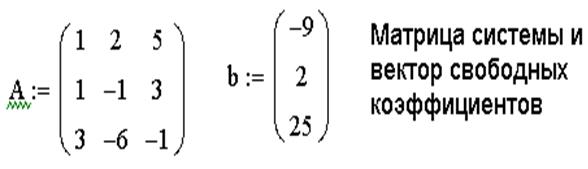
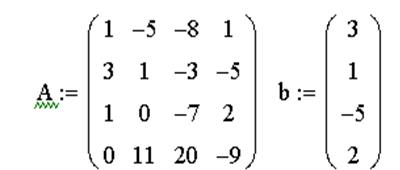
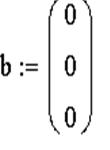
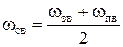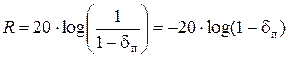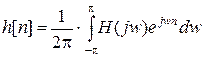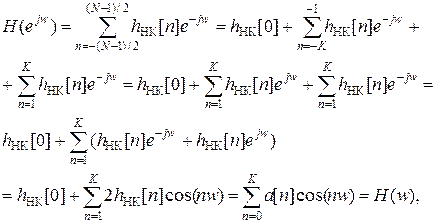
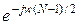. Поэтому частотная характеристика НРФ первого вида запишется в виде
,
,
,
,
,
,
,
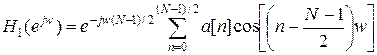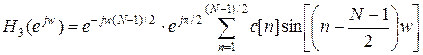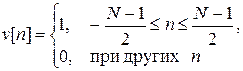
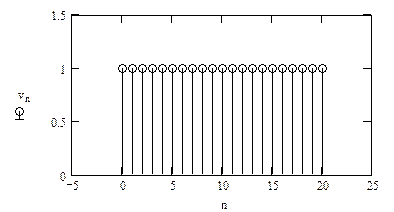
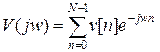— частотная характеристика весовой функции, в данном случае прямоугольного:
,
, характеризующий линейный фазовый сдвиг, то график функции
или по более удобной формуле 
и проверяется ее соответствие исходным данным по неравномерности частотной характеристики в полосе пропускания R и затуханию в полосе задерживания A.
.
.
.
