Калькулятор золотого сечения треугольника (6 видео)

Калькулятор «золотого сечения»

Золотое сечение или Божественная Пропорция были тщательно изучены греческим скульптором и архитектором Фидием. Созданное самой природой правило принято обозначать в честь его открывателя буквой Ф. Фи может быть обнаружено по всей вселенной — от спиралей галактик до спирали раковины Наутилуса. В геометрии золотое сечение можно представить как отрезок C состоящий из двух неравных частей. При этом его меньшая часть A составляет такую же долю в большем отрезке B , как и больший отрезок B занимает во всем отрезке C . В математическом виде правило выглядит так:

Введите один из известных размеров и калькулятор золотого сечения вычислит остальные:

Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!

Содержание

Калькулятор золотого сечения
История
Число Фи в математике
Число Фи в реальности
Калькулятор золотого сечения
Пример из реальной жизни
Живопись
Заключение
Золотое сечение
Золотое сечение
📽️ Видео

Видео:Золотое сечение Принцип построения простыми словамиСкачать

Калькулятор золотого сечения

Золотое сечение — это особое соотношение сторон фигуры, которое наиболее приятно для созерцания. Это число известно с античных времен, а ученые эпохи Возрождения называли его божественной пропорцией. Число Фи — золотое сечение, приблизительно равное 1,618.

Видео:Золотой треугольникСкачать

История

Особую красоту деления отрезка на стороны в соотношении 1/1,618 заметили еще античные ученые. Евклид в своих началах использовал этот метод при построении пентагона, а пифогорейцы рассматривали весь мир как царство математической гармонии и уделяли большое внимание соотношению 1/1,618. В 1202 году Леонардо Фибоначчи вывел особую последовательность, отношение членов которой стремилось к числу Фибоначчи. Лука Пачоли, один из величайших алгебраистов Италии, назвал это соотношение божественной пропорцией, связав свойства бога с числом Фи. Именно с этого момента золотое сечение начало активно использоваться в работах художников эпохи Возрождения и получило буквально мистический статус. По словам Кеплера, число Фи — бесценная жемчужина математики.

Видео:Золотой треугольник | Олимпиадная математикаСкачать

Число Фи в математике

Золотое сечение часто встречается в геометрии. Золотой прямоугольник — фигура на плоскости, длина и ширина которой соотносятся как 1/1,618. Примечательное свойство такого прямоугольника состоит в том, что при удалении из фигуры любого квадрата образуется новый прямоугольник с точно таким же соотношением сторон. Стоит упомянуть и пентаграмму — звездчатый многоугольник, стороны которого пересекаются в соответствии с правилом золотого сечения.

В арифметике число Фи встречается в упоминаемой выше последовательности Фибоначчи, так как lim(Fn/Fn-1) -> Фи. Кроме того, золотое сечение имеет интересное представление в других формах записи. Так, Фи представляется как бесконечная цепочка квадратных корней из единицы. А если привести Фи к цепному виду, то получится бесконечная дробь вида [1; 1, 1, 1, 1, 1…]

Видео:Число Фибоначчи = 1.618. Объяснение математического смысла золотого сеченияСкачать

Число Фи в реальности

Мистический ореол вокруг золотого сечения возник благодаря такому явлению как «золотой числизм». Энтузиасты, задавшиеся целью найти эту пропорцию в как можно большем количестве реальных объектов или явлений, часто подгоняли результаты. К примеру, храм Парфенон всегда присутствует в списке объектов, которые построены с учетом божественной пропорции. Однако на деле соотношение ширины храма к его высоте составляет 1,74, а если исключить фронтон, то и вовсе 3.

После придания числу божественных свойств, многие художники и музыканты начали сознательно использовать это соотношение в своих работах. Леонардо да Винчи, Альбрехт Дюрер, Иоганн Бах, Ле Корбюзье, Густав Фехнер намеренно придавали своим произведениям форму, соответствующую числу Фи. Одним из современных примеров использования золотого сечения является мозаика Пенроуза — метод непериодического разбиения плоскости.

Несмотря на явное преувеличение свойств золотой пропорции, она все же встречается в реальности. Большинство спиралевидных объектов связны с числом Фи: раковины моллюсков, атмосферные вихри и даже галактики действительно соответствуют божественной пропорции.

Видео:Вас обманывают насчет ЗОЛОТОГО СЕЧЕНИЯ!Скачать

Калькулятор золотого сечения

Если вы хотите использовать божественную пропорцию в своей работе, то наш калькулятор к вашим услугам. Для определения сторон золотого прямоугольника вам понадобится ввести одну из сторон, а программа определит вторую, соответствующую правилу золотого сечения. Прелесть калькулятора состоит в том, что он не просто умножает сторону на 1,618, а подбирает целое значение. Именно поэтому вам потребуется оперировать целыми числами, что удобно на практике.

Видео:Что такое золотое сечение? Как использовать золотую спираль в дизайне логотипа? Числа ФибоначчиСкачать

Пример из реальной жизни

Живопись

Допустим, вы хотите сделать приятную с точки зрения математики картину, следовательно, вам нужно нарисовать ее на золотом прямоугольнике. Вам потребуется заказать холст определенного размера, и чтобы определить его размеры, используйте наш калькулятор. Пусть вы хотите писать на холсте, длина которого составит 120 см. Как узнать необходимую ширину? Введите это значение в ячейку A и получите ответ, равный 74 см.

Видео:Числа Фибоначчи и тайна Золотого сеченияСкачать

Заключение

Божественная пропорция — мистическое соотношение, которое занимает умы математиков уже несколько тысячелетий. Возможно, именно число Фи содержит ответы на вечные вопросы о тайнах мироздания. Если вам потребуется создать объекты, соответствующие золотому сечению, используйте наш калькулятор, при помощи которого вы сможете подобрать целые числа.

Видео:Золотое Сечение наглядно - простой способСкачать

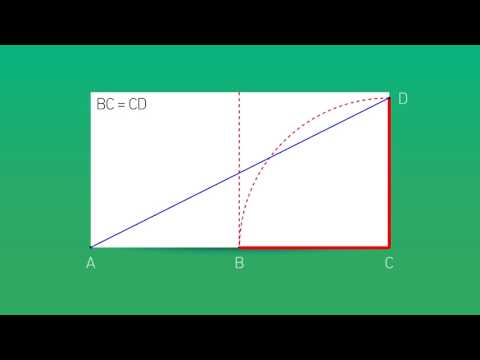
Золотое сечение

Расчет длин отрезков в золотом сечении.

Калькулятор ниже находит параметры, соответствующие золотому сечению. Про само золотое сечение рассказано под калькулятором

Золотое сечение

Золотое сечение — термин, обозначающий деление отрезка на два в соотношении, при котором большая часть относится к меньшей также как весь отрезок относится к большей. Также употребляют термин деление в крайнем и среднем отношении.

Отношение это фиксированное, его можно найти. Представим, что b у нас единица. Тогда значение a должно равняться искомому отношению, и его надо найти — переименуем его в более привычное x и проведем ряд преобразований:

Последнее есть квадратное уравнение. Его положительный корень:

и есть отношение золотого сечения. Число это иррациональное:

Для практических целей иногда используют приближение — большая часть равна 0,62 всей величины, меньшая — 0,38 (это видно, если ввести длину 1, и выбрать тип «суммарный отрезок» в калькуляторе сверху).

Золотое сечение известно еще со времен Евклида (ок. 300 лет до н. э.), и у него много забавных свойств, про которые можно почитать в: Википедии, например, к нему стремится отношение последовательных чисел Фибоначчи.

Для полноты ликбеза скажем, что почему-то считается, что объекты, содержащие золотое сечение, воспринимаются людьми как наиболее гармоничные. Ну а вот целая занятная статья, где золотое сечение находят буквально во всем.