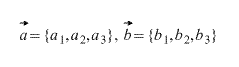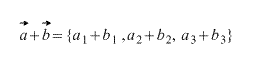Сумма трех векторов из одной точки равна 0

• скалярные величины, задающие некоторое числовое значение — время, температура, масса и т.д.
• векторные величины, которые вместе с некоторым числовым значением задают направление — скорость, сила и т.д..

Рассмотрим сначала алгебраический подход к сложению векторов.

Покоординатное сложение векторов.

Тогда координаты вектора, получившегося при сложении этих двух векторов вычисляются по формуле:

В двумерном случае все абсолютно анологично, просто отбрасываем третью координату.

Теперь перейдем к геометрическому смыслу сложения двух векторов:

При сложении векторов нужно учитывать и их числовые значения, и направления. Есть несколько широко используемых методов сложения:

• правило параллелограмма
• правило треугольника
• тригонометрический способ

Правило параллелограмма. Сложение векторов по правилу параллелограмма.

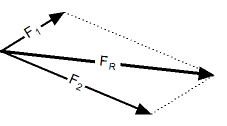Процедура сложения векторов по правилу параллелограмма заключается в следующем: нарисовать первый вектор, учитывая его величину и направление от начала первого вектора нарисовать второй вектор, также используя и его величину, и его направление дополнить рисунок до параллелограмма, считая, что два нарисованных вектора — это его стороны результирующим вектором будет диагональ параллелограмма, причем его начало будет совпадать с началом первого (а, значит, и второго) вектора.

Правило треугольника. Сложение векторов по правилу треугольника.

	Сложение векторов по правилу треугольника заключается в следующем: нарисовать первый вектор, используя данные о его длине ( числовой величине) и направлении от конца первого вектора нарисовать второй вектор, также учитывая и его размер, и его направление результирующим вектором будет вектор, начало которого совпадает с началом первого вектора, а конец — с концом второго.

Тригонометрический способ. Сложение векторов тригонометрическим способом.

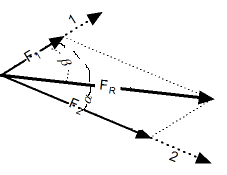Результирующий вектор сложения двух компланарных векторов может быть вычислен с помощью теоремы косинусов: Fрез. = [ F1 2 + F2 2 -2 F1 F2 cos(180 о -α) ] 1/2 (1) где F = числовое значение вектора α = угол между векторами 1 и 2 Угол между результирующим вектором и одним из исходных векторов может быть вычислен по теореме синусов: β = arcsin[ F2 *sin(180 o -α) / FR ] (2) где α = угол между исходными векторами

Пример — сложение векторов.

Сила 1 равна 5кН и воздействует на тело в направлении, на 80 o отличающемся от направления действия второй силы, равной 8 кН.

Результирующая сила вычисляется следующим образом:

F_рез = [ (5 кН) 2 + (8 кН) 2 — 2 (5 кН)(8 kН) cos(180 o — (80 o )) ] 1/2

Угол между результирующей силой и первой силой равен:

А угол между второй и результирующей силой можно посчитать следующим образом: as

α = arcsin [ (5 кН) sin(180 o — (80 o )) / (10,2 кН) ]

Он-лайн калькулятор сложения векторов.

Калькулятор ниже может быть использован для любвых векторных величин ( силы, скорости и т.д.) Точка начала вектора совпадает с началами обоих исходных векторов.

Консультации и техническая
поддержка сайта: Zavarka Team

Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

kak.manesu.com

Видео:8 класс, 45 урок, Сумма нескольких векторовСкачать

§ 2. Сложение векторов.

Известные из механики законы сложения векторных величин (сил, ускорений, скоростей) служат основанием следующего определения сложения векторов. Суммой двух векторов А и В называют такой третий вектор С, выходящий из их общего начала, который служит диагональю параллелограмма, сторонами которого являются слагаемые векторы (рис. 94), и обозначают:

Если два вектора А и В после приведения их к общему началу лежат на одной прямой, то сумма их С есть по определению вектор, длина которого равна сумме длин слагаемых векторов и направление совпадает с направлением этих векторов, если последние одинаково направлены; если же слагаемые векторы направлены в разные стороны, то сумма их С есть вектор, длина которого равна разности длин слагаемых векторов и направление совпадает с направлением вектора, имеющего большую длину. В случае равенства длин противоположно направленных векторов их сумма еегь особый «вектор», длина которого равна нулю. Такой вектор называют нулевым вектором и обозначают символом 0.

Посмотрим теперь, будет ли сложение векторов удовлетворять основным законам, которым подчиняется сложение чисел. Для сложения чисел мы имеем два основных закона.

1. Закон переместительности.

т. е. сумма не зависит от порядка слагаемых.

2. Закон сочетательности:

т. е. чтобы прибавить сумму, можно прибавить последовательно каждое слагаемое.

Первый закон, очевидно, удовлетворяется, что непосредственно вытекает из определения сложения векторов:

Чтобы перейти ко второму закону (сочетательности), следует предварительно выяснить понятие суммы нескольких слагаемых.

С этой целью упростим сначала самое построение суммы двух векторов. Мы условились считать равными векторы, имеющие одинаковую длину, параллельные и одинаково направленные. В силу этого векторы ОВ и АС (рис. 94) равны между собой. Отсюда вытекает такое правило сложения двух векторов: в конце первого слагаемого строим второе слагаемое. Вектор, замыкающий эту ломаную, есть сумма. Начало его совпадает с началом первого слагаемого, а конец — с концом второго.

Это правило треугольника нетрудно теперь распространить на любое число слагаемых. Пусть, например, требуется найти сумму трех векторов А, В и С:

причем под их суммой мы будем подразумевать результат последовательного прибавления к А сначала В и затем С. Другими словами, если

то согласно определению будет:

По предыдущему правилу треугольника строим сначала сумму (рис. 95), т. е. в точке строим вектор и соединяем

точку О с точкой Затем к полученной сумме прибавляем вектор С, т. е. в конце ОЕ строим вектор ED — Q, и соединяем точку О с точкой

Отсюда вытекает такое правило сложения векторов: чтобы построить сумму любого числа векторов, нужно в конце первого слагаемого вектора построить второй, в конце второго построить третий и т. д. Вектор, замыкающий полученную ломаную линию, представляет искомую сумму. Начало его совпадает с началом первого слагаемого, а конец — с концом последнего.

В случае сложения трех векторов, не параллельных одной плоскости, сумму их можно получить и другим способом. Пусть векторы А, В, С приведены к общему началу .

Построим на этих векторах параллелепипед (рис. 96). По предыдущему правилу

но отрезок OD является диагональю параллелепипеда, таким образом сумма данных векторов равна вектору-диагонали параллелепипеда, ребрами которого являются слагаемые векторы.

Заметим, что если бы слагаемые векторы были параллельны одной плоскости (такие векторы называются компланарными), то мы не могли бы построить на них параллелепипед.

Теперь перейдем к доказательству закона сочетательности:

По правилу сложения векторов (рис. 97)

но тому же вектору OD равна и сумма так как

Итак, равенство (3) доказано.

Из переместительного и сочетательного законов вытекает, что при нахождении суммы любого числа векторов можно складывать данные векторы в произвольном порядке.

Заметим, что по отношению к обычной сумме чисел существуют еще различные законы монотонности — о сравнительной величине слагаемых и суммы, как, например, сумма положительных слагаемых больше каждого из слагаемых. Все эти законы не имеют смысла для суммы векторов, потому что понятия «больше» и «меньше» неприложимы к векторам.

📸 Видео

СУММА ВЕКТОРОВ правило треугольникаСкачать

Сложение векторов. Правило параллелограмма. 9 класс.Скачать

8 класс, 43 урок, Сумма двух векторовСкачать

10 класс, 41 урок, Сумма нескольких векторовСкачать

Вычитание векторов. 9 класс.Скачать

длина суммы трёх единичных векторов, между которыми углы по 60 градусовСкачать

Компланарны ли векторы: a=(2;5;8), b=(1;-3;-7) и c=(0;5;10)?Скачать

Геометрия 9 класс (Урок№2 - Сумма двух векторов. Законы сложения векторов.)Скачать

Геометрия - 9 класс (Урок№1 - Понятие вектора. Равенство векторов)Скачать

Сложение нескольких векторов. Правило многоугольникаСкачать

Физика | Ликбез по векторамСкачать

Координаты точки и координаты вектора 1.Скачать

Скалярное произведение векторов. 9 класс.Скачать