Сумма координат вектора решения (7 видео)

Сложение и вычитание векторов

Содержание

Формулы сложения и вычитания векторов
Формулы сложения и вычитания векторов для плоских задач
Формулы сложения и вычитания векторов для пространчтвенных задач
Формулы сложения и вычитания n -мерных векторов
Примеры задач на сложение и вычитание векторов
Примеры плоских задач на сложение и вычитание векторов
Примеры пространственных задач на сложение и вычитание векторов
Примеры задач на сложение и вычитание векторов с размерностью большей 3
Координаты вектора. Направляющие косинусы
Координаты вектора
Сумма двух векторов, заданных координатами
Умножение вектора на число
Направляющие косинусы
Основное свойство направляющих косинусов
Операции над векторами в прямоугольной системе координат
🎥 Видео

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Формулы сложения и вычитания векторов

Формулы сложения и вычитания векторов для плоских задач

В случае плоской задачи сумму и разность векторов a = < a_x ; a_y > и b = < b_x ; b_y > можно найти, воспользовавшись следующими формулами:

Формулы сложения и вычитания векторов для пространчтвенных задач

В случае пространственной задачи сумму и разность векторов a = < a_x ; a_y ; a_z > и b = < b_x ; b_y ; b_z > можно найти, воспользовавшись следующими формулами:

Формулы сложения и вычитания n -мерных векторов

В случае n -мерного пространства сумму и разность векторов a = < a ₁ ; a ₂ ; . ; a_n > и b = < b ₁ ; b ₂ ; . ; b_n > можно найти, воспользовавшись следующими формулами:

Видео:Координаты вектора. 9 класс.Скачать

Примеры задач на сложение и вычитание векторов

Примеры плоских задач на сложение и вычитание векторов

Примеры пространственных задач на сложение и вычитание векторов

Примеры задач на сложение и вычитание векторов с размерностью большей 3

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Видео:Векторы. Метод координат. Вебинар | МатематикаСкачать

Координаты вектора. Направляющие косинусы

Для решения задач с векторами необходимо определить вектор на плоскости или в пространстве, то есть дать информацию о его направлении и длине.

Видео:Сложение, вычитание, умножение на число векторов через координату. 9 класс.Скачать

Координаты вектора

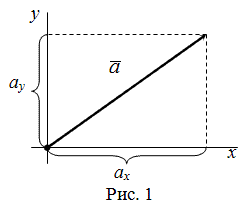
Пусть задана прямоугольная декартова система координат (ПДСК) $x O y$ и произвольный вектор $overline$, начало которого совпадает с началом системы координат (рис. 1).

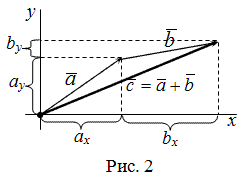
Сумма двух векторов, заданных координатами

Чтобы найти сумму двух векторов, заданных своими координатами, надо сложить их соответствующие координаты.

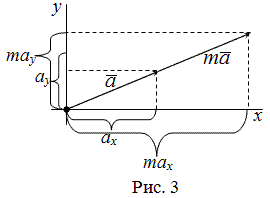
Умножение вектора на число

Чтобы умножить вектор на число, надо каждую координату этого вектора умножить на заданное число.

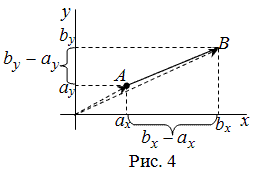
Рассмотрим далее случай, когда начало вектора не совпадает с началом системы координат. Предположим, что в ПДСК заданы две точки $Aleft(a_ ; a_right)$ и $Bleft(b_ ; b_right)$. Тогда координаты вектора $overline=left(x_ ; y_right)$ находятся по формулам (рис. 4):

Чтобы найти координаты вектора, заданного координатами начала и конца, надо от координат конца отнять соответствующие координаты начала.

Задание. Найти координаты вектора $overline $, если $A(-4 ; 2), B(1 ;-3)$

Решение. $overline =(1-(-4) ;-3-2)=(5 ;-5)$

Видео:Координаты вектора в пространстве. 11 класс.Скачать

Направляющие косинусы

Направляющими косинусами вектора называются косинусы углов, образованных вектором с положительными направлениями осей координат.

Направление вектора однозначно задается направляющими косинусами. Для единичного вектора направляющие косинусы равны его координатам.

Здесь $alpha$, $beta$ и $gamma$ — углы, которые составляет вектор с положительными направлениями осей $O x$, $O y$ и $O z$ соответственно.

Основное свойство направляющих косинусов

Сумма квадратов направляющих косинусов равна единице.

Видео:Нахождение координат вектора. Практическая часть. 9 класс.Скачать

Операции над векторами в прямоугольной системе координат

Если задана плоскость O x y с векторами a → = a x , a y и b → = ( b x , b y ) , то мы можем разложить их по координатным векторам i → и j → . Тогда это будет иметь вид a → = a x · i → + a y · j → и b → = b x · i → + b y · j → . Чтобы найти сумму a → и b → и произведение a → на λ , рассмотрим:

a → + b → = a x · i → + a y · j → + b x · i → + b y · j → = ( a x + b x ) · i → + ( a y + b y ) · j →

λ · a → = λ · ( a x · i → + a y · j → ) = ( λ · a x ) · i → + ( λ · a y ) · j →

Это равенство справедливо по свойству операций над векторами.

Разложение векторов – это a → + b → и λ · a → , представленное в частях неравенства по i → и j → координатам. Координаты векторов a → + b → и λ · a → равны соответственно ( a x + b x , a y + b y ) и ( λ · a x , λ · a y ) .

Таким же образом a → = ( a x , a y , a z ) и b → = ( b x , b y , b z ) записываются как a → + b → = a x · i → + a y · j → + a z · k → + b x · i → + b y · j → + b z · k → = ( a x + b x ) · i ⇀ + ( a y + b y ) · j → + ( a z + b z ) · k → λ · a → = λ · ( a x · i → + a y · j → + a z · k → ) = ( λ · a x ) · i → + ( λ · a y ) · j → + ( λ · a z ) · k →

а значит a → + b → = ( a x + b x , a y + b y , a z + b z ) , λ · a → = ( λ · a x , λ · a y , λ · a z )

Отсюда делаем вывод, что координаты векторов a → и b → равны сумме соответствующих координат векторов a → и b → , координаты произведения вектора a → на λ приравниваются к соответствующим координатам вектора a → , умноженным на число в заданной системе координат.

При необходимости нахождения координат суммы нескольких векторов, необходимо сложить координаты каждого вектора соответственно. Рассмотрим примеры.

Нужно выполнить сложение a → = ( 2 , 3 — 1 3 ) и b → = ( — 1 , — 1 3 ) . Чему равны координаты произведения вектора a → на 3 .

Решение

Из определения имеем, что сумма векторов равна сумме их координат соответственно, тогда a → + b → = ( 2 + ( — 1 ) , 3 — 1 3 + ( — 1 3 ) ) = ( 1 , — 1 3 ) .

Числовое значение умножается на каждую координату: 3 · a → = ( 3 · 2 , 3 · 3 — 1 3 ) = 2 3 , 3 — 3 3 .

Ответ: a → + b → = ( 1 , — 1 3 ) , 3 · a → = ( 2 3 , 3 — 3 3 )

Заданы векторы a → = ( 0 , 1 , — 2 ) , b → = ( — 1 , — 1 , 3 ) , c → = ( 4 , — 3 , 2 ) .

Каковы координаты вектора 2 · a → + 3 · ( b → — c → ) = 2 · a → + 3 · b → + ( — 3 ) · c → .

Решение

Применяя свойства векторов, получим: 2 · a → + 3 · ( b → — c → ) = 2 · a → + 3 · b → + ( — 3 ) · c → .

Подставляем значения координат и получаем: 2 · a → + 3 · b → + ( — 3 ) · c → = 2 · ( 0 , 1 , — 2 ) + 3 · ( — 1 , — 1 , 3 ) + ( — 3 ) · ( 4 , — 3 , 2 ) =

= ( 2 · 0 , 2 · 1 , 2 · ( — 2 ) ) + ( 3 · ( — 1 ) , 3 · ( — 1 ) , 3 · 3 ) + ( ( — 3 ) · 4 , ( — 3 ) · ( — 3 ) · 2 ) =

= ( 0 , 2 , — 4 ) + ( — 3 , — 3 , 9 ) + ( — 12 , 9 — 6 ) =

= ( 0 + ( — 3 ) + ( — 12 ) , 2 + ( — 3 ) + 9 , — 4 + 9 + ( — 6 ) ) = ( — 15 , 8 , — 1 )

Можно решить другим способом.

Обратим внимание на разложение a → , b → и c → :

a → = 0 · i → + 1 · j → + ( — 2 ) · k → = j → — 2 · k →

b → = ( — 1 ) · i → + ( — 1 ) · j → + 3 · k → = — i → — j → + 3 · k →

c → = 4 · i → + ( — 3 ) · j → + 2 · k → = 4 · i → — 3 · j → + 2 · k →

Исходя из свойств векторов, видим, что: 2 · a → + 3 · ( b → — c → ) = 2 · ( j → — 2 · k → ) + 3 · ( — i → — j → + 3 · k → — ( 4 · i → — 3 · j → + 2 · k → ) ) = = 2 · j → — 4 · k → + 3 · ( — 5 · i → + 2 · j → + 1 · k → ) = — 15 · i → + 8 · j → — k →

Значит, координаты вектора 2 · a → + 3 · ( b → — c → ) равны ( — 15 , 8 , — 1 ) .

Ответ: 2 · a → + 2 · ( b → — c → ) = ( — 15 , 8 , — 1 )