На стороне ad параллелограмма abcd отложен вектор ak длины ak 1 5 ad

Видео:18+ Математика без Ху!ни. Векторное произведение.Скачать

Nav view search

Navigation

Search

• Вы здесь:
• Home

Видео:№783. Точка М лежит на стороне ВС параллелограмма ABCD, причем ВМ:МС=3:1. ВыразитеСкачать

Линейные комбинации, линейная зависимость векторов. Коллинеарные и компланарные вектора.

Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.

Система векторов $a_1, a_2, . a_n$ называется линейно зависимой, если существуют числа $lambda_1, lambda_2, . lambda_n$ такие, что хотя бы одно из них отлично от нуля и $lambda_1 a_1+lambda_2 a_2+. +lambda_n a_n=0.$ В противном случае система называется линейно независимой.

Два вектора $a_1$ и $a_2$ называются коллинеарными если их направления совпадают или противоположны.

Три вектора $a_1, a_2$ и $a_3$ называются компланарными если они параллельны некоторой плоскости.

Геометрические критерии линейной зависимости:

а) система $$ линейно зависима в том и только том случае, когда векторы $a_1$ и $a_2$ коллинеарны.

б) система $$ линейно зависима в том и только том случае, когда векторы $a_1,, a_2$ и $a_3$ компланарны.

Примеры.

2.19.

Разложить вектор $s=a+b+c$ по трем некомпланарным векторам: $p=a+b-2c,$ $q=a-b,$ $r=2b+3c.$

Решение.

Найдем такие $alpha, beta$ и $gamma,$ что $s=alpha p+beta q+gamma r:$

Из этого равенства, приравнивая коэффициенты при $a, b$ и $c$ получаем систему уравнений: $$left<begin1=alpha+beta\ 1=alpha-beta+2gamma\ 1=-2alpha+3gammaendright.$$

Решим эту систему уравнений методом Крамера:

Таким образом, $s=frac p+frac q+fracr.$

Ответ: $s=frac p+frac q+fracr.$

Доказать, что для любых заданных векторов $а,, b $ и $c$ векторы $a+b,,, b+c,,, c-a$ компланарны.

Доказательство.

Cистемы векторов $; ,,,,, $ являются компланарными поскольку они линейно зависимы: $a+b-(a+b)=0; ,,$ $b+c-(b+c)=0;,,$ $ -c+a+(c-a)=0.$ Отсюда следует, что если вектора $а,, b $ и $c$ компланарны, то векторы $a+b,,, b+c,,, c-a$ также компланарны.

Пусть векторы $a, b$ и $c$ не компланарны.

Так как векторы $a_1,, a_2$ и $a_3$ компланарны в том и только том случае, когда система $$ линейно зависима, то нам нужно показать, что система векторов $a+b,,, b+c,,, c-a$ линейно зависима. Для этого покажем, что существуют числа $alpha,, beta$ и $gamma$ такие, что хотя бы одно из них отлично от нуля и $alpha(a+b)+beta(b+c)+gamma(c-a)=0.$

Предположим противное: вектора $a+b,,, b+c,,, c-a$ некомпланарны. Тогда равенство $alpha(a+b)+beta(b+c)+gamma(c-a)=0$ верно только в случае $alpha=beta=gamma=0$

Запишем последнее уравнение в виде $a(alpha-gamma)+b(alpha+beta)+c(beta+gamma)=0.$ Так как мы рассматриваем случай когда векторы $a, b$ и $c$ некомпланарны, то должны выполняться уравнения

Это вырожденная система: $$begin1&0&-1\1&1&0\0&1&1end=0,$$

поэтому данная система имеет нетривиальное решение, например $alpha=gamma=1;,,beta=-1.$ Получили противоречие.

Таким образом, для любых заданных векторов $а,, b $ и $c$ векторы $a+b,,, b+c,,, c-a$ компланарны. Что и требовалось доказать.

Домашнее заданее.

№2.18

На стороне $AD$ параллелограмма $ABCD$ отложен вектор $overline$ длины $|overline|=1/5|overline|,$ а на диагонали $AC$ вектор $overline$ длины $|overline|=1/6|overline|$ . Доказать, что векторы $overline$ и $overline$ коллинеарны и найти $lambda$ такое, что $overline=lambdaoverline.$

№2.20

Найти линейную зависимость между данными четырьмя некомпланарными векторами: $p=a+b,, q=b-c,,r=a-b+c,, s=b+1/2c.$

Видео:№770. Дан параллелограмм ABCD. Выразите вектор АС через векторы а и b , если:Скачать

В параллелограмме ABCD К ∈ AD, причем AK/KD = 1/2, Р — середина АВ. Выразите вектор через векторы BP и BC

Видео:1. Векторы и параллелограмм задачи №1Скачать

Ваш ответ

Видео:№933. Найдите координаты вершины D параллелограмма ABCD, если А (0; 0), B (5; 0), С (12; -3.).Скачать

решение вопроса

Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Похожие вопросы

• Все категории
• экономические 43,282
• гуманитарные 33,619
• юридические 17,900
• школьный раздел 606,989
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

На стороне ad параллелограмма abcd отложен вектор ak длины ak 1 5 ad

Сторона AB параллелограмма ABCD вдвое больше стороны AD. Точка K — середина стороны AB. Докажите, что DK — биссектриса угла ADC.

Проведём FK параллельно AD (см. рис.). Имеем AD = AK = KB, следовательно, параллелограмм AKFD является ромбом. Диагональ DK ромба AKFD является биссектрисой угла ADC.

🔥 Видео

Точка E середина стороны AD параллелограмма ABCDСкачать

Площадь параллелограмма, построенного на данных векторахСкачать

Найдите вершину A параллелограмма ABCD, если B(3; −4; 7), C(−5; 3; −2) и D(1; 2; −3)Скачать

Нахождение длины вектора через координаты. Практическая часть. 9 класс.Скачать

№784. В паралеллограмме ABCD диагонали пересекаются в точке О, а М— точка на стороне AD, такая,Скачать

Выразить векторы. Разложить векторы. Задачи по рисункам. ГеометрияСкачать

егэ векторы решу егэ все задания №2 профильСкачать

№358. Дан параллелепипед ABCDA1B1C1D1. Назовите вектор, начало и конец которого являются вершинамиСкачать

№748. Диагонали параллелограмма ABCD пересекаются в точке O. Равны ли векторы?Скачать

Скалярное произведение векторов. 9 класс.Скачать

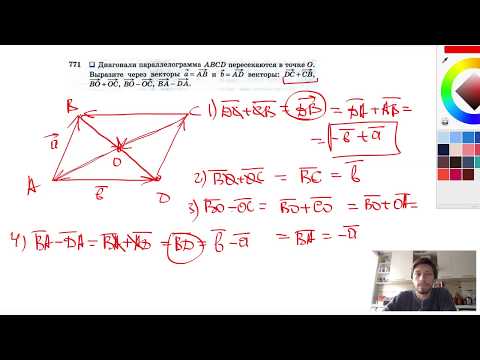
№771. В параллелограмме ABCD диагонали пересекаются в точке ОСкачать

Математика без Ху!ни. Угол между векторами, применение скалярного произведения.Скачать

Математика без Ху!ни. Смешанное произведение векторовСкачать