Создать вектор c вторым способом количество элементов которого равно 6 маткад (4 видео)

Создать вектор c вторым способом количество элементов которого равно 6 маткад

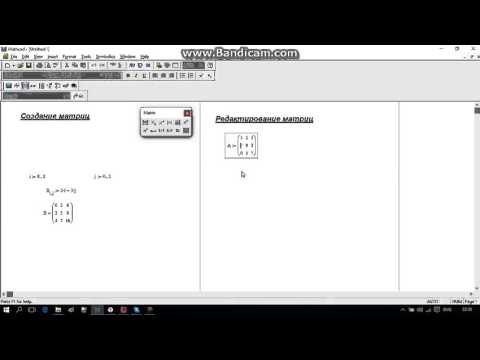
Одиночное число в Mathcad называется скаляром. Столбец чисел называется вектором, а прямоугольная таблица чисел — матрицей. Общий термин для вектора или матрицы — массив.

Имеются три способа создать массив:

Заполняя массив пустых полей, как обсуждается в этом разделе. Эта методика подходит для не слишком больших массивов.
Используя дискретный аргумент, чтобы определить элементы с его помощью, как обсуждено в следующей главе. Эта методика подходит, когда имеется некоторая явная формула для вычисления элементов через их индексы.
Считывая их из файлов данных.

Можно различать имена матриц, векторов и скаляров, используя различный шрифт для их написания. Например, во многих математических и инженерных книгах имена векторов пишутся жирным, а имена скалярных переменных — курсивом.

Вектор — массив или матрица, содержащая один столбец. Чтобы создать вектор в Mathcad, выполните следующее:

Щёлкните в свободном месте или на поле.

Выберите Матрицы из меню Математика или нажмите [Ctrl]M. Появляетс я диалоговое окно, как на рисунке справа.

Укажите число строк, равное числу элементов вектора, в поле “Строк”. Например, чтобы создать вектор с тремя элементами, напечатайте 3.
Напечатайте 1 в поле “Столбцов”, затем нажмите “Создать”. Mathcad создает вектор с пустыми полями для заполнения.

На следующем этапе нужно заполнить эти поля скалярными выражениями. Для этого выполните следующее:

Щёлкните на верхнем поле и напечатайте 2.

Переместите выделяющую рамку в следующее поле. Можно сделать это или клавишей [Tab], или щёлкнув непосредственно на втором поле.

Напечатайте 3 во втором поле. Затем переместите выделяющую рамку в третье поле, и напечатайте 4.

Если понадобится создавать еще векторы, можно оставить диалоговое окно “Матрицы” открытым для дальнейшего использования.

Как только вектор создан, можно использовать его в вычислениях в точности так же, как и число. Например, чтобы добавить другой вектор к этому вектору, необходимо выполнить следующее:

Нажмите [ ] несколько раз или щёлкните на любой из скобок вектора. Выделяющая рамка теперь заключает весь вектор. Это означает, что знак плюс, который будет напечатан, относится к вектору целиком, а не к какому-либо из элементов.

Нажмите клавишу плюс (+). Mathcad показывает поле для второго вектора.

Используйте диалоговое окно “Матрицы”, чтобы создать другой вектор с тремя элементами.

Заполните этот вектор, щелкая в каждом поле и печатая числа, показанные справа. Можно также использовать [Tab], чтобы двигаться от одного элемента к другому.

Нажмите знак =, чтобы увидеть результат.

Сложение — только одна из операций Mathcad, определенных для векторов и матриц. В Mathcad также есть вычитание матриц, умножение матриц, скалярное произведение, целочисленные степени, детерминанты и много других операторов и функций для векторов и матриц. Полные списки появляются в разделах “Векторные и матричные операторы” и “Векторные и матричные функции” ниже в этой главе.

Если Вы используете Mathcad PLUS, Вы сможете выполнить много символьных операций с матрицами. Подробнее об этом см.в Главе “Символьные вычисления”.

Чтобы создать матрицу, сначала щёлкните в свободном месте или на поле. Затем:

Выберите Матрицы из меню Математика, или нажмите [Ctrl]M. Появится диалоговое окно.

Введите число строк и столбцов в нужные поля. В этом примере матрица имеет две строки и три столбца. Затем нажмите на “Создать”. Mathcad создаст матрицу с пустыми полями.

В завершение заполните поля, как описано в предыдущем разделе для векторов.

Можно использовать эту матрицу в формулах в точности так же, как и число или вектор.

Везде в настоящем руководстве термин вектор относится к вектору-столбцу. Вектор-столбец идентичен матрице с одним столбцом. Можно также создать вектор-строку, создав матрицу с одной строкой и многими столбцами. Операторы и функции, которые берут векторный аргумент, всегда ожидают вектор-столбец. Они не применимы к векторам-строкам. Чтобы превратить вектор-строку в вектор-столбец, используйте оператор транспонирования[Ctrl]1.

Изменение размера матрицы

Можно изменять размер матрицы, вставляя и удаляя строки и столбцы. Для этого необходимо выполнить следующее:

Щёлкните на одном из элементов матрицы, чтобы заключить его в выделяющую рамку. Mathcad будет начинать вставку или удаление с этого элемента.

Выберите Матрицы из меню Математика. Появляется диалоговое окно.

Напечатайте число строк и-или столбцов, которые нужно вставить или удалить. Затем нажмите на “Вставить” или на “Удалить”. Например, чтобы удалить столбец, который содержит выбранный элемент, напечайте 1 в поле “Столбцов”, 0 в поле “Строк”, и нажмите на “Удалить”.

Вот как Mathcad будет удалять или вставлять строки или столбцы, в зависимости от того, что впечатывается в диалоговое окно:

Если вставляются строки, Mathcad создает строки пустых полей ниже выбранного элемента. Если вставляются столбцы, Mathcad создает столбцы пустых полей справа от выбранного элемента.
Чтобы вставить строку выше верхней строки или столбец слева от первого столбца, сначала заключите матрицу целиком в выделяющую рамку, щёлкнув внутри и нажав [ ] несколько раз. Затем выберите Матрицы и продолжите, как обычно.
Когда строки или столбцы удаляются, Mathcad начинает со строки или столбца, занятых выбранным элементом. Mathcad удаляет строки вниз от этого элемента и столбцы — направо от этого элемента.
Если напечатать 0 в поле “Строк”, Mathcad ни вставит, ни удалит строки. Если напечатать 0 в поле “Столбцов”, Mathcad ни вставит, ни удалит столбцы.

Обратите внимание, что при удалении строк или столбцов Mathcad выбрасывает содержащуюся в них информацию.

Чтобы удалить всю матрицу или вектор, заключите их в выделяющую рамку и выберите Вырезать из меню Правка.

Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter

Содержание

Задания к лабораторной работе 3
Векторы и матрицы в MathСad
Работа с матрицами
Добавление и вычитание
📽️ Видео

Видео:МАТКАД МатрицыСкачать

Задания к лабораторной работе 3

Лабораторная работа 2.

Тема: Векторы и матрицы

Цель: научить создавать векторы и матрицы разными способами, производить с ними различные операции.

Общие сведения

Задачи линейной алгебры, решаемые в MathCAD, можно условно разделить на два класса. Первый ‑ это простейшие матричные операции, которые сводятся к определенным арифметическим действиям над элементами матрицы. Они реализованы в виде операторов и нескольких специфических функций, предназначенных для создания, объединения, сортировки, получения основных свойств матриц и т. д. Второй класс ‑ это более сложные действия, которые реализуют алгоритмы вычислительной линейной алгебры, такие как вычисление определителей и обращение матриц, вычисление собственных векторов и собственных значений, решение систем линейных алгебраических уравнений и различные матричные разложения.

Простейшие операции матричной алгебры реализованы в MathCAD в виде операторов, причем их запись максимально приближена к математическому значению. Каждый оператор выражается соответствующим символом. Некоторые операции применимы только к квадратным матрицам N ´ N, некоторые допускаются только для векторов (например, скалярное произведение), а другие, несмотря на одинаковое написание, по-разному действуют на векторы и матрицы.

Имеется два способа создать матрицу.

1-й способ. Использование команды создания массивов:

· Воспользоваться командой Вставка ® Матрица;

· нажатие клавиш Ctrl+M;

· выбор пиктограммы с изображением шаблона матрицы на панели инструментов Матрицы.

В диалоговом окне указать размерность матрицы, т. е. количество ее строк m (Rows) и столбцов n (Columns).

Для векторов один из этих параметров должен быть равен 1. При m = 1 получим вектор-столбец, а при n = 1- вектор-строку.

Далее на экране появится шаблон , в который нужно ввести значения элементов массива.

Обращаться к отдельным элементам вектора или матрицы можно используя нижний индекс. Для элемента матрицы указываются два индекса, один ‑ для номера строки, другой ‑ для номера столбца.

Чтобы ввести нижний индекс, нужно нажать клавишу [ после имени вектора или матрицы или выбрать команду на панели Матрицы.

2-й способ. Использование ранжированной переменной.

Ранжированная переменная используется для определения индекса (номера) элемента массива.

1) Создать матрицу В, состоящую из 2 строк и 3 столбцов.

2) Создать вектор S, состоящий из 3 элементов

Команды панели инструментов Матрицы

Кнопка	Назначение
	Создание матрицы
	Обратная матрица
	Определитель матрицы
	Транспонирование матрицы
	Выделение столбца матрицы

Операторы для работы с массивами

Обозначения: для векторов ‑ V, для матриц ‑ М и для скалярных величин ‑ z.

Оператор	Ввод	Назначение оператора
V1+V2	V1+V2	Сложение двух векторов V1 и V2
V1-V2	V1-V2	Вычитание двух векторовV1 и V2
-М	-М	Смена знака у элементов матрицы M
V-z	V-z	Вычитание из вектора V скаляра z
zV, Vz	zV, Vz	Умножение вектора V на скаляр z
zM, Mz	zM, Mz	Умножение матрицы М на скаляр z
V1*V2	VI*V2	Умножение двух векторов V1 и V2
M*V	M*V	Умножение матрицы М на вектор V
М1*М2	М1*М2	Умножение двух матриц М1 и М2
	V/z	Деление вектора V на скаляр z
	M/z	Деление матрицы М на скаляр z
	М^n	Возведение матрицы М в степень п

Фрагмент документа MathCAD:

Функции для работы с векторами и матрицами.

Некоторые из них (V должен быть вектором, A может быть вектором либо матрицей):

length(V) ‑возвращает число элементов в векторе v;

last(V) ‑ возвращает индекс последнего элемента;

max(A) ‑ возвращает максимальный по значению элемент;

min(A) ‑ возвращает минимальный по значению элемент.

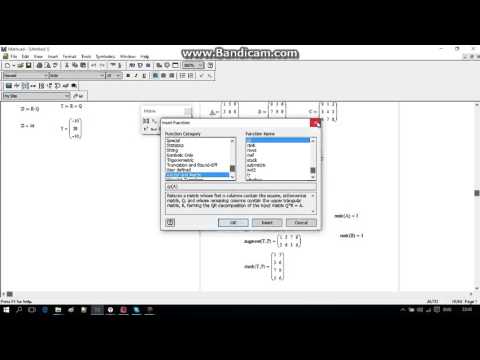
Для работы с матрицами также существует ряд встроенных функций:

augment(M1, М2) ‑ объединяет в одну матрицы М1 и М2, имеющие одинаковое число строк;

identity(n) ‑ создает единичную квадратную матрицу размером , (n – размер матрицы(число));

stack(MI, M2) ‑ объединяет две матрицы М1 и M2, имеющие одинаковое число столбцов, сажая M1 над M2;

diag(V) ‑ создает диагональную матрицу, элемент главной диагонали которой ‑ вектор V;

cols(M) ‑ возвращает число столбцов матрицы М;

rows(M) ‑ возвращает число строк матрицы М;

rank(M) ‑возвращает ранг матрицы М;

tr(M) ‑ возвращает след (сумму диагональных элементов) квадратной матрицы М;

mean(M) ‑ возвращает среднее значение элементов массива М;

median(M) ‑ возвращает медиану элементов массива М;

eigenvals(M) ‑ возвращает вектор, элементами которого являются собственные значения матрицы M (M должна быть квадратной матрицей.);

submatrix(M,ir,jr,ic,jc) ‑ возвращает подмассив, состоящий из всех элементов, которые содержатся в строках с ir по jr и столбцах с ic по jc массива М.

Все матричные и векторные операторы допустимо использовать как в численных, так и в символьных расчетах. Мощь символьных операций заключается в возможности проводить их не только над конкретными числами, но и над переменными.

Фрагмент документа MathCAD:

Задания к лабораторной работе 3

1. Ввести в документ название лабораторной работы, вариант задания и фамилию студента

2. Создать квадратные матрицы А, В, D, размером (5,5,4 соответственно) первым способом

3. Исследовать следующие свойства матриц на примере преобразования заданных массивов:

· транспонированная матрица суммы двух матриц равна сумме транспонированных матриц (A+B) T =A T +B T ;

· транспонированная матрица произведения двух матриц равна сумме произведению транспонированных матриц, взятых в обратном порядке: (A*B) T =B T *A T ;

· при транспонировании квадратной матрицы определитель не меняется : |D|=|D T |;

· произведение квадратной матрицы на соответствующую ей квадратную дает единичную матрицу (элементы главной диагонали единичной матрицы равны 1, а все остальные – 0) D*D -1 =E.

4. Для матриц A,B найти обратные матрицы.

5. Найти определители матриц A,B.

6. Для матрицы А увеличить значения элементов в № раз, где № ‑ номер варианта.

7. Для матрицы В увеличить значения элементов на №.

8. Создать вектор C вторым способом, количество элементов которого равно 6.

9. Применить к матрицам А, В, D встроенные матричные функции (всевозможные) из приведенных в пункте “Функции для работы…..”

10. Применить к вектору С встроенные векторные функции.

11. Применить ко всем матрицам и вектору общие встроенные функции.

12. Сохранить документ.

1. Как создать матрицу, вектор ‑ строку, вектор ‑ столбец?

2. Какие операторы есть для работы с матрицами?

3. Перечислите команды панели инструментов Матрицы.

4. Как вставить матричные функции?

5. Как выполнять вычисления, если матрица задана в символьном виде?

Видео:Основные действия с матрицами и векторами в MathCAD 14 (20/34)Скачать

Векторы и матрицы в MathСad

Вы уже наверняка не раз сталкивались с такими понятиями как векторы и матрицы. Вектор – это обыкновенный столбец с числами. Матрица представляет собой сборный блок с объектами. Именно на работе с этими элементами построен принцип функционирования программы Excel. В этом уроке мы расскажем о том, как работать с такими вычислениями в программе Маткад и акцентируем внимание на том, почему процесс работы в данном ПО куда проще и удобнее.

Мы уже рассказывали в своих уроках о том, что все наши векторы начинались с элемента с нулевым значением. Сейчас же мы поставим номером первого элемента цифру один, ведь так нам гораздо проще будет сориентироваться в учебном материале.

Данное значение можно внести прямо в рабочее поле.

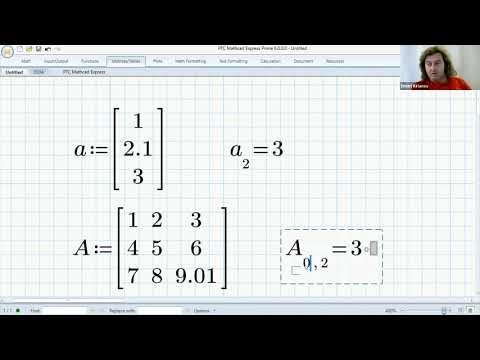
Посмотрите на матрицы на рисунке ниже.

Как вы можете заметить, в них входят и числа, и функции. Помимо этого, сюда можно внести и текст. Чтобы вывести элемент матрицы, воспользуйтесь подстрочным индексом.

Матрицы, описанные на скрине повыше, относятся к квадратному типу. Тем не менее, пользователь может самостоятельно устанавливать их размерные рамки.

Примите во внимание, что первое число обозначает общую нумерацию строчки, а второе – номер столбика.

Для векторного столбца второй индекс можно удалить. Для строки же он является обязательным.

Нужные команды, для всевозможного выделения строчек или столбиков вы всегда сможете отыскать во вкладке «Математика».

Большинство операций для векторных и матричных конструкций вполне соответствуют работе со стандартными числами и функциями. Для того, чтобы отыскать обратную матрицу, потребуется действовать по аналогии с операциями деления. Пользователь может записать операторы, задав им наименования матриц и векторов. Например, это может выглядеть так:

Более подробно мы рассмотрим данный опционал немного погодя. Стоит отметить, что такая функция нуждается в девяти операциях умножения и в таком же количестве деления. Согласитесь, что расписывать все эти процессы достаточно скучно. К тому же, с большими матрицами такой подход нерациональный.

Методика применения векторов отличается значительным разнообразием. Чтобы разработать вектор или матрицу, понадобится открыть вкладку «Вставить матрицу». На экране появится сетка с изображением маленьких квадратиков.

Перемещаем указатель на эту сетку. Настраиваем курсор на нужные габариты матрицы. Кликаем дважды ЛКМ.

На экране появляется новая матрица.

Матрица может быть переименована, после того, как пользователь дважды кликнет по левой скобке.

Чтобы быстро вставить или удалить строчки да столбцы, можно вызвать контекстное меню «Операторы с векторамиматрицами» на одноименной вкладке.

Работа с матрицами

Эффекты от матриц или вектором гораздо проще сообразить, пользуясь специально разработанными символами. Обратите внимание на скрин ниже.

Оператор транспортировки вызывается посредством выполнения операции Математика –> Операторы –> Векторы и матрицы:

Кликаем по правой стороне матрицы и применяем оператор. Он подходит как для символьных, так и численных матриц.

Операции в векторах часто выполняются по одному элементу. В этой ситуации можно воспользоваться очень удобным оператором, который отвечает за разработку вектора. Чтобы перемножить два вектора, понадобится выполнить простой пример.

Теперь нам нужно выбрать нужные параметры и активировать векторизацию.

Вычисляем заданные параметры и смотрим на результат. Первый элемент приумножился на второй, и так далее.

Еще примеры таких опций.

Операции поэлементного типа могут применяться исключительно к массивам одинакового размера.

Добавление и вычитание

Данные операции относятся к поэлементному типу.

Она также применяется к массивам одинакового размерного типа.

Пользуясь оператором, предназначенным для суммирования, можно отыскать сумму всех векторных частей.

Скалярное произведение работает по представленному ниже принципу.

При таком типе умножения матриц, программа занимается умножением данных элементов по столбцам. Данная операция может применяться исключительно к тем матрицам, которые характеризуются равным количеством строчек и столбцов.

Обратите внимание, что немалая роль отводится поочередности множителей.

Только в редких случаях скалярное произведение может стать коммутативным.

Скаляр двух векторов показывает результат как на фотографии ниже.

Данная опция может использоваться исключительно для двух векторных столбов из трех элементов.

Векторное произведение часто используется для механики, гидродинамики и огромного количества подобных сфер деятельности.

Обратная матрица может быть применима для квадратных матриц:

В результате у нас получится матрица единичного типа

Если произвести матрицу и единичную матрицу, мы получим первоначальный вариант.

Определитель может быть разработан исключительно для матрицы квадратного типа. Он может быть нулевым в любых условиях. Обратная матрица имеет в своей структуре дроби, в состав которых входит определитель.

В ситуациях, когда определитель установлен на ноль, к нему нереально подобрать обратную матрицу. Сама матрица автоматически становится сингулярной. О таких изменениях пользователь узнает из оповещения программы.

В ситуациях со скалярами, определитель соответствует их модулям

Команда «определитель» помогает отыскать длину вектора .

Уважаемые пользователи, хотим Вас проинформировать о том, что некоторые антивирусные программы и браузеры ложно срабатывают на дистрибутив программы MediaGet, считая его зараженным. Данный софт не содержит никаких вредоносных программ и вирусов и многие из антивирусов просто Вас предупреждают, что это загрузчик (Downloader). Если хотите избежать подобных проблем, просто добавьте MediaGet в список доверенных программ Вашей антивирусной программы или браузера.

Выбрав нужную версию программы и кликнув ссылку, Вам на компьютер скачивается дистрибутив приложения MediaGet, который будет находиться в папке «Загрузки» для Вашего браузера. Находим этот файл с именем программы и запускаем его. И видим первый этап установки. Нажимаем унопку «Далее»

Далее Вам предлагается прочитать и одобрить лицензионное соглашение. Нажимаем кнопку «Принимаю»

В следующем окне Вам предлагается бесплатное полезное дополнительное программоное обеспечение, будь то антивирус или бразуер. Нажимаем кнопку «Принимаю». Также Вы можете отказаться от установки дополнительного ПО, нажав кнопку «Отклоняю»

Далее происходит процесс установки программы. Вам нужно выбрать папку, в которую будут скачиваться нужные Вам файлы.

Происходит завершение установки. Программа автоматически открывается и скачивает нужные Вам исходные файлы.

Обратите внимание, что предоставляемое программное обеспечение выкладывается исключительно для личного использования и ознакомления. Все файлы, доступные для скачивания, не содержат вирусов и вредоносных программ.