Соотношение площадей треугольников образованных диагоналями выпуклого четырехугольника

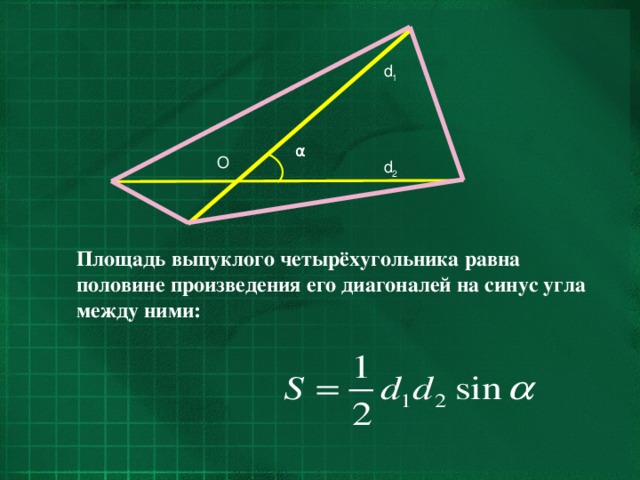
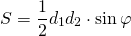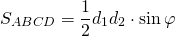Площадь выпуклого четырехугольника равна половине произведения его диагоналей на синус угла между ними:

(d₁, d₂ — диагонали четырёхугольника, φ — угол между ними).

Дано: ABCD — выпуклый четырёхугольник,

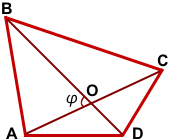
Диагонали выпуклого четырёхугольника ABCD делят его на 4 треугольника.

Видео:8 класс, 21 урок, Отношение площадей подобных треугольниковСкачать

VIII класс: Тема 3. Площади фигур. Теорема Пифагора

VIII класс: Тема 3. Площади фигур. Теорема Пифагора.

1. Понятие площади. Равновеликие фигуры.

Если длина – это числовая характеристика линии, то площадь – это числовая характеристика замкнутой фигуры. Несмотря на то, что с понятием площади мы хорошо знакомы из повседневной жизни, строгое определение этому понятию дать непросто. Оказывается, что площадью замкнутой фигуры можно назвать любую неотрицательную величину, обладающую следующими свойствами измерения площадей фигур:

Равные фигуры имеют равные площади. Если данную замкнутую фигуру разбить на несколько замкнутых фигур, то площадь фигуры равна сумме площадей составляющих ее фигур (фигура на рисунке 1 разбита на n фигур; в этом случае площадь фигуры , где Si – площадь i-ой фигуры).

В принципе, можно было бы придумать множество величин, обладающих сформулированными свойствами, а значит, характеризующих площадь фигуры. Но наиболее привычной и удобной является величина, характеризующая площадь квадрата как квадрат его стороны. Назовем эту «договоренность» третьим свойством измерения площадей фигур:

Площадь квадрата равна квадрату его стороны (рисунок 2).

При таком определении площадь фигур измеряют в квадратных единицах (см2, км2, га=100м2).

Фигуры, имеющие равные площади, называются равновеликими.

Замечание: Равные фигуры имеют равные площади, то есть равные фигуры равновелики. Но равновеликие фигуры далеко не всегда равны (например, на рисунке 3 изображены квадрат и равнобедренный треугольник, составленные из равных прямоугольных треугольников (кстати, такие фигуры называют равносоставленными); понятно, что квадрат и треугольник равновелики, но не равны, поскольку не совмещаются наложением).

Далее выведем формулы для вычисления площадей всех основных видов многоугольников (в том числе всем известную формулу для нахождения площади прямоугольника), опираясь на сформулированные свойства измерения площадей фигур.

2. Площадь прямоугольника. Площадь параллелограмма.

Формула для вычисления площади прямоугольника: Площадь прямоугольника равна произведению двух его смежных сторон (рисунок 4).

AD=a, AB=b.

1. Удлиним сторону AB на отрезок BP=a, а сторону AD – на отрезок DV=b. Построим параллелограмм APRV (рисунок 4). Поскольку ÐA=90°, APRV – прямоугольник. При этом AP=a+b=AV, Þ APRV – квадрат со стороной (a+b).

2. Обозначим BCÇRV=T, CDÇPR=Q. Тогда BCQP – квадрат со стороной a, CDVT – квадрат со стороной b, CQRT – прямоугольник со сторонами a и b.

3. . #

Формула для вычисления площади параллелограмма: Площадь параллелограмма равна произведению его высоты на основание (рисунок 5).

Замечание: Основанием параллелограмма принято называть ту сторону, к которой проведена высота; понятно, что основанием может служить любая сторона параллелограмма.

BH^AD, HÎAD.

Доказательство:

1. Проведем к основанию AD высоту CF (рисунок 5).

2. BCïêHF, BHïêCF, Þ BCFH — п/г по определению. ÐH=90°, ÞBCFH – прямоугольник.

3. BCFH – п/г, Þ по свойству п/г BH=CF, Þ DBAH=DCDF по гипотенузе и катету (AB=CD по св-ву п/г, BH=CF).

3. Площадь треугольника.

Формула для вычисления площади треугольника: Площадь треугольника равна половине произведения его высоты на основание (рисунок 6).

Замечание: Основанием треугольника в данном случае называют сторону, к которой проведена высота. Любая из трех сторон треугольника может служить его основанием.

Дано:

BD^AC, DÎAC.

Доказать: .

1. Достроим DABC до п/г ABKC путем проведения через вершину B прямой BKïêAC, а через вершину C – прямой CKïêAB (рисунок 6).

2. DABC=DKCB по трем сторонам (BC – общая, AB=KC и AC=KB по св-ву п/г), Þ . #

Следствие 1 (формула для вычисления площади прямоугольного треугольника): Поскольку в п/у D‑ке один из катетов является высотой, проведенной ко второму катету, площадь п/у D-ка равна половине произведения его катетов (на рисунке 7 ).

Следствие 2: Если рассмотреть п/у DABC с высотой AH, проведенной к гипотенузе BC, то . Таким образом, в п/у D-ке высота, проведенная к гипотенузе, равна отношению произведения его катетов к гипотенузе. Это соотношение достаточно часто используется при решении задач.

4. Следствия из формулы для нахождения площади треугольника: отношение площадей треугольников с равными высотами или основаниями; равновеликие треугольники в фигурах; свойство площадей треугольников, образованных диагоналями выпуклого четырехугольника.

Из формулы для вычисления площади треугольника элементарным образом вытекают два следствия:

1. Отношение площадей треугольников с равными высотами равно отношению их оснований (на рисунке 8 ).

2. Отношение площадей треугольников с равными основаниями равно отношению их высот (на рисунке 9 ).

Замечание: При решении задач очень часто встречаются треугольники с общей высотой. При этом, как правило, их основания лежат на одной прямой, а вершина, противолежащая основаниям – общая (к примеру, на рисунке 10 S1:S2:S3=a:b:c). Следует научиться видеть общую высоту таких треугольников.

Также из формулы для вычисления площади треугольника вытекают полезные факты, позволяющие находить равновеликие треугольники в фигурах:

1. Медиана произвольного треугольника разбивает его на два равновеликих треугольника (на рисунке 11 у DABM и DACM высота AH – общая, а основания BM и CM равны по определению медианы; отсюда следует, что DABM и DACM равновелики).

2. Диагонали параллелограмма разбивают его на четыре равновеликих треугольника (на рисунке 12 AO – медиана треугольника ABD по свойству диагоналей п/г, Þ в силу предыдущего св-ва треугольники ABO и ADO равновелики; т. к. BO – медиана треугольника ABC, треугольники ABO и BCO равновелики; т. к. CO – медиана треугольника BCD, треугольники BCO и DCO равновелики; таким образом, SDADO=SDABO=SDBCO=SDDCO).

3. Диагонали трапеции разбивают ее на четыре треугольника; два из них, прилежащие к боковым сторонам, равновелики (рисунок 13).

BCïêAD; ACÇBD=O.

1. Проведем высоты BF и CH (рисунок 13). Тогда у DABD и DACD основание AD – общее, а высоты BF и CH равны; Þ SDABD=SDACD.

Если провести диагонали выпуклого четырехугольника (рисунок 14), образуется четыре треугольника, площади которых связаны очень простым для запоминания соотношением. Вывод этого соотношения опирается исключительно на формулу для вычисления площади треугольника; однако, в литературе оно встречается достаточно редко. Будучи полезным при решении задач, соотношение, которое будет сформулировано и доказано ниже, заслуживает пристального внимания:

Свойство площадей треугольников, образованных диагоналями выпуклого четырехугольника: Если диагонали выпуклого четырехугольника ABCD пересекаются в точке O, то (рисунок 14).

ABCD – выпуклый четырехугольник;

ACÇBD=O.

Доказать: .

3. . #

5. Отношение площадей треугольников, имеющих по равному углу.

Теорема об отношении площадей треугольников, имеющих по равному углу: Площади треугольников, имеющих по равному углу, относятся как произведения сторон, заключающих эти углы (рисунок 15).

Дано:

ÐBAC=ÐB1A1C1.

.

1. Отложим на луче AB отрезок AB2=A1B1, а на луче AC – отрезок AC2=A1C1 (рисунок 15). Тогда DAB2C2=DA1B1C1 по двум сторонам и углу между ними (AB2=A1B1 и AC2=A1C1 по построению, а ÐB2AC2=ÐB1A1C1 по условию). Значит, .

2. Соединим точки C и B2.

3. CH – общая высота DAB2C и DABC, Þ .

4. B2F — общая высота DAB2C и DAB2C2, Þ .

5. . #

6. Свойство биссектрисы треугольника.

С использованием теорем об отношении площадей треугольников, имеющих по равному углу, и об отношении площадей треугольников с равными высотами, просто доказывается исключительно полезный при решении задач факт, не имеющий непосредственного отношения к площадям фигур:

Свойство биссектрисы треугольника: Биссектриса треугольника делит сторону, к которой она проведена, на отрезки, пропорциональные прилежащим к ним сторонам.

Дано:

AK – биссектриса DABC.

Доказать: .

1. По теореме об отношении треугольников, имеющих по равному углу, .

2. Т. к. AH – общая высота треугольников ABK и ACK, .

3. Из пунктов 1 и 2 получаем: , Þ , Û . #

Замечание: Поскольку в верной пропорции можно менять местами крайние члены или средние члены, свойство биссектрисы треугольника удобнее запоминать в следующем виде (рисунок 16): .

7. Площадь трапеции.

Формула для вычисления площади трапеции: Площадь трапеции равна произведению ее высоты на полусумму оснований.

Дано:

Доказать: .

1. Проведем диагональ BD и высоту DF (рисунок 17). BHDF – прямоугольник, Þ BH = DF.

2.
.

Следствие: Отношение площадей трапеций с равными высотами равно отношению их средних линий (или отношению сумм оснований).

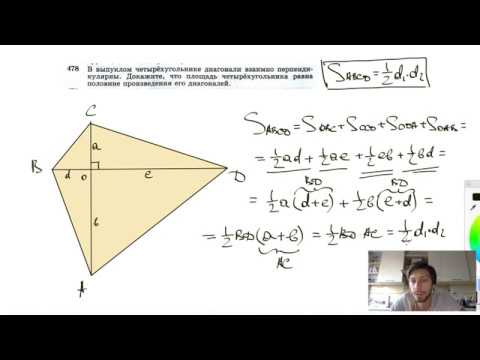
8. Площадь четырехугольника с взаимно перпендикулярными диагоналями.

Формула для вычисления площади четырехугольника с взаимно перпендикулярными диагоналями: Площадь четырехугольника с взаимно перпендикулярными диагоналями равна половине произведения его диагоналей.

Доказать: .

1. Обозначим ACÇBD=O. Поскольку AC^BD, AO – высота DABD, а CO – высота DCBD (рисунки 18а и 18б для случаев выпуклого и невыпуклого четырехугольников соответственно).

2.
(знаки «+» или «-» соответствуют случаям выпуклого и невыпуклого четырехугольников соответственно). #

9. Прямая и обратная теоремы Пифагора.

Теорема Пифагора играет исключительно важную роль в решении самых разнообразных задач; она позволяет находить неизвестную сторону прямоугольного треугольника по двум известным его сторонам. Известно множество доказательств теоремы Пифагора. Приведем наиболее простое из них, опирающееся на формулы для вычисления площадей квадрата и треугольника:

Теорема Пифагора: В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Дано:

ÐA=90°.

1. Обозначим AC=a, AB=b. Отложим на луче AB отрезок BP=a, а на луче AC – отрезок CV=b (рисунок 19). Проведем через точку P прямую PRïêAV, а через точку V – прямую VRïêAP. Тогда APRV — п/г по определению. При этом поскольку ÐA=90°, APRV – прямоугольник. А т. к. AV=a+b=AP, APRV – квадрат со стороной a+b, и SAPRV=(a+b)2. Далее поделим сторону PR точкой Q на отрезки PQ=b и QR=a, а сторону RV – точкой T на отрезки RT=b и TV=a.

2. DABC=DPQB=DRTQ=DVCT по двум катетам, Þ ÐACB=ÐPBQ=ÐRQT=ÐVTC, BC=QB=TQ=CT, и
.

4. . Итак, BC2=AB2+AC2. #

Обратная теорема Пифагора является признаком прямоугольного треугольника, т. е. позволяет по трем известным сторонам треугольника проверить, является ли он прямоугольным.

Обратная теорема Пифагора: Если квадрат стороны треугольника равен сумме квадратов двух других его сторон, то этот треугольник прямоугольный, а его большая сторона является гипотенузой.

BC2=AB2+AC2.

1. Построим прямой угол A1 и на его сторонах отложим отрезки A1B1=AB и A1C1=AC (рисунок 20). В полученном п/у DA1B1C1 по теореме Пифагора B1C12=A1B12+A1C12=AB2+AC2; но по условию AB2+AC2=BC2; Þ B1C12=BC2, Þ B1C1=BC.

Прямоугольные треугольники, длины сторон которых выражаются натуральными числами, называются пифагоровыми треугольниками, а тройки соответствующих натуральных чисел – пифагоровыми тройками. Пифагоровы тройки полезно помнить (большее из этих чисел равно сумме квадратов двух других). Приведем некоторые пифагоровы тройки:

Прямоугольный треугольник со сторонами 3, 4, 5 использовался в Египте для построения прямых углов, в связи с чем такой треугольник называют египетским.

10. Формула Герона.

Формула Герона позволяет находить площадь произвольного треугольника по трем его известным сторонам и является незаменимой при решении многих задач.

Формула Герона: Площадь треугольника со сторонами a, b и c вычисляется по следующей формуле: , где ‑ полупериметр треугольника.

BC=a; AC=b; AB=c.

Доказать: ,

где .

1. Пусть ÐB – наибольший из углов треугольника ABC (рисунок 21), тогда ÐA и ÐC – острые, и основание высоты BH лежит на стороне AC (а не на ее продолжении).

3. Из пункта 2 получаем: , Þ
. Подставим полученное выражение для x в формулу для вычисления высоты h и проведем преобразования:


(здесь учтено, что периметр DABC вдвое больше полупериметра: ). Тогда .

4. Подставим полученное выражение для высоты в формулу для вычисления площади треугольника: . #

Видео:ОГЭ Задание 24 Площадь выпуклого четырехугольника с перпендикулярными диагоналямиСкачать

Выпуклые четырехугольники.Специфика параллелограммов. Специфика трапеций.

Презентация разработана с целью подготовки мотивированных учащихся к решению задач повышенной сложности из модуля «Геометрия» ОГЭ по математике, содержит дополнительные сведения по теме «Четырехугольники».

Просмотр содержимого документа
«Выпуклые четырехугольники.Специфика параллелограммов. Специфика трапеций.»

ГОСУДАРСТВЕННАЯ ИТОГОВАЯ АТТЕСТАЦИЯ ОСНОВНОЙ ГОСУДАРСТВЕННЫЙ ЭКЗАМЕН МАТЕМАТИКА 9 КЛАСС МОДУЛЬ ГЕОМЕТРИЯ (часть 2) Выпуклые четырёхугольники Специфика параллелограммов Специфика трапеций

МБОУ СОШ №92 г. Кемерово

Денисова Татьяна Александровна

Площадь выпуклого четырёхугольника равна половине произведения его диагоналей на синус угла между ними:

Диагонали выпуклого четырёхугольника делят его на части так, что произведения площадей треугольников, прилегающих к противоположным сторонам четырёхугольника, равны:

Обоснование: найти площадь каждого из образованных диагоналями четырёх треугольников по формуле

Затем сложить эти площади (свойство 1) или перемножить ( свойство 2).

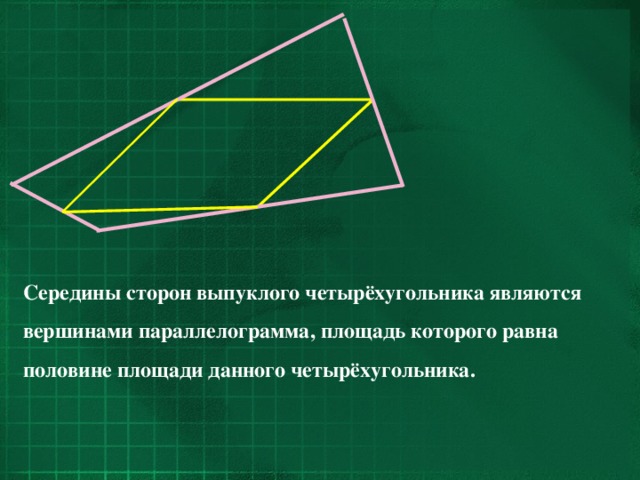
Середины сторон выпуклого четырёхугольника являются вершинами параллелограмма, площадь которого равна половине площади данного четырёхугольника.

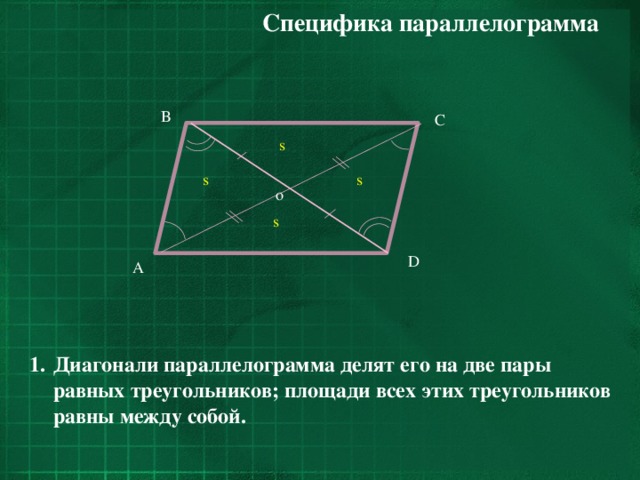
• Диагонали параллелограмма делят его на две пары равных треугольников; площади всех этих треугольников равны между собой.

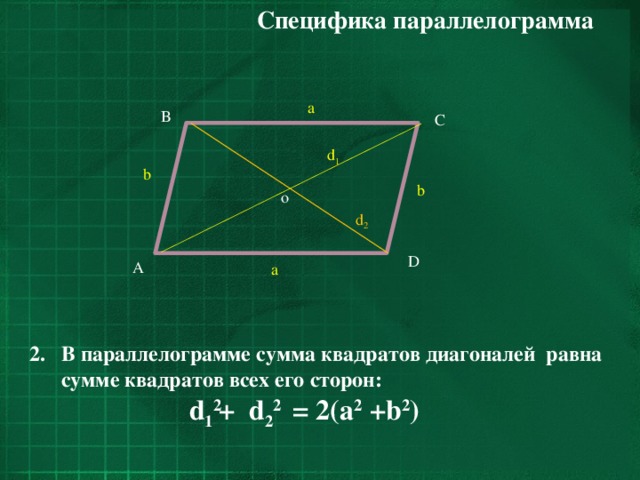
• В параллелограмме сумма квадратов диагоналей равна сумме квадратов всех его cторон:

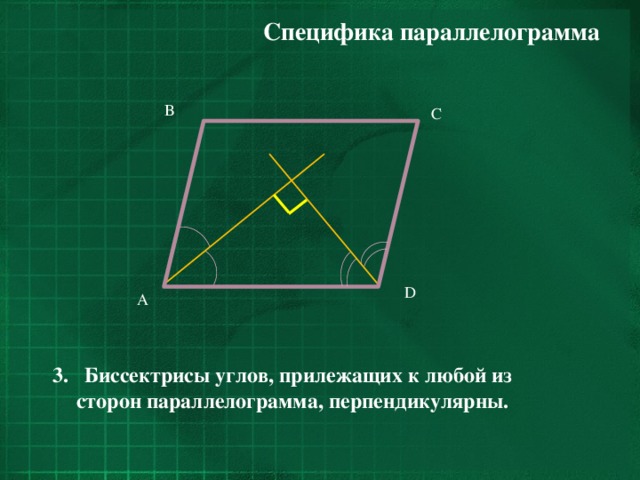
3. Биссектрисы углов, прилежащих к любой из сторон параллелограмма, перпендикулярны.

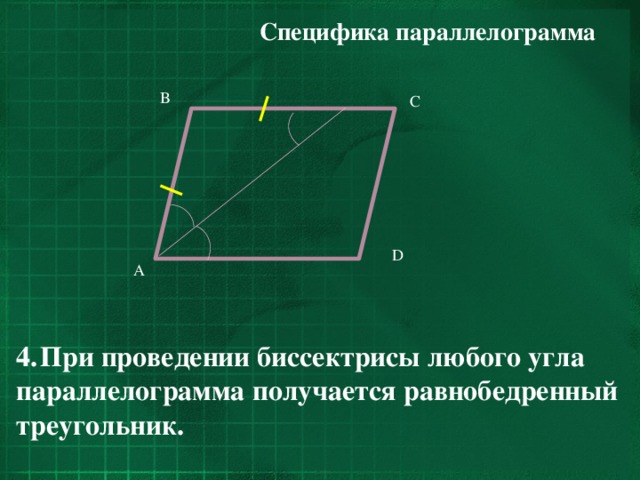
• При проведении биссектрисы любого угла

параллелограмма получается равнобедренный

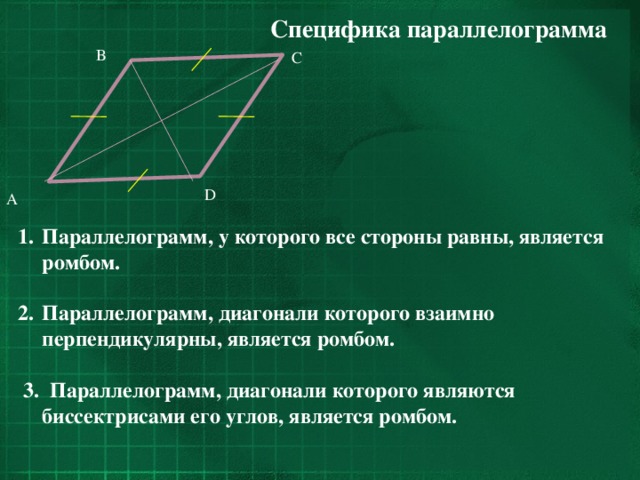
• Параллелограмм, у которого все стороны равны, является ромбом.

• Параллелограмм, диагонали которого взаимно перпендикулярны, является ромбом.

3. Параллелограмм, диагонали которого являются биссектрисами его углов, является ромбом.

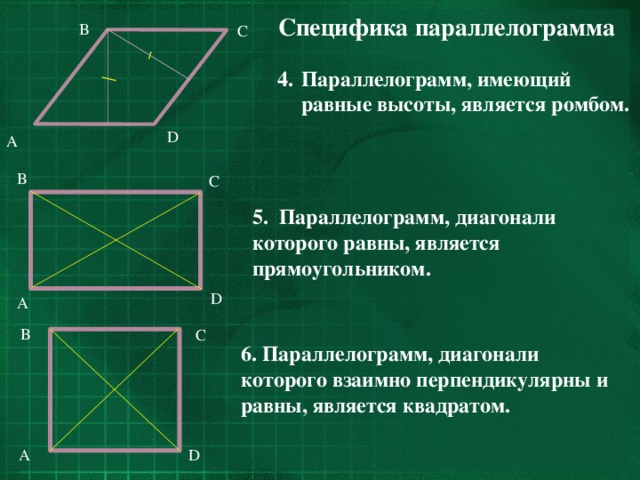
• Параллелограмм, имеющий равные высоты, является ромбом.

5. Параллелограмм, диагонали которого равны, является прямоугольником.

6. Параллелограмм, диагонали которого взаимно перпендикулярны и равны, является квадратом.

• Диагонали трапеции, пересекаясь, образуют

четыре треугольника, два из которых

равновелики, а два других – подобны с

коэффициентом подобия равным отношению

5. Диагонали трапеции делят её на четыре треугольника так, что произведение площадей тех из них, которые прилежат к основаниям, равно квадрату площади треугольника, прилежащего к любой из боковых сторон трапеции: S 1 S 2 = S 2 .

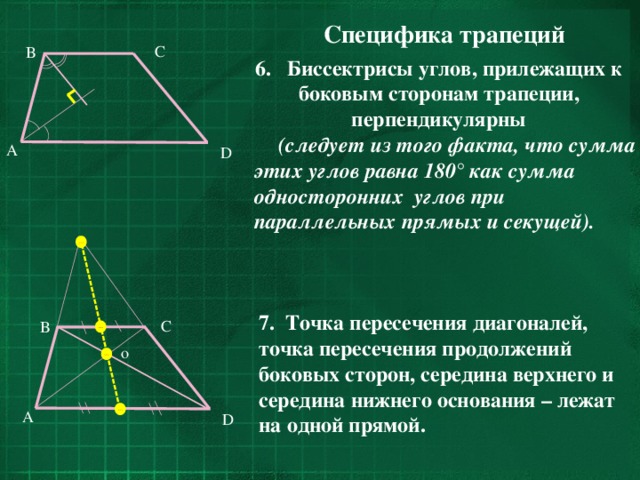
6. Биссектрисы углов, прилежащих к боковым сторонам трапеции, перпендикулярны

(следует из того факта, что сумма этих углов равна 180° как сумма односторонних углов при параллельных прямых и секущей).

7. Точка пересечения диагоналей, точка пересечения продолжений боковых сторон, середина верхнего и середина нижнего основания – лежат на одной прямой.

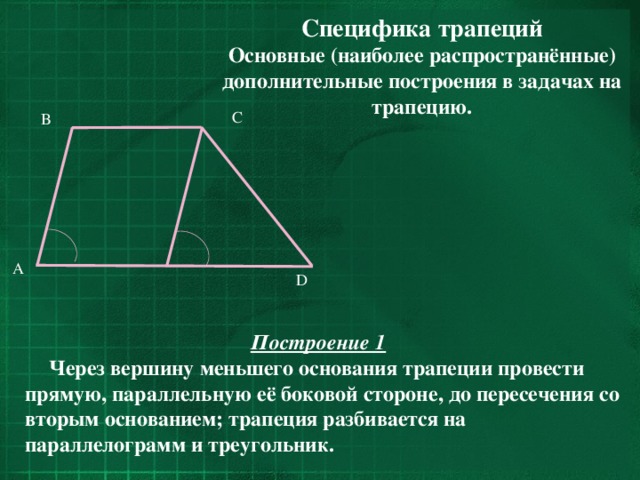
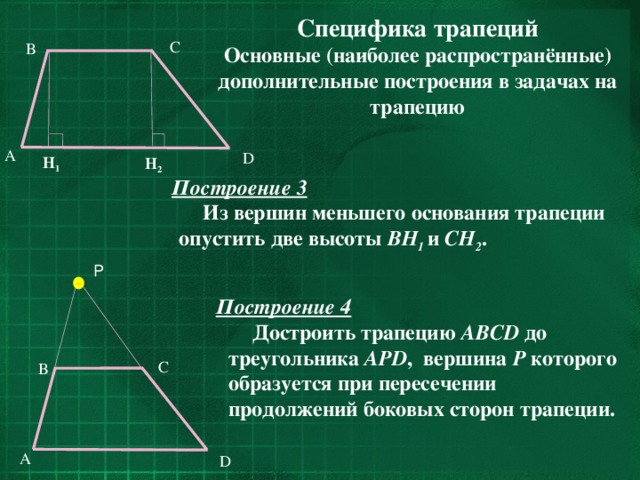
Основные (наиболее распространённые) дополнительные построения в задачах на трапецию.

Через вершину меньшего основания трапеции провести прямую, параллельную её боковой стороне, до пересечения со вторым основанием; трапеция разбивается на параллелограмм и треугольник.

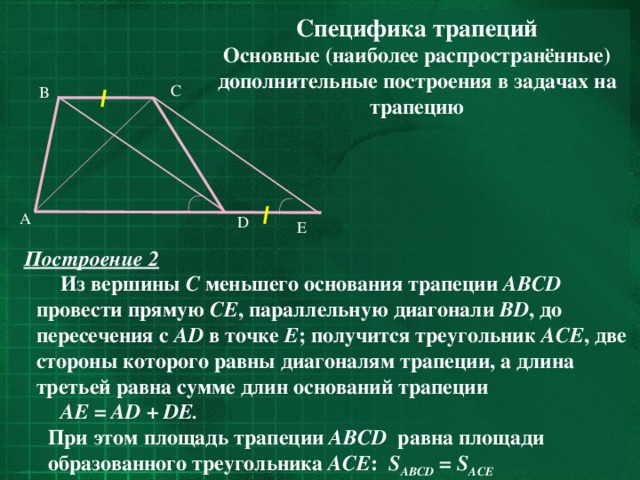
Основные (наиболее распространённые) дополнительные построения в задачах на трапецию

Из вершины С меньшего основания трапеции ABCD провести прямую CE , параллельную диагонали BD , до пересечения с AD в точке E ; получится треугольник ACE , две стороны которого равны диагоналям трапеции, а длина третьей равна сумме длин оснований трапеции

Основные (наиболее распространённые) дополнительные построения в задачах на трапецию

Достроить трапецию ABCD до треугольника APD , вершина Р которого образуется при пересечении продолжений боковых сторон трапеции.

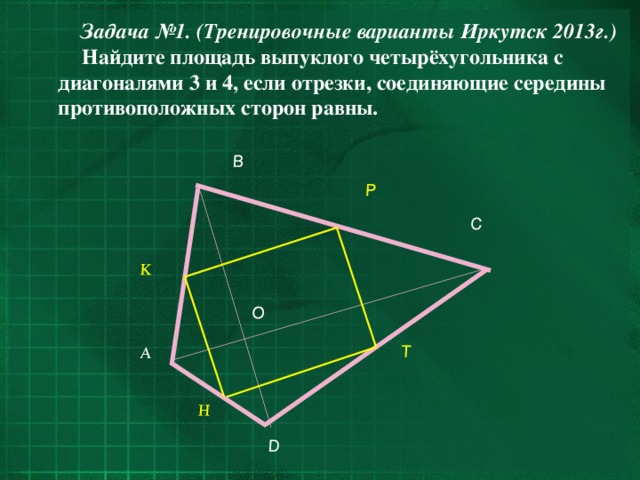
Задача №1. (Тренировочные варианты Иркутск 2013г.)

Найдите площадь выпуклого четырёхугольника с диагоналями 3 и 4, если отрезки, соединяющие середины противоположных сторон равны.

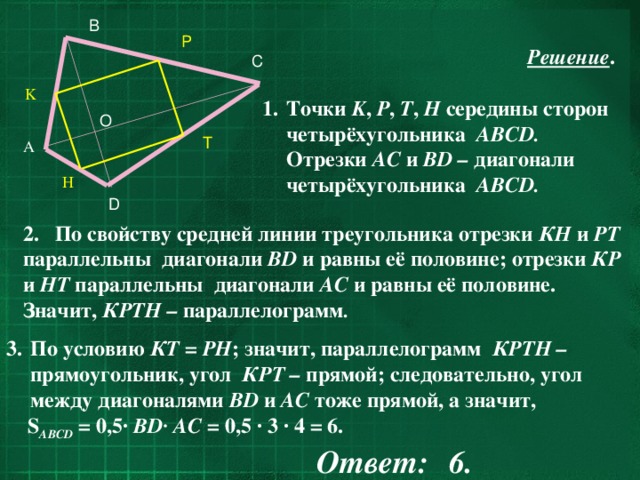
2. По свойству средней линии треугольника отрезки КН и РТ параллельны диагонали ВD и равны её половине; отрезки КР и НТ параллельны диагонали АС и равны её половине. Значит, КРТН – параллелограмм .

На стороне ВC параллелограмма ABCD выбрана точка К. Отрезки АК и ВD пересекаются в точке Р . Площадь параллелограмма ABCD равна 24, а площадь четырёхугольника РКСD равна 10. Найдите площадь треугольника АРD .

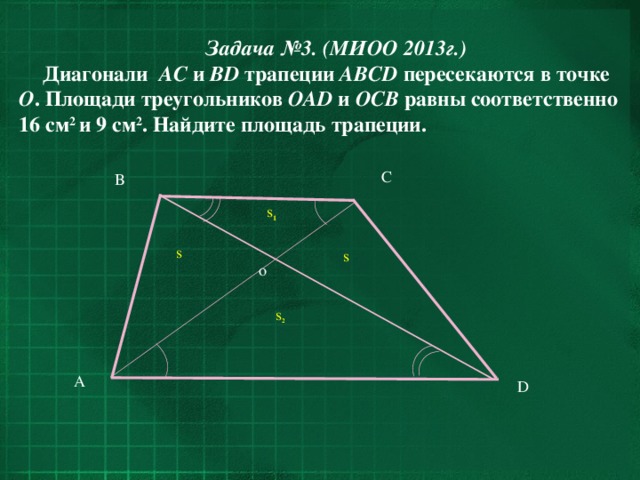
Диагонали AC и BD трапеции ABCD пересекаются в точке О . Площади треугольников OАD и OCВ равны соответственно 16 см 2 и 9 см 2 . Найдите площадь трапеции.

4. S BAD = S CAD , т. к. эти треугольники имеют общее основание AD и их высоты, проведённые к этому основанию, равны как высоты трапеции. Значит,

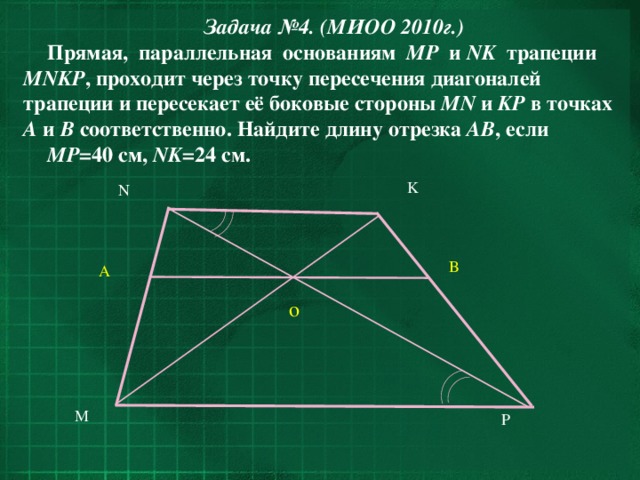
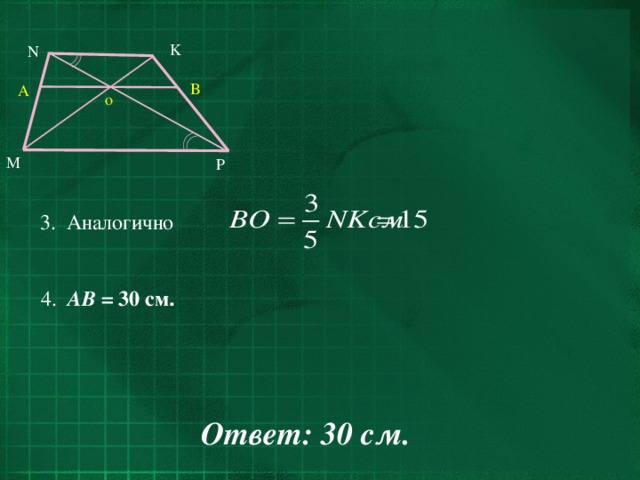
Прямая, параллельная основаниям MP и NK трапеции MNKP , проходит через точку пересечения диагоналей трапеции и пересекает её боковые стороны MN и KP в точках A и B соответственно. Найдите длину отрезка AB , если

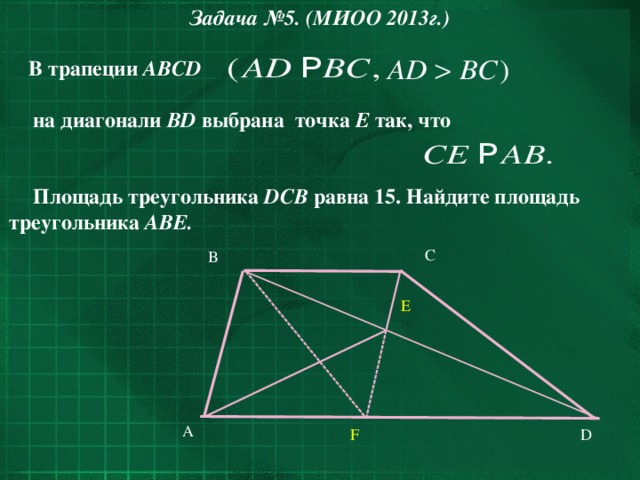
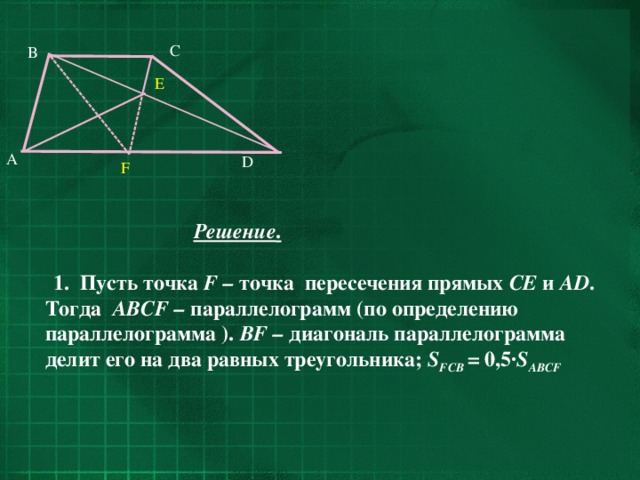
Площадь треугольника DCB равна 15. Найдите площадь треугольника АBЕ.

1. Пусть точка F – точка пересечения прямых CE и AD . Тогда ABCF – параллелограмм (по определению параллелограмма ). BF – диагональ параллелограмма делит его на два равных треугольника; S FCB = 0,5· S ABCF

2. S DCB = S FCB (как площади треугольников, имеющих общее основание и одинаковую высоту – высоту трапеции). Значит,

3.  AВE и параллелограмм ABCF имеют одно и то же основание AB и общую высоту, проведённую к AB. Значит,

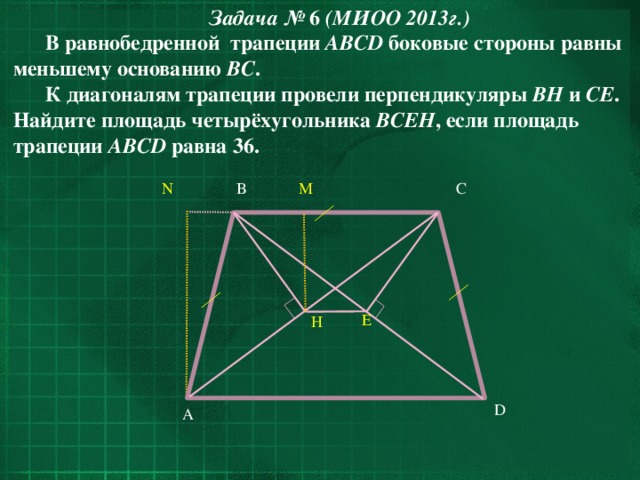
В равнобедренной трапеции ABCD боковые стороны равны меньшему основанию BC .

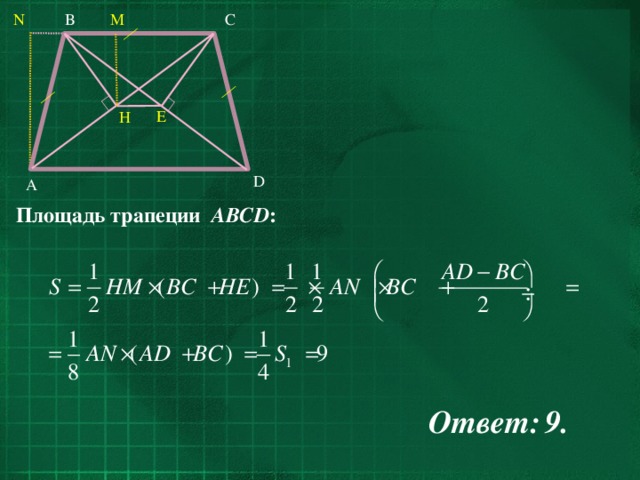
К диагоналям трапеции провели перпендикуляры BH и CE . Найдите площадь четырёхугольника BCEH , если площадь трапеции ABCD равна 36.

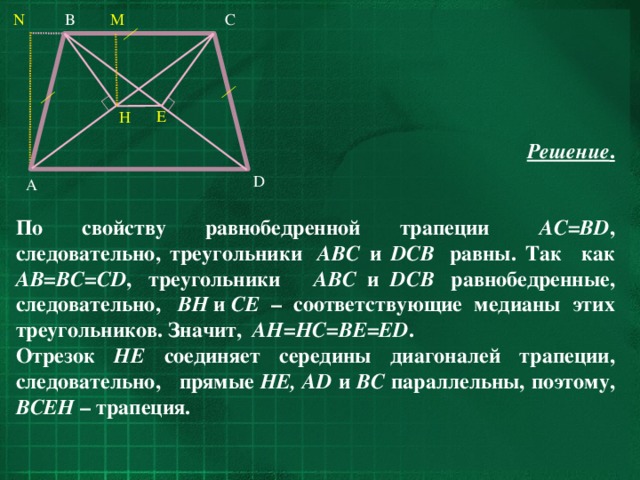
По свойству равнобедренной трапеции AC=BD , следовательно, треугольники ABC и DCB равны. Так как AB=BC=CD , треугольники ABC и DCB равнобедренные, следовательно, BH и CE – соответствующие медианы этих треугольников. Значит, AH=HC=BE=ED .

Отрезок HE соединяет середины диагоналей трапеции, cледовательно, прямые HE, AD и BC параллельны, поэтому, BCEH – трапеция.

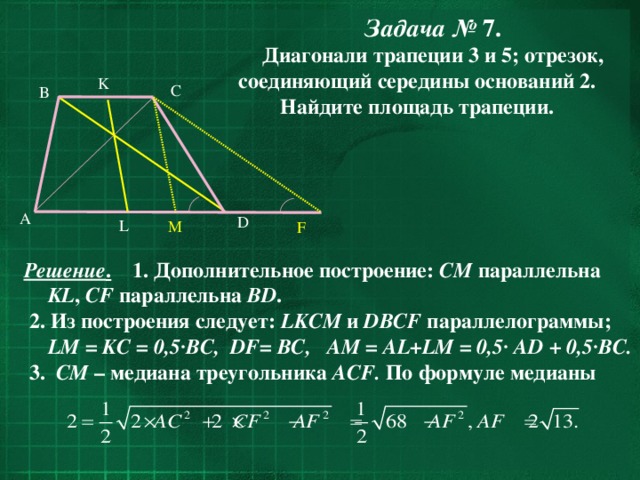
Диагонали трапеции 3 и 5; отрезок, соединяющий середины оснований 2. Найдите площадь трапеции.

2. Из построения следует: LKCM и DBCF параллелограммы; LM = KC = 0,5·BC, DF= BC, AM = AL+LM = 0,5· AD + 0,5·BC.

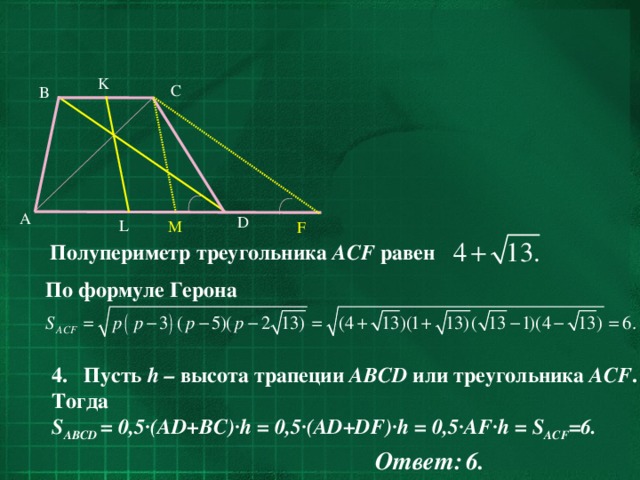
Полупериметр треугольника ACF равен

По формуле Герона

• Задачи для самостоятельного решения

1. Найдите площадь выпуклого четырёхугольника с диагоналями 8 и 5, если отрезки, соединяющие середины противоположных сторон равны. 2. В выпуклом четырёхугольнике ABCТ длина отрезка , соединяющего середины сторон AB и CТ, равна одному метру . Прямые BТ и AC перпендикулярны. Найдите длину отрезка , соединяющего середины диагоналей AC и BТ. 3. На стороне ВC параллелограмма ABCD выбрана точка К. Отрезки АК и ВD пересекаются в точке Р . Площадь параллелограмма ABCD равна 80, а площадь четырёхугольника РКСD равна 31. Найдите площадь треугольника АРD .

• Задачи для самостоятельного решения

4. Диагонали AC и BD трапеции ABCD пересекаются в точке О . Площади треугольников АOD и ВOC равны соответственно 25 см 2 и 16 см 2 . Найдите площадь трапеции. 5. Прямая, параллельная основаниям BC и AD трапеции ABCD , проходит через точку пересечения диагоналей трапеции и пересекает её боковые стороны AB и CD в точках Е и F соответственно. Найдите длину отрезка ЕF , если AD= =12 см, ВC =24 см. 6. В трапеции ABCD ( AD параллельна BC, AD BC ) на диагонали AC выбрана точка Е так, что ВЕ параллельна CD . Площадь треугольника АВC равна 10. Найдите площадь треугольника DЕC .

• Использованные источники

📸 Видео

№478. В выпуклом четырехугольнике диагонали взаимно перпендикулярны. Докажите, что площадьСкачать

ОГЭ Задание 24 Площадь выпуклого четырехугольникаСкачать

Геометрия 8 класс (Урок№14 - Определение подобных треугольников. Отношение площадей подобных фигур.)Скачать

8 класс, 3 урок, ЧетырехугольникСкачать

Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Сможешь найти площадь треугольника? Задача про отношение площадейСкачать

Геометрия 8. Урок 12 - Площадь четырехугольников. Формулы.Скачать

Задача по геометрии № 25 ОГЭ на отношение площадейСкачать

SOS-ГЕОМЕТРИЯ! Отрезки и углы, смежные и вертикальные углы | Математика TutorOnlineСкачать

ВСЯ ГЕОМЕТРИЯ ИЗ ОГЭ ПО МАТЕМАТИКЕ 2023 ЗА 40 МИНУТСкачать

Геометрия 8 класс : Отношение площадей подобных треугольниковСкачать

Площади треугольников с равным углом.Скачать

ТОП-5 ошибок в геометрии | МатематикаСкачать

Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

КАК найти площадь трапеции? Геометрия 8 класс | МатематикаСкачать

Геометрия Диагонали выпуклого четырехугольника ABCD перпендикулярны. Через середины сторон AB и ADСкачать

Подобие треугольников (ч.2) | Математика | TutorOnlineСкачать