Определение . Ненулевой вектор x называется собственным вектором оператора A , если оператор A переводит x в коллинеарный ему вектор, то есть A· x = λ· x . Число λ называется собственным значением или собственным числом оператора A, соответствующим собственному вектору x .
Отметим некоторые свойства собственных чисел и собственных векторов.
1. Любая линейная комбинация собственных векторов x 1, x 2, . x m оператора A , отвечающих одному и тому же собственному числу λ, является собственным вектором с тем же собственным числом.
2. Собственные векторы x 1, x 2, . x m оператора A с попарно различными собственными числами λ1, λ2, …, λm линейно независимы.
3. Если собственные числа λ1=λ2= λm= λ, то собственному числу λ соответствует не более m линейно независимых собственных векторов.
Итак, если имеется n линейно независимых собственных векторов x 1, x 2, . x n, соответствующих различным собственным числам λ1, λ2, …, λn, то они линейно независимы, следовательно, их можно принять за базис пространства Rn. Найдем вид матрицы линейного оператора A в базисе из его собственных векторов, для чего подействуем оператором A на базисные векторы: 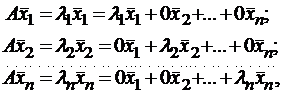

Таким образом, матрица линейного оператора A в базисе из его собственных векторов имеет диагональный вид, причем по диагонали стоят собственные числа оператора A.
Существует ли другой базис, в котором матрица имеет диагональный вид? Ответ на поставленный вопрос дает следующая теорема.
Теорема. Матрица линейного оператора A в базисе < ε i> (i = 1..n) имеет диагональный вид тогда и только тогда, когда все векторы базиса — собственные векторы оператора A.
- Правило отыскания собственных чисел и собственных векторов
- Введение . / Собственные вектора и значения / Литература
- Введение
- Определения и основные факты
- Левый и правый собственный векторы
- Диагонализация матрицы
- Готовые прикладные пакеты для решения проблем собственных векторов и значений
- Собственные числа, собственные векторы матриц и квадратичные формы
- 🎦 Видео
Видео:Собственные векторы и собственные значения матрицыСкачать
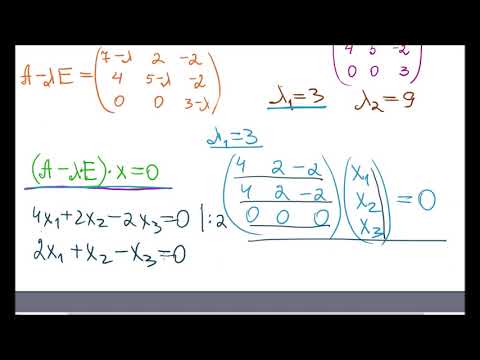
Правило отыскания собственных чисел и собственных векторов
Система (1) имеет ненулевое решение, если ее определитель D равен нулю
Пример №1 . Линейный оператор A действует в R3 по закону A· x =(x1-3x2+4x3, 4x1-7x2+8x3, 6x1-7x2+7x3), где x1, x2, . xn — координаты вектора x в базисе e 1=(1,0,0), e 2=(0,1,0), e 3=(0,0,1). Найти собственные числа и собственные векторы этого оператора.
Решение. Строим матрицу этого оператора:
A· e 1=(1,4,6)
A· e 2=(-3,-7,-7)
A· e 3=(4,8,7) 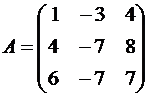
Составляем систему для определения координат собственных векторов:
(1-λ)x1-3x2+4x3=0
x1-(7+λ)x2+8x3=0
x1-7x2+(7-λ)x3=0
Составляем характеристическое уравнение и решаем его:
Пример №2 . Дана матрица 
1. Доказать, что вектор x =(1,8,-1) является собственным вектором матрицы A. Найти собственное число, соответствующее этому собственному вектору.
2. Найти базис, в котором матрица A имеет диагональный вид.
Решение находим с помощью калькулятора.
1. Если A· x =λ· x , то x — собственный вектор
Определение . Симметрической матрицей называется квадратная матрица, в которой элементы, симметричные относительно главной диагонали, равны, то есть в которой ai k =ak i .
Замечания .
- Все собственные числа симметрической матрицы вещественны.
- Собственные векторы симметрической матрицы, соответствующие попарно различным собственным числам, ортогональны.
В качестве одного из многочисленных приложений изученного аппарата, рассмотрим задачу об определении вида кривой второго порядка.
Видео:Собственные значения и собственные векторы матрицы (4)Скачать
Введение . / Собственные вектора и значения / Литература

Видео:Собственные векторы и собственные числа линейного оператораСкачать  ВведениеИз вышеприведенных формул следует также, что для каждого из N собственных значений (не обязательно различных) имеется соответствующий собственный вектор: известно, что если матрица (A — l 1)вырождена, то существует ненулевой вектор, обнуляющий ее при умножении. Если к обоим частям первого выражения добавить t x, то видно, что собственные значения матрицы могут быть изменены на константу t , или сдвинуты, добавлением к матрице единичной, умноженной на эту константу. Собственные вектора при сдвиге не меняются. Сдвиг является важной частью многих алгоритмов вычисления собственных значений. Отсюда также следует, что нулевые собственные значения не имеют специфического смысла: любое собственное значение может быть сдвинуто до нулевого либо нулевое значение — сдвинуто из нуля. Видео:А.7.35 Собственные вектора и собственные значения матрицыСкачать  Определения и основные фактыПри поиске собственных значений матрицы, «эрмитовость» является весьма важной концепцией: все собственные значения эрмитовых матриц действительны. С другой стороны, собственные значения действительных несимметричных матриц могут быть либо действительными, либо парами комплексно — сопряженных чисел. Собственные значения комплексной неэрмитовой матрицы в общем случае комплексные. Концепция «нормальности» важна при поиске собственных векторов. Система собственных векторов нормальной матрицы с невырожденными (несовпадающими) собственными значениями является полным и ортогональным базисом N-мерного векторного пространства. Для нормальной матрицы с вырожденными собственными значениями имеется свобода в определении собственных векторов, соответствующих вырожденным собственным значениям, связанная с заменой их любой линейной комбинацией. Это означает, что мы всегла можем провести процесс ортогонализации Грама — Шмидта и найти полный ортогональный набор собственных векторов, как и в невырожденном случае. Очевидно, что матрица с колонками из ортонормированного множества собственных векторов является унитарной. Для матрицы собственных векторов, полученных из действительной симметричной матрицы, выполняется свойство ортогональности. Если матрица не является нормальной, как, например, любая действительная несимметричная матрица, то в общем случае нельзя отыскать ортонормированный набор собственных векторов, нельзя даже гарантировать ортогональности любой пары из них (кроме редких случаев). В общем случае эти N собственных векторов будут образовывать неортогональный базис в N-мерном пространстве (но не всегда). Если собственные вектора не образуют N-мерный базис, то матрицу будем называть дефектной. Видео:Собственные значения и собственные векторыСкачать  Левый и правый собственный векторыЕсли матрица симметрична, то правый и левый собственные вектора являются транспозицией друг друга, т.е. имеют одни и те же численные компоненты. Точно также, если матрица самосопряженная, то правый и левый вектор взаимно сопряжены по Эрмиту. В общем случае ненормальной матрицы, имеется следующее соотношение. Пусть XR — матрица, состоящая из столбцов правых собственных векторов, XL — из строк левых собственных векторов. По определению собственных векторов имеем: AXR = XRdiag( l 1. l N), XLA = diag( l 1. l N)XL. Умножая первое уравнение слева на XL, а второе справа на XR и вычитая одно из другого, получаем: (XLXR)diag( l 1. l N) = diag( l 1. l N)(XLXR). Это говорит о том, что матрица произведений левых и правых векторов коммутируема с диагональной матрицей из собственных значений. Но в том случае, когда матрица коммутируема с диагональной матрицей, состоящей из несовпадающих элементов, она сама является диагональной. Таким образом, в случае невырожденного набора собственных значений, каждый левый собственный вектор ортогонален всем правым, за исключением соответствующего ему, и наоборот. С помощью нормализации произведение матриц левых и правых векторов всегда можно привести к единичной матрице, для любого невырожденного случая. Если некоторые из собственных значений вырождены, то либо правые, либо левые собственные векторы, соответствующие этим значениям, должны быть линейно скомбинированы между собой, чтобы в итоге образовался ортогональный базис соответственно правых либо левых собственных векторов. Это всегда можно сделать с помощью процедуры ортогонализации Грама — Шмидта. Затем можно настроить нормализацию, чтобы произведение матрицы правых и левых векторов было единичной матрицей. Если этого сделать нельзя (произведение матриц равно нулю), то система собственных векторов неполна. Заметим, что такие неполные системы могут возникать только тогда, когда набор собственных значений вырожден, но не всегда: в частности, неполные системы собственных векторов никогда не возникают в классе нормальных матриц. См. [1] для дальнейших подробностей. В обоих случаях, вырожденном или невырожденном, нормализация произведения матриц правых и левых собственных векторов приводит к следующему результату: матрица, строками которой являются левые собственные векторы — обратна к матрице, столбцами которой являются правые собственные векторы, если обратная матрица существует. Видео:Собственные векторы и собственные числа линейного оператораСкачать  Диагонализация матрицыДля действительных симметричных матриц собственные векторы действительны и ортонормальны, таким образом, трансформирующая матрица является ортогональной. При этом преобразование подобия является ортогональным преобразованием: A -> Z T AZ. Хотя действительные несимметричные матрицы и могут быть диагонализированы «почти во всех» случаях, трансформирующая матрица не обязательно будет действительной. Однако выходит так, что «почти» всю работу в этом случае делает также действительное преобразование подобия. Оно может привести матрицу к системе малых блоков (2 x 2), расположенных по диагонали; все остальные элементы будут нулевыми. Каждый из блоков размера (2 x 2) соответствует комплексно — сопряженной паре собственных чисел. Эта идея будет эксплуатироваться в алгоритмах, помещеных ниже. Главная стратегия почти всех современных методов расчета собственных векторов и собственных значений заключается в том, что матрица приводится к диагональной формы посредством цепочки преобразований подобия: A -> P1 -1 AP1 -> P2 -1 P1 -1 AP1P2 -> P3 -1 P2 -1 P1 -1 AP1P2P3 и т.д. Если эта цепочка приводит в конце концов к диагональной форме, то матрица правых собственных векторов XR будет представлять из себя произведение матриц: XR = P1P2P3. Иногда не требуется проводить подобное преобразование до диагональной формы. Например, если нас интересуют только собственные значения, а не собственные вектора, то достаточно привести к треугольному виду, при котором нулями являются все элементы над диагональю или под ней. В этом случае диагональные элементы преобразованной матрицы уже будут собственными значениями. Имеется два существенно различных подхода к осуществлению указанной стратегии. Часто они хорошо работают в комбинации друг с другом, так что большинство современных методов используют оба из их. Первый подход заключается в построении индивидуальных матриц Pi как явных «элементарных» трансформаторов, расчитанных на специфические задачи, например, для обнуления конкретного внедиагонального элемента (преобразование Якоби) или целого столбца или строки (преобразования Хаусхолдера). В общем случае конечная цепочка подобных преобразований диагонализировать матрицу не может. Имеется выбор: либо использовать конечное число трансформаций для прохода большей части пути к диагонализации (например, приведя к трехдиагональной или Гессенберговской форме), а затем завершить операцию на второй стадии с помощью алгоритмов, которые будут указаны ниже. Либо итерациями свести внедиагональные элементы к пренебрежимо малым. Последний подход концептуально является простейшим и будет обсуждаться в следующем разделе, однако при N больших 10 он является примерно в 5 раз менее эффективен. Другой подход, называемый методами факторизации, более тонкий. Предположим, матрица A может быть разложена в произведение правого FR и левого FL факторов. Тогда = FLFR, или, что эквивалентно, FL -1 = FR. Если мы перемножим эти факторы в обратном порядке и используем вышенаписанное тождество, то будем иметь FRFL = FL -1 AFL, что сразу распознается как преобразование подобия матрицы A с трансформирующей матрицей FL. Эту идею использует метод QR-разложения матрицы. Методы факторизации также не дают сходимость за конечное число шагов. Но лучшие из них сходятся быстро и надежно, и при использовании хорошего начального состояния матрицы, первично преобразованной элементарными операциями, являются главным выбором. Видео:Собственные значения и собственные векторы. ТемаСкачать  Готовые прикладные пакеты для решения проблем собственных векторов и значенийПочти все готовые программы, использующиеся сейчас, восходят к алгоритмам, опубликованным в Handbook for Automatic Computation, by Wilkinson & Reinsch, Vol. II, Linear Algebra [2]. Эта великолепная подборка работ различных авторов является своего рода Библией в данной области. Общедоступным пакетом, осуществляющим алгоритмы из этой книги на Фортране, является EISPACK [3]. Программы в этой главе нашей книги являются переводами программ из Handbook или EISPACK, так что понимание приведет вас в значительной мере к пониманию того, как эти канонические пакеты составляются. Пакеты IMSL [4] и NAG [5] также воспроизводят в основном алгоритмы из Handbook, на Фортране. «Хороший пакет» по проблеме собственных векторов должен быть представлен отдельными программами, либо отдельными путями цепочек программ для каждой из следующих задач:
Целью этого разделения является экономия компьютерного времени и ресурсов; нет смысла вычислять собственные векторы, если они не нужны. Часто интересуются только векторами, соответствующими самым большим собственным значениям, или самым большим по модулю, или только отрицательным. В этом случае метод, который используется для вычисления «некоторых» собственных векторов, обычно более эффективен, чем метод для всех, если вам нужно не более четверти от общего количества. Хороший пакет также представляет отдельные пути решения для следующих типов матриц:
Опять, целью этого разделения является экономия времени и ресурсов с помощью использования наименее генерализированной процедуры. В настоящей главе мы представим программы для следующих случаев:
Также будет рассмотрено, каким образом получить некоторые собственные векторы несимметричной матрицы методом обратной итерации. Видео:Матрицы и векторыСкачать  Собственные числа, собственные векторы матриц и квадратичные формыПроблема собственных чисел играет существенную роль не только в линейной алгебре, но и в других разделах математики, а также во многих прикладных областях (в менеджменте, психологии, юриспруденции). Пусть задана квадратная матрица А размера (n X п), элементами которой являются действительные числа (R) и вектор неизвестных X размера (n X 1): Предположим, что X — это некоторое неизвестное действительное число. Если X и ненулевой вектор X удовлетворяют уравнению то X называется собственным числом или собственным значением матрицы А, а X — собственным вектором этой же матрицы, соответствующим X. Преобразуем уравнение (2.15) к следующему виду: где Е — единичная матрица. называется характеристической матрицей. Так как по условию вектор неизвестных X не равен нулю, то среди его координат х , х2, . хп должна быть хотя бы одна ненулевая. А для того, чтобы система линейных однородных уравнений (2.16) имела ненулевое решение, необходимо и достаточно, чтобы определитель этой системы был равен нулю (это следует из теоремы Кронекера-Капелли). Число X = Xfc, где к = 1, п будет собственным числом только в том случае, если матрица (ХкЕ -А) — вырожденная. Уравнение (2.17) называется характеристическим уравнением матрицы А и представляет собой алгебраическое уравнение степени п относительно X: Уравнение (2.18) имеет п корней Xv Х2, Хп. Множество всех корней уравнения (2.18) называется спектром матрицы А. Заметим, что уравнение det (А — ХЕ) = 0 имеет те же корни, что и уравнение (2.17), т. е. Каждому собственному значению спектра матрицы А ставится в соответствие собственный вектор, определенный с точностью до скалярного множителя. Если Хк есть кратный корень характеристического уравнения, то для произвольной квадратной матрицы число соответствующих собственных векторов может быть не равно кратности корня. С геометрической точки зрения собственный вектор определяет в пространстве некоторое направление (прямую, проходящую через начало координат), которое в результате преобразования не изменяется и вдоль которого пространство испытывает растяжение или сжатие в X раз. Полином Х п + р^” -1 + . + рп = 0 называют характеристическим полиномом. Коэффициенты рк (k = 1, п) можно вычислить по следующим рекуррентным формулам [57]: Здесь SpA = S акк — след матрицы (сумма элементов, стоя- щих на главной диагонали матрицы А). Заметим, что р = (-1)” X X det А. При отыскании собственных чисел даже для матриц невысокого порядка неизбежно большое количество вычислений. Для общего случая нельзя предложить оптимальный способ нахождения собственных чисел и собственных векторов матрицы. Рассмотрим случай, когда собственные числа находятся сразу исходя из вида матрицы (исходная матрица либо диагональная, либо верхняя или нижняя треугольная). В этом случае собственные числа 2. п совпадают с элементами главной диагонали исходной матрицы ап, а22. апп. Пусть задана верхняя треугольная матрица А размера (n X п): Отсюда видно, что собственные числа равны: С появлением ЭВМ получили распространение итерационные методы нахождения собственных чисел, которые не используют вычисление характеристического полинома. К этим способам относятся: степенной метод, метод обратных итераций, QR-алгоритм, метод вращений Якоби, QL-алгоритм и др. Причем применение конкретного итерационного метода зависит от вида исходной матрицы А [4]. Теперь рассмотрим конкретные примеры. Пример 2.8. Дана матрица А размера (3 X 3) Найти собственные числа и собственные векторы матрицы А. Из условия задачи видно, что матрица А является верхней треугольной матрицей. Поэтому собственными числами данной матрицы будут элементы ее главной диагонали Теперь найдем соответствующие найденным собственным числам собственные векторы. Для этого мы используем уравнение (2.16). Для Х1 = -4 получаем Далее раскроем матричное уравнение (2.20) В результате получим Так как матрица этой системы вырождена, то она имеет ненулевые решения, которые имеют вид: т. е. получены искомые собственные вектора для Для Х2 = Х3 = 1 получаем ил* В результате получаем т. е. это уравнение имеет ненулевые решения, которые и будут искомыми собственными векторами для 2. Эти решения запишем в виде Пример 2.9. Дана матрица А размера (2 X 2). Найти собственные числа и собственные матрицы А Запишем характеристическое уравнение (2.17) для данного случая Теперь найдем собственные векторы исходной матрицы А, соответствующие .1 = 1 и Х2 = -4. В подробной записи получим Так как определитель полученной матрицы равен нулю, то она имеет ненулевые решения, которые и являются собственными векторами Xv которые мы и находим Из первого уравнения системы получаем х2 = 2xv Из второго уравнения системы получаем х2 = 2xv т. е. она имеет бесконечное множество решений. И искомый собственный вектор Xj будет иметь вид Аналогично, для Х2 = -4 находим В заключение приведем два полезных правила [38]: 1) сумма собственных чисел матрицы А равна следу этой матрицы, т. е. 2) произведение собственных чисел матрицы А равно определителю этой матрицы Кратко рассмотрим квадратичные формы. Квадратичной формой называется однородный многочлен второй степени от нескольких пременных. Обозначим их xv х2, . х . Квадратичную форму в общем виде можно записать так: В качестве примера рассмотрим квадратичную форму трех переменных: Введем обозначения: Тогда квадратичная форма примет вид Дополнительно вводим симметричную матрицу В, вектор X. В этом случае квадратичная форма примет вид Последняя формула представляет собой матрично-векторный вид квадратичной формы. А в общем случае получим: где Ь..— коэффициенты при х 2 для всех i = 1, 2, n, a b’j = Ц< равны полусуммам коэффициентов при элементах, содержащих произведения х. х. и х. х< при всех г, j = 1, 2,п, г ^ j. Матрица В является матрицей квадратичной формы. В качестве примера запишем в матрично-векторном виде квадратичную форму В данном случае получаем: Матрица данной квадратичной формы принимает вид 🎦 ВидеоЛинал 1.8 Собственные векторы и собственные числаСкачать  Собственные векторы и собственные значенияСкачать  1. Матрицы ( основные понятия, виды матриц )Скачать  Айгенвектора и айгензначения | Сущность Линейной Алгебры, глава 10Скачать  7 4 Собственные векторы и собственные значенияСкачать  Собственные значения и собственные векторы линейного оператораСкачать  Собственные значения матрицыСкачать  Что такое векторы и матрицы? Душкин объяснитСкачать  Диагональный вид матрицы. Приведение матрицы к диагональному виду. Собственные векторыСкачать  Матрицы: виды и действия над ними | Высшая математика | Линейная алгебра | TutorOnlineСкачать  Собственные числа, собственные, присоединенные векторы. Матрица оператора в базисе...Скачать  14.1 Собственные значения и собственные векторы линейного оператора.Скачать  |
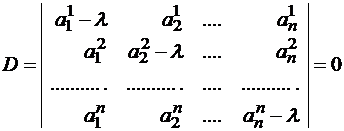
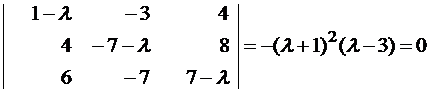








































 А ее матрично-векторная запись такова:
А ее матрично-векторная запись такова: