Еще одной из задач, помимо решения систем линейных алгебраических уравнений, часто возникающих при осуществлении практической деятельности — это вычисление собственных значений матрицы и соответствующих им собственных векторов. Проблема определения собственных чисел и собственных векторов возникает при анализе схем и конструкций, характеризующихся малыми смещениями от положения равновесия, при анализе устойчивости численных схем, в теории механических и электрических колебаний и т. д.
Различают полную, когда необходимо найти все значения, и частичную, когда необходимо найти часть значений, проблему собственных значений. Задачу нахождения собственных значений и собственных векторов часто называют второй задачей линейной алгебры.
Собственными числами действительной квадратной матрицы А называют числа X, в общем случае комплексные, при которых определитель матрицы:
Иными словами, собственное число X матрицы А должно удовлетворять уравнению:
- Метод непосредственного развертывания
- Методы решения задач о собственных значениях и векторах матриц
- Постановка задачи
- Метод непосредственного развертывания
- Алгоритм метода непосредственного развертывания
- Метод итераций для нахождения собственных значений и векторов
- Алгоритм метода итераций
- Метод вращений для нахождения собственных значений
- Алгоритм метода вращений
- Курсовая работа: Собственные значения.
- 💥 Видео
Видео:Собственные векторы и собственные числа линейного оператораСкачать

Метод непосредственного развертывания
Полную проблему собственных значений для матриц невысокого порядка (п $ 10) можно решить методом непосредственного развертывания.
Если раскрыть определитель из (3.10), то он превратится в полином степени п относительно X:
где п — размер матрицы А, а коэффициенты р^ зависят только от значений элементов матрицы А. Уравнение (3.10) примет вид:
Данное уравнение еще называется характеристическим уравнением. Таким образом, задача о поиске собственных чисел матрицы размера пх« сводится к поиску корней полинома степени п.
В общем случае полином (3.11) может быть представлен в виде произведения:
где X, — z-ый корень полинома; «// — кратность корня X,; А? —число различных корней.
В математике есть т. н. основная теорема алгебры, которая утверждает: всякий полином степени п имеет в поле комплексных чисел ровно п корней, причем каждый корень считается столько раз, какова его кратность. Это означает, что тх + т2 + . + тк = п.
Задача поиска корней полинома в аналитическом виде решена лишь для п 4 возможен только их численный поиск.
С собственным числом матрицы связано понятие «собственный вектор». Собственным вектором матрицы А, соответствующим собственному числу X,, называют вектор tj, для которого справедливо соотношение:
Допустим, что матрица А имеет п различных собственных чисел и соответственно п собственных векторов. Составим матрицу Т, столбцы которой образованы векторами
и запишем уравнения (3.14) в матричной форме:
к , 1 $ j $ п, причем j может быть любой. Шаг итерации к полагаем равным 1.
Шаг 3. Вычисляем Х/ +| — А х Х к .
Шаг 4. Вычисляем k| +1 = x^/x^(.y
Шаг 5. вычисляем А = |Xj’ +1 — Х*|. Если А +| , в противном случае полагаем к = к + 1 и переходим к шагу 3.
Процесс приближений Х к = А * А,*’ -1 = А х А к
‘ х Xf сходится при к —> оо, и Х к стремится к собственному вектору А).
Видео:Собственные векторы и собственные значения матрицыСкачать

Методы решения задач о собственных
значениях и векторах матриц
Видео:Собственные значения и собственные векторы матрицы (4)Скачать

Постановка задачи
Пусть [math]A[/math] — действительная числовая квадратная матрица размера [math](ntimes n)[/math] . Ненулевой вектор [math]X= bigl(x_1,ldots,x_nbigr)^T[/math] размера [math](ntimes1)[/math] , удовлетворяющий условию
называется собственным вектором матрицы [math]A[/math] . Число [math]lambda[/math] в равенстве (2.1) называется собственным значением. Говорят, что собственный вектор [math]X[/math] соответствует (принадлежит) собственному значению [math]lambda[/math] .
Равенство (2.1) равносильно однородной относительно [math]X[/math] системе:
Система (2.2) имеет ненулевое решение для вектора [math]X[/math] (при известном [math]lambda[/math] ) при условии [math]|A-lambda E|=0[/math] . Это равенство есть характеристическое уравнение:
где [math]P_n(lambda)[/math] — характеристический многочлен n-й степени. Корни [math]lambda_1, lambda_2,ldots,lambda_n[/math] характеристического уравнения (2.3) являются собственными (характеристическими) значениями матрицы [math]A[/math] , а соответствующие каждому собственному значению [math]lambda_i,
i=1,ldots,n[/math] , ненулевые векторы [math]X^i[/math] , удовлетворяющие системе
являются собственными векторами.
Требуется найти собственные значения и собственные векторы заданной матрицы. Поставленная задача часто именуется второй задачей линейной алгебры.
Проблема собственных значений (частот) возникает при анализе поведения мостов, зданий, летательных аппаратов и других конструкций, характеризующихся малыми смещениями от положения равновесия, а также при анализе устойчивости численных схем. Характеристическое уравнение вместе с его собственными значениями и собственными векторами является основным в теории механических или электрических колебаний на макроскопическом или микроскопическом
уровнях.
Различают полную и частичную проблему собственных значений, когда необходимо найти весь спектр (все собственные значения) и собственные векторы либо часть спектра, например: [math]rho(A)= max_|lambda_i(A)|[/math] и [math]min_|lambda_i(A)|[/math] . Величина [math]rho(A)[/math] называется спектральным радиусом .
1. Если для собственного значения [math]lambda_i[/math] — найден собственный вектор [math]X^i[/math] , то вектор [math]mu X^i[/math] , где [math]mu[/math] — произвольное число, также является собственным вектором, соответствующим этому же собственному значению [math]lambda_i[/math] .
2. Попарно различным собственным значениям соответствуют линейно независимые собственные векторы; k-кратному корню характеристического уравнения соответствует не более [math]k[/math] линейно независимых собственных векторов.
3. Симметрическая матрица имеет полный спектр [math]lambda_i,
i=overline[/math] , действительных собственных значений; k-кратному корню характеристического уравнения симметрической матрицы соответствует ровно [math]k[/math] линейно независимых собственных векторов.
4. Положительно определенная симметрическая матрица имеет полный спектр действительных положительных собственных значений.
Видео:Собственные значения и собственные векторы. ТемаСкачать

Метод непосредственного развертывания
Полную проблему собственных значений для матриц невысокого порядка [math](nleqslant10)[/math] можно решить методом непосредственного развертывания. В этом случае будем иметь
Уравнение [math]P_n(lambda)=0[/math] является нелинейным (методы его решения изложены в следующем разделе). Его решение дает [math]n[/math] , вообще говоря, комплексных собственных значений [math]lambda_1,lambda_2,ldots,lambda_n[/math] , при которых [math]P_n(lambda_i)=0
(i=overline)[/math] . Для каждого [math]lambda_i[/math] может быть найдено решение однородной системы [math](A-lambda_iE)X^i=0,
i=overline[/math] . Эти решения [math]X^i[/math] , определенные с точностью до произвольной константы, образуют систему [math]n[/math] , вообще говоря, различных векторов n-мерного пространства. В некоторых задачах несколько этих векторов (или все) могут совпадать.
Видео:Метод простой итерации Пример РешенияСкачать

Алгоритм метода непосредственного развертывания
1. Для заданной матрицы [math]A[/math] составить характеристическое уравнение (2.5): [math]|A-lambda E|=0[/math] . Для развертывания детерминанта [math]|A-lambda E|[/math] можно использовать различные методы, например метод Крылова, метод Данилевского или другие методы.
2. Решить характеристическое уравнение и найти собственные значения [math]lambda_1, lambda_2, ldots,lambda_n[/math] . Для этого можно применить методы, изложенные далее.
3. Для каждого собственного значения составить систему (2.4):
и найти собственные векторы [math]X^i[/math] .
Замечание. Каждому собственному значению соответствует один или несколько векторов. Поскольку определитель [math]|A-lambda_iE|[/math] системы равен нулю, то ранг матрицы системы меньше числа неизвестных: [math]operatorname(A-lambda_iE)=r и в системе имеется ровно [math]r[/math] независимых уравнений, а [math](n-r)[/math] уравнений являются зависимыми. Для нахождения решения системы следует выбрать [math]r[/math] уравнений с [math]r[/math] неизвестными так, чтобы определитель составленной системы был отличен от нуля. Остальные [math](n-r)[/math] неизвестных следует перенести в правую часть и считать параметрами. Придавая параметрам различные значения, можно получить различные решения системы. Для простоты, как правило, попеременно полагают значение одного параметра равным 1, а остальные равными 0.
Пример 2.1. Найти собственные значения и собственные векторы матрицы [math]Ain mathbb^[/math] , где [math]A=begin3&-2\-4&1end[/math] .
1. Запишем уравнение (2.5): [math]|A-lambda E|= begin3-lambda&-2\-4& 1-lambda end= lambda^2-4 lambda-5=0[/math] , отсюда получаем характеристическое уравнение [math]P_2(lambda)equiv lambda^2-4 lambda-5=0[/math] .
2. Находим его корни (собственные значения): [math]lambda_1=5,
3. Составим систему [math](A-lambda_iE)X^i=0,
i=1,2[/math] , для каждого собственного
значения и найдем собственные векторы:
Отсюда [math]x_1^1=-x_2^1[/math] . Если [math]x_2^1=mu[/math] , то [math]x_1^1=-mu[/math] . В результате получаем [math]X^1= bigl^T= bigl^T[/math] .
Для [math]lambda_2=-1[/math] имеем
Отсюда [math]x_2^2=2x_1^2[/math] . Если [math]x_1^2=mu[/math] , то [math]x_2^2=2mu[/math] . В результате получаем [math]X^2= bigl^T= bigl^T[/math] , где [math]mu[/math] — произвольное действительное число.
Пример 2.2. Найти собственные значения и собственные векторы матрицы [math]A= begin2&-1&1\-1&2&-1\0&0&1end[/math] .
1. Запишем характеристическое уравнение (2.5):
2. Корни характеристического уравнения: [math]lambda_=1[/math] (кратный корень), [math]lambda_3=3[/math] — собственные значения матрицы.
3. Найдем собственные векторы.
Для [math]lambda_=1[/math] запишем систему [math](A-lambda_E)cdot X^=0colon[/math]
Поскольку [math]operatorname(A-lambda_E)=1[/math] , в системе имеется одно независимое уравнение
x_3^=3[/math] , получаем [math]x_1^=1[/math] и собственный вектор [math]X^1= begin1&1&0end^T[/math] .
x_3^=1[/math] , получаем [math]x_1^=-1[/math] и другой собственный вектор [math]X^2= begin-1&0&1end^T[/math] . Заметим, что оба собственных вектора линейно независимы.
Для собственного значения [math]lambda_3=3[/math] запишем систему [math](A-lambda_3E)cdot X^3=0colon[/math]
Поскольку [math]operatorname(A-lambda_3E)=2[/math] , то выбираем два уравнения:
x_1^3=-x_2^3[/math] . Полагая [math]x_2^3=1[/math] , получаем [math]x_1^3=-1[/math] и собственный вектор [math]X^3=begin-1&1&0 end^T[/math] .
Видео:Собственные значения и собственные векторыСкачать

Метод итераций для нахождения собственных значений и векторов
Для решения частичной проблемы собственных значений и собственных векторов в практических расчетах часто используется метод итераций (степенной метод). На его основе можно определить приближенно собственные значения матрицы [math]A[/math] и спектральный радиус [math]rho(A)= max_bigl|lambda_i(A)bigr|[/math] .
Пусть матрица [math]A[/math] имеет [math]n[/math] линейно независимых собственных векторов [math]X^i,
i=1,ldots,n[/math] , и собственные значения матрицы [math]A[/math] таковы, что
Видео:А.7.35 Собственные вектора и собственные значения матрицыСкачать

Алгоритм метода итераций
1. Выбрать произвольное начальное (нулевое) приближение собственного вектора [math]X^[/math] (второй индекс в скобках здесь и ниже указывает номер приближения, а первый индекс без скобок соответствует номеру собственного значения). Положить [math]k=0[/math] .
lambda_1^= frac<x_i^><x_i^>[/math] , где [math]i[/math] — любой номер [math]1leqslant ileqslant n[/math] , и положить [math]k=1[/math] .
4. Найти [math]lambda_1^= frac<x_i^><x_i^>[/math] , где [math]x_i^, x_i^[/math] — соответствующие координаты векторов [math]X^[/math] и [math]X^[/math] . При этом может быть использована любая координата с номером [math]i,
1leqslant ileqslant n[/math] .
5. Если [math]Delta= bigl|lambda_1^- lambda_1^bigr|leqslant varepsilon[/math] , процесс завершить и положить [math]lambda_1cong lambda_1^[/math] . Если varepsilon»>[math]Delta>varepsilon[/math] , положить [math]k=k+1[/math] и перейти к пункту 3.
1. Процесс последовательных приближений
сходится, т.е. при [math]xtoinfty[/math] вектор [math]X^[/math] стремится к собственному вектору [math]X^1[/math] . Действительно, разложим [math]X^[/math] по всем собственным векторам: [math]textstyle<X^= sumlimits_^ c_iX^i>[/math] . Так как, согласно (2.4), [math]AX^i= lambda_iX^i[/math] , то
При большом [math]k[/math] дроби [math]<left(fracright)!>^k, ldots, <left(fracright)!>^k[/math] малы и поэтому [math]A^kX^= c_1lambda_1^kX^1[/math] , то есть [math]X^to X^1[/math] при [math]ktoinfty[/math] . Одновременно [math]lambda_1= limlimits_ frac<x_^><x_^>[/math] .
2. Вместо применяемой в пункте 4 алгоритма формулы для [math]lambda_1^[/math] можно взять среднее арифметическое соответствующих отношений для разных координат.
3. Метод может использоваться и в случае, если наибольшее по модулю собственное значение матрицы [math]A[/math] является кратным, т.е.
4. При неудачном выборе начального приближения [math]X^[/math] предел отношения [math]frac<x_i^><x_i^>[/math] может не существовать. В этом случае следует задать другое начальное приближение.
5. Рассмотренный итерационный процесс для [math]lambda_1[/math] сходится линейно, с параметром [math]c=frac[/math] и может быть очень медленным. Для его ускорения используется алгоритм Эйткена.
6. Если [math]A=A^T[/math] (матрица [math]A[/math] симметрическая), то сходимость процесса при определении [math]rho(A)[/math] может быть ускорена.
7. Используя [math]lambda_1[/math] , можно определить следующее значение [math]lambda_2[/math] по формуле [math]lambda_2= frac<x_i^- lambda_1 x_i^><x_i^- lambda_1 x_i^>
(i=1,2,ldots,n)[/math] . Эта формула дает грубые значения для [math]lambda_2[/math] , так как значение [math]lambda_1[/math] является приближенным. Если модули всех собственных значений различны, то на основе последней формулы можно вычислять и остальные [math]lambda_j
8. После проведения нескольких итераций рекомендуется «гасить» растущие компоненты получающегося собственного вектора. Это осуществляется нормировкой вектора, например, по формуле [math]frac<X^><|X^|_1>[/math] .
Пример 2.3. Для матрицы [math]A=begin5&1&2\ 1&4&1\ 2&1&3 end[/math] найти спектральный радиус степенным методом с точностью [math]varepsilon=0,,1[/math] .
1. Выбирается начальное приближение собственного вектора [math]X^= begin 1&1&1 end^T[/math] . Положим [math]k=0[/math] .
5. Так как varepsilon»>[math]bigl|lambda_1^- lambda_1^bigr|= 0,!75> varepsilon[/math] , то процесс необходимо продолжить. Результаты вычислений удобно представить в виде табл. 10.10.
Точность по достигнута на четвертой итерации. Таким образом, в качестве приближенного значения [math]lambda_1[/math] берется 6,9559, а в качестве собственного вектора принимается [math]X^1= begin 2838& 1682& 1888end^T[/math] .
Так как собственный вектор определяется с точностью до постоянного множителя, то [math]X^1[/math] лучше пронормировать, т.е. поделить все его компоненты на величину нормы. Для рассматриваемого примера получим
Согласно замечаниям, в качестве собственного значения [math]lambda_1[/math] матрицы можно взять не только отношение
а также их среднее арифметическое [math]fracapprox 6,!8581[/math] .
Пример 2.4. Найти максимальное по модулю собственное значение матрицы [math]A=begin2&-1&1\ -1&2&-1\ 0&0&3 end[/math] и соответствующий собственный вектор.
1. Зададим начальное приближение [math]X^= begin1&-1&1 end^T[/math] и [math]varepsilon=0,!0001[/math] .
Выполним расчеты согласно методике (табл. 10.11).
В результате получено собственное значение [math]lambda_1cong 3,!00003[/math] и собственный вектор [math]X^1= begin 88573&-88573&1end^T[/math] или после нормировки
Видео:А.7.40 Метод Якоби поиска собственных векторов и значений симметричных матрицСкачать

Метод вращений для нахождения собственных значений
Метод используется для решения полной проблемы собственных значений симметрической матрицы и основан на преобразовании подобия исходной матрицы [math]Ainmathbb^[/math] с помощью ортогональной матрицы [math]H[/math] .
Напомним, что две матрицы [math]A[/math] и [math]A^[/math] называются подобными ( [math]Asim A^[/math] или [math]A^sim A[/math] ), если [math]A^=H^AH[/math] или [math]A=HA^H^[/math] , где [math]H[/math] — невырожденная матрица.
В методе вращений в качестве [math]H[/math] берется ортогональная матрица, такая, что [math]HH^=H^H=E[/math] , т.е. [math]H^=H^[/math] . В силу свойства ортогонального преобразования евклидова норма исходной матрицы [math]A[/math] не меняется. Для преобразованной матрицы [math]A^[/math] сохраняется ее след и собственные значения [math]lambda_icolon[/math]
[math]operatorname
При реализации метода вращений преобразование подобия применяется к исходной матрице [math]A[/math] многократно:
Формула (2.6) определяет итерационный процесс, где начальное приближение [math]A^=A[/math] . На k-й итерации для некоторого выбираемого при решении задачи недиагонального элемента [math]a_^,
ine j[/math] , определяется ортогональная матрица [math]H^[/math] , приводящая этот элемент [math]a_^[/math] (а также и [math]a_^[/math] ) к нулю. При этом на каждой итерации в качестве [math]a_^[/math] выбирается наибольший по модулю. Матрица [math]H^[/math] называемая матрицей вращения Якоби, зависит от угла [math]varphi^[/math] и имеет вид
В данной ортогональной матрице элементы на главной диагонали единичные, кроме [math]h_^= cosvarphi^[/math] и [math]h_^=cosvarphi^[/math] , а остальные элементы нулевые, за исключением [math]h_^=-sinvarphi^[/math] , [math]h_^=sinvarphi^[/math] ( [math]h_[/math] -элементы матрицы [math]H[/math] ).
Угол поворота [math]varphi^[/math] определяется по формуле
где [math]|2varphi^|leqslant frac,
i ( [math]a_[/math] выбирается в верхней треугольной наддиагональной части матрицы [math]A[/math] ).
В процессе итераций сумма квадратов всех недиагональных элементов [math]sigms(A^)[/math] при возрастании [math]k[/math] уменьшается, так что [math]sigms(A^) . Однако элементы [math]a_^[/math] приведенные к нулю на k-й итерации, на последующей итерации немного возрастают. При [math]ktoinfty[/math] получается монотонно убывающая ограниченная снизу нулем последовательность sigma(A^)> ldots> sigma(A^)>ldots»>[math]sigma(A^)> sigma(A^)> ldots> sigma(A^)>ldots[/math] . Поэтому [math]sigma(A^)to0[/math] при [math]ktoinfty[/math] . Это и означает сходимость метода. При этом [math]A^to Lambda= operatorname(lambda_1,ldots,lambda_n)[/math] .
Замечание. В двумерном пространстве с введенной в нем системой координат [math]Oxy[/math] с ортонормированным базисом [math]<vec,vec>[/math] матрица вращения легко получается из рис. 2.1, где система координат [math]Ox’y'[/math] повернута на угол [math]varphicolon[/math]
Таким образом, для компонент [math]vec,’,, vec,'[/math] будем иметь [math]bigl(vec,’,vec,’bigr)= bigl(vec,vecbigr)cdot! begin cos varphi&-sin varphi\ sin varphi& cos varphiend[/math] . Отсюда следует, что в двумерном пространстве матрица вращения имеет вид [math]H= begin cos varphi&-sin varphi\ sin varphi& cos varphiend[/math] . Отметим, что при [math]n=2[/math] для решения задачи требуется одна итерация.
Видео:Собственные векторы и собственные значенияСкачать

Алгоритм метода вращений
1. Положить [math]k=0,
A^=A[/math] и задать 0″>[math]varepsilon>0[/math] .
2. Выделить в верхней треугольной наддиагональной части матрицы [math]A^[/math] максимальный по модулю элемент [math]a_^,
Если [math]|a_^|leqslant varepsilon[/math] для всех [math]ine j[/math] , процесс завершить. Собственные значения определяются по формуле [math]lambda_i(A^)=a_^,
Собственные векторы [math]X^i[/math] находятся как i-e столбцы матрицы, получающейся в результате перемножения:
Если varepsilon»>[math]bigl|a_^bigr|>varepsilon[/math] , процесс продолжается.
3. Найти угол поворота по формуле [math]varphi^= frac operatorname frac<2a_^><a_^-a_^>[/math] .
4. Составить матрицу вращения [math]H^[/math] .
5. Вычислить очередное приближение [math]A^= bigl(H^bigr)^T A^ H^[/math] .Положить [math]k=k+1[/math] и перейти к пункту 2.
1. Используя обозначение [math]overline
_k= frac<2a_^><a_^-a_^>[/math] , можно в пункте 3 алгоритма вычислять элементы матрицы вращения по формулам
2. Контроль правильности выполнения действий по каждому повороту осуществляется путем проверки сохранения следа преобразуемой матрицы.
3. При [math]n=2[/math] для решения задачи требуется одна итерация.
Пример 2.5. Для матрицы [math]A=begin 2&1\1&3 end[/math] методом вращений найти собственные значения и собственные векторы.
1. Положим [math]k=0,
2°. Выше главной диагонали имеется только один элемент [math]a_=a_=1[/math] .
3°. Находим угол поворота матрицы по формуле (2.7), используя в расчетах 11 цифр после запятой в соответствии с заданной точностью:
4°. Сформируем матрицу вращения:
5°. Выполним первую итерацию:
Очевидно, след матрицы с заданной точностью сохраняется, т.е. [math]sum_^a_^= sum_^a_^=5[/math] . Положим [math]k=1[/math] и перейдем к пункту 2.
2. Максимальный по модулю наддиагональный элемент [math]|a_|= 4,!04620781325cdot10^ . Для решения задачи (подчеркнем, что [math]n=2[/math] ) с принятой точностью потребовалась одна итерация, полученную матрицу можно считать диагональной. Найдены следующие собственные значения и собственные векторы:
Пример 2.6. Найти собственные значения и собственные векторы матрицы [math]A=begin5&1&2\ 1&4&1\ 2&1&3 end[/math] .
1. Положим [math]k=0,
2°. Выделим максимальный по модулю элемент в наддиагональнои части: [math]a_^=2[/math] . Так как varepsilon=0,!001″>[math]a_=2> varepsilon=0,!001[/math] , то процесс продолжается.
3°. Находим угол поворота:
4°. Сформируем матрицу вращения: [math]H^= begin0,!85065&0&-0,!52573\ 0&1&0\ 0,!52573&0&0,!85065 end[/math] .
5°. Выполним первую итерацию: [math]A^= bigl(H^bigr)^T A^H^= begin 6,!236&1,!376&2,!33cdot10^\ 1,!376&4&0,!325\ 2,!33cdot10^&0,!325&1,!764 end[/math] . Положим [math]k=1[/math] и перейдем к пункту 2.
2(1). Максимальный по модулю наддиагональный элемент [math]a_^=1,!376[/math] . Так как varepsilon=0,!001″>[math]a_^> varepsilon=0,!001[/math] , процесс продолжается.
3(1). Найдем угол поворота:
4(1). Сформируем матрицу вращения: [math]H^= begin 0,!902937&-0,!429770&0\ 0,!429770&0,!902937&0\ 0&0&1 end[/math] .
5(1). Выполним вторую итерацию: [math]A^= bigl(H^bigr)^T A^H^= begin 6,!891& 2,!238cdot10^&0,!14\ 2,!238cdot10^& 3,!345&0,!293\ 0,!14&0,!293&1,!764 end[/math] . Положим [math]k=2[/math] и перейдем к пункту 2.
2(2). Максимальный по модулю наддиагональный элемент varepsilon=0,!001″>[math]a_^=0,!293> varepsilon=0,!001[/math] .
3(2). Найдем угол поворота:
4(2). Сформируем матрицу вращения [math]H^= begin1&0&0\ 0&0,!9842924& -0,!1765460\ 0& 0,!1765460& 0,!9842924end[/math] .
5(2). Выполним третью итерацию и положим [math]k=3[/math] и перейдем к пункту 2:
2(3). Максимальный по модулю наддиагональный элемент varepsilon»>[math]a_^= 0,!138>varepsilon[/math] .
3(3). Найдем угол поворота:
4(3). Сформируем матрицу вращения: [math]H^= begin 0,!999646&0&-0,!026611\ 0&1&0\ 0,!026611&0&0,!999646 end[/math] .
5(3). Выполним четвертую итерацию и положим [math]k=4[/math] и перейдем к пункту 2:
2(4). Так как varepsilon»>[math]a_^=0,!025>varepsilon[/math] , процесс повторяется
3(4). Найдем угол поворота
4(4). Сформируем матрицу вращения: [math]H^= begin 0,!9999744&-0,!0071483&0\ 0,!0071483&0,!9999744&0\ 0&0&1 end[/math] .
5(4). Выполним пятую итерацию и положим [math]k=5[/math] и перейдем к пункту 2:
2(5). Так как наибольший по модулю наддиагональный элемент удовлетворяет условию [math]bigl|-6,!649cdot10^bigr| , процесс завершается.
Собственные значения: [math]lambda_1cong a_^= 6,!895,,
lambda_3cong a_^=1,!707,,[/math] . Для нахождения собственных векторов вычислим
X^3=begin-0,!473\-0,!171\0,!864 end[/math] или после нормировки
Видео:7 4 Собственные векторы и собственные значенияСкачать

Курсовая работа: Собственные значения.
| Название: Собственные значения. Раздел: Рефераты по математике Тип: курсовая работа Добавлен 20:07:25 17 февраля 2003 Похожие работы Просмотров: 1164 Комментариев: 26 Оценило: 2 человек Средний балл: 5 Оценка: неизвестно Скачать | |||||||||||||||||||||||||||||||||||||||||||||||
| 1 | 4 | 5 |
| 4 | 3 | 7 |
| 5 | 7 | 2 |
является примером симметричной.
2. Матрица A называется трехдиагональной, если все ее элементы, кроме элементов главной и примыкающих к ней диагоналей, равны нулю. В общем случае трехдиагональная матрица имеет вид
| * | * | 0 | |||
| * | * | * | |||
| * | * | * | |||
| . | . | . | . | . | . |
| * | * | * | |||
| 0 | * | * | * | ||
| * | * |
Важность трехдиагональной формы обусловлена тем, что некоторые методы преобразований подобия позволяют привести произвольную матрицу к этому частному виду.
3. Матрица A называется ортогональной, если
где Ат—транспонированная матрица A, а Е—единичная матрица. Очевидно, матрица, обратная ортогональной, эквивалентна транспонированной.
4. Матрицы А и В называются подобными, если существует такая несингулярная матрица Р, что справедливо соотношение
Основные свойства собственных значений.
1. Все п собственных значений симметричной матрицы размерности пХп, состоящей из действительных чисел, действительные. Это полезно помнить, так как матрицы, встречающиеся в инженерных расчетах, часто бывают симметричными.
2. Если собственные значения матрицы различны, то ее собственные векторы ортогональны. Совокупность п линейно независимых собственных векторов образует базис рассматриваемого пространства. Следовательно, для совокупности линейно независимых собственных векторов
Xi, где i == 1,. . ., n,
любой произвольный вектор в том же пространстве можно выразить через собственные векторы. Таким образом,
3. Если две матрицы подобны, то их собственные значения совпадают. Из подобия матриц A и В следует, что
Если принять Х == РY, то
Таким образом, матрицы A и В не только имеют одинаковые собственные значения, но и их собственные векторы связаны соотношением
4. Умножив собственный вектор матрицы на скаляр, получим собственный вектор той же матрицы. Обычно все собственные векторы нормируют, разделив каждый элемент собственного вектора либо на его наибольший элемент, либо на сумму квадратов всех других элементов.
3 . ИТЕРАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ.
Пожалуй, наиболее очевидным способом решения задачи на собственные значения является их определение из системы уравнений
которая имеет ненулевое решение лишь в случае, если det(A — lE)=0. Раскрыв определитель, получим многочлен п-й степени относительно l, корни которого и будут собственными значениями матрицы. Для определения корней можно воспользоваться любым из методов, описанных в гл. 2. К сожалению, в задачах на собственные значения часто встречаются кратные корни. Так как итерационные методы, в этих случаях не гарантируют получение решения, то для определения собственных значений следует пользоваться другими итерационными методами.
Определение наибольшего собственного значения методом итераций
На рис. 1 показана блок-схема простейшего итерационного метода отыскания наибольшего собственного значения системы
Процедура начинается с пробного нормированного вектора X(0). Этот вектор умножается слева на матрицу A, и результат приравнивается произведению постоянной (собственное значение) и нормированному вектору X(0).. Если вектор X(0) совпадает с вектором X(0), то счет прекращается. В противном случае новый нормированный вектор используется в качестве исходного и вся процедура повторяется. Если процесс сходится, то постоянный множитель соответствует истинному наибольшему собственному значению, а нормированный вектор — соответствующему собственному вектору. Быстрота сходимости этого итерационного процесса зависит от того насколько удачно выбран начальный вектор. Если он близок к истинному собственному вектору, то итерации сходятся очень быстро. На быстроту сходимости влияет также и отношение величин двух наибольших собственных значений. Если это отношение близко к единице, то сходимость оказывается медленной.
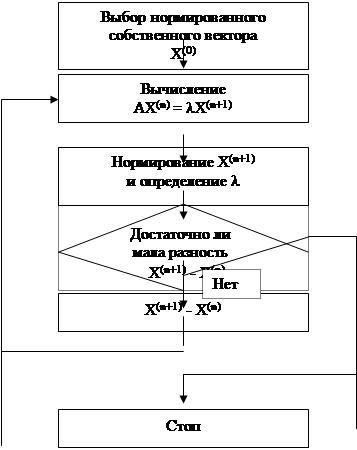 |
Рис. 1. Блок-схема алгоритма иитерационного метода решения задач на собственные значения.
Исследуем трехосное напряженное состояние элемента тела, представленного на рисунке 2. Матрица напряжений для него имеет вид
| 10 | 5 | 6 | |
| 5 | 20 | 4 | * 106 Н/м2 |
 6 6 | 4 | 30 |
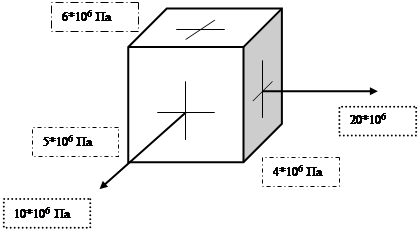 |
Рисунок 2.Трехосное напряженное состояние элемента тела.
Если исходить из того, что разрушение произойдет при максимальном напряжении, то необходимо знать величину наибольшего главного напряжения, которое соответствует наибольшему собственному значению матрицы напряжений. Для нахождения этого напряжения воспользуемся методом итерации Ниже приведена программа для ЭВМ, с помощью которой итерационная процедура осуществляется до тех пор, пока разность между собственными значениями, вычисленными в последовательных итерациях, не станет менее 0,01%. В программе использованы две подпрограммы — GMPRD из пакета программ для научных исследований фирмы IВМ, служащая для перемножения матриц и NORML, нормирующая собственные векторы по наибольшему элементу.
Программа определения собственных значений Программа позволяет определить наибольшее главное напряжение (собственное значение) для данного трехосного напряженного состояния. Применяется метод итераций. Счет прекращается, когда изменение собственного значения становится менее 0,01 процента или число итераций превышает 50.
WRITE(6 104) I,X(1),X(2),X(3)
CALL GMPRD (S, X, R, 3, 3, 1)
IF(ABS((XOLD-XLAM)/XLAM).LE.0.0001) GO TO 3
100 FORMAT (1X 54C’-»))
FORMAT (2X ‘ITERATION’, ЗХ ‘ITERATION’, 11X,‘EIGENVECTOR’)
FORMAT (3X ‘NUMBER», 6X ,'(N/M**2)’, 5X, ‘X(1)’,
103 FORMAT (1X,I5,7X,E12.5,3F10.5)
104 FORMAT (1X,I5,19X,3F10.5)
Эта подпрограмма находит наибольший из трех элементов собственного вектора и нормирует собственный вектор по этому наибольшему элементу.
# FIND THE LARGEST ELEMENT
# Нормирование по XBIG
Результат работы программы получаем в виде:
Отметим, что для достижения требуемой точности потребовалось 14 итераций.
Определение наименьшего собственного значения методом итераций
В некоторых случаях целесообразно искать наименьшее, а не наибольшее собственное значение. Это можно сделать, предварительно умножив исходную систему на матрицу, обратную A:
Если обе части этого соотношения умножим на 1/l, то получим
Ясно, что это уже иная задача на собственное значение, для которой оно равно 1/l, а рассматриваемой матрицей является A-1. Максимум 1/l, достигается при наименьшем l. Таким образом, описанная выше итерационная процедура может быть использована для определения наименьшего собственного значения новой системы.
Определение промежуточных собственных значений методом итераций
Найдя наибольшее собственное значение, можно определить следующее за ним по величине, заменив исходную матрицу матрицей, содержащей лишь оставшиеся собственные значения. Используем для этого метод, называемый методом исчерпывания. Для исходной симметричной матрицы A с известным наибольшим собственным значением l1 и собственным вектором X1 можно воспользоваться принципом ортогональности собственных векторов, т. е. записать
ХiT Хj =0 при ij и ХiT Хj =1 при i=j.
Если образовать новую матрицу A* в соответствии с формулой
то ее собственные значения и собственные векторы будут связаны соотношением
Из приведенного выше выражения для матрицы A* следует, что
A* Хi = AХi -lХ1 Х1TXi.
Здесь при i = 1 свойство ортогональности позволяет привести правую часть к виду
Но по определению собственных значений матрицы A это выражение должно равняться нулю. Следовательно, собственное значение l1 матрицы A* равно нулю, а все другие ее собственные значения совпадают с собственными значениями матрицы A. Таким образом, матрица A* имеет собственные значения 0, l2, l3,. . ., ln и соответствующие собственные векторы Х1, Х2, Хз,. . . . Хn. В результате выполненных преобразований наибольшее собственное значение l1 было изъято, и теперь, чтобы найти следующее наибольшее собственное значение l2, можно применить к матрице A* обычный итерационный метод. Определив l2 и Х2, повторим весь процесс, используя новую матрицу A**, полученную с помощью A*, l2 и Х2. Хотя на первый взгляд кажется, что этот процесс должен быстро привести к цели, он имеет существенные недостатки. При выполнении каждого шага погрешности в определении собственных векторов будут сказываться на точности определения следующего собственного вектора и вызывать накопление ошибок. Поэтому описанный метод вряд ли применим для нахождения более чем трех собственных значений, начиная с наибольшего или наименьшего. Если требуется получить большее число собственных значений, следует пользоваться методами преобразования подобия.
4. ОПРЕДЕЛЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ МЕТОДАМИ ПРЕОБРАЗОВАНИЙ ПОДОБИЯ
Метод преобразований подобия применяется с целью получить из исходной матрицы новую с теми же собственными значениями, но более простого вида. Очевидно, самым лучшим упрощением было бы приведение матрицы к чисто диагональному виду, так как в этом случае собственные значения просто соответствовали бы элементам матрицы, стоящим на главной диагонали. К сожалению, большая часть методов преобразования не позволяет этого сделать, и приходится довольствоваться приведением матрицы к трехдиагональной форме.
Метод Якоби позволяет привести матрицу к диагональному виду, последовательно, исключая все элементы, стоящие вне главной диагонали. К сожалению, приведение к строго диагональному виду требует бесконечно большого числа шагов, так как образование нового нулевого элемента на месте одного из элементов матрицы часто ведет к появлению ненулевого элемента там, где ранее был нуль. На практике метод Якоби рассматривают, как итерационную процедуру, которая в принципе позволяет достаточно близко подойти к диагональной форме, чтобы это преобразование можно было считать законченным. В случае симметричной матрицы A действительных чисел преобразование выполняется с помощью ортогональных матриц, полученных в результате вращении в действительной плоскости. Вычисления осуществляются следующим образом. Из исходной матрицы А образуют матрицу A1 == Р1АР1T. При этом ортогональная матрица Р1 выбирается так, чтобы в матрице А1 появился нулевой элемент, стоящий вне главной диагонали. Затем из А1 с помощью второй преобразующей матрицы Р2, образуют новую матрицу A2. При этом Р2, выбирают так, чтобы в A2 появился еще один нулевой внедиагональный элемент. Эту процедуру продолжают, стремясь, чтобы на каждом шаге в нуль обращался наибольший внедиагональный элемент. Преобразующая матрица для осуществления указанной операции на каждом шаге конструируется следующим образом. Если элемент аkl матрицы Ат-1 имеет максимальную величину, то Рт соответствует
Pkk = Pll = cos q,
Pkl = — Plk = sin q,
Pii = 1 при i k, l, Pij = 0 при i j.
Матрица Ат будет отличаться от матрицы Am-1 только строками и столбцами с номерами k и l. Чтобы элемент аkl(m) был равен нулю, значение q выбирается так, чтобы
| k | l | |||||||
| 1 | ||||||||
| 1 | ||||||||
| 1 | ||||||||
| 1 | ||||||||
| 1 | ||||||||
| Cos q | . | . | . | . | . | . | sin q | k |
| 1 | ||||||||
| 1 | ||||||||
| Pm = | 1 | |||||||
| 1 | ||||||||
| 1 | ||||||||
| 1 | ||||||||
| — sin q | Cos q | l | ||||||
| 1 | ||||||||
| 1 | ||||||||
| 1 | ||||||||
| 1 |
Значения q заключены в интервале
— — 0, число собственных значений матрицы A, больших b, равно числу изменений знака последовательности
1, f1 (b), f2 (b), … , (1)n fn (b).
Если целое число, равное числу изменений знака, обозначить через V(b), то число собственных значений в интервале действительных чисел [b, с] будет равно V(b)—V(c).
💥 Видео
Собственные значения и собственные векторы. ПримерСкачать

Квантовая механика 8 - Операторы. Собственные векторы и собственные значения.Скачать

Собственные векторы и собственные числа линейного оператораСкачать

Собственные значения матрицыСкачать

Овчинников А. В. - Линейная алгебра - Собственные значения и собственные векторы линейного оператораСкачать

Айгенвектора и айгензначения | Сущность Линейной Алгебры, глава 10Скачать

2.2 Итерационные методы решения СЛАУ (Якоби, Зейделя, релаксации)Скачать

Собственные числа матрицыСкачать

Вычислительные методы алгебры - Степенной метод, метод вращенийСкачать

Собственные векторы и собственные числа линейного оператора | 21 | Константин Правдин | ИТМОСкачать



