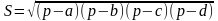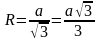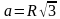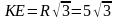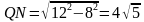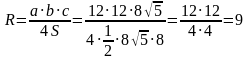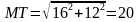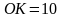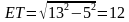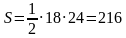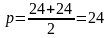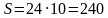Треугольник вписанный в окружность km 12 kt 16 ko

Видео:15 задание треугольники огэ по математике / маттаймСкачать

Ваш ответ

Видео:Задание 16 (В1) ОГЭ по математике ▶ №11 (Минутка ОГЭ)Скачать

решение вопроса

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Похожие вопросы

• Все категории
• экономические 43,282
• гуманитарные 33,619
• юридические 17,900
• школьный раздел 607,061
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:Расстояние между центрами вписанной и описанной окружностей треугольника и их радиусами #ShortsСкачать

Подготовка к контрольной работе

Урок №8. СКАЧИВАЙТЕ файл на устройства, чтобы все знаки и формулы были видны и распознаны. Во время чтения файла онлайн происходит потеря формул.

Просмотр содержимого документа
«Подготовка к контрольной работе»

Тема: Подготовка к контрольной работе

Задачи: обобщить и систематизировать теоретически знания и умения решать задачи по теме.

Если около четырехугольника можно описать окружность, то его площадь равна

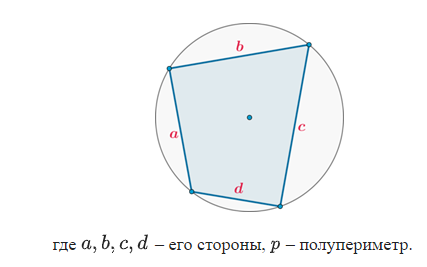
Если в четырехугольник можно вписать окружность, то его площадь равна

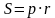
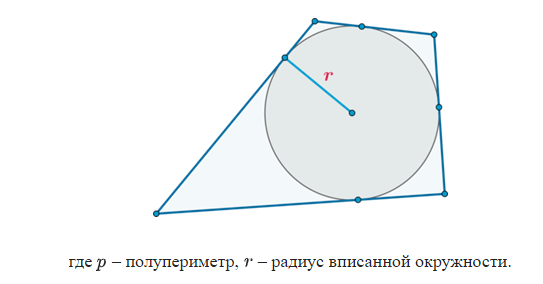
Задача 1. Равносторонний треугольник KME вписан в окружность радиуса 5. Найти сторону треугольника.

Решение (краткое). Воспользуемся формулой для радиуса описанной окружности около равностороннего треугольника:

Преобразуем её в формулу для нахождения стороны:

Тогда сторона треугольника:

Ответ: .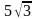

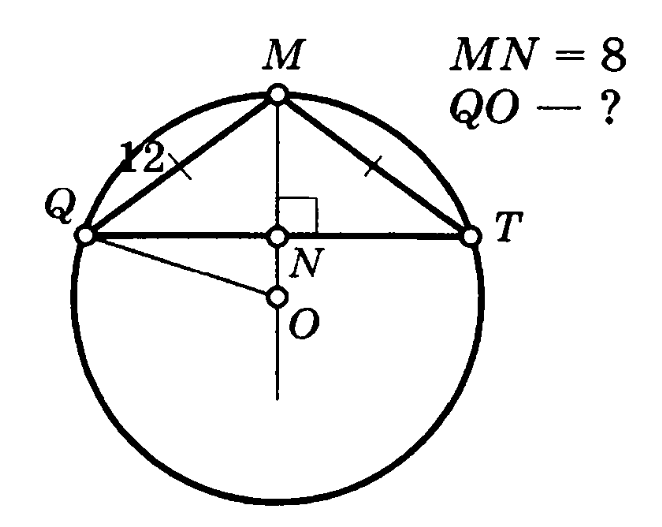
Задача 2. Равнобедренный треугольник QMT вписан в окружность. Высота треугольника MN=8, боковая сторона QM=MT=12. Найти радиус окружности.

Решение (краткое). Найдем QN из треугольника QMN:

Тогда сторона QT= .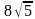

Применим формулу для нахождения радиуса описанной окружности:

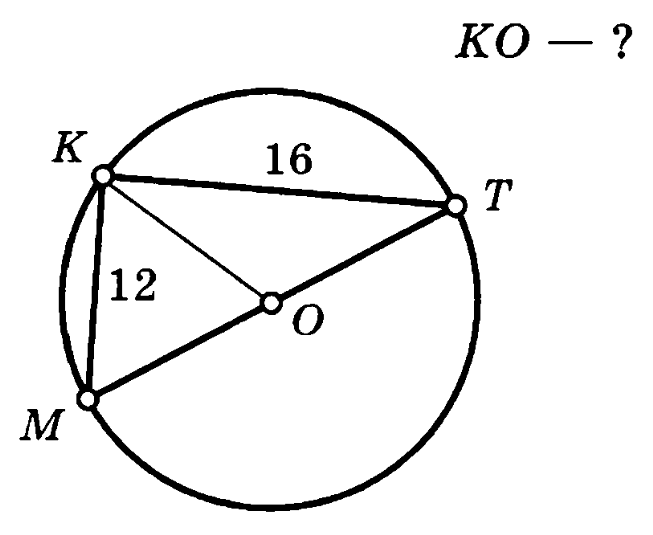
Задача 3. Треугольник MKT вписан в окружность, угол MKT опирается на диаметр. Стороны треугольника KM=12, KT=16. Найти радиус окружности.

Решение (краткое). Найдем длину стороны MT:

Т.к. MT – это диаметр окружности, то радиус вдвое меньше.

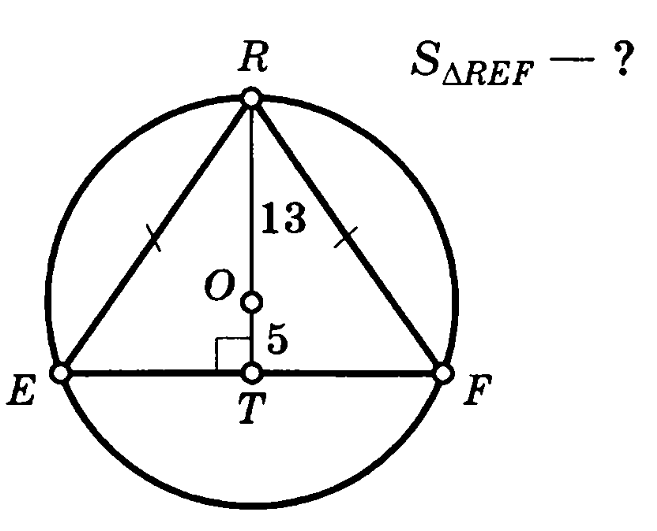
Задача 4. Равнобедренный треугольник REF вписан в окружность. Центр окружности делит высоту треугольника RS на отрезки RO=13 и OT=5. Найти площадь треугольника REF.

Решение (краткое). RO=OE=OF=13. Найдем ET:

Тогда сторона EF=2ET=24.

Найдем площадь треугольника:

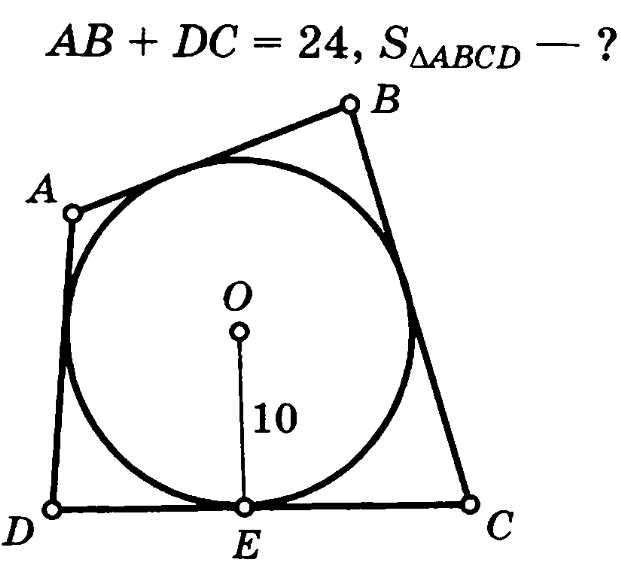
Задача 5. В четырехугольник ABCD вписана окружность радиуса 10. Сумма противоположных сторон четырехугольника равна 24. Найти площадь четырехугольника.

Решение (краткое). Найдем площадь четырехугольника по формуле .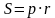

По свойству AB+DC=AD+BC=24, тогда полупериметр равен:

Тогда

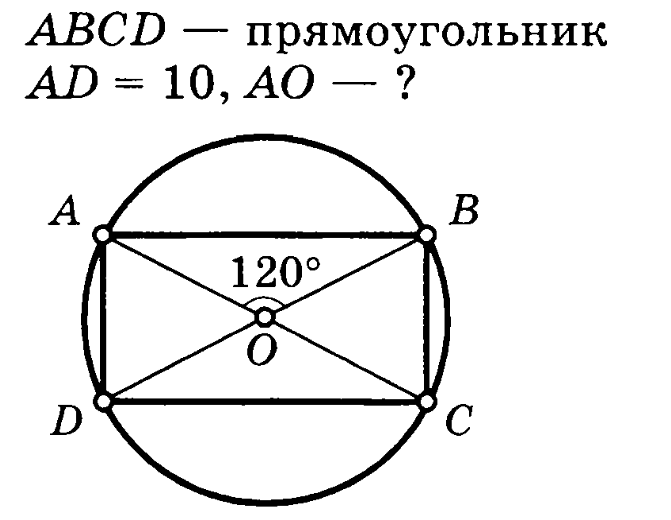
Задача 6. Прямоугольник ABCD вписан в окружность. Меньшая из его сторон равна 10, а тупой угол между диагоналями равен 120°. Найти радиус окружности.

Решение (краткое). Угол AOD=60°, AO=DO, следовательно, треугольник AOD равносторонний. AO=10.

ПОДВЕДЕНИЕ ИТОГОВ УРОКА. РЕФЛЕКСИЯ

Домашнее задание: подготовиться к контрольной работе, вспомнить теорию и решения задач.

Видео:Задание 16 ОГЭ по математике. Окружность вписана в равносторонний треугольник.Скачать

Треугольник вписанный в окружность

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Определение

Треугольник, вписанный в окружность — это треугольник, который
находится внутри окружности и соприкасается с ней всеми тремя вершинами.

На рисунке 1 изображена окружность, описанная около
треугольника и окружность, вписанная в треугольник.

ВD = FC = AE — диаметры описанной около треугольника окружности.

O — центр вписанной в треугольник окружности.

Видео:ОГЭ 2019. Задание 17. Разбор задач. Геометрия. Окружность.Скачать

Формулы

Радиус вписанной окружности в треугольник

r — радиус вписанной окружности.

1. Радиус вписанной окружности в треугольник,
   если известна площадь и все стороны:

Радиус вписанной окружности в треугольник,
если известны площадь и периметр:

Радиус вписанной окружности в треугольник,
если известны полупериметр и все стороны:

Радиус описанной окружности около треугольника

R — радиус описанной окружности.

1. Радиус описанной окружности около треугольника,
   если известна одна из сторон и синус противолежащего стороне угла:

Радиус описанной окружности около треугольника,
если известны все стороны и площадь:

Радиус описанной окружности около треугольника,
если известны все стороны и полупериметр:

Площадь треугольника

S — площадь треугольника.

1. Площадь треугольника вписанного в окружность,
   если известен полупериметр и радиус вписанной окружности:

Площадь треугольника вписанного в окружность,
если известен полупериметр:

Площадь треугольника вписанного в окружность,
если известен высота и основание:

Площадь треугольника вписанного в окружность,
если известна сторона и два прилежащих к ней угла:

Площадь треугольника вписанного в окружность,
если известны две стороны и синус угла между ними:

[ S = fracab cdot sin angle C ]

Периметр треугольника

P — периметр треугольника.

1. Периметр треугольника вписанного в окружность,
   если известны все стороны:
   

Периметр треугольника вписанного в окружность,
если известна площадь и радиус вписанной окружности:

Периметр треугольника вписанного в окружность,
если известны две стороны и угол между ними:

Сторона треугольника

a — сторона треугольника.

1. Сторона треугольника вписанного в окружность,
   если известны две стороны и косинус угла между ними:

Сторона треугольника вписанного в
окружность, если известна сторона и два угла:

Средняя линия треугольника

l — средняя линия треугольника.

1. Средняя линия треугольника вписанного
   в окружность, если известно основание:
   

Средняя линия треугольника вписанного в окружность,
если известныдве стороны, ни одна из них не является
основанием, и косинус угламежду ними:

Высота треугольника

h — высота треугольника.

1. Высота треугольника вписанного в окружность,
   если известна площадь и основание:

Высота треугольника вписанного в окружность,
если известен сторона и синус угла прилежащего
к этой стороне, и находящегося напротив высоты:

[ h = b cdot sin alpha ]

Высота треугольника вписанного в окружность,
если известен радиус описанной окружности и
две стороны, ни одна из которых не является основанием:

Видео:Треугольник. Расстояние от вершины до точки касания вневписанной окружности. Задание 16Скачать

Свойства

• Центр вписанной в треугольник окружности
  находится на пересечении биссектрис.
• В треугольник, вписанный в окружность,
  можно вписать окружность, причем только одну.
• Для треугольника, вписанного в окружность,
  справедлива Теорема Синусов, Теорема Косинусов
  и Теорема Пифагора.
• Центр описанной около треугольника окружности
  находится на пересечении серединных перпендикуляров.
• Все вершины треугольника, вписанного
  в окружность, лежат на окружности.
• Сумма всех углов треугольника — 180 градусов.
• Площадь треугольника вокруг которого описана окружность, и
  треугольника, в который вписана окружность, можно найти по
  формуле Герона.

Видео:РАДИУС вписанной окружности #математика #огэ #огэматематика #данирСкачать

Доказательство

Около любого треугольника, можно
описать окружность притом только одну.

окружность и треугольник,
которые изображены на рисунке 2.

окружность описана
около треугольника.

1. Проведем серединные
   перпендикуляры — HO, FO, EO.
2. O — точка пересечения серединных
   перпендикуляров равноудалена от
   всех вершин треугольника.
3. Центр окружности — точка пересечения
   серединных перпендикуляров — около
   треугольника описана окружность — O,
   от центра окружности к вершинам можно
   провести равные отрезки — радиусы — OB, OA, OC.

окружность описана около треугольника,
что и требовалось доказать.

Подводя итог, можно сказать, что треугольник,
вписанный в окружность — это треугольник,
в котором все серединные перпендикуляры
пересекаются в одной точке, и эта точка
равноудалена от всех вершин треугольника.

🎥 Видео

Треугольник и окружность #shortsСкачать

Деление окружности на 3; 6; 12 равных частейСкачать

ОГЭ ЗАДАНИЕ 16 РАЗДЕЛ ГЕОМЕТРИЯ ПРАВИЛЬНЫЙ ТРЕУГОЛЬНИК И ОКРУЖНОСТЬСкачать

Окружность №16 из ОГЭ. Вписанные и описанные многоугольники. Квадрат и окружность.Скачать

Вся геометрия треугольника в одной задаче. Планиметрия. ЕГЭ 2023 математика задача 16Скачать

ОГЭ. Задача на описанную окружность № 16. Как легко решить задачуСкачать

Много окружностей. Геометрия, задание №16 12+Скачать

Урок 2. Описанная окружность около четырехугольника. Задача из ОГЭ| Подобные треугольникиСкачать

Треугольник, вписанный в окружность геометрия 7 классСкачать

Окружность || Часть 4 || Треугольник, вписанный в окружностьСкачать

Четырехугольники, вписанные в окружность. 9 класс.Скачать