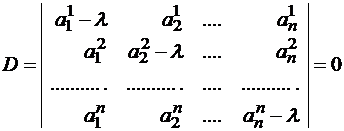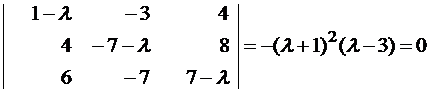Собственные векторы ортогональны если (2 видео)

Ортогональность собственных векторов.

Теорема: собственные векторы симметричного линейного оператора, соответствующие различным собственным числам, взаимно ортогональны.

Пусть векторы и — собственные векторы оператора соответствующие собственным числам λ₁ и λ₂, причем λ₁≠λ₂ . По определению симметричного оператора:

. Подставляя сюда и получим . Вынесем λ₁ и λ₂ за знак скалярного произведения, перенесем все влево и разложим на множители и получим , так как λ₁≠λ₂ , то =0, что означает взаимную ортогональность векторов и .

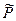
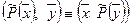
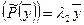
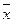
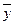
Квадратичные формы.

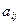
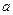
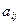
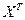
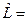
Пусть L=( )- симметричная матрица n-го порядка, тогда выражение -называется квадратичной формой переменных x₁,x₂. x_n. Матрица L=( _ij) i,j=(1,2. n) -называется матрицей квадратичной формы. Пусть( ) –симметричная матрица, т.е. = . В матричной форме квадратичная форма имеет вид :

, где X= -матрица столбец переменных, а = — матрица строка этих же переменных. Найдем произведение этих матриц.

-что является по определению квадратичной формой.

Канонический вид квадратичной формы

Следует отметить, что с помощью некоторых линейных преобразований квадратичную форму можно привести к наиболее простому каноническому виду. Квадратичная форма называется канонической, если все ее коэффициенты при i ≠ j ,т.е.

матрица канонической квадратичной формы является диагональной.

Теорема. Любая квадратичная форма с помощью линейных преобразований может быть приведена к каноническому виду.

Канонический вид квадратичной формы не является однозначно определенным, так как одна и та же квадратичная форма может быть приведена к каноническому виду многими способами. Однако полученные различными способами канонические формы обладают рядом общих свойств. Одно из них — закон инерции квадратичных форм формулируется в виде теоремы.

Теорема (закон инерции квадратичных форм). Число слагаемых с положительными (отрицательными) коэффициентами квадратичной формы не зависит от способа приведения формы к этому виду.

IV Аналитическая геометрия на плоскости.

Система координат. Основные понятия.

Под системой координат на плоскости понимают способ, позволяющий численно описать положение точки плоскости. Одной из таких систем является прямоугольная (декартова) система координат. Она задается двумя взаимно перпендикулярными прямыми — осями, на каждой из которых выбрано направление и задан масштабный единичный отрезок. Единицу масштаба обычно берут одинаковую для обеих осей. Эти оси называются осями координат, а точка их пересечения – О- началом координат. Одна ось- ось абсцисс (Оx), вторая- ординат (Оy).

На рисунках ось абсцисс, как правило, располагается горизонтально и слева направо, ось ординат вертикально и снизу вверх. Единичные векторы осей обозначают i и j (|i|=|j|=1,i перпенд. j ).

Рассмотрим произвольную точку М на плоскости Оxy. Вектор называется радиусом вектора. Координатами точки М называются координаты радиуса вектора ОМ. Если ОМ= (x ,y), то координаты т.М(x,y). Другой важной системой координат является полярная система координат.

Полярная система координат задается точкой О называемой полюсом, лучом Оp называемом полярной осью и единичным вектором 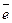того же направления, что и луч Оp.

Возьмем точку М не совпадающую с О. Положение т.М определяется двумя числами ее расстоянием rот полюса О и углом образованным отрезком ОМ с полярной осью (отсчет углов ведется в направлении противоположном движению часовой стрелки. Числа r и φ называются полярными координатами т.М (r, ), r – полярный радиус, — полярный угол.

Установим связь между декартовыми и полярными координатами. Для этого совместим полюс с системой координат Оxy, а полярную ось с + полуосью Ox. Тогда т.М в прямоугольной системе М( x,y),а в полярном M(r,φ).тогда из рисунка 1

y M(x,y)

или y

Рис.1

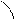
O Xx

1) Линия на плоскости(основные понятия)

Уравнение линии(кривой) на плоскости Oxy называют такое уравнение F(x,y)=0 с двумя переменными, которому удовлетворяют координаты x и y каждой точки линии и не удовлетворяют координаты любой точки не лежащей на этой линии. Если точка M(x,y) передвигается по линии, то ее координаты изменяясь, удовлетворяют уравнению этой линии.

Пример: лежат ли точки А(-2,1) и В(1,1) на линии 2x+y+3=0.

Решение. Подставляя в уравнение вместо x и y координаты точек А и В получим в первом тождество во втором нет. Следовательно т. А лежит на линии, т.В- нет.

Уравнение линии на плоскости можно задать при помощи двух уравнений:

Где x и y- координаты т.М(x,y),лежащей на данной линии, а t-переменная называемая параметром. Параметр t определяет положение точки (x,y) на плоскости. Если параметр t меняется, то точка на плоскости перемещается, описывая данную линию. Такое уравнение называется параметрическим уравнением линии. Для перехода от параметрического вида к обычному достаточно из уравнений (1) исключить t. Каким-либо образом линию на плоскости можно задать векторным уравнением , где t – скалярный переменный параметр. Каждому t₀ соответствует определенный вектор r₀=r(t₀). При изменении параметра t конец вектора r=r(t) опишет заданную линию.

Векторное уравнение и параметрическое уравнение имеют механический смысл. Если точка перемещается на плоскости, то указанные уравнения называются уравнениями движения, а линия- траекторией движения, параметр t при этом– время.

В аналитической геометрии на плоскости, вообще говоря, возникают две задачи:

1) зная геометрические свойства кривой, найти ее уравнение

2)зная уравнение кривой изучить ее форму и свойства.

Содержание

Собственные числа и собственные векторы линейного оператора
Правило отыскания собственных чисел и собственных векторов
Основные понятия о собственных значениях матриц
🎬 Видео

Видео:Собственные векторы и собственные числа линейного оператораСкачать

Собственные числа и собственные векторы линейного оператора

Определение . Ненулевой вектор x называется собственным вектором оператора A , если оператор A переводит x в коллинеарный ему вектор, то есть A· x = λ· x . Число λ называется собственным значением или собственным числом оператора A, соответствующим собственному вектору x .
Отметим некоторые свойства собственных чисел и собственных векторов.
1. Любая линейная комбинация собственных векторов x ₁, x ₂, . x _m оператора A , отвечающих одному и тому же собственному числу λ, является собственным вектором с тем же собственным числом.
2. Собственные векторы x ₁, x ₂, . x _m оператора A с попарно различными собственными числами λ₁, λ₂, …, λ_m линейно независимы.
3. Если собственные числа λ₁=λ₂= λ_m= λ, то собственному числу λ соответствует не более m линейно независимых собственных векторов.

Итак, если имеется n линейно независимых собственных векторов x ₁, x ₂, . x _n, соответствующих различным собственным числам λ₁, λ₂, …, λ_n, то они линейно независимы, следовательно, их можно принять за базис пространства R_n. Найдем вид матрицы линейного оператора A в базисе из его собственных векторов, для чего подействуем оператором A на базисные векторы: 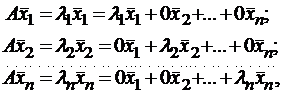тогда .
Таким образом, матрица линейного оператора A в базисе из его собственных векторов имеет диагональный вид, причем по диагонали стоят собственные числа оператора A.
Существует ли другой базис, в котором матрица имеет диагональный вид? Ответ на поставленный вопрос дает следующая теорема.

Теорема. Матрица линейного оператора A в базисе < ε _i> (i = 1..n) имеет диагональный вид тогда и только тогда, когда все векторы базиса — собственные векторы оператора A.

Видео:Собственные значения и собственные векторы матрицы (4)Скачать

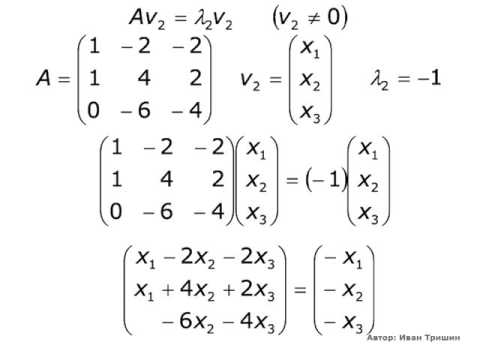
Правило отыскания собственных чисел и собственных векторов

Система (1) имеет ненулевое решение, если ее определитель D равен нулю

Пример №1 . Линейный оператор A действует в R₃ по закону A· x =(x₁-3x₂+4x₃, 4x₁-7x₂+8x₃, 6x₁-7x₂+7x₃), где x₁, x₂, . x_n — координаты вектора x в базисе e ₁=(1,0,0), e ₂=(0,1,0), e ₃=(0,0,1). Найти собственные числа и собственные векторы этого оператора.
Решение. Строим матрицу этого оператора:
A· e ₁=(1,4,6)
A· e ₂=(-3,-7,-7)
A· e ₃=(4,8,7)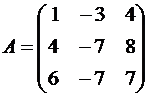
.
Составляем систему для определения координат собственных векторов:
(1-λ)x₁-3x₂+4x₃=0
x₁-(7+λ)x₂+8x₃=0
x₁-7x₂+(7-λ)x₃=0
Составляем характеристическое уравнение и решаем его:

Пример №2 . Дана матрица .
1. Доказать, что вектор x =(1,8,-1) является собственным вектором матрицы A. Найти собственное число, соответствующее этому собственному вектору.
2. Найти базис, в котором матрица A имеет диагональный вид.

Решение находим с помощью калькулятора.
1. Если A· x =λ· x , то x — собственный вектор

Определение . Симметрической матрицей называется квадратная матрица, в которой элементы, симметричные относительно главной диагонали, равны, то есть в которой a_i k =a_k i .

Замечания .

Все собственные числа симметрической матрицы вещественны.
Собственные векторы симметрической матрицы, соответствующие попарно различным собственным числам, ортогональны.

В качестве одного из многочисленных приложений изученного аппарата, рассмотрим задачу об определении вида кривой второго порядка.

Видео:2 42 Ортогональность векторовСкачать

Основные понятия о собственных значениях матриц

Большое число научно-технических задач, а также некоторые исследования в области вычислительной математики требуют нахождения собственных значений и собственных векторов матриц. Введем некоторые определения, необходимые для изложения материала данного раздела.

Рассмотрим, квадратную матрицу n-го порядка

(3.1)

Вектор x = <x1, x2,…,xn> называется собственным векторомматрицы А, соответствующим собственному значениюλ, если он удовлетворяет системе уравнений

Поскольку при умножении собственного вектора на скаляр он остается собственным вектором той же матрицы, его можно нормировать. В частности, каждую координату собственного вектора можно разделить на максимальную из них или на длину вектора; в последнем случае получится единичный собственный вектор.

Характеристической матрицейСданной матрицы Аназывается матрица вида

(3.3)

где Е — единичная матрица. Легко видеть, что систему (3.2) можно записать в виде

Если перейти к координатной форме записи вектора х, то с учетом (3.1) систему (3.4) можно записать в виде

(3.5)

Система (3.4) или (3.5) является однородной системой п линейных уравнений с п неизвестными. Она имеет ненулевые решения лишь тогда, когда ее определитель равен нулю: det C=0, причем решение не единственно.

Определитель характеристическойматрицы С является характеристический многочлен n-й степени относительно λ:

(3.6)

Корни этого многочлена являются собственными значениями матрицы А.

Для нахождения собственных векторов матрицы требуется решить систему линейных алгебраических уравнений, решение которой не единственно. Из линейной алгебры известно, что в этом случае структура общего решения системы имеет следующий вид: одно или несколько неизвестных, называемых свободными, могут принимать любые значения, а остальные неизвестные выражаются через свободные. Число свободных неизвестных равно числу уравнений системы, являющихся следствием остальных уравнений. На практике, если свободное неизвестное одно (что часто и бывает), его полагают равным некоторому числу, например единице. После этого остальные неизвестные (компоненты вектора) находят однозначно из подсистемы линейно независимых уравнений, в которой отброшено уравнение, являющееся следствием остальных. Эта процедура не влияет на результат решения задачи, поскольку, как уже отмечалось, собственные векторы находят с точностью до постоянного множителя.

Пример. Вычислить собственные числа и собственные векторы матрицы

Решение. Составим характеристический многочлен

Найдем корни этого многочлена второй степени:

Чтобы найти собственные векторы x1, х2, соответствующие собственным значениям λ1, λ2, составим системы уравнений типа (3.4), (3.5) для каждого из них.

При λ1 = 2 получим

или в координатной форме

Замечаем, что уравнения линейно зависимы. Поэтому оставляем лишь одно из них.

Из первого уравнения следует, что х2 = -х1.Неизвестное х1можно считать свободным, полагаем х1= 1. Тогда х2 = -1, и собственный вектор, соответствующий собственному значению λ1=2, имеет вид x1 = или x1= e1– е2, где е1, е2 – единичные орты выбранной базисной системы.

Аналогично находим второй собственный вектор, соответствующий собственному значению λ2 = 5. Опуская комментарии, получаем

Вектор x1 нормирован; нормируем также вектор х2, разделив его компоненты на наибольшую из них. Получим х2 = 0.5e1 + e2. Можно также привести векторы к единичной длине, разделив их компоненты на значения модулей векторов. В этом случае

Мы рассмотрели простейший пример вычисления собственных значений и собственных векторов для матрицы второго порядка. Нетрудно также провести подобное решение задачи для матрицы третьего порядка и для некоторых весьма специальных случаев.

В общем случае, особенно для матриц высокого порядка, задача о нахождении их собственных значений и собственных векторов, называемая полной проблемой собственных значений, значительно более сложная.

На первый взгляд может показаться, что вопрос сводится к вычислению корней многочлена (3.6). Однако здесь задача осложнена тем, что среди собственных значений часто встречаются кратные. И, кроме того, для произвольной матрицы непросто вычислить сами коэффициенты характеристического многочлена.

Отметим некоторые свойства собственных значений для частных типов исходной матрицы.

1. Все собственные значения симметрической матрицы действительны.

2. Если собственные значения матрицы действительны и различны, то соответствующие им собственные векторы ортогональны и образуют базис рассматриваемого пространства. Следовательно, любой вектор в данном пространстве можно выразить через совокупность линейно независимых собственных векторов.

3. Если две матрицы А и В подобны, т.е. они связаны соотношением

(3.7)

то их собственные значения совпадают (здесь Р – некоторая матрица). Преобразованиеподобия (3.7) можно использовать для упрощения исходной матрицы, а задачу о вычислении ее собственных значений свести к аналогичной задаче для более простой матрицы. Очевидно, самым лучшим упрощением матрицы (3.1) было бы приведение ее к треугольному виду

Тогда матрица (3.3) также имела бы треугольный вид. Как известно, определитель треугольной матрицы равен произведению ее диагональных элементов, поэтому характеристический многочлен (3.6) в этом случае имеет вид

Собственные значения матрицы, равные корням этого многочлена, можно получить сразу:

Таким образом, собственные значения треугольной матрицы равны ее диагональным элементам. То же самое, естественно, относится и к диагональной матрице, которая является частным случаем треугольной.

Некоторые типы матриц удается привести к треугольному виду с помощью преобразования подобия. В частности, симметрическую матрицу можно привести к диагональному виду. На практике часто используется приведение симметрической матрицы к трехдиагональному виду. Процедура вычисления собственных значений для полученной матрицы значительно упрощается по сравнению с задачей для исходной матрицы.

Существует ряд методов, основанных на использовании преобразования подобия, позволяющего привести исходную матрицу к более простой структуре. Мы рассмотрим ниже один из них – метод вращений.