Отрезок соединяющий центр верхнего основания с точкой окружности 8

Геометрия | 10 — 11 классы

Отрезок, соединяющий центр верхнего основания цилиндра с точкой на окружности нижнего основания, равен 8 см и наклонен к плоскости нижнего основания под углом 60°.

Найдите полную поверхность цилиндра.

На рисунке осевое сечение цилиндра.

Sполн = Sбок + 2Sосн

H = OO₁ = 8·sin60° = 8√3 / 2 = 4√3

R = OA = 8·cos60° = 8 / 2 = 4

Sполн = 2π·4·4√3 + 2·π·4² = 32π√3 + 32π = 32π(√3 + 1).

) = πR² h, где R — радиус основания, h — высота цилиндра.

Рассмотрим прямоугольный треугольник, в котором отрезок, соединяющий центр верхнего основания с точкой окружности нижнего основания, — это гипотенуза, а высота и радиус основания цилиндра — это катеты.

R = sin60 * 8 = √3 / 2 * 8 = 4√3

По теореме Пифагора :

V = 16 * 3 * 4 * π = 192π

Видео:Геометрия 11 класс (Урок№8 - Сфера и шар.)Скачать

Цилиндр, радиус основания которого равен 10, пересечен плоскостью, параллельной его оси?

Цилиндр, радиус основания которого равен 10, пересечен плоскостью, параллельной его оси.

Дуга окружности основания, отсекаемая плоскостью сечения равна 120o.

Диагональ сечения наклонена к плоскости основания цилиндра под углом 80o.

Найдите расстояние от оси цилиндра до плоскости сечения.

Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Радиус основания цилиндра равен 12?

Радиус основания цилиндра равен 12.

Найдите диагональ осевого сечения цилиндра если она наклонена к плоскости основания цилиндра под углом 45 градусов.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Помогите пожалуйста с геометрией?

Помогите пожалуйста с геометрией.

Вершины квадрата принадлежат окружностям верхнего и нижнего оснований цилиндра.

Найдите площадь поверхности цилиндра, если радиус основания цилиндра равен 7 см, сторона квадрата — 10 см и плоскость квадрата пересекает ось цилиндра.

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

В цилиндре параллельно его оси проведена плоскость, пересекающая нижнюю основу цилиндра по хорде, которая видна из центра этой основе под углом α?

В цилиндре параллельно его оси проведена плоскость, пересекающая нижнюю основу цилиндра по хорде, которая видна из центра этой основе под углом α.

Диагональ образованного сечения наклонена к плоскости основания под углом β Найдите площадь боковой поверхности и объем цилиндра, если площадь его основания равна S.

Видео:🔴 В окружности с центром O отрезки AC и BD ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 15 | ШКОЛА ПИФАГОРАСкачать

Диагональ осевого сечения цилиндра равен 2 см и наклонена к плоскости основаня под углом 60° ?

Диагональ осевого сечения цилиндра равен 2 см и наклонена к плоскости основаня под углом 60° .

Найдите объем цилиндра.

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

99 баллов?

Дал бы больше но нельзя.

Боковая поверхность правильной треугольной призмы 6 .

Найдите высоту призмы , если прямая, проходящая через центр верхнего основания и середину стороны нижнего основания , наклонена к плоскости основания под углом 60°.

Видео:Длина окружности. Площадь круга. 6 класс.Скачать

Диаметр основания цилиндра равен 2 см, высота равна длине окружности основания вычислите боковую и полную поверхности цилиндра?

Диаметр основания цилиндра равен 2 см, высота равна длине окружности основания вычислите боковую и полную поверхности цилиндра.

Видео:Урок по теме ЦЕНТРАЛЬНЫЕ И ВПИСАННЫЕ УГЛЫ 8 КЛАСССкачать

Отрезок соеденяющий центр верхнего основания целиндра с серединой радиуса нижнего основания, равен 12см и образует с осью цилиндра угол 30°?

Отрезок соеденяющий центр верхнего основания целиндра с серединой радиуса нижнего основания, равен 12см и образует с осью цилиндра угол 30°.

Найдите площадь осевого сечения цилиндра.

ПОЖАЛУЙСТА, НАПИШИТЕ ПРАВИЛЬНОЕ РЕШЕНИЕ БЕЗ ПОЯСНЕНИЙ.

Видео:ОГЭ 2023. РАЗБОР ЗАДАНИЯ №16 "Окружность"Скачать

Диагональ осевого сечения цилиндра наклонена к плоскости основания под углом 30º?

Диагональ осевого сечения цилиндра наклонена к плоскости основания под углом 30º.

Площадь основания равна 36π см².

Найдите площадь полной поверхности цилиндра.

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Квадрат ABCD и цилиндр расположены таким образом, что AB диаметр верхнего основания цилиндра а CD лежит в плоскости нижнего основания и касается его окружности?

Квадрат ABCD и цилиндр расположены таким образом, что AB диаметр верхнего основания цилиндра а CD лежит в плоскости нижнего основания и касается его окружности.

А) Докажите, что плоскость квадрата наклонена к плоскости основания цилиндра под углом 60

б)Найдите длину той части отрезка BD которая находится внутри цилиндра если образующая равна корень из 6.

На этой странице сайта, в категории Геометрия размещен ответ на вопрос Отрезок, соединяющий центр верхнего основания цилиндра с точкой на окружности нижнего основания, равен 8 см и наклонен к плоскости нижнего основания под углом 60°?. По уровню сложности вопрос рассчитан на учащихся 10 — 11 классов. Чтобы получить дополнительную информацию по интересующей теме, воспользуйтесь автоматическим поиском в этой же категории, чтобы ознакомиться с ответами на похожие вопросы. В верхней части страницы расположена кнопка, с помощью которой можно сформулировать новый вопрос, который наиболее полно отвечает критериям поиска. Удобный интерфейс позволяет обсудить интересующую тему с посетителями в комментариях.

ABCD — трапеция (буквы можешь расположить, как хочешь)AC — диагональBC = 10L ACB = L DL CAD = L ACB (по свойству трапеции) — — — — — — > L D = L CAD — — — — — > AC = CDL ACB = L CAD — — — — — > L BAD = 90 град. — — — — > L D = L CAD = L ACB = 90 2..

M(x1 ; y1) n(x2 ; y2) середина = ((x2 — x1) / 2 ; (y2 — y1) / 2) 1) (5 ; 2) 2)(1 ; 3) 3)(1, 5 ; 4, 5).

S = 6 * 10 * 8 * 20 = 9600 Вот.

Всё 12 ребер у куба равны. Найдем длину одного : 48 : 12 = 4 Все 6 граней — равные квадраты. Тогда площадь S = 6 * 4² = 6 * 16 = 96.

34×85 + 34×36 = 4114 4114 : 11 = 374.

34·85 + 34·36 = 4114 1) 34·85 = 2890 2) 34·36 = 1224 3) 2890 + 1224 = 4114 4114 : 11 = 374.

A) АМ = МВ — по условию, значит АМ = 6 : 2 = 3см, так как ∠MBN = ∠MNB = 45°, МN = BM = 3см⇒AMNK — квадрат Р квадрата = 4 * 3 = 12см b) ST — средняя линияΔEDF⇒ST = 1 / 2EF = 12 / 2 = 6см. PF = (12 — QP) / 2 = (12 — 6) / 2 = 3см. ВΔTPF∠F = ∠PTF = 45°..

Видео:№146. Отрезки АВ и CD — диаметры окружности с центром О. Найдите периметр треугольника AOD, еслиСкачать

Презентация, Разбор и решение задач по теме Цилиндр

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов

Сертификат и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Подготовка к контрольной работе Цилиндр

1.Радиус основания цилиндра равен 5 см, а его образующая — 9 см. Найдите площадь полной поверхности и объем цилиндра. Дано: R= H= Найти: Sполн; V

2.Прямоугольник, стороны которого равны 6 см и 4 см, вращается около меньшей стороны. Найдите площадь поверхности тела вращения и его объем. Дано: R= H= Найти: Sполн; V

3.Осевым сечением цилиндра является квадрат, диагональ которого равна см. Найдите площадь поверхности цилиндра и его объем. R= H= Найти: Sполн; V

3.Осевым сечением цилиндра является квадрат, диагональ которого равна см. Найдите площадь поверхности цилиндра и его объем. R= H= Найти: Sполн; V

4. Высота цилиндра на 10 см больше радиуса основания, а полная поверхность равна 144 π см2. Найти объем цилиндра. R= H= Найти: Sполн; V

4. Высота цилиндра на 10 см больше радиуса основания, а полная поверхность равна 144 π см2. Найти объем цилиндра. R= H= Найти: Sбок; V

5. Радиус основания цилиндра в 3 раза меньше высоты, а площадь полной поверхности равна 288п см2. Найти объем цилиндра. R= H= Найти: Sполн; V

5. Радиус основания цилиндра в 3 раза меньше высоты, а площадь полной поверхности равна 288п см2. Найти объем цилиндра. R= H= Найти: Sполн; V

6. Высота цилиндра на 2 см меньше его радиуса. Площадь боковой поверхности цилиндра равна 160π см . Найти объем цилиндра. R= H= Найти: Sполн; V

6. Высота цилиндра на 2 см меньше его радиуса. Площадь боковой поверхности цилиндра равна 160π см . Найти объем цилиндра. R= H= Найти: Sполн; V

7. Диагональ осевого сечения цилиндра равна дм и образует с плоскостью основания цилиндра угол 45°. Найти площадь полной поверхности и объем цилиндра. Треугольник АВ1В прямоугольный, найдем АВ и ВВ1 по синусу и косинусу 45 ̊

7. Диагональ осевого сечения цилиндра равна дм и образует с плоскостью основания цилиндра угол 45°. Найти площадь полной поверхности и объем цилиндра. Треугольник АВ1В прямоугольный, найдем АВ и ВВ1 по синусу и косинусу 45 ̊

8. Диагональ осевого сечения цилиндра равна 8 см и составляет с образующей угол 60°. Найти площадь полной поверхности и объем цилиндра. Треугольник АВ1В прямоугольный, найдем АВ и ВВ1 по синусу и косинусу 60 ̊

8. Диагональ осевого сечения цилиндра равна 8 см и составляет с образующей угол 60°. Найти площадь полной поверхности и объем цилиндра.

9. Отрезок, соединяющий центр верхнего основания цилиндра с точкой окружности нижнего основания, равен 8 см и образует угол 60° с осью цилиндра. Найти площадь полной поверхности и объем цилиндра. Треугольник АО1О прямоугольный, найдем АО и ОО1 по синусу и косинусу 60 ̊

9. Отрезок, соединяющий центр верхнего основания цилиндра с точкой окружности нижнего основания, равен 8 см и образует угол 60° с осью цилиндра. Найти площадь полной поверхности и объем цилиндра. Треугольник АО1О прямоугольный, найдем АО и ОО1 по синусу и косинусу 60 ̊

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 987 человек из 79 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 310 человек из 69 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 677 человек из 75 регионов

Ищем педагогов в команду «Инфоурок»

Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Дистанционные курсы для педагогов

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 534 342 материала в базе

Материал подходит для УМК

«Математика: алгебра и начала математического анализа, геометрия. Геометрия (базовый и углубленный уровни)», Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

Другие материалы

• 26.05.2017
• 1460
• 19

• 26.05.2017
• 234
• 0

• 26.05.2017
• 1167
• 3

• 26.05.2017
• 744
• 0

• 26.05.2017
• 559
• 1

• 26.05.2017
• 734
• 0

• 26.05.2017
• 1508
• 4

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 26.05.2017 9504
• PPTX 523 кбайт
• 160 скачиваний
• Рейтинг: 4 из 5
• Оцените материал:

Настоящий материал опубликован пользователем Сидорова Елена Николаевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 4 года и 8 месяцев
• Подписчики: 0
• Всего просмотров: 138948
• Всего материалов: 100

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:1 2 4 сопряжение окружностейСкачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Путин поручил обучать педагогов работе с девиантным поведением

Время чтения: 1 минута

Полный перевод школ на дистанционное обучение не планируется

Время чтения: 1 минута

В Госдуме предложили доплачивать учителям за работу в классах, где выявлен ковид

Время чтения: 1 минута

Школьники Ленобласти уйдут на внеплановые каникулы

Время чтения: 1 минута

Минтруд рекомендовал перевести на удаленку максимальное число сотрудников

Время чтения: 1 минута

В Тульской области ввели школьные каникулы со 2 по 11 февраля

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:ЗАДАНИЕ 8 из ЕГЭ_50Скачать

В цилиндре отрезок который соединяет центр верхнего основания цилиндра

Видео:№527. Концы отрезка АВ лежат на окружностях оснований цилиндра. Радиус цилиндра равен г,Скачать

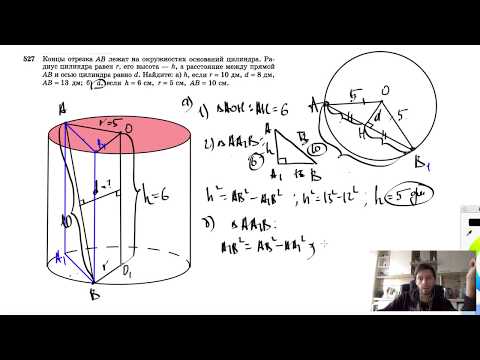
В цилиндре отрезок который соединяет центр верхнего основания цилиндра

В цилиндре отрезок, который соединяет центр верхнего основания с точкой
окружности нижнего основания, наклонен к плоскости основания под углом α.
Определить объем цилиндра, если расстояние от центра нижнего основания до
середины этого отрезка равно а.

Ответы и объяснения 1

Площадь полной поверхности цилиндра S= pi*R^2*2+2*pi*R*H, где R и H радиус и высота цилиндра.

В осевом сечении цилиндра прямоуголный треугольник с двумя катетами R и H и гипотенузой равной 2(по условию). H=1/2*2=1 как катет противолежащий углу в 30 градусов. R=√3по теореме пифагора.

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

• Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
• Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
• Писать без грамматических, орфографических и пунктуационных ошибок.

• Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
• Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
• Использовать мат — это неуважительно по отношению к пользователям;
• Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Геометрия.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.

Видео:Замечательные точки треугольника | Ботай со мной #030 | Борис Трушин ||Скачать

Отрезок, соединяющий центр верхнего основания цилиндра с точкой на окружности нижнего основания, равен 8 см и наклонен к плоскости нижнего основания под углом 60°?

Отрезок, соединяющий центр верхнего основания цилиндра с точкой на окружности нижнего основания, равен 8 см и наклонен к плоскости нижнего основания под углом 60°.

Найдите полную поверхность цилиндра.

На рисунке осевое сечение цилиндра.

Sполн = 2π·4·4√3 + 2·π·4² = 32π√3 + 32π = 32π(√3 + 1).

) = πR² h, где R — радиус основания, h — высота цилиндра.

Рассмотрим прямоугольный треугольник, в котором отрезок, соединяющий центр верхнего основания с точкой окружности нижнего основания, — это гипотенуза, а высота и радиус основания цилиндра — это катеты.

Видео:Задание 8. Часть 6. Комбинации круглых тел друг с другомСкачать

Диагональ цилиндра, равен 4 см образует с плоскостью основания угол 60°?

Диагональ цилиндра, равен 4 см образует с плоскостью основания угол 60°.

Видео:Математика 11, задача по геометрии, 2-я часть ЕГЭ, задача 16Скачать

Высота и радиус основания цилиндра соответственно равны 9 и 6, концы отрезка АВ длиной (корень из 113) лежат на окружностях верхнего и нижнего оснований?

Высота и радиус основания цилиндра соответственно равны 9 и 6, концы отрезка АВ длиной (корень из 113) лежат на окружностях верхнего и нижнего оснований.

Найдите расстояние от оси цилиндра до отрезка АВ.

Видео:№147. На окружности с центром О отмечены точки А и В так, что угол АОВ — прямой. Отрезок ВССкачать

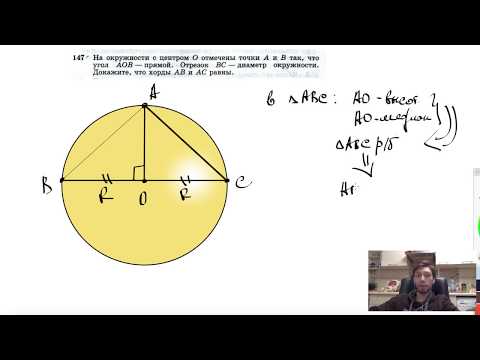
Диагональ осевого сечения цилиндра равна 12 см и наклонена к плоскости основания под углом 30 градусов вычислите площадь полного основания и Объем?

Диагональ осевого сечения цилиндра равна 12 см и наклонена к плоскости основания под углом 30 градусов вычислите площадь полного основания и Объем.

Видео:ТРАПЕЦИЯ — Что такое трапеция, Виды Трапеций, Площадь Трапеции // Геометрия 8 классСкачать

Из цилиндра выточен конус таким образом, что его основание совпадает с одним из оснований цилиндра, а вершина – с центром другого основания цилиндра?

Из цилиндра выточен конус таким образом, что его основание совпадает с одним из оснований цилиндра, а вершина – с центром другого основания цилиндра.

Найдите отношение объема сточенной части цилиндра к объему конуса.

Радиус цилиндра равен 6, а расточние от уентра одного центра основания до тоски окружности второго основания равен 10?

Радиус цилиндра равен 6, а расточние от уентра одного центра основания до тоски окружности второго основания равен 10.

Радиус основания цилиндра = 1 см, а образующая = 2 см?

Радиус основания цилиндра = 1 см, а образующая = 2 см.

Найти площадь полной поверхности цилиндра.

Радиус основания цилиндра равен 12?

Радиус основания цилиндра равен 12.

Найдите диагональ осевого сечения цилиндра если она наклонена к плоскости основания цилиндра под углом 45 градусов.

ПОМОГИТЕ ПРОШУДиагональ осевого сечения цилиндра наклонена к плоскости основания под углом 60 градусов и равна 20 см?

Диагональ осевого сечения цилиндра наклонена к плоскости основания под углом 60 градусов и равна 20 см.

Найдите площадь боковой поверхности.

Дана правильная четырёхугольная пирамида с длиной стороны a и градусной мерой угла наклона бокового ребра к плоскости основания 60°?

Дана правильная четырёхугольная пирамида с длиной стороны a и градусной мерой угла наклона бокового ребра к плоскости основания 60°.

Цилиндр помещён в данную пирамиду так, что его образующая лежит на диагонали основания, а окружности оснований цилиндра вписаны в сечения пирамиды плоскостями, содержащими эти основания.

Также известно, что высота цилиндра равна h.

Вычислите площадь полной поверхности равностороннего цилиндра диаметр основания которого равен 12 см?

Вычислите площадь полной поверхности равностороннего цилиндра диаметр основания которого равен 12 см.

Диагональ осевого сечения цилиндра равен 2 см и наклонена к плоскости основаня под углом 60° ?

Диагональ осевого сечения цилиндра равен 2 см и наклонена к плоскости основаня под углом 60° .

На этой странице сайта, в категории Геометрия размещен ответ на вопрос Отрезок, соединяющий центр верхнего основания цилиндра с точкой на окружности нижнего основания, равен 8 см и наклонен к плоскости нижнего основания под углом 60°?. По уровню сложности вопрос рассчитан на учащихся 10 — 11 классов. Чтобы получить дополнительную информацию по интересующей теме, воспользуйтесь автоматическим поиском в этой же категории, чтобы ознакомиться с ответами на похожие вопросы. В верхней части страницы расположена кнопка, с помощью которой можно сформулировать новый вопрос, который наиболее полно отвечает критериям поиска. Удобный интерфейс позволяет обсудить интересующую тему с посетителями в комментариях.

1 — 27 2 — 45 3 — 40 4 — 130 5 — 35 6 — 37 7 — 135 8 — 40 9 — 30 10 — 90.

Презентация, Разбор и решение задач по теме Цилиндр

Ищем педагогов в команду «Инфоурок»

Описание презентации по отдельным слайдам:

Подготовка к контрольной работе Цилиндр

1. Радиус основания цилиндра равен 5 см, а его образующая — 9 см. Найдите площадь полной поверхности и объем цилиндра. Дано: R= H= Найти: Sполн; V

2. Прямоугольник, стороны которого равны 6 см и 4 см, вращается около меньшей стороны. Найдите площадь поверхности тела вращения и его объем. Дано: R= H= Найти: Sполн; V

3. Осевым сечением цилиндра является квадрат, диагональ которого равна см. Найдите площадь поверхности цилиндра и его объем. R= H= Найти: Sполн; V

3. Осевым сечением цилиндра является квадрат, диагональ которого равна см. Найдите площадь поверхности цилиндра и его объем. R= H= Найти: Sполн; V

4. Высота цилиндра на 10 см больше радиуса основания, а полная поверхность равна 144 π см2. Найти объем цилиндра. R= H= Найти: Sполн; V

4. Высота цилиндра на 10 см больше радиуса основания, а полная поверхность равна 144 π см2. Найти объем цилиндра. R= H= Найти: Sбок; V

5. Радиус основания цилиндра в 3 раза меньше высоты, а площадь полной поверхности равна 288п см2. Найти объем цилиндра. R= H= Найти: Sполн; V

5. Радиус основания цилиндра в 3 раза меньше высоты, а площадь полной поверхности равна 288п см2. Найти объем цилиндра. R= H= Найти: Sполн; V

6. Высота цилиндра на 2 см меньше его радиуса. Площадь боковой поверхности цилиндра равна 160π см . Найти объем цилиндра. R= H= Найти: Sполн; V

6. Высота цилиндра на 2 см меньше его радиуса. Площадь боковой поверхности цилиндра равна 160π см . Найти объем цилиндра. R= H= Найти: Sполн; V

7. Диагональ осевого сечения цилиндра равна дм и образует с плоскостью основания цилиндра угол 45°. Найти площадь полной поверхности и объем цилиндра. Треугольник АВ1В прямоугольный, найдем АВ и ВВ1 по синусу и косинусу 45 ̊

7. Диагональ осевого сечения цилиндра равна дм и образует с плоскостью основания цилиндра угол 45°. Найти площадь полной поверхности и объем цилиндра. Треугольник АВ1В прямоугольный, найдем АВ и ВВ1 по синусу и косинусу 45 ̊

8. Диагональ осевого сечения цилиндра равна 8 см и составляет с образующей угол 60°. Найти площадь полной поверхности и объем цилиндра. Треугольник АВ1В прямоугольный, найдем АВ и ВВ1 по синусу и косинусу 60 ̊

8. Диагональ осевого сечения цилиндра равна 8 см и составляет с образующей угол 60°. Найти площадь полной поверхности и объем цилиндра.

9. Отрезок, соединяющий центр верхнего основания цилиндра с точкой окружности нижнего основания, равен 8 см и образует угол 60° с осью цилиндра. Найти площадь полной поверхности и объем цилиндра. Треугольник АО1О прямоугольный, найдем АО и ОО1 по синусу и косинусу 60 ̊

9. Отрезок, соединяющий центр верхнего основания цилиндра с точкой окружности нижнего основания, равен 8 см и образует угол 60° с осью цилиндра. Найти площадь полной поверхности и объем цилиндра. Треугольник АО1О прямоугольный, найдем АО и ОО1 по синусу и косинусу 60 ̊

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Международная дистанционная олимпиада Осень 2021

Вам будут интересны эти курсы:

Оставьте свой комментарий

Минобрнауки работает над изменением подходов к защите диплома

В школе в Пермском крае произошла стрельба

Минпросвещения намерено включить проверку иллюстраций в критерии экспертизы учебников

Школьников не планируют переводить на удаленку после каникул

Минобрнауки утвердило перечень олимпиад для школьников на 2021-2022 учебный год

В России запустили «Школу общественной дипломатии» для малочисленных народов

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

В цилиндре отрезок который соединяет центр верхнего основания цилиндра

В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки А и В, а на окружности другого основания — точки В₁ и С₁, причем ВВ₁ — образующая цилиндра, а отрезок АС₁ пересекает ось цилиндра.

а) Докажите, что угол АВС₁ прямой.

б) Найдите площадь боковой поверхности цилиндра, если AB = 20, BB₁ = 15, B₁C₁ = 21.

а) Рассмотрим плоскость, проходящую через ось цилиндра и прямую АС₁. Обозначим точку пересечения этой плоскости и окружности основания цилиндра, содержащую точку А, через точку С. Тогда СС₁ — образующая цилиндра. Отрезок АС пересекает ось цилиндра. Значит, он проходит через центр окружности основания цилиндра, то есть является ее диаметром. Следовательно, угол АВС прямой.

Прямая СС₁ является образующей цилиндра, поэтому она перпендикулярна прямой АВ. Таким образом, прямая АВ перпендикулярна плоскости ВСС₁б а значит, угол АВС₁ прямой.

б) Отрезок AC является диаметром основания цилиндра. Значит, длина

окружности основания цилиндра равна

Следовательно, площадь боковой поверхности цилиндра равна

Ответ: б)

В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки А и В, а на окружности другого основания — точки В₁ и С₁, причем ВВ₁ — образующая цилиндра, а отрезок АС₁ пересекает ось цилиндра.

а) Докажите, что угол АВС₁ прямой.

б) Найдите площадь боковой поверхности цилиндра, если AB = 15, BB₁ = 21, B₁C₁ = 20.

а) Рассмотрим плоскость, проходящую через ось цилиндра и прямую АС₁. Обозначим точку пересечения этой плоскости и окружности основания цилиндра, содержащую точку А, через точку С. Тогда СС₁ — образующая цилиндра. Отрезок АС пересекает ось цилиндра. Значит, он проходит через центр окружности основания цилиндра, то есть является ее диаметром. Следовательно, угол АВС прямой.

Прямая СС₁ является образующей цилиндра, поэтому она перпендикулярна прямой АВ. Таким образом, прямая АВ перпендикулярна плоскости ВСС₁б а значит, угол АВС₁ прямой.

б) Отрезок AC является диаметром основания цилиндра. Значит, длина

окружности основания цилиндра равна

Следовательно, площадь боковой поверхности цилиндра равна

Ответ: б)

Аналоги к заданию № 520938: 520945 Все

В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки A, B и C, а на окружности другого основания — точка C₁, причём CC₁ — образующая цилиндра, а AC&nbsp— диаметр основания. Известно,что

а) Докажите, что угол между прямыми и равен

а) Пусть BB₁ — образующая цилиндра. Тогда BB₁C₁C — прямоугольник, поэтому угол между прямыми AC₁ и BС равен углу

Угол ABC опирается на диаметр основания цилиндра, поэтому он прямой. Значит, прямая B₁C₁, параллельная прямой BС, перпендикулярна прямым AB и BB₁. Таким образом, прямая B₁С₁ перпендикулярна плоскости ABB₁, а значит, угол AB₁C₁ прямой.

В прямоугольном треугольнике АB₁С₁:

Значит,

б) Отрезок AC является диаметром основания цилиндра. Значит, площадь основания цилиндра

Следовательно, объём цилиндра

Ответ: б)

В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки А и В, а на окружности другого основания — точки В₁ и С₁, причем ВВ₁ — образующая цилиндра, а отрезок АС₁ пересекает ось цилиндра.

а) Докажите, что угол АВС₁ прямой.

а) Рассмотрим плоскость, проходящую через ось цилиндра и прямую АС₁. Обозначим точку пересечения этой плоскости и окружности основания цилиндра, содержащую точку А, через точку С. Тогда СС₁ — образующая цилиндра. Отрезок АС пересекает ось цилиндра. Значит, он проходит через центр окружности основания цилиндра, то есть является ее диаметром. Следовательно, угол АВС прямой.

Прямая СС₁ является образующей цилиндра, поэтому она перпендикулярна прямой АВ. Таким образом, прямая АВ перпендикулярна двум пересекающимся прямым, лежащим в плоскости ВСС₁ (BС и СС₁), а значит, прямая АВ перпендикулярна плоскости ВСС₁ и любой прямой, лежащей в этой плоскости, в том числе и ВС₁. Значит, угол АВС₁ прямой.

б) Поскольку прямые ВВ₁ и СС₁ параллельны, искомый угол равен углу АС₁С.

Треугольники АВС и АСС₁ являются прямоугольными, поэтому:

;

Ответ:

Приведем другой способ решений.

a) Введем систему координат, как показано на рисунке. Найдем координаты точек A, B и C₁. Пусть а радиус основания — r, тогда

Найдем координаты векторов и

Найдем скалярное произведение векторов и

В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки А и В, а на окружности другого основания — точки В₁ и С₁, причем ВВ₁ — образующая цилиндра, а отрезок АС₁ пересекает ось цилиндра.

а) Докажите, что угол АВС₁ прямой.

а) Рассмотрим плоскость, проходящую через ось цилиндра и прямую АС₁. Обозначим точку пересечения этой плоскости и окружности основания цилиндра, содержащую точку А, через точку С. Тогда СС₁ — образующая цилиндра. Отрезок АС пересекает ось цилиндра. Значит, он проходит через центр окружности основания цилиндра, то есть является ее диаметром. Следовательно, угол АВС прямой.

Прямая СС₁ является образующей цилиндра, поэтому она перпендикулярна прямой АВ. Таким образом, прямая АВ перпендикулярна двум пересекающимся прямым, лежащим в плоскости ВСС₁ (BС и СС₁), а значит, прямая АВ перпендикулярна плоскости ВСС₁ и любой прямой, лежащей в этой плоскости. Значит, угол АВС₁ прямой.

б) Поскольку прямые ВВ₁ и СС₁ параллельны, искомый угол равен углу АС₁С.

Треугольники АВС и АСС₁ являются прямоугольными, поэтому:

;

Ответ:

Приведем другой способ решений.

a) Введем систему координат, как показано на рисунке. Найдем координаты точек A, B и C₁. Пусть а радиус основания — r, тогда

Найдем координаты векторов и

Найдем длины векторов и

Найдем косинус угла между этими векторами:

Значит, угол АВС₁ прямой.

Аналоги к заданию № 520803: 520853 520879 520915 Все

Диаметр окружности основания цилиндра равен 20, образующая цилиндра равна 28. Плоскость пересекает его основания по хордам длины 12 и 16. Расстояние между этими хордами равно

а) Докажите, что центры оснований цилиндра лежат по одну сторону от этой плоскости.

б) Найдите угол между этой плоскостью и плоскостью основания цилиндра.

а) Заметим, что хорда длиной 12 находится на расстоянии от центра окружности основания, а хорда длиной 16, аналогично, — на расстоянии 6. Поэтому расстояние между их проекциями на плоскость, параллельную основаниям цилиндров, составляет либо 8 + 6 = 14, либо 8 − 6 = 2. Тогда расстояние между хордами составляет либо либо По условию реализовался второй случай, в нем проекции хорд лежат по одну сторону от оси цилиндра. Значит, ось не пересекает данную плоскость в пределах цилиндра, то есть основания лежат по одну сторону от нее.

б) Обозначим центры оснований за и Проведем из центра основания с хордой длины 12 серединный перпендикуляр к этой хорде (он имеет длину 8, как уже отмечалось) и из центра другого основания — к другой хорде. Они лежат в одной плоскости перпендикулярной этим хордам. Назовем середину меньшей хорды B, большей A и проекцию A на второе основание —

Тогда и, значит, AB, AH перпендикулярны хорде, то есть прямой пересечения основания с данной плоскостью.

Значит, искомый угол равен

Ответ:

Диаметр окружности основания цилиндра равен 26, образующая цилиндра равна 21. Плоскость пересекает его основания по хордам длины 24 и 10. Расстояние между этими хордами равно

а) Докажите, что центры оснований цилиндра лежат по разные стороны от этой плоскости.

б) Найдите тангенс угла между этой плоскостью и плоскостью основания цилиндра.

а) Заметим, что хорда длиной 24 находится на расстоянии от центра окружности основания, а хорда длиной 10, аналогично, — на расстоянии 12. Поэтому расстояние между их проекциями на плоскость, параллельную основаниям цилиндров, составляет либо 5+12=17, либо 12-5=7. Тогда расстояние между хордами составляет либо либо По условию реализовался первый случай, в нем проекции хорд лежат по разные стороны от оси цилиндра. Значит, ось пересекает данную плоскость в пределах цилиндра, то есть центры оснований лежат по разные стороны от нее.

б) Обозначим центры оснований за и Проведем из центра основания с хордой длины 24 серединный перпендикуляр к этой хорде (он имеет длину 5, как уже отмечалось) и из центра другого основания — к другой хорде. Они лежат в одной плоскости перпендикулярной этим хордам. Назовем середину меньшей хорды B, большей A и проекцию A на второе основание —

Тогда и, значит, AB, AH перпендикулярны хорде, то есть прямой пересечения основания с данной плоскостью.

Значит искомый угол это

Ответ:

Аналоги к заданию № 513259: 514721 Все

В конус вписан цилиндр так, что нижнее основание цилиндра лежит на основании конуса, а окружность верхнего основания принадлежит боковой поверхности конуса. Объем конуса равен 72.

а) Найти объем цилиндра, верхнее основание которого делит высоту конуса пополам.

б) Найти наибольший объем вписанного цилиндра.

а) Обозначим радиус основания конуса за высоту за за и — радиус и высоту цилиндра. Проведем осевое сечение конуса. В нем верхнее основание цилиндра будет средней линией треугольника, поэтому радиус цилиндра вдвое меньше радиуса конуса. Высота цилиндра — тоже половина высоты конуса. Объем конуса равен:

б) В осевом сечении образуются два подобных треугольник (см. рисунок). Значит,

Значит, Объем цилиндра равен:

Нужно максимизировать Возьмем производную по

Крайние значения можно не проверять ( или там объем равен нулю). Имеем:

В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки А и В, а на окружности другого основания — точки В₁ и С₁, причем ВВ₁ — образующая цилиндра, а отрезок АС₁ пересекает ось цилиндра.

а) Докажите, что угол АВС₁ прямой.

а) Рассмотрим плоскость, проходящую через ось цилиндра и прямую АС₁. Обозначим точку пересечения этой плоскости и окружности основания цилиндра, содержащую точку А, через точку С. Тогда СС₁ — образующая цилиндра. Отрезок АС пересекает ось цилиндра. Значит, он проходит через центр окружности основания цилиндра, то есть является ее диаметром. Следовательно, угол АВС прямой.

Прямая СС₁ является образующей цилиндра, поэтому она перпендикулярна прямой АВ. Таким образом, прямая АВ перпендикулярна двум пересекающимся прямым, лежащим в плоскости ВСС₁ (BС и СС₁), а значит, прямая АВ перпендикулярна плоскости ВСС₁ и любой прямой, лежащей в этой плоскости. Значит, угол АВС₁ прямой.

б) Треугольник ABC₁ прямоугольный, поэтому искомое расстояние равно его высоте h, проведённой к гипотенузе. Получаем:

Ответ: б)

Аналоги к заданию № 520803: 520853 520879 520915 Все

В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки А и В, а на окружности другого основания — точки В₁ и С₁, причем ВВ₁ — образующая цилиндра, а отрезок АС₁ пересекает ось цилиндра.

а) Докажите, что угол АВС₁ прямой.

а) Рассмотрим плоскость, проходящую через ось цилиндра и прямую АС₁. Обозначим точку пересечения этой плоскости и окружности основания цилиндра, содержащую точку А, через точку С. Тогда СС₁ — образующая цилиндра. Отрезок АС пересекает ось цилиндра. Значит, он проходит через центр окружности основания цилиндра, то есть является ее диаметром. Следовательно, угол АВС прямой.

Прямая СС₁ является образующей цилиндра, поэтому она перпендикулярна прямой АВ. Таким образом, прямая АВ перпендикулярна двум пересекающимся прямым, лежащим в плоскости ВСС₁ (BС и СС₁), а значит, прямая АВ перпендикулярна плоскости ВСС₁ и любой прямой, лежащей в этой плоскости. Значит, угол АВС₁ прямой.

б) Треугольник ABC₁ прямоугольный, поэтому искомое расстояние равно его высоте h, проведённой к гипотенузе. Получаем:

Аналоги к заданию № 520803: 520853 520879 520915 Все

Цилиндр и конус имеют общее основание, вершина конуса является центром другого основания цилиндра. Каждая образующая конуса наклонена к плоскости основания под углом 30°.

а) Докажите, что площади боковых поверхностей цилиндра и конуса равны

б) Найдите радиус сферы, касающейся боковых поверхностей цилиндра и конуса, а так

же одного из оснований цилиндра, если известно, что объем конуса равен

а) Пусть радиус основания цилиндра равен а высота Тогда тангенс угла наклона образующей есть откуда и образующая конуса равна Вычислим теперь площади боковой поверхности цилиндра и конуса. Это и что и требовалось доказать.

б) Рассмотрим сечение цилиндра и конуса осевой плоскость, проходящей через центр сферы. Все точки касания будут лежать в этой плоскости. В сечении получим окружность, вписанную в прямоугольный треугольник со сторонами поэтому ее радиус равен

C другой стороны, как мы знаем,

откуда поэтому искомый радиус равен 1.

В одном основании прямого кругового цилиндра с высотой 12 и радиусом основания 6 проведена хорда AB, равная радиусу основания, а в другом его основании проведён диаметр CD, перпендикулярный AB. Построено сечение ABNM, проходящее через прямую AB перпендикулярно прямой CD так, что точка C и центр основания цилиндра, в котором проведён диаметр CD, лежат с одной стороны от сечения.

а) Докажите, что диагонали этого сечения равны между собой.

б) Найдите объём пирамиды CABNM.

а) Так сечение перпендикулярно прямой CD, то оно перпендикулярно основанию цилиндра содержащему эту прямую. Для построения сечения опустим перпендикуляры AM и BN на второе основание цилиндра. Отрезки AM и BN параллельны и равны, значит, ABNM — параллелограмм. Так как прямые AM и BN перпендикулярны основаниям цилиндра и, в частности, прямой AB, параллелограмм ABNM является прямоугольником. Диагонали прямоугольника равны, что и требовалось доказать.

б) Площадь прямоугольника ABNM равна Отрезок OH равен Высота CH пирамиды CABNM равна Следовательно, объём пирамиды CABNM равен

Ответ: б)

AB — диаметр нижнего основания цилиндра, а CD — хорда верхнего основания цилиндра, причём CD || AB.

а) Докажите, что отрезки AC и BD равны.

б) Найдите объём пирамиды, основанием которой является четырёхугольник с вершинами в точках A, B, C, D, а вершиной — центр верхнего основания цилиндра, если известно, что высота цилиндра равна 9, AB = 26, CD = 10.

а) Рассмотрим — проекцию AB на плоскость верхнего основания. Тогда поэтому точки служат вершинами вписанной трапеции. Но такая трапеция обязательно равнобедренная, поэтому ее боковые стороны и диагонали равны, то есть Обозначая за h высоту цилиндра, имеем

б) Будем считать, что точки лежат именно в таком порядке (иначе переименуем точки C и D). Опустим перпендикуляр OH на CD. Заметим, что поэтому Обозначая за центр нижнего основания цилиндра, находим — высота трапеции ACDB.

Опустим перпендикуляр из O на Он будет также перпендикулярен CD (поскольку то и плоскость в которой он лежит, перпендикулярна CD).

Значит, это и будет высота пирамиды. Теперь считаем

Дан прямой круговой цилиндр высотой 9 и радиусом 2. В одном из оснований проведена хорда AB, равная радиусу основания, а в другом основании проведён диаметр CD, перпендикулярный прямой AB. Построено сечение цилиндра плоскостью ABNM, перпендикулярной прямой CD, причём точка C и центр основания цилиндра, содержащего отрезок CD, лежат по одну сторону от плоскости сечения.

а) Докажите, что диагонали четырёхугольника ABNM равны.

б) Найдите объём пирамиды CABNM.

а) Плоскость сечения ABNM перпендикулярна прямой CD, поэтому отрезки AM и BN являются образующими цилиндра. Следовательно, отрезки AM и BN параллельны и равны, значит, ABNM — параллелограмм. Так как прямые AM и BN перпендикулярны основаниям цилиндра и, в частности, прямой AB, параллелограмм ABNM является прямоугольником. Отрезки AN и BM равны как диагонали прямоугольника, что и требовалось доказать.

б) Площадь прямоугольника ABNM равна Пусть H — точка пересечения отрезков NM и CD, O — центр основания цилиндра, содержащего отрезок CD. Отрезок OH равен Высота CH пирамиды CABNM равна Следовательно, объём пирамиды CABNM равен:

Ответ: б)

Дан прямой круговой цилиндр высотой 3 и радиусом 8. В одном из оснований проведена хорда AB, равная радиусу основания, а в другом основании проведён диаметр CD, перпендикулярный прямой AB. Построено сечение цилиндра плоскостью ABNM, перпендикулярной прямой CD, причём точка C и центр основания цилиндра, содержащего отрезок CD, лежат по одну сторону от плоскости сечения.

а) Докажите, что диагонали четырёхугольника ABNM равны.

б) Найдите объём пирамиды CABNM.

а) Плоскость сечения ABNM перпендикулярна прямой CD, поэтому отрезки AM и BN являются образующими цилиндра. Следовательно, отрезки AM и BN параллельны и равны, значит, ABNM — параллелограмм. Так как прямые AM и BN перпендикулярны основаниям цилиндра и, в частности, прямой AB, параллелограмм ABNM является прямоугольником. Отрезки AN и BM равны как диагонали прямоугольника, что и требовалось доказать.

б) Площадь прямоугольника ABNM равна Пусть H — точка пересечения отрезков NM и CD, O — центр основания цилиндра, содержащего отрезок CD. Отрезок OH равен Высота CH пирамиды CABNM равна Следовательно, объём пирамиды CABNM равен:

Ответ: б)

Высота цилиндра равна 3. Равнобедренный треугольник ABC с боковой стороной 10 и ∠A = 120° расположен так, что его вершина A лежит на окружности нижнего основания цилиндра, а вершины B и C — на окружности верхнего основания.

а) Найдите угол между плоскостью ABC и плоскостью основания цилиндра.

б) Докажите, что радиус основания цилиндра больше, чем .

а) Пусть AA₁ — образующая цилиндра, M — середина хорды BC. Тогда

В равнобедренных треугольниках BAC и BA₁C медианы AM и A₁M являются высотами. Поэтому искомый угол между плоскостями равен углу ∠AMA₁. В прямоугольном треугольнике AMA₁ имеем:

Ответ:

б) Из пункта а) получаем, что , , значит . Тогда . Пусть R — радиус основания цилиндра. Тогда, по теореме синусов . Отсюда . Что и требовалось доказать.

Нет ни малейшего намека на то, где именно точка А касается нижнего оснвоания. Она может касаться ровно в центе окружности основания, либо, как у вас, на длине окружности.

По каким, так сказать, подсказкам вы определили, что точка А именно там, где она и есть?

Внимательнее читайте условие задачи («вершина A лежит на окружности нижнего основания цилиндра»).

Диаметр окружности основания цилиндра равен 26, образующая цилиндра равна 21. Плоскость пересекает его основания по хордам длины 24 и 10. Расстояние между этими хордами равно

а) Докажите, что центры оснований цилиндра лежат по разные стороны от этой плоскости.

б) Найдите угол между этой плоскостью и плоскостью основания цилиндра.

Сразу отметим, что в окружности радиуса R расстояние от центра до хорды (то есть до середины хорды) длиной равно Поэтому расстояния от центров оснований до хорд равны 5 и 12.

а) Пусть A и — середины хорд, B — проекция на другое основание цилиндра. Тогда поэтому следует выбирать знак что как раз и означает, что хорды лежат по разные стороны от центров оснований, поэтому центры лежат по разные стороны от плоскости.

б) Указанные две плоскости пересекаются по хорде, содержащей точку A, при этом AB перпендикулярна этой хорде, следовательно, и тоже. Поэтому

Ответ: б)

В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки A, B и C, а на окружности другого основания — точка C₁ причём CC₁ — образующая цилиндра, а AC — диаметр основания. Известно, что

а) Докажите, что угол между прямыми BC и AC₁ равен

б) Найдите расстояние от точки B до AC₁.

а) Пусть — образующая цилиндра. Тогда — прямоугольник, поэтому угол между прямыми и равен углу

Угол ABC опирается на диаметр основания цилиндра, поэтому он прямой. Значит, прямая параллельная прямой перпендикулярная прямым и Таким образом, прямая перпендикулярна плоскости а значит, угол прямой.

В прямоугольном треугольнике :

Тогда Таким образом, гипотенуза AC₁ прямоугольного треугольника AB₁C₁ вдвое больше катета. Следовательно, а искомый

б) Наклонная C₁B перпендикулярна прямой AB по теореме о трёх перпендикулярах. Тогда треугольник АВС₁ прямоугольный, а искомое расстояние равно длине высоты, проведенной из вершины прямого угла треугольника ABC₁ к гипотенузе АС₁. Она равна

Ответ: