Собственные вектора матрицы лапласа

Дата публикации Feb 21, 2019

Видео:Собственные векторы и собственные значения матрицыСкачать

Введение

В этом посте мы рассмотрим тонкости спектральной кластеризации для графиков и других данных. Кластеризация является одной из главных задач в машинном обучении без учителя. Цель состоит в том, чтобы назначить немаркированные данные группам, где, возможно, аналогичные точки данных будут назначены в одну группу.

Спектральная кластеризация — это метод с корнями в теории графов, где этот подход используется для идентификации сообществ узлов в графе на основе соединяющих их ребер. Этот метод является гибким и позволяет кластеризовать не графовые данные.

Спектральная кластеризация использует информацию из собственных значений (спектра) специальных матриц, построенных из графика или набора данных. Мы узнаем, как построить эти матрицы, интерпретировать их спектр и использовать собственные векторы для назначения наших данных кластерам.

Видео:Собственные векторы и собственные числа линейного оператораСкачать

Собственные векторы и собственные значения

Критическим для этой дискуссии является концепция собственных значений и собственные векторы. Для матрицы A, если существует вектор x, который не является всеми 0 и скалярным λ, таким, что Ax = λx, то x называется собственным вектором A с соответствующим собственным значением λ.

Мы можем думать о матрице A как о функции, которая отображает векторы на новые векторы. Большинство векторов окажутся где-то совершенно разными, когда к ним будет применен A, но собственные векторы меняются только по величине. Если вы проведете линию через начало координат и собственный вектор, то после отображения собственный вектор все равно попадет на линию. Величина, по которой вектор масштабируется вдоль линии, зависит от λ.

Мы можем легко найти собственные значения и собственные векторы матрицы, используя numpy в Python:

Собственные векторы являются важной частью линейной алгебры, потому что они помогают описать динамику систем, представленных матрицами. Существует множество приложений, в которых используются собственные векторы, и мы будем использовать их непосредственно здесь для выполнения спектральной кластеризации.

Видео:Собственные значения и собственные векторы матрицы (4)Скачать

диаграммы

Графики являются естественным способом представления многих типов данных. Граф — это набор узлов с соответствующим набором ребер, которые соединяют узлы. Края могут быть направленными или ненаправленными и даже иметь веса, связанные с ними.

Сеть роутеров в интернете легко представить в виде графика. Маршрутизаторы — это узлы, а ребра — это соединения между парами маршрутизаторов. Некоторые маршрутизаторы могут разрешать трафик только в одном направлении, поэтому границы могут быть направлены в направлении направления трафика. Веса на краях могут представлять полосу пропускания, доступную вдоль этого края. При такой настройке мы могли бы затем запросить график, чтобы найти эффективные пути для передачи данных от одного маршрутизатора к другому по сети.

Давайте использовать следующий неориентированный граф в качестве рабочего примера:

Этот граф имеет 10 узлов и 12 ребер. Он также имеет два соединенных компонента и . Связанный компонент — это максимальный подграф узлов, у всех из которых есть пути к остальным узлам подграфа.

Связанные компоненты кажутся важными, если наша задача — назначить эти узлы сообществам или кластерам. Простая идея — сделать каждый связанный компонент отдельным кластером. Это кажется разумным для нашего примера графа, но возможно, что весь граф может быть связан, или что связанные компоненты очень велики. Могут также быть меньшие структуры в связанном компоненте, которые являются хорошими кандидатами для сообществ. Вскоре мы увидим важность идеи связанного компонента для спектральной кластеризации.

Видео:Собственные векторы и собственные числа линейного оператораСкачать

Матрица смежности

Мы можем представить наш примерный граф в виде матрицы смежности, где индексы строк и столбцов представляют узлы, а записи представляют отсутствие или наличие ребра между узлами. Матрица смежности для нашего примера графа выглядит следующим образом:

В матрице мы видим, что строка 0, столбец 1 имеет значение 1. Это означает, что существует ребро, соединяющее узел 0 с узлом 1. Если ребра были взвешены, веса ребер были бы в этой матрице вместо только 1 и 0. Так как наш график не направлен, записи для строки i, col j будут равны записи в строке j, col i. Последнее, что следует отметить, это то, что диагональ этой матрицы равна 0, поскольку ни один из наших узлов не имеет ребер.

Видео:7 4 Собственные векторы и собственные значенияСкачать

Степень Матрица

Степень узла — это количество ребер, соединенных с ним. В ориентированном графе мы могли бы говорить о степени и степени, но в этом примере у нас просто есть степень, так как ребра идут в обе стороны. Глядя на наш график, мы видим, что узел 0 имеет степень 4, поскольку он имеет 4 ребра. Мы также можем получить степень, взяв сумму строки узла в матрице смежности.

Матрица степеней — это диагональная матрица, где значение на входе (i, i) является степенью узла i Давайте найдем матрицу степеней для нашего примера:

Сначала мы взяли сумму по оси 1 (строки) нашей матрицы смежности, а затем поместили эти значения в диагональную матрицу. Из матрицы степеней мы легко видим, что узлы 0 и 5 имеют 4 ребра, в то время как остальные узлы имеют только 2.

Видео:Диагональный вид матрицы. Приведение матрицы к диагональному виду. Собственные векторыСкачать

График лапласианский

Теперь мы собираемся вычислить граф Лапласа. Лапласиан — это просто еще одно матричное представление графа. У него есть несколько прекрасных свойств, которыми мы воспользуемся для спектральной кластеризации. Чтобы вычислить нормальный лапласиан (есть несколько вариантов), мы просто вычитаем матрицу смежности из нашей матрицы степеней:

Диагональ лапласиана — это степень наших узлов, а вне диагонали — вес отрицательного края. Это представление, которое мы ищем для выполнения спектральной кластеризации.

Видео:Собственные значения и собственные векторыСкачать

Собственные значения графа лапласиана

Как уже упоминалось, лапласиан обладает некоторыми прекрасными свойствами. Чтобы понять это, давайте рассмотрим собственные значения, связанные с лапласианом, когда я добавлю ребра в наш граф:

Мы видим, что когда граф полностью отключен, все десять наших собственных значений равны 0. Когда мы добавляем ребра, некоторые из наших собственных значений увеличиваются. Фактически, число собственных значений 0 соответствует числу связанных компонент в нашем графе!

Посмотрите внимательно, как добавлен этот последний край, соединяя два компонента в один. Когда это происходит, все собственные значения, кроме одного, были отменены:

Первое собственное значение равно 0, потому что у нас есть только один связный компонент (весь граф связен). Соответствующий собственный вектор всегда будет иметь постоянные значения (в этом примере все значения близки к 0,32).

Первое ненулевое собственное значение называется спектральной щелью. Спектральная щель дает нам некоторое представление о плотности графика. Если бы этот граф был плотно связан (все пары из 10 узлов имели ребро), то спектральный разрыв был бы 10.

Второе собственное значение называется значением Фидлера, а соответствующий вектор является вектором Фидлера. Значение Фидлера приблизительно соответствует минимальному срезу графа, необходимому для разделения графа на два связанных компонента. Напомним, что если бы в нашем графе уже было два связанных компонента, то значение Фидлера было бы равно 0. Каждое значение в векторе Фидлера дает нам информацию о том, какой стороне разреза принадлежит этот узел. Давайте раскрасим узлы в зависимости от того, положительна ли их запись в векторе Филдера:

Этот простой трюк разделил наш график на две группы! Почему это работает? Помните, что нулевые собственные значения представляют связанные компоненты. Собственные значения около нуля говорят нам, что существует почти разделение двух компонентов. Здесь у нас есть одно преимущество: если бы его не было, у нас было бы два отдельных компонента. Таким образом, второе собственное значение мало.

Подводя итог, что мы знаем до сих пор: первое собственное значение 0, потому что у нас есть один связанный компонент. Второе собственное значение около 0, потому что мы на расстоянии одного края от двух соединенных компонентов. Мы также видели, что вектор, связанный с этим значением, говорит нам, как разделить узлы на эти приблизительно связанные компоненты.

Возможно, вы заметили, что следующие два собственных значения также довольно малы. Это говорит нам о том, что мы «близки» к четырем отдельным подключенным компонентам. В общем, мы часто ищем первый большой разрыв между собственными значениями, чтобы найти число кластеров, выраженных в наших данных. Видите разрыв между собственными значениями четыре и пять?

Наличие четырех собственных значений перед разрывом указывает на то, что, вероятно, существует четыре кластера. Векторы, связанные с первыми тремя положительными собственными значениями, должны дать нам информацию о том, какие три разреза необходимо сделать на графике, чтобы назначить каждый узел одному из четырех приближенных компонентов. Давайте построим матрицу из этих трех векторов и выполним кластеризацию K-средних для определения назначений:

График был сегментирован на четыре квадранта, причем узлы 0 и 5 произвольно назначены одному из их связанных квадрантов. Это действительно круто, и это спектральная кластеризация!

Подводя итог, мы сначала взяли наш граф и построили матрицу смежности. Затем мы создали лапласиан графа, вычтя матрицу смежности из матрицы степеней. Собственные значения лапласиана указывали на наличие четырех кластеров. Векторы, связанные с этими собственными значениями, содержат информацию о том, как сегментировать узлы. Наконец, мы выполнили K-средства для этих векторов, чтобы получить метки для узлов. Далее мы увидим, как это сделать для произвольных данных.

Видео:А.7.35 Собственные вектора и собственные значения матрицыСкачать

Спектральная кластеризация произвольных данных

Посмотрите на данные ниже. Точки нарисованы из двух концентрических кругов с добавлением шума Нам бы хотелось, чтобы алгоритм позволял группировать эти точки в два круга, которые их генерировали.

Эти данные не в форме графика. Итак, во-первых, давайте просто попробуем алгоритм обрезки печенья, такой как K-Means. K-Means найдет два центроида и пометит точки, в зависимости от того, к какому центроиду они ближе всего. Вот результаты:

Очевидно, K-Means не собирался работать. Он действует на евклидовом расстоянии и предполагает, что скопления примерно сферические. Эти данные (и часто данные реального мира) нарушают эти предположения. Давайте попробуем решить эту проблему с помощью спектральной кластеризации.

Видео:Овчинников А. В. - Линейная алгебра - Собственные значения и собственные векторы линейного оператораСкачать

График ближайших соседей

Есть несколько способов обработать наши данные как график. Самый простой способ — построить граф k-ближайших соседей. Граф k-ближайших соседей обрабатывает каждую точку данных как узел в графе. Затем ребро рисуется от каждого узла до его k ближайших соседей в исходном пространстве. Как правило, алгоритм не слишком чувствителен к выбору k. Меньшие числа, такие как 5 или 10, обычно работают довольно хорошо.

Посмотрите на изображение данных еще раз и представьте, что каждая точка связана со своими 5 ближайшими соседями. Любая точка во внешнем кольце должна быть в состоянии следовать по пути вдоль кольца, но во внутреннем круге не будет никаких путей. Довольно легко увидеть, что этот график будет иметь два связанных компонента: внешнее кольцо и внутренний круг.

Поскольку мы разделяем эти данные только на два компонента, мы должны использовать наш векторный метод Фидлера ранее. Вот код, который я использовал для спектральной кластеризации этих данных:

И вот результаты:

Видео:Вычисление определителя четвертого порядка по теореме ЛапласаСкачать

Другие подходы

Граф ближайших соседей — хороший подход, но он основан на том факте, что «близкие» точки должны принадлежать одному кластеру. В зависимости от ваших данных, это может быть не так. Более общий подход заключается в построении аффинной матрицы. Матрица сходства похожа на матрицу смежности, за исключением того, что значение для пары точек показывает, насколько эти точки похожи друг на друга. Если пары точек сильно различаются, то сродство должно быть 0. Если точки идентичны, то сродство может быть 1. Таким образом, сродство действует как вес для ребер нашего графа.

Как решить, что означает совпадение двух точек данных, является одним из наиболее важных вопросов в машинном обучении. Часто знание предметной области — лучший способ построить меру подобия. Если у вас есть доступ к экспертам по доменам, задайте им этот вопрос.

Есть также целые поля, посвященные изучению того, как строить метрики подобия непосредственно из данных. Например, если у вас есть некоторые помеченные данные, вы можете обучить классификатор, чтобы предсказать, похожи ли два входа или нет, основываясь на том, имеют ли они одинаковую метку. Затем этот классификатор можно использовать для присвоения сходства парам немаркированных точек.

Видео:Айгенвектора и айгензначения | Сущность Линейной Алгебры, глава 10Скачать

Вывод

Мы рассмотрели теорию и применение спектральной кластеризации для графов и произвольных данных. Спектральная кластеризация — это гибкий подход для поиска кластеров, когда ваши данные не соответствуют требованиям других распространенных алгоритмов.

Сначала мы сформировали график между нашими точками данных. Края графика отражают сходство точек. Собственные значения графа лапласиана могут затем использоваться для поиска наилучшего числа кластеров, а собственные векторы могут использоваться для поиска фактических меток кластеров.

Я надеюсь, что вам понравился этот пост, и вы нашли спектральную кластеризацию полезной в вашей работе или исследовании.

Видео:Собственные значения матрицыСкачать

Методы решения задач о собственных
значениях и векторах матриц

Видео:Собственные векторы и собственные значенияСкачать

Постановка задачи

Пусть [math]A[/math] — действительная числовая квадратная матрица размера [math](ntimes n)[/math] . Ненулевой вектор [math]X= bigl(x_1,ldots,x_nbigr)^T[/math] размера [math](ntimes1)[/math] , удовлетворяющий условию

называется собственным вектором матрицы [math]A[/math] . Число [math]lambda[/math] в равенстве (2.1) называется собственным значением. Говорят, что собственный вектор [math]X[/math] соответствует (принадлежит) собственному значению [math]lambda[/math] .

Равенство (2.1) равносильно однородной относительно [math]X[/math] системе:

Система (2.2) имеет ненулевое решение для вектора [math]X[/math] (при известном [math]lambda[/math] ) при условии [math]|A-lambda E|=0[/math] . Это равенство есть характеристическое уравнение:

где [math]P_n(lambda)[/math] — характеристический многочлен n-й степени. Корни [math]lambda_1, lambda_2,ldots,lambda_n[/math] характеристического уравнения (2.3) являются собственными (характеристическими) значениями матрицы [math]A[/math] , а соответствующие каждому собственному значению [math]lambda_i,

i=1,ldots,n[/math] , ненулевые векторы [math]X^i[/math] , удовлетворяющие системе

являются собственными векторами.

Требуется найти собственные значения и собственные векторы заданной матрицы. Поставленная задача часто именуется второй задачей линейной алгебры.

Проблема собственных значений (частот) возникает при анализе поведения мостов, зданий, летательных аппаратов и других конструкций, характеризующихся малыми смещениями от положения равновесия, а также при анализе устойчивости численных схем. Характеристическое уравнение вместе с его собственными значениями и собственными векторами является основным в теории механических или электрических колебаний на макроскопическом или микроскопическом
уровнях.

Различают полную и частичную проблему собственных значений, когда необходимо найти весь спектр (все собственные значения) и собственные векторы либо часть спектра, например: [math]rho(A)= max_|lambda_i(A)|[/math] и [math]min_|lambda_i(A)|[/math] . Величина [math]rho(A)[/math] называется спектральным радиусом .

1. Если для собственного значения [math]lambda_i[/math] — найден собственный вектор [math]X^i[/math] , то вектор [math]mu X^i[/math] , где [math]mu[/math] — произвольное число, также является собственным вектором, соответствующим этому же собственному значению [math]lambda_i[/math] .

2. Попарно различным собственным значениям соответствуют линейно независимые собственные векторы; k-кратному корню характеристического уравнения соответствует не более [math]k[/math] линейно независимых собственных векторов.

3. Симметрическая матрица имеет полный спектр [math]lambda_i,

i=overline[/math] , действительных собственных значений; k-кратному корню характеристического уравнения симметрической матрицы соответствует ровно [math]k[/math] линейно независимых собственных векторов.

4. Положительно определенная симметрическая матрица имеет полный спектр действительных положительных собственных значений.

Видео:Матрицы и векторыСкачать

Метод непосредственного развертывания

Полную проблему собственных значений для матриц невысокого порядка [math](nleqslant10)[/math] можно решить методом непосредственного развертывания. В этом случае будем иметь

Уравнение [math]P_n(lambda)=0[/math] является нелинейным (методы его решения изложены в следующем разделе). Его решение дает [math]n[/math] , вообще говоря, комплексных собственных значений [math]lambda_1,lambda_2,ldots,lambda_n[/math] , при которых [math]P_n(lambda_i)=0

(i=overline)[/math] . Для каждого [math]lambda_i[/math] может быть найдено решение однородной системы [math](A-lambda_iE)X^i=0,

i=overline[/math] . Эти решения [math]X^i[/math] , определенные с точностью до произвольной константы, образуют систему [math]n[/math] , вообще говоря, различных векторов n-мерного пространства. В некоторых задачах несколько этих векторов (или все) могут совпадать.

Видео:Собственные значения и собственные векторы. ТемаСкачать

Алгоритм метода непосредственного развертывания

1. Для заданной матрицы [math]A[/math] составить характеристическое уравнение (2.5): [math]|A-lambda E|=0[/math] . Для развертывания детерминанта [math]|A-lambda E|[/math] можно использовать различные методы, например метод Крылова, метод Данилевского или другие методы.

2. Решить характеристическое уравнение и найти собственные значения [math]lambda_1, lambda_2, ldots,lambda_n[/math] . Для этого можно применить методы, изложенные далее.

3. Для каждого собственного значения составить систему (2.4):

и найти собственные векторы [math]X^i[/math] .

Замечание. Каждому собственному значению соответствует один или несколько векторов. Поскольку определитель [math]|A-lambda_iE|[/math] системы равен нулю, то ранг матрицы системы меньше числа неизвестных: [math]operatorname(A-lambda_iE)=r и в системе имеется ровно [math]r[/math] независимых уравнений, а [math](n-r)[/math] уравнений являются зависимыми. Для нахождения решения системы следует выбрать [math]r[/math] уравнений с [math]r[/math] неизвестными так, чтобы определитель составленной системы был отличен от нуля. Остальные [math](n-r)[/math] неизвестных следует перенести в правую часть и считать параметрами. Придавая параметрам различные значения, можно получить различные решения системы. Для простоты, как правило, попеременно полагают значение одного параметра равным 1, а остальные равными 0.

Пример 2.1. Найти собственные значения и собственные векторы матрицы [math]Ain mathbb^[/math] , где [math]A=begin3&-2\-4&1end[/math] .

1. Запишем уравнение (2.5): [math]|A-lambda E|= begin3-lambda&-2\-4& 1-lambda end= lambda^2-4 lambda-5=0[/math] , отсюда получаем характеристическое уравнение [math]P_2(lambda)equiv lambda^2-4 lambda-5=0[/math] .

2. Находим его корни (собственные значения): [math]lambda_1=5,

3. Составим систему [math](A-lambda_iE)X^i=0,

i=1,2[/math] , для каждого собственного
значения и найдем собственные векторы:

Отсюда [math]x_1^1=-x_2^1[/math] . Если [math]x_2^1=mu[/math] , то [math]x_1^1=-mu[/math] . В результате получаем [math]X^1= bigl^T= bigl^T[/math] .

Для [math]lambda_2=-1[/math] имеем

Отсюда [math]x_2^2=2x_1^2[/math] . Если [math]x_1^2=mu[/math] , то [math]x_2^2=2mu[/math] . В результате получаем [math]X^2= bigl^T= bigl^T[/math] , где [math]mu[/math] — произвольное действительное число.

Пример 2.2. Найти собственные значения и собственные векторы матрицы [math]A= begin2&-1&1\-1&2&-1\0&0&1end[/math] .

1. Запишем характеристическое уравнение (2.5):

2. Корни характеристического уравнения: [math]lambda_=1[/math] (кратный корень), [math]lambda_3=3[/math] — собственные значения матрицы.

3. Найдем собственные векторы.

Для [math]lambda_=1[/math] запишем систему [math](A-lambda_E)cdot X^=0colon[/math]

Поскольку [math]operatorname(A-lambda_E)=1[/math] , в системе имеется одно независимое уравнение

x_3^=3[/math] , получаем [math]x_1^=1[/math] и собственный вектор [math]X^1= begin1&1&0end^T[/math] .

x_3^=1[/math] , получаем [math]x_1^=-1[/math] и другой собственный вектор [math]X^2= begin-1&0&1end^T[/math] . Заметим, что оба собственных вектора линейно независимы.

Для собственного значения [math]lambda_3=3[/math] запишем систему [math](A-lambda_3E)cdot X^3=0colon[/math]

Поскольку [math]operatorname(A-lambda_3E)=2[/math] , то выбираем два уравнения:

x_1^3=-x_2^3[/math] . Полагая [math]x_2^3=1[/math] , получаем [math]x_1^3=-1[/math] и собственный вектор [math]X^3=begin-1&1&0 end^T[/math] .

Видео:Квантовая механика 8 - Операторы. Собственные векторы и собственные значения.Скачать

Метод итераций для нахождения собственных значений и векторов

Для решения частичной проблемы собственных значений и собственных векторов в практических расчетах часто используется метод итераций (степенной метод). На его основе можно определить приближенно собственные значения матрицы [math]A[/math] и спектральный радиус [math]rho(A)= max_bigl|lambda_i(A)bigr|[/math] .

Пусть матрица [math]A[/math] имеет [math]n[/math] линейно независимых собственных векторов [math]X^i,

i=1,ldots,n[/math] , и собственные значения матрицы [math]A[/math] таковы, что

Видео:Собственные значения и собственные вектора матричного оператораСкачать

Алгоритм метода итераций

1. Выбрать произвольное начальное (нулевое) приближение собственного вектора [math]X^[/math] (второй индекс в скобках здесь и ниже указывает номер приближения, а первый индекс без скобок соответствует номеру собственного значения). Положить [math]k=0[/math] .

lambda_1^= frac<x_i^><x_i^>[/math] , где [math]i[/math] — любой номер [math]1leqslant ileqslant n[/math] , и положить [math]k=1[/math] .

4. Найти [math]lambda_1^= frac<x_i^><x_i^>[/math] , где [math]x_i^, x_i^[/math] — соответствующие координаты векторов [math]X^[/math] и [math]X^[/math] . При этом может быть использована любая координата с номером [math]i,

1leqslant ileqslant n[/math] .

5. Если [math]Delta= bigl|lambda_1^- lambda_1^bigr|leqslant varepsilon[/math] , процесс завершить и положить [math]lambda_1cong lambda_1^[/math] . Если varepsilon»>[math]Delta>varepsilon[/math] , положить [math]k=k+1[/math] и перейти к пункту 3.

1. Процесс последовательных приближений

сходится, т.е. при [math]xtoinfty[/math] вектор [math]X^[/math] стремится к собственному вектору [math]X^1[/math] . Действительно, разложим [math]X^[/math] по всем собственным векторам: [math]textstyle<X^= sumlimits_^ c_iX^i>[/math] . Так как, согласно (2.4), [math]AX^i= lambda_iX^i[/math] , то

При большом [math]k[/math] дроби [math]<left(fracright)!>^k, ldots, <left(fracright)!>^k[/math] малы и поэтому [math]A^kX^= c_1lambda_1^kX^1[/math] , то есть [math]X^to X^1[/math] при [math]ktoinfty[/math] . Одновременно [math]lambda_1= limlimits_ frac<x_^><x_^>[/math] .

2. Вместо применяемой в пункте 4 алгоритма формулы для [math]lambda_1^[/math] можно взять среднее арифметическое соответствующих отношений для разных координат.

3. Метод может использоваться и в случае, если наибольшее по модулю собственное значение матрицы [math]A[/math] является кратным, т.е.

4. При неудачном выборе начального приближения [math]X^[/math] предел отношения [math]frac<x_i^><x_i^>[/math] может не существовать. В этом случае следует задать другое начальное приближение.

5. Рассмотренный итерационный процесс для [math]lambda_1[/math] сходится линейно, с параметром [math]c=frac[/math] и может быть очень медленным. Для его ускорения используется алгоритм Эйткена.

6. Если [math]A=A^T[/math] (матрица [math]A[/math] симметрическая), то сходимость процесса при определении [math]rho(A)[/math] может быть ускорена.

7. Используя [math]lambda_1[/math] , можно определить следующее значение [math]lambda_2[/math] по формуле [math]lambda_2= frac<x_i^- lambda_1 x_i^><x_i^- lambda_1 x_i^>

(i=1,2,ldots,n)[/math] . Эта формула дает грубые значения для [math]lambda_2[/math] , так как значение [math]lambda_1[/math] является приближенным. Если модули всех собственных значений различны, то на основе последней формулы можно вычислять и остальные [math]lambda_j

8. После проведения нескольких итераций рекомендуется «гасить» растущие компоненты получающегося собственного вектора. Это осуществляется нормировкой вектора, например, по формуле [math]frac<X^><|X^|_1>[/math] .

Пример 2.3. Для матрицы [math]A=begin5&1&2\ 1&4&1\ 2&1&3 end[/math] найти спектральный радиус степенным методом с точностью [math]varepsilon=0,,1[/math] .

1. Выбирается начальное приближение собственного вектора [math]X^= begin 1&1&1 end^T[/math] . Положим [math]k=0[/math] .

5. Так как varepsilon»>[math]bigl|lambda_1^- lambda_1^bigr|= 0,!75> varepsilon[/math] , то процесс необходимо продолжить. Результаты вычислений удобно представить в виде табл. 10.10.

Точность по достигнута на четвертой итерации. Таким образом, в качестве приближенного значения [math]lambda_1[/math] берется 6,9559, а в качестве собственного вектора принимается [math]X^1= begin 2838& 1682& 1888end^T[/math] .

Так как собственный вектор определяется с точностью до постоянного множителя, то [math]X^1[/math] лучше пронормировать, т.е. поделить все его компоненты на величину нормы. Для рассматриваемого примера получим

Согласно замечаниям, в качестве собственного значения [math]lambda_1[/math] матрицы можно взять не только отношение

а также их среднее арифметическое [math]fracapprox 6,!8581[/math] .

Пример 2.4. Найти максимальное по модулю собственное значение матрицы [math]A=begin2&-1&1\ -1&2&-1\ 0&0&3 end[/math] и соответствующий собственный вектор.

1. Зададим начальное приближение [math]X^= begin1&-1&1 end^T[/math] и [math]varepsilon=0,!0001[/math] .

Выполним расчеты согласно методике (табл. 10.11).

В результате получено собственное значение [math]lambda_1cong 3,!00003[/math] и собственный вектор [math]X^1= begin 88573&-88573&1end^T[/math] или после нормировки

Видео:Собственные значения и собственные векторы. ПримерСкачать

Метод вращений для нахождения собственных значений

Метод используется для решения полной проблемы собственных значений симметрической матрицы и основан на преобразовании подобия исходной матрицы [math]Ainmathbb^[/math] с помощью ортогональной матрицы [math]H[/math] .

Напомним, что две матрицы [math]A[/math] и [math]A^[/math] называются подобными ( [math]Asim A^[/math] или [math]A^sim A[/math] ), если [math]A^=H^AH[/math] или [math]A=HA^H^[/math] , где [math]H[/math] — невырожденная матрица.

В методе вращений в качестве [math]H[/math] берется ортогональная матрица, такая, что [math]HH^=H^H=E[/math] , т.е. [math]H^=H^[/math] . В силу свойства ортогонального преобразования евклидова норма исходной матрицы [math]A[/math] не меняется. Для преобразованной матрицы [math]A^[/math] сохраняется ее след и собственные значения [math]lambda_icolon[/math]

[math]operatorname

A= sum_^a_= sum_^ lambda_i(A)= operatorname

A^.[/math]

При реализации метода вращений преобразование подобия применяется к исходной матрице [math]A[/math] многократно:

Формула (2.6) определяет итерационный процесс, где начальное приближение [math]A^=A[/math] . На k-й итерации для некоторого выбираемого при решении задачи недиагонального элемента [math]a_^,

ine j[/math] , определяется ортогональная матрица [math]H^[/math] , приводящая этот элемент [math]a_^[/math] (а также и [math]a_^[/math] ) к нулю. При этом на каждой итерации в качестве [math]a_^[/math] выбирается наибольший по модулю. Матрица [math]H^[/math] называемая матрицей вращения Якоби, зависит от угла [math]varphi^[/math] и имеет вид

В данной ортогональной матрице элементы на главной диагонали единичные, кроме [math]h_^= cosvarphi^[/math] и [math]h_^=cosvarphi^[/math] , а остальные элементы нулевые, за исключением [math]h_^=-sinvarphi^[/math] , [math]h_^=sinvarphi^[/math] ( [math]h_[/math] -элементы матрицы [math]H[/math] ).

Угол поворота [math]varphi^[/math] определяется по формуле

где [math]|2varphi^|leqslant frac,

i ( [math]a_[/math] выбирается в верхней треугольной наддиагональной части матрицы [math]A[/math] ).

В процессе итераций сумма квадратов всех недиагональных элементов [math]sigms(A^)[/math] при возрастании [math]k[/math] уменьшается, так что [math]sigms(A^) . Однако элементы [math]a_^[/math] приведенные к нулю на k-й итерации, на последующей итерации немного возрастают. При [math]ktoinfty[/math] получается монотонно убывающая ограниченная снизу нулем последовательность sigma(A^)> ldots> sigma(A^)>ldots»>[math]sigma(A^)> sigma(A^)> ldots> sigma(A^)>ldots[/math] . Поэтому [math]sigma(A^)to0[/math] при [math]ktoinfty[/math] . Это и означает сходимость метода. При этом [math]A^to Lambda= operatorname(lambda_1,ldots,lambda_n)[/math] .

Замечание. В двумерном пространстве с введенной в нем системой координат [math]Oxy[/math] с ортонормированным базисом [math]<vec,vec>[/math] матрица вращения легко получается из рис. 2.1, где система координат [math]Ox’y'[/math] повернута на угол [math]varphicolon[/math]

Таким образом, для компонент [math]vec,’,, vec,'[/math] будем иметь [math]bigl(vec,’,vec,’bigr)= bigl(vec,vecbigr)cdot! begin cos varphi&-sin varphi\ sin varphi& cos varphiend[/math] . Отсюда следует, что в двумерном пространстве матрица вращения имеет вид [math]H= begin cos varphi&-sin varphi\ sin varphi& cos varphiend[/math] . Отметим, что при [math]n=2[/math] для решения задачи требуется одна итерация.

Видео:Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Алгоритм метода вращений

1. Положить [math]k=0,

A^=A[/math] и задать 0″>[math]varepsilon>0[/math] .

2. Выделить в верхней треугольной наддиагональной части матрицы [math]A^[/math] максимальный по модулю элемент [math]a_^,

Если [math]|a_^|leqslant varepsilon[/math] для всех [math]ine j[/math] , процесс завершить. Собственные значения определяются по формуле [math]lambda_i(A^)=a_^,

Собственные векторы [math]X^i[/math] находятся как i-e столбцы матрицы, получающейся в результате перемножения:

Если varepsilon»>[math]bigl|a_^bigr|>varepsilon[/math] , процесс продолжается.

3. Найти угол поворота по формуле [math]varphi^= frac operatorname frac<2a_^><a_^-a_^>[/math] .

4. Составить матрицу вращения [math]H^[/math] .

5. Вычислить очередное приближение [math]A^= bigl(H^bigr)^T A^ H^[/math] .Положить [math]k=k+1[/math] и перейти к пункту 2.

1. Используя обозначение [math]overline

_k= frac<2a_^><a_^-a_^>[/math] , можно в пункте 3 алгоритма вычислять элементы матрицы вращения по формулам

2. Контроль правильности выполнения действий по каждому повороту осуществляется путем проверки сохранения следа преобразуемой матрицы.

3. При [math]n=2[/math] для решения задачи требуется одна итерация.

Пример 2.5. Для матрицы [math]A=begin 2&1\1&3 end[/math] методом вращений найти собственные значения и собственные векторы.

1. Положим [math]k=0,

2°. Выше главной диагонали имеется только один элемент [math]a_=a_=1[/math] .

3°. Находим угол поворота матрицы по формуле (2.7), используя в расчетах 11 цифр после запятой в соответствии с заданной точностью:

4°. Сформируем матрицу вращения:

5°. Выполним первую итерацию:

Очевидно, след матрицы с заданной точностью сохраняется, т.е. [math]sum_^a_^= sum_^a_^=5[/math] . Положим [math]k=1[/math] и перейдем к пункту 2.

2. Максимальный по модулю наддиагональный элемент [math]|a_|= 4,!04620781325cdot10^ . Для решения задачи (подчеркнем, что [math]n=2[/math] ) с принятой точностью потребовалась одна итерация, полученную матрицу можно считать диагональной. Найдены следующие собственные значения и собственные векторы:

Пример 2.6. Найти собственные значения и собственные векторы матрицы [math]A=begin5&1&2\ 1&4&1\ 2&1&3 end[/math] .

1. Положим [math]k=0,

2°. Выделим максимальный по модулю элемент в наддиагональнои части: [math]a_^=2[/math] . Так как varepsilon=0,!001″>[math]a_=2> varepsilon=0,!001[/math] , то процесс продолжается.

3°. Находим угол поворота:

4°. Сформируем матрицу вращения: [math]H^= begin0,!85065&0&-0,!52573\ 0&1&0\ 0,!52573&0&0,!85065 end[/math] .

5°. Выполним первую итерацию: [math]A^= bigl(H^bigr)^T A^H^= begin 6,!236&1,!376&2,!33cdot10^\ 1,!376&4&0,!325\ 2,!33cdot10^&0,!325&1,!764 end[/math] . Положим [math]k=1[/math] и перейдем к пункту 2.

2(1). Максимальный по модулю наддиагональный элемент [math]a_^=1,!376[/math] . Так как varepsilon=0,!001″>[math]a_^> varepsilon=0,!001[/math] , процесс продолжается.

3(1). Найдем угол поворота:

4(1). Сформируем матрицу вращения: [math]H^= begin 0,!902937&-0,!429770&0\ 0,!429770&0,!902937&0\ 0&0&1 end[/math] .

5(1). Выполним вторую итерацию: [math]A^= bigl(H^bigr)^T A^H^= begin 6,!891& 2,!238cdot10^&0,!14\ 2,!238cdot10^& 3,!345&0,!293\ 0,!14&0,!293&1,!764 end[/math] . Положим [math]k=2[/math] и перейдем к пункту 2.

2(2). Максимальный по модулю наддиагональный элемент varepsilon=0,!001″>[math]a_^=0,!293> varepsilon=0,!001[/math] .

3(2). Найдем угол поворота:

4(2). Сформируем матрицу вращения [math]H^= begin1&0&0\ 0&0,!9842924& -0,!1765460\ 0& 0,!1765460& 0,!9842924end[/math] .

5(2). Выполним третью итерацию и положим [math]k=3[/math] и перейдем к пункту 2:

2(3). Максимальный по модулю наддиагональный элемент varepsilon»>[math]a_^= 0,!138>varepsilon[/math] .

3(3). Найдем угол поворота:

4(3). Сформируем матрицу вращения: [math]H^= begin 0,!999646&0&-0,!026611\ 0&1&0\ 0,!026611&0&0,!999646 end[/math] .

5(3). Выполним четвертую итерацию и положим [math]k=4[/math] и перейдем к пункту 2:

2(4). Так как varepsilon»>[math]a_^=0,!025>varepsilon[/math] , процесс повторяется

3(4). Найдем угол поворота

4(4). Сформируем матрицу вращения: [math]H^= begin 0,!9999744&-0,!0071483&0\ 0,!0071483&0,!9999744&0\ 0&0&1 end[/math] .

5(4). Выполним пятую итерацию и положим [math]k=5[/math] и перейдем к пункту 2:

2(5). Так как наибольший по модулю наддиагональный элемент удовлетворяет условию [math]bigl|-6,!649cdot10^bigr| , процесс завершается.

Собственные значения: [math]lambda_1cong a_^= 6,!895,,

lambda_3cong a_^=1,!707,,[/math] . Для нахождения собственных векторов вычислим

X^3=begin-0,!473\-0,!171\0,!864 end[/math] или после нормировки

Видео:Крицков Л.В. | Лекция 5 по Алгебре и геометрии | ВМК МГУСкачать

Записная книжка

Компьютерное зрение, машинное обучение, нейронные сети и т.п.

Графы, лапласиан, кластера и т.п.

Графы и всевозможные алгоритмы с ними связанные, раньше входили в тройку лидеров по популярности в разнообразных книжках про программирование, наряду с алгоритмами сортировки и поиска. Теория графов область весьма обширная и пытаться объять её во всей полноте возможных задач в одной статье (или даже в нескольких статьях) совершенно бесполезно, народ пишет серьёзные толстые книжки и при этом тоже далеко не о всех возможных аспектах рассказывает.

Однако, есть желание не особо углублясь во всякого рода хроматические числа, гамильтоновы циклы и прочие познавательные вещи, разобраться с некоторыми базовыми наработками в теории графов и отталкиваясь от них перейти к нейронным сетям на этих графах построенных.

Общие определения

Начнем с формального определения. Граф $mathcal G = (mathcal V, mathcal E)$ есть пара множеств: $mathcal V$ — вершин и $mathcal E$ — рёбер. Вершины обычно обозначаются $mathcal V = $ а рёбра: $mathcal E= <e_= (v_i, v_j)>$. $e_$ — ребро, выходящее из вершины с индексом $i$ и приходящее в вершину с индексом $j$.

Графы бывают ориентированные — когда каждое ребро имеет определенное направление, и неориентированные — когда ребро просто связывает две вершины не упорядоченно или, по другому говоря, если в неориентированном графе есть ребро $e_$, то обязательно присутствует и ребро $e_$.

Для графа с $vert mathcal V vert = N$ вершинами можно задать матрицу смежности $W inmathbb R^$ элемент $w_$ которой характеризует ребро $e_$. В простейшем случае, $w_ = 1$ — если ребро $e_$ есть и $w_ = 0$ — если такого ребра нет. Очевидно, что для неориентированного графа, эта матрица будет симметричной.

Интересная особенность матрицы смежности заключается в том, что в матрице $W^k$ элемент на позиции $(i,j)$ есть число путей длины $k$, которыми можно добраться из вершины $i$ в вершину $j$.

В более общем случае каждому ребру $e_$ можно приписать некоторый вес $w_$ и таким образом получить взвешенный граф.

В дальнейшем мы будем работать с взвешенными неориентированными графами. Если эта пара свойств графа не будет нужна или будет вредна, то это будет оговорено отдельно.

Как в задаче появляются графы?

На самом деле в большинстве случаев граф в задаче появляется вполне естественным образом, например, когда рссматривается дорожная или электрическая сеть, эта сеть уже есть граф. Но иногда граф не задан в явном виде, например, пусть у нас есть набор $x_1, …, x_N$ точек, и для каждой пары точек $x_i, x_j$ задана либо метрика схожести $s_$ либо расстояние $d_$ между точками.

Очевидно, что при построении графа на таких данных в качестве множества вершин берется множество точек $_^N$. Рёбра же можно выбрать несколькими способами, главное, чтобы граф моделировал свойство локальной связи между точками (в [2] описаны три разных способа):

Полный граф. На самом деле самый очевидный способ, это создать полный граф (т.е. у которого есть ребро для каждой пары вершин), задав в качестве веса ребра $w_$ значение метрики схожести $s_$.

Граф по $epsilon$-окрестности. В данном случае соединим ребрами только те вершины расстояние между которыми меньше некоторого наперед заданного $epsilon$. Поскольку $epsilon$ выбирается обычно достаточно малым, то связанные вершины грубо можно считать примерно одинаково близкими поэтому добавление веса на ребро в такой ситуации не добавляет информации, и граф по $epsilon$-окрестности обычно строится невзвешенным.

Граф по $k$-ближайшим соседям. Здесь мы добавляем ребро $e_$, если вершина $v_j$ находится в числе $k$ ближайших соседей к вершине $v_i$. Проблема в том, что при таком подходе мы легко можем получить ориентированный граф, потому что возможна ситуация, когда $v_j$ находится в числе $k$ ближайших к вершине $v_i$, но не наоборот (т.е. $v_i$ не находится в числе $k$ ближайших к вершине $v_j$). Чтобы убрать ориентированность графа есть два варианта.

Первый — просто не учитывать ориентацию ребра, т.е. если $v_j$ находится в числе $k$ ближайших к вершине $v_i$, то в граф мы добавляем и ребро $e_$ и ребро $e_$. Получившийся граф обычно и называют граф по $k$-ближайшим соседям.

Другой вариант, это добавлять пару рёбер $e_$ и $e_$ только если выполены оба условия и $v_j$ находится в числе $k$ ближайших соседей к вершине $v_i$ и $v_i$ в свою очередь находится в числе $k$ ближайших к вершине $v_j$. Полученный таким образом граф называют граф по $k$-ближайшим взаимным соседям.

Лапласиан графа

Введём понятие степень вершины $v_i in mathcal V$:

Для невзвешенного графа это будет просто количество рёбер выходящих из вершины $v_i$, для взвешеного сумма весов таких рёбер. Составим из $d_i$ матрицу степеней (degree matrix):

[D = begin d_ & & 0\ & ddots & \ 0 & & d_ end]

Теперь для графа определим понятие Лапласиана, обычно в литературе встречается три варианта:

1. Ненормализованный Лапласиан.

[mathcal L = D — W]

1. Нормализованный симметричный Лапласиан.

[mathcal L_=D^ mathcal L D^ = I — D^ W D^]

1. Нормализованный несимметричный Лапласиан.

[mathcal L_=D^ mathcal L = I — D^ W]

Замечания.

В первом и втором случаях матрицы очевидно будут симметричными в силу симметричности $W$ и $D$.

Нормализованный симметричный Лапласиан (см., например, [6]) полезен тем, что все его собственные числа не превышают $2$, причем максимум достигается только в случае когда граф двудольный.

Последний вариант Лапласиана тесно связан с матрицей переходов $P = D^ W$ при случайном блуждании (random walk). Случайное блуждание — это алгоритм (применяется для кластеризации, например), когда мы встаём в некоторую начальную вершину и перемещаемся из нее случайным образом, выбирая для перехода ребро пропорционально его весу.

В дальнейшем мы будем пользоваться либо первым либо вторым определением.

Не трудно показать, что для любого вектора $f = (f_1, f_2, …, f_N) in mathbb R^N$ выполняются равенства:

[begin f^T mathcal L f &= frac 1 2 sum_^N w_(f_i — f_j)^2\ f^T mathcal L_ f &= frac 1 2 sum_^N w_left(frac <sqrt > — frac <sqrt >right)^2 end]

А значит и $mathcal L$ и $mathcal L_$ неотрицательно определенные симметричные матрицы.

Лапласиан исходно был обобщением понятия второй производной на случай функции многих переменных (подробно об операторе Лапласа на пространстве функций см., например, [3]).

Пусть $f: mathbb R^N rightarrow mathbb R$, тогда оператор Лапласа определяется как:

Лапласиан как и вторую производную можно рассматривать в некотором смысле как меру гладкости сигнала. А приравняв $Delta f = 0$ мы уйдём в крайне замечательную область математики — гармонический анализ, про который тоже написано много толстых монографий и в который мы углубляться не будем.

Для лапасиана (мы пока остановимся на двух симметричных вариантах, хотя для $mathcal L_$ имеют место примерно теже свойства со скидкой на отсутствие симметрии) можно найти собственные числа и собственные вектора. В силу того, что матрицы симметричны, и неотрицательно определены, у нас будет $lambda_1 le lambda_2 le … le lambda_N$ вещественных собственных чисел. При этом и у $mathcal L$ и у $mathcal L_$ наименьшим собственным числом будет $lambda = 0$ кратность которого совпадает с числом компонент связности графа (доказательство можно найти, например, в [1]) и собственное подпространство соответствующее $lambda = 0$ есть линейная оболочка векторов вида:

где $chi_$ — характеристическая функция компоненты связности $A_i$ (т.е. равна единице на вершинах из данной компоненты связности и нулю на остальных).

Базируясь на этом свойстве лапласиана, строятся алгоритмы кластеризации графа. Мы не будем углубляться в эту весьма познавательную тему, она достаточно подробно раскрывается, например, в [1].

Рассмотрим только один пример для понимания на чем основан подход к кластеризации с использованием лапласиана.

Возьмём граф вида:

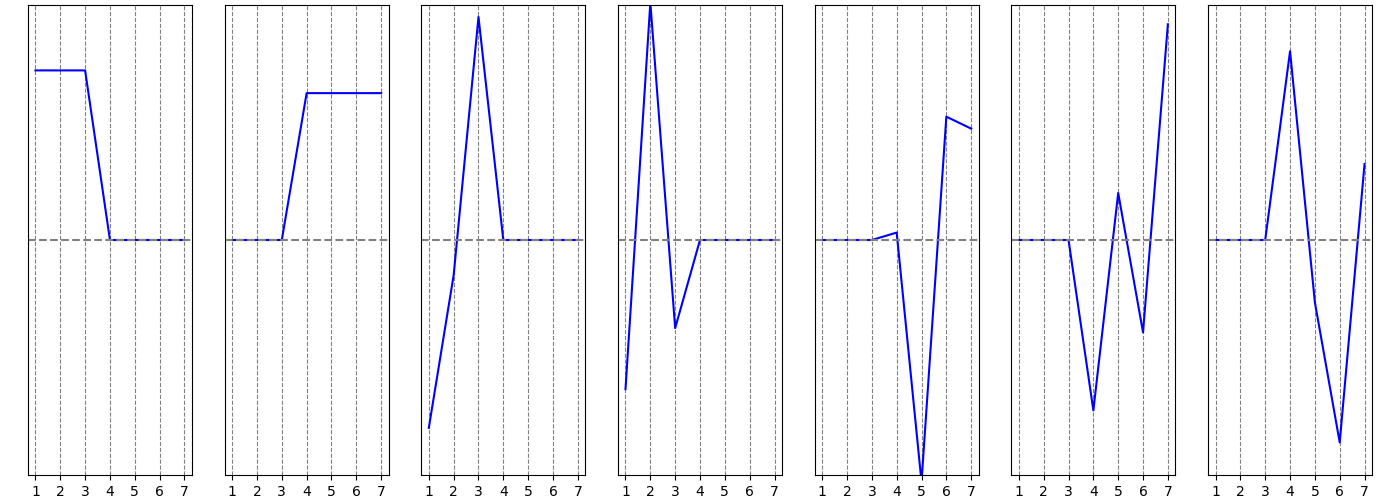
Видно, что он состоит из двух компонент связности. На следующих графиках по вертикальной оси изображены координаты собственных векторов лапласиана (собственные вектора и их графики упорядочены по возрастанию, соответствующих собственных значений):

Первые два графика это собственные вектора, соответствующие собственному числу $lambda = 0$. Видно, что у первого собственного вектора ненулевые координаты соответствуют вершинам $1, 2, 3$, а у второго — $4, 5, 6, 7$. В принципе, этого достаточно для понимания того, что лежит в основе подхода к кластеризации на базе лапласиана. Но если присмотреться к следующим графикам, то на них видно, что второй и третий “разделяют” вершины внутри первого кластера, остальные “разделяют” вершины второго.

Теперь соединим две компоненты связности ребром:

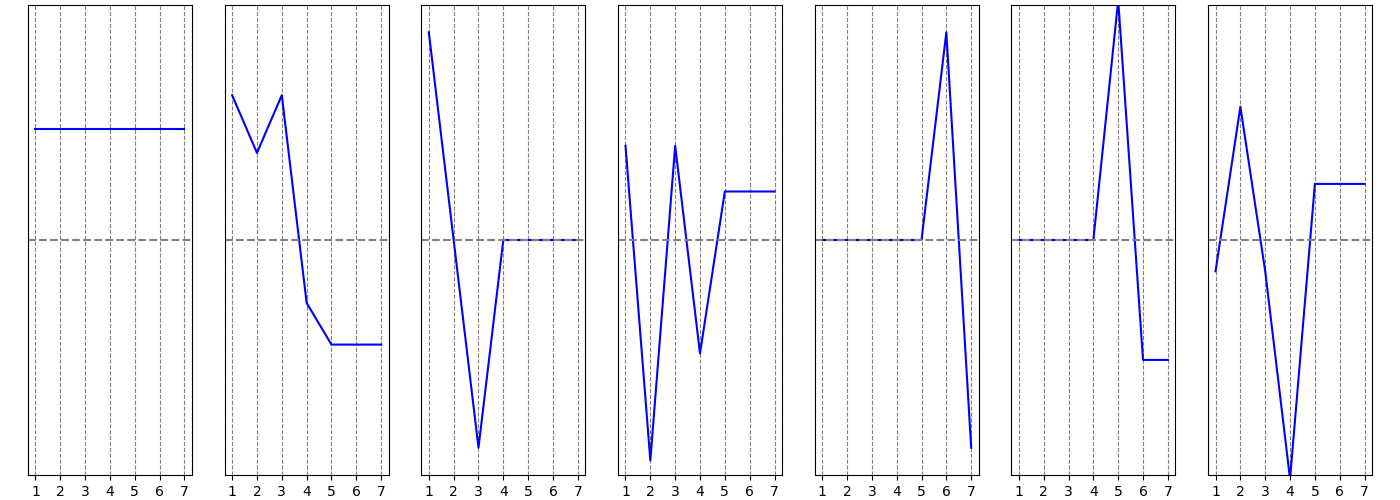
и построем такие же графики координат собственных векторов:

Все координаты первого вектора равны между собой, он соответствует собственному числу $lambda = 0$ (степень этого собственного числа равна 1, что совпадает с числом компонент связности графа $mathcal G_2$). Второй вектор “разделяет” вершины, положительные координаты этого вектора соответствуют вершинам $1, 2, 3$, а отрицательные вершинам $4, 5, 6, 7$. Если продолжать анализ этого вектора, то можно отметить, что абсолютные значения координат для вершин $1$ и $3$ одинаковые и больше абсолютного значения координаты для вершины $2$, аналогично вершина $4$ выделяется относительно вершин $5, 6, 7$, связано это с тем, что именно между вершинами $2$ и $4$ мы добавили ребро, соединяющие две отдельные компоненты, которые были в графе $mathcal G_1$.

Следует отметить еще один факт, который будет нам полезен в дальнейшем. Мы уже отмечали, что если взять $s$-ую степень матрицы смежности (невзвешенной), то элемент $left(W^sright)_$ есть число путей длины $s$, которыми можно добраться из вершины $i$ в вершину $j$. Более слабое утверждение, что

Если из вершины $i$ в вершину $j$ нельзя добраться быстрее чем за $s + 1$ шаг, то $left(W^sright)_ = 0$

Оказывается такое же утверждение можно доказать и для лапласиана графа (см. [4], параграф 5):

Пусть $mathcal G$ — взвешенный граф, $mathcal L$ — его лапласиан (нормализованный или нет) и $s>0$ — целое число, то для любых двух вершин $i$ и $j$, минимальная длина пути между которыми $d_(i, j) > s$ имеем $ left( mathcal L^sright)_ = 0 $

Сигналы на графе, их гладкость и лапласиан

Допустим теперь, что каждой вершине $v_i$ графа приписана некоторая величина $f_i$:

[f: mathcal V rightarrow mathbb R]

или, что тоже самое задан вектор $f = (f_1, f_2, …, f_N) in mathbb R^N$ $i$-ая координата которого определяет значение функции $f$ в $i$-ой вершине графа.

Чтобы показать связь оператора Лапласа на пространстве функций с лапласианом графа, рассмотрим, вначале, дискретный сигнал $ <f_vert m = 1,…,M;, n = 1,…,N>$ на равномерной двумерной решетке с шагом $d$:

В этом случае лапласиан сигнала можно определить представив частные производные в виде разностей (и перейти таким образом для начала от непрерывного случая к дискретному):

Если теперь естественным образом заменить решетку на граф:

положив вес рёбер равным $frac 1 $ получим весовую матрицу:

[W = begin 0 & frac 1 & frac 1 & frac 1 & frac 1 \ frac 1 & 0 & 0 & 0 & 0\ frac 1 & 0 & 0 & 0 & 0\ frac 1 & 0 & 0 & 0 & 0\ frac 1 & 0 & 0 & 0 & 0\ end]

[mathcal L = begin frac 4 & -frac 1 & -frac 1 & -frac 1 & -frac 1 \ -frac 1 & frac 1 & 0 & 0 & 0\ -frac 1 & 0 & frac 1 & 0 & 0\ -frac 1 & 0 & 0 & frac 1 & 0\ -frac 1 & 0 & 0 & 0 & frac 1 \ end]

Т.е. в случае равномерной решётки, воздействие лапласиана $mathcal L$ графа, соответствующего этой решётке, на сигнал $f$ в вершинах графа равен лапласиану (с обратным знаком правда) функции $f$.

Для сигнала $f$, заданного на графе $mathcal G = (mathcal V, mathcal E)$ определим производную сигнала $f$ по ребру $e_$ в вершине $v_$:

учтя это, можно определить градиент сигнала $f$ в вершине $v_$:

локальную вариацию в вершине $v_$ можно записать как норму градиента в этой вершине:

Эту норму можно рассматривать как характеристику локальной гладкости сигнала $f$ в вершине $v_i$ (суммирование идёт по всем $j$, т.е. по всем вершинам графа, но за счёт весов, в суммирование учавствуют только “соседние” к $v_i$ вершины), эта величина мала, если значение функционала в $i$-ой вершине мало отличается от значений функционала в соседних вершинах (связанных рёбрами с $v_i$).

Если теперь рассмотреть вектор

[nabla_ f = left(left | nabla_ f right |_2, left | nabla_ f right |_2, . left | nabla_ f right |_2 right)]

то его норма будет глобальной вариацией сигнала на графе:

[left | nabla_ f right |_2 = left(sum_^N w_ (f_j — f_i)^2right)^ = left( 2 f^T mathcal L f right)^]

Т.о. лапласиана вбирает в себя структурные свойства графа, и в некотором смысле может показать “согласованность” сигнала со структурой графа.

Рассмотрим в качестве примера один и тот же сигнал $f = (0, 1, 2, 2, 2, -1, -2, -2, -2)$, на трёх разных графах отличающихся только конфигурацией рёбер (пример взят из [2], во всяком случае идейно):

Очевидно, что сигнал наиболее согласован со структурой графа $mathcal G_1$, на втором эта согласованность уменьшается за счёт появления рёбер между вершинами в которых значение сигнала сильно отличается, на третьем графе эта рассогласованность ещё больше усиливается.

А теперь сравним величину $f^T mathcal L f$ на всех трёх графах:

Действительно, наша интуитивная оценка согласованности сигнала со структурой графа, подтвердилась.

Преобразование Фурье

В функциональном анализе с лапласианом, тесно связано понятие преобразования Фурье.

Преобразованием Фурье абсолютно интегрируемой функции $f in mathcal L_1(-infty, infty)$ называется функция $tilde f$ определенная формулой:

восстанавливает исходную функцию по её преобразованию Фурье (про возможность такой процедуры и в каком смысле рассматривается интеграл в правой части последней формулы можно посмотреть, например, в [5])

Связь с оператором Лапласа, заключается в том, что экспоненты $e^$ суть его собственные вектора. Действительно

У графа мы тоже научились находить лапласиан и даже показали схожесть лапласиана на графе и лапласиана на пространстве функций. Теперь, воспользуемся лапласианом, чтобы определить преобразование Фурье.

Для лапласиана $mathcal L$ мы можем найти собственные числа $0=lambda_1 le lambda_2 le … le lambda_N$ и собственные вектора:

Собственные вектора выберем таким образом, чтобы они составляли ортонормированный базис пространства $mathbb R^N$. Если из этих векторов составить матрицу $U = (u^, u^,…, u^)$ (вектора — столбцы матрицы), то эта матрица будет ортогональной, т.е. $U U^T = U^T U = I$.

А еще можно записать разложение: $mathcal L=U Lambda U^T$, где $Lambda = mathrm(lambda)$ — диагональная матрица, составленная из собственных чисел лапласиана.

Теперь определим преобразование Фурье на графе сигнала $f = (f_1, f_2, …, f_N)^T in mathbb R^N$ как сигнал:

[tilde f = U^T f = (tilde f_1, tilde f_2, . tilde f_N)^T]

не трудно видеть, что $i$-ая координата преобразования Фурье определяется формулой (скалярное произведение векторов $u^$ и $f$):

[tilde f_i = sum_^N u^_j f_j,, i = 1, . N]

Поскольку $U$ ортогональная матрица, то очевидно имеет место и обратное преобразование:

[U tilde f = U cdot left(U^T fright) = I f = f]

С преобразованием Фурье тесно связаны понятия спектра и частот. В данном случае в качестве частот у нас выступают собственные числа лапласиана графа. Определив преобразование Фурье на графе, мы можем применять к сигналам заданным на этом графе фильтры не только непосредственно (например, заменяя сигнал в вершине графа на взвешенное среднее по сигналу в соседних к данной вершинах), но и в частотной области, например, удаляя из сигнала высокие частоты (т.е. зануляя коэффициенты Фурье $tilde f_i$, соответствующие большим $lambda_i$).

Здесь надо заметить, что для картинок (сигнала на двумерной решётке), процесс “удаления из сигнала высоких частот” тесно связан с очисткой от зашумленности.

Произвольный фильтр в частотной области можно определить как вектор: $tildetheta = left(tildetheta_1, tildetheta_2,…, tildetheta_Nright)$, его применение будет выглядеть как поэлементное произведение вектора $tilde theta$ на вектор $tilde f$:

[tilde g = tilde theta odot tilde f]

или, если сделать из вектора $tilde theta$ диагональную матрицу, то поэлементное умножение, заменится умножением матрицы на вектор:

[tilde g = mathrm(tilde theta) tilde f]

Используем обратное преобразование Фурье и тогда полное применение фильтра $tilde theta$ на графе $mathcal G$ к сигналу $f$ можно записать в виде:

[g = U cdot mathrm(tilde theta) cdot U^T f]

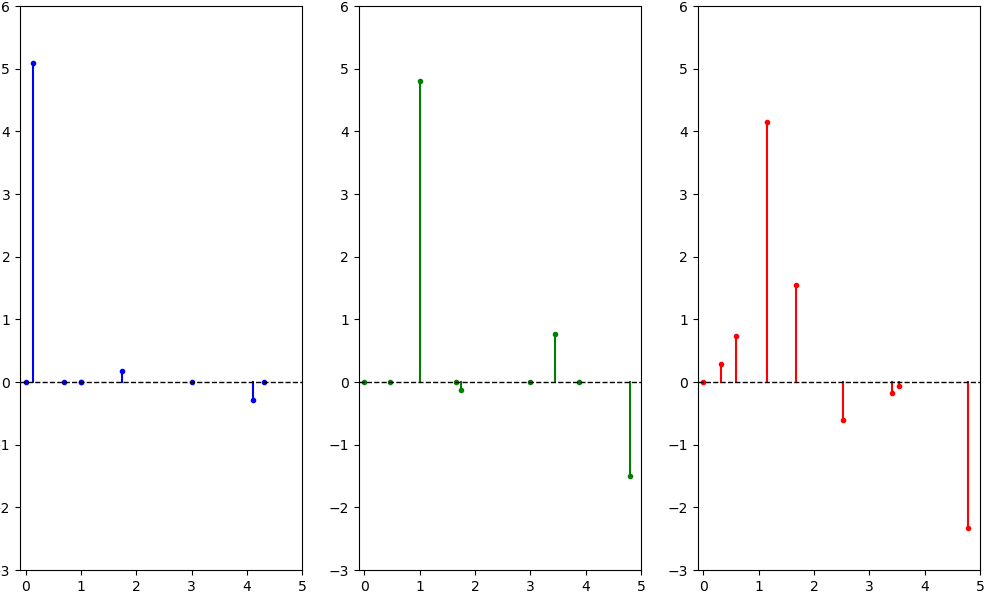
Вернемся к примеру сигнала $f = (0, 1, 2, 2, 2, -1, -2, -2, -2)$ на трёх разных графах:

посчитаем преобразование Фурье, и отложим по горизонтальной оси частоты (собственные числа лапласиана), а по вертикальной значение коэффициентов Фурье для соответствующих частот:

Теперь оставим только низкие частоты, используя в качестве $tilde theta = left(1, 1, 1, 0, 0, 0, 0, 0, 0right)$ (занулим у преобразования Фурье сигналов, все координаты кроме первых трёх). Отфильтровав таким образом высокие частоты, и сделав обратное преобразование Фурье получим новые сигналы на графах:

На изображении значение сигналов округлено до десятых.

Если двигаться по рёбрам, видно, что отбрасывание высоких частот действительно в некотором смысле “сгладило” сигнал.

Свёртка сигналов на графе

Мы можем рассмотреть $tilde theta$ из предыдущего пункта, как преобразование Фурье некоторого сигнала $theta$ на графе, и восстановить этот сигнал очевидным образом:

[theta = U tilde theta]

А теперь вспомним одну из основных теорем связанных с преобразованием Фурье — теорему о свёртке.

Пусть у нас $f_1$ и $f_2$ интегрируемые на всей действительной оси функции, тогда их свёрткой $f_1 ast f_2$ называется функция:

При этом преобразование Фурье $F$ свёртки есть произведение преобразований Фурье двух исходных функций, т.е.:

[F(f_1 ast f_2) = F(f_1)F(f_2)]

По аналогии с “теоремой о свёртке”, преобразование $ast_$, задаваемое формулой:

[f ast_ theta = U cdot left((U^T theta) odot (U^T f) right)]

мы будем называть свёрткой сигналов $theta$ и $f$ на графе $mathcal G$.

Однако, для практических целей нам интересны свёртки с такими сигналами, аналогами которых в пространстве функций будут финитные функции или, что тоже самое, функции с ограниченным носителем. Т.е. нам желательно, чтобы результат свёртки для вершины формировался на основе сигнала в соседних вершинах. А для этого предлагается представить преобразование Фурье фильтрующего сигнала в виде:

[tilde theta = left(h(lambda_1), h(lambda_2), . h(lambda_N)right)]

[h(lambda) = sum_^K a_k lambda^k]

многочлен степени $K$, и для получения координаты $tilde theta_i$ мы считаем значение этого многочлена от собственного числа $lambda_i$. В этом случае:

[begin g &= U cdot begin h(lambda_1) & & 0\ & ddots & \ 0 & & h(lambda_N) end cdot U^T f =\ \ &= U cdot left[ a_0 cdot I + a_1 cdot begin lambda_1 & & 0\ & ddots & \ 0 & & lambda_N end + . +a_K cdot begin lambda_1^K & & 0\ & ddots & \ 0 & & lambda_N^K end right]cdot U^T f =\ \ &= U cdot left[ a_0cdot I + a_1 cdot Lambda +. +a_K cdot Lambda^Kright]cdot U^T f =\ \ &= left(a_0 cdot U cdot I cdot U^T + a_1 cdot U cdot Lambda cdot U^T +. +a_K cdot U cdot Lambda^K cdot U^Tright) f end]

так как $U^T U = I$ и $U Lambda U^T = mathcal L$, заменим

[U Lambda^k U^T = U Lambda U^T U Lambda . U^T U Lambda U^T = mathcal L^k]

[begin g &= left(a_0 cdot I + a_1 cdot mathcal L + . + a_K cdot mathcal L^K right) f \ &= a_0 cdot f + a_1 cdot mathcal L cdot f + . + a_K cdot mathcal L^K cdot f end]

а значит, обозначая $left(mathcal L^kright)_$ элемент матрицы $mathcal L^k$, стоящий на позиции $i,j$, и полагая, по определению $mathcal L^0 = I$, можно для того, чтобы получить координаты сигнала $g$, использовать формулу:

[begin g_i &= a_0 f_i + a_1 sum_^N (mathcal L)_ f_j + . + a_K sum_^N left(mathcal L^Kright)_ f_j = \ &= sum_^K a_k sum_^N f_j left(mathcal L^kright)_ = sum_^N f_j sum_^K a_k left(mathcal L^kright)_ end]

А теперь вспомним свойство степеней лапласиана, а именно $left(mathcal L^kright)_ = 0$, в случае если кратчайший путь между вершинами $i$ и $j$ содержит больше $k$ рёбер. Таким образом, если мы определяем наш свёрточный фильтр в частотной области при помощи многочлена степени $K$ (от собственных чисел лапласиана), то после фильтрации мы получим новый сигнал, который в данной вершине будет линейной комбинацией от сигнала в вершинах отстающих от данной не более чем на $K$ шагов. В каком то смысле мы таким образом получаем свёртку исходного сигнала с сигналом с компактным носителем.

Литература

Ulrike von Luxburg. “A Tutorial on Spectral Clustering”, arXiv:0711.0189, 2007

D. I. Shuman, S. K. Narang, P. frossard, A. Ortega, P. Vandergheynst, “The Emerging field of Signal Processing on Graphs: Extending High-Dimensional Data Analysis to Networks and Other Irregular Domains”, arXiv:1211.0053, 2013

Тиман А. Ф., Трофимов В. Н. “Введение в теорию гармонических функций”, М., 1968 г.

D. K. Hammond, P. Vandergheynstb, R. Gribonval, “Wavelets on Graphs via Spectral Graph Theory”, arXiv:0912.3848, 2009

Колмогоров А. Н., Фомин С. В. “Элементы теории функций и функционального анализа”, М., 1976 г.

F. K. Chung, “Spectral Graph Theory”, 1997