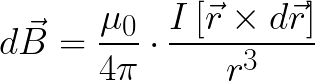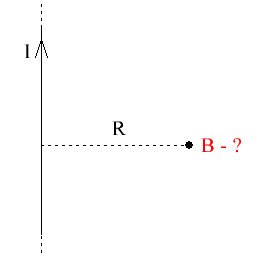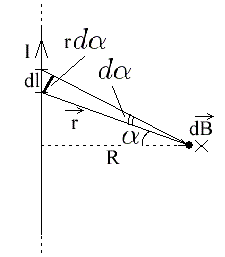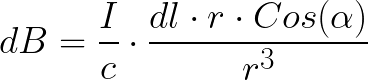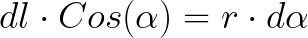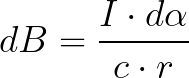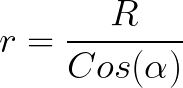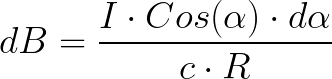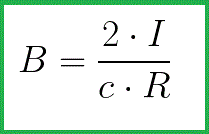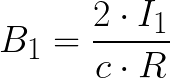6.5. Взаимодействие двух проводников с током

Применим закон Ампера для вычисления силы взаимодействия двух длинных прямолинейных проводников с токами I₁ и I₂, находящихся на расстоянии d друг от друга (рис. 6.26).

Рис. 6.26. Силовое взаимодействие прямолинейных токов:
1 — параллельные токи; 2 — антипараллельные токи

Проводник с током I₁ создает кольцевое магнитное поле, величина которого в месте нахождения второго проводника равна

Это поле направлено «от нас» ортогонально плоскости рисунка. Элемент второго проводника испытывает со стороны этого поля действие силы Ампера

Подставляя (6.23) в (6.24), получим

При параллельных токах сила F₂₁ направлена к первому проводнику (притяжение), при антипараллельных — в обратную сторону (отталкивание).

Аналогично на элемент проводника 1 действует магнитное поле, создаваемое проводником с током I₂ в точке пространства с элементом с силой F₁₂. Рассуждая таким же образом, находим, что F₁₂ = –F₂₁, то есть в этом случае выполняется третий закон Ньютона.

Итак, сила взаимодействия двух прямолинейных бесконечно длинных параллельных проводников, рассчитанная на элемент длины проводника, пропорциональна произведению сил токов I₁ и I₂ протекающих в этих проводниках, и обратно пропорциональна расстоянию между ними. В электростатике по аналогичному закону взаимодействуют две длинные заряженные нити.

На рис. 6.27 представлен опыт, демонстрирующий притяжение параллельных токов и отталкивание антипараллельных. Для этого используются две алюминиевые ленты, подвешенные вертикально рядом друг с другом в слабо натянутом состоянии. При пропускании через них параллельных постоянных токов силой около 10 А ленты притягиваются. а при изменении направления одного из токов на противоположное — отталкиваются.

Рис. 6.27. Силовое взаимодействие длинных прямолинейных проводников с током

На основании формулы (6.25) устанавливается единица силы тока — ампер, являющаяся одной из основных единиц в СИ.

Ампер — это сила неизменяюшегося тока, который, протекая по двум длинным параллельным проводникам, расположенным в вакууме на расстоянии 1 м, вызывает между ними силу взаимодействия 2×10 –7 Н на каждый метр длины провода.

Пример. По двум тонким проводам, изогнутым в виде одинаковых колец радиусом R = 10 см, текут одинаковые токи I = 10 А в каждом. Плоскости колец параллельны, а центры лежат на ортогональной к ним прямой. Расстояние между центрами равно d = 1 мм. Найти силы взаимодействия колец.

Решение. В этой задаче не должно смущать, что мы знаем лишь закон взаимодействия длинных прямолинейных проводников. Поскольку расстояние между кольцами много меньше их радиуса, взаимодействующие элементы колец «не замечают» их кривизны. Поэтому сила взаимодействия дается выражением (6.25), куда вместо надо подставить длину окружности колец Получаем тогда

Содержание

Объясняем закон Ампера простым языком
Общее представление об электромагнитном поле
Формулировка закона Ампера
Взаимодействие тока и магнитного поля
Направление электромагнитной силы
Влияние замкнутого контура
Использование бесконечно малых величин
Практическое применение
Видео по теме
Взаимодействие параллельных проводников с током (параллельных токов)
📸 Видео

Видео:Взаимодействие параллельных токовСкачать

Объясняем закон Ампера простым языком

Проводник, по которому течёт электрический ток, взаимодействует с существующими магнитными полями. На этом основана работа многих электротехнических устройств. Закон Ампера позволяет рассчитать такие взаимодействия. Он стал основой многих открытий в физике и часто применяется в современной технике. А имя Андре-Мари Ампера увековечено наряду с именами других 72 величайших ученых в списке, помещенном на первом этаже Эйфелевой башни.

Видео:Взаимодействие токовСкачать

Общее представление об электромагнитном поле

Длительное время представления об электрическом и магнитном поле не связывались между собой. Практические эксперименты подтверждали, что каждое из них имеет свои особенные свойства. Исследования Фарадея и Максвелла показали, что существует электромагнитное поле, которое может проявлять себя как электрическое или магнитное. Его можно описать с мощью вектора напряжённости. Если знать величину и направление данного вектора, то можно рассчитать силу воздействия.

Первым из учёных, кто обратил внимание на взаимное влияние магнитного поля и тока был известный учёный Х. К. Эрстед. Он исследовал влияние проводника с текущим по нему током на положение стрелки компаса. После этого учёные стали систематически изучать различные варианты взаимодействия.

Ампер появился на свет в 1775 году в Лионе. С детства он проявлял страсть к математике. Будучи подростком, изучал труды Эйлера и Лагранжа. Профессором математики Ампер стал в 1809 году, а в 1814 году был избран в академию наук. Хотя он преимущественно занимался математикой, его интересовала физика и некоторые другие науки.

Ампер был не первым человеком, который проявил интерес к связи магнитных и электрических полей, однако он впервые постарался найти точное математическое описание происходящих процессов. Им был не только установлен факт взаимодействия между электрическими токами, но и сформулирован закон данного явления.

Ампер доказал, что проводники начинают взаимодействовать, если по каждому из них протекает ток. В этом случае между ними возникают силы отталкивания или притягивания. В 1826 году Ампер впервые опубликовал результаты своего исследования, с помощью которого он изучал взаимодействие параллельных токов.

На рисунке ниже представлена схема одного из экспериментов Ампера, с помощью которого измеряется сила, действующая на проводник с током в магнитном поле. Стрелка красного цвета на рисунке показывает направление тока.

Основываясь на экспериментах, учёный сделал предположение, которое впоследствии получило название «гипотеза Ампера». Понимая, как влияет ток на магнитное поле, он сумел доказать, что вещество состоит из совокупности чрезвычайно маленьких круговых токов. Каждый из них порождает очень слабое магнитное поле. Поскольку все эти токи ориентированы хаотично, то внешне магнитное поле практически не проявляется. Однако в магнитах все круговые токи одинаково направлены и их воздействие складывается. Этим объясняются их особые свойства и практическое использование.

Ампер, используя свой закон, также объяснил эффект намагничивания. Согласно ему, у некоторых веществ под воздействием магнитного поля происходит упорядочивание круговых токов, и они постепенно ориентируются в одну сторону.

Эта гипотеза стала одним из источников теории магнетизма. Она смогла объяснить явление только частично, так как не дала ответа на вопрос о том, почему некоторые вещества подвергаются воздействию внешнего магнитного поля незначительно. Также остался необъяснённым вопрос, почему при намагничивании одни вещества создают магнитный поток сонаправленный внешнему полю (парамагнетики), а другие — противоположно направленный (диамагнетики).

Видео:Магнитное поле между двумя проводниками с током.Часть 1 (видео 9) | Магнетизм | ФизикаСкачать

Формулировка закона Ампера

При исследовании параллельных проводников с током было выяснено, что между ними действует сила притяжения, если токи однонаправленные, и отталкивания, если токи противоположно направленные. Сила взаимодействия токов зависит пропорционально от произведения сил токов и длины проводника. Справедливо также утверждение, что она обратно пропорциональна имеющемуся между проводами расстоянию. Математическая формулировка выглядит следующим образом:

Закон Ампера в такой формулировке показывает, что расчет силы магнитного поля производится по отношению к единице длины проводника. Силу, которую проводник с током испытывает в магнитном поле, называют силой Ампера.

Взаимодействие токов возможно лишь при наличии магнитных полей вокруг проводников. Эти поля создают движущиеся заряды. У магнитов постоянных магнитное поле, как утверждает закон Ампера, тоже возникает под воздействием электрических микротоков, но только тех, которые циркулируют внутри молекул вещества.

При описании магнитного поля принято использовать силовую характеристику, аналогичную вектору напряженности электрополя. Ее называют вектором магнитной индукции и обозначают латинской буквой «B». В системе СИ за единицу измерения данной характеристики принята Тесла: 1 Тл = 1 Н/А×м.

Направление вектора МИ определяется по правилу буравчика. Если штопор направить перпендикулярно плоскости проводника с током, то движение краёв рукоятки укажет направление вектора напряжённости. Подразумевается, что рукоятка будет вращаться по ходу часовой стрелки, если наблюдать сзади.

Видео:Опыты по физике. Взаимодействие параллельных токовСкачать

Взаимодействие тока и магнитного поля

Вектор магнитной индукции считается положительно направленным, если он совпадает с магнитной стрелкой, ориентированной на северный полюс. Используя это правило, можно определить направление вектора МИ в любой точке пространства и наглядно представить структуру магнитного поля. На рисунке ниже приведен пример расположения линий МИ для постоянного магнита и катушки с током.

Ампер смог рассчитать, как будет проходить взаимодействие между магнитным полем с заданной напряжённостью и проводником, по которому течёт ток. Согласно его закону действие магнитного поля на проводник с током описывается с помощью такой формулы:

Данная формула представлена в векторной форме. Умножение между векторами производится по особым правилам. В результате этой операции получится вектор, абсолютная величина которого определяется по следующей дифференциальной формуле:

Для прямолинейного провода данная формула в скалярной форме имеет вид:

Хотя, кажется, что закон достаточно прост, он стал важным достижением в развитии физической науки.

Видео:Взаимодействие двух параллельных токовСкачать

Направление электромагнитной силы

Если взять проводник с током и расположить его между полюсами магнита, как показано на рисунке ниже, то сила Ампера находится по формуле:

F = B × L × I, поскольку α = 90 градусов и sinα = 1.

Определение вектора действия силы выполняется согласно правилу левой руки. В этом случае нужно расположить ладонь левой руки перпендикулярно к силовым линиям магнитного поля. Пальцы при этом должны быть направлены в ту сторону, в которую течет ток. В таком положении перпендикулярно отставленный большой палец будет показывать направление электромагнитной силы.

При определении вектора силы, действующей на проводник, нужно учитывать, что ток всегда направлен от плюса к минусу. Это сложилось исторически, а потом стало традицией, несмотря на то, что в проводниках ток представляет собой движение электронов, то есть, отрицательных частиц.

В рассматриваемой ситуации можно регулировать силу взаимодействия, увеличивая или уменьшая силу тока. При этом напряжённость магнитного поля остается неизменной.

Проиллюстрировать применение правила левой руки можно на простом примере. Как уже было сказано выше, параллельные проводники с однонаправленными токами притягиваются. Правило поможет разобраться, почему это происходит.

Вокруг каждого проводника, по которому протекает ток, возникает магнитное поле. Нужно определить, как будет направлен вектор его напряжённости. Если взгляд направить вдоль проводника, то линии магнитной индукции поля будут видны в виде окружностей. Другими словами, если мысленно обхватить проводник правой рукой, направив большой палец по течению тока, то остальные четыре пальца будут соответствовать линиям напряженности магнитного поля.

Помещая первый проводник параллельно второму проводнику в магнитное поле, созданное последним, можно определить направление электромагнитной силы, используя правило левой руки. Расположив ее таким образом, чтобы получить линии МИ, входящие в ладонь, а направление пальцев, совпадающее с направлением тока, можно увидеть, что отогнутый большой палец указывает на второй проводник.

Понятно, что данное правило одинаково относится к обоим проводникам. Следовательно, можно определить направление электромагнитной силы в различных ситуациях. Аналогично можно видеть, что при противоположном направлении токов, действует сила отталкивания.

Видео:Взаимодействие параллельных токовСкачать

Влияние замкнутого контура

Используя закон Ампера можно сделать вывод о том, каким будет магнитное поле замкнутого контура. Например, можно вертикально ориентировать рамку в поле, силовые линии которого направлены сверху вниз.

Чтобы определить, какое направление будет иметь магнитная индукция в этой ситуации, следует также воспользоваться правилом левой руки. Так как ток в нижней части рамки направлен вправо, руку нужно расположить так, чтобы пальцы были направлены, если смотреть на рисунок, тоже вправо. При этом ладонь должна быть открыта вверх. Большой палец в такой ситуации будет направлен в сторону от наблюдателя.

Применив это правило для верхней части рамки, можно увидеть, что сила Ампера действует по направлению к наблюдателю. То есть, рамке придано вращательное движение. Однако по мере приближения к горизонтальному положению эта сила уменьшается.

Если рамка будет обладать инерцией и благодаря ей проскочит горизонтальное положение, то описанные выше силы вновь начнут действовать: вначале слабо, а затем будут увеличиваться по мере достижения рамкой вертикального положения.

Видео:Взаимодействие параллельных токовСкачать

Использование бесконечно малых величин

В указанных выше формулах применяются бесконечно малые величины (dF, dl). Их использование расширяет возможности расчёта параметров. Обычно экспериментально исследуются сравнительно простые ситуации, но при этом возникает необходимость получить формулы универсального характера.

В реальной жизни возможны, например, ситуации, когда напряжённость магнитного поля меняется по сложному закону или рассматриваются контуры проводников произвольной конфигурации.

Использование бесконечно малых величин даёт возможность обобщить результаты основополагающих экспериментов для самых разных ситуаций. Для этого могут быть применены методы дифференциального и интегрального исчисления.

При рассмотрении бесконечно малого участка провода речь идёт о величине, которая достаточно мала, чтобы считать её прямолинейной. В этом случае возможно применение уже существующих закономерностей. При помощи методов интегрирования можно перейти к проводам, которые имеют контур различной степени сложности или к рассмотрению магнитного поля сложной конфигурации.

Видео:Взаимодействие параллельных токов.Скачать

Практическое применение

Сила Ампера используется практически во всех электромеханических устройствах, где необходимо с помощью электрических процессов вызвать движение реальных объектов. Одним из примеров применения являются измерительные приборы.

На рисунке приведен пример схемы измерительного прибора. К оси присоединен источник питания (4). Ось закреплена в подшипниках (5), поэтому может свободно вращаться. На оси есть прямоугольная рамка (1), через которую течёт ток. Она расположена между полюсами постоянного магнита (2). Контакты сделаны в виде спиральных пружин. К оси прикреплена стрелка (6), острие которой передвигается по шкале измерения (7).

При пропускании тока через проводник появляется магнитное взаимодействие, и рамка начинает вращаться. При этом смещается стрелка указателя до тех пор, пока сила Ампера не уравновесит силу упругости обеих пружин. Полученный показатель будет характеризовать ток, протекающий через проводник. Чем больше сила тока, тем сильнее отклонится стрелка.

На законе Ампера основывается и такая отрасль, как электротехника. Например, электромагнитная индукция применяется в электродвигателях.

Двигатель обеспечивает преобразование электроэнергии во вращение вала. Ток на рамку поступает через скользящие щётки. Она взаимодействует с постоянным магнитом, что приводит к её повороту под действием силы Ампера. В современных двигателях может использоваться одновременно несколько рамок. Это позволяет увеличить мощность мотора и сделать вращение оси более плавным.

Двигатели, работающие на основе рассматриваемого эффекта, активно используются в различных видах электротранспорта — трамваях, троллейбусах, электропоездах.

Еще одно применение закона Ампера — это громкоговорители. Внутри них находится постоянный магнит. Изменение силы тока вызывает изменение силы воздействия магнитного поля, что приводит к вибрации мембраны, производящей звук нужной частоты.

Притяжение между проводниками с током легло в основу точного определения единицы измерения 1 Ампер. При этом рассматривалась абстрактная ситуация, предполагающая наличие двух параллельно расположенных проводников с бесконечной длиной. Считалось, что каждый из них имеет бесконечно малое сечение, размерами которого можно пренебречь.

Принято, что на всём протяжении они находятся точно на расстоянии один метр и в вакууме. При прохождении тока величиной 1 Ампер сила, действующая на каждый метр проводников, должна составлять 0.0000002 Ньютона. Это определение вступило в силу в 1948 году.

Видео:Взаимодействие параллельных проводников с током. Физика -9 й класс.Скачать

Видео по теме

Взаимодействие параллельных проводников с током (параллельных токов)

Определить в некоторой точке пространства вектор индукции магнитного поля B, порождаемого постоянным электрическим током I, можно с помощью Закона Био-Савара. Это делается путем суммирования всех вкладов в магнитное поле от отдельных элементов тока.

Магнитное поле элемента тока dI, в точке, заданной вектором r, по Закону Био-Савара находится так (в системе СИ):

Одна из типичных задач состоит в том, чтобы далее определить силу взаимодействия двух параллельных токов. Ведь токи, как известно, порождают собственные магнитные поля, а ток, находящийся в магнитном поле (другого тока) испытывает на себе действие силы Ампера.

Под действием силы Ампера, противоположно направленные токи взаимно отталкиваются, а токи направленные в одну сторону — взаимно притягиваются.

Прежде всего для прямого тока I нам необходимо найти магнитное поле B на некотором расстоянии R от него.

Для этого вводится элемент длины тока dl (по направлению тока), и рассматривается вклад от тока в месте расположения данного элемента длины — в общую индукцию магнитного поля применительно к выбранной точке пространства.

Сначала будем записывать выражения в системе СГС, то есть появится коэффициент 1/с, а в конце приведем запись в системе СИ, где появится магнитная постоянная.

По правилу нахождения векторного произведения, вектор dB — результат векторного произведения dl на r для любого элемента dl, в каком бы месте рассматриваемого проводника он не находился, всегда будет направлен за плоскость рисунка. Результат будет равен:

Произведение косинуса на dl можно выразить через r и угол:

Значит выражение для dB примет вид:

Далее выразим r через R и косинус угла:

И выражение для dB примет вид:

Далее необходимо это выражение проинтегрировать в пределах от -пи/2 до +пи/2, и в результате получим для B в точке на расстоянии R от тока следующее выражение:

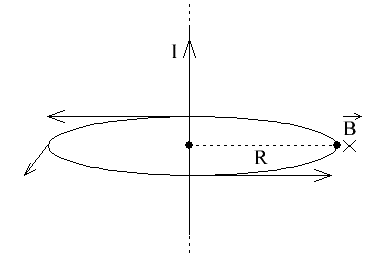
Можно сказать, что вектор B найденной величины, для выбранной окружности радиуса R, через центр которой перпендикулярно проходит данный ток I, всегда будет направлен по касательной к данной окружности, какую бы точку окружности мы ни выбрали. Здесь присутствует осевая симметрия, так что вектор B в любой точке окружности получается одной и той же длины.

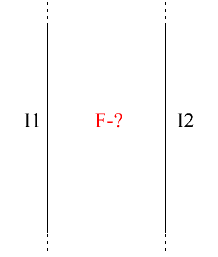
Теперь рассмотрим параллельные постоянные токи и решим задачу нахождения сил их взаимодействия. Допустим, что параллельные токи направлены в одну и ту же сторону.

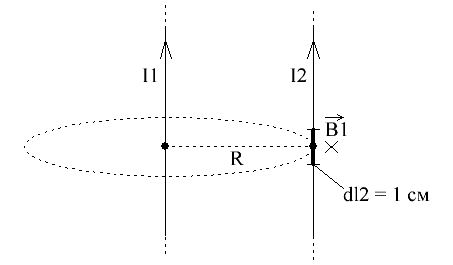
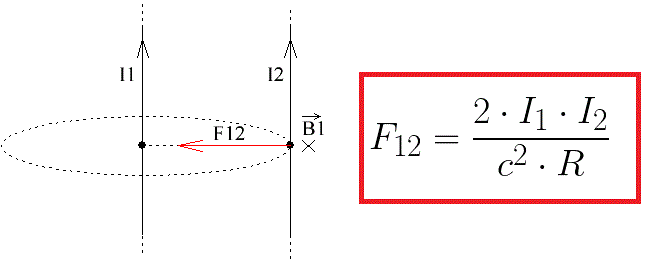
Изобразим магнитную силовую линию в форме окружности радиуса R (о которой речь шла выше). И пусть второй проводник расположен параллельно первому в какой-то точке данной силовой линии, то есть в месте с индукцией, значение которой (в зависимости от R) мы только что научились находить.

Магнитное поле в этом месте направлено за плоскость рисунка, и оно действует на ток I2. Выделим элемент длины тока l2, равный одному сантиметру (единица длины в системе СГС). Далее рассмотрим силы, действующие на него. Будем использовать Закон Ампера. Индукцию в месте расположения элемента длины dl2 тока I2 мы нашли выше, она равна:

Следовательно сила, действующая со стороны всего тока I1 на единицу длины тока I2 будет равна:

Это и есть сила взаимодействия двух параллельных токов. Поскольку токи однонаправленные и они притягиваются, то сила F12 со стороны тока I1 направлена так, что она тянет ток I2 в сторону тока I1. Со стороны же тока I2 на единицу длины тока I1 действует сила F21 равной величины, но направленная в сторону противоположную силе F12, в соответствии с третьим законом Ньютона.

В системе СИ, сила взаимодействия двух постоянных параллельных токов находится по следующей формуле, где коэффициент пропорциональности включает в себя магнитную постоянную: