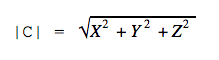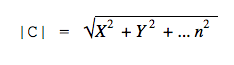Сложить вектора ab ac

Теорема 1 От любой точки ( K ) можно отложить вектор единственный ( overrightarrow ) .

Существование: Имеем два следующих случая:

Здесь получаем, что искомый нами вектор совпадает с вектором ( overrightarrow ) .

Из данного выше построения сразу же будет следовать единственность данного вектора.

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Сумма векторов. Сложение векторов. Правило треугольника

Сложение векторов выполняется по правилу треугольника или по правилу параллелограмма.

Суммой нескольких векторов ( vec ) , ( vec ) , ( vec,;ldots ) называется вектор ( vec ) , получающийся в результате последовательного сложения данных векторов.

Такая операция выполняется по правилу многоугольника.

Сумма векторов в координатах
При сложении двух векторов соответствующие координаты складываются.
( vec + vec = left( <+ , + , + > right) )

Отметим несколько свойств сложения двух векторов:

Для произвольного вектора ( overrightarrow ) выполняется равенство

Для произвольных точек ( A, B и C ) справедливо следующее равенство

Замечание Таким способом также можно строить сумму любого числа векторов. Тогда оно будет носить название правила многоугольника.

Видео:Вычитание векторов. 9 класс.Скачать

Разность векторов. Вычитание векторов

Разность двух одинаковых векторов равна нулевому вектору :
( vec — vec = vec )

Длина нулевого вектора равна нулю:
( left| vec right| = 0 )

Разность векторов в координатах
При вычитании двух векторов соответствующие координаты также вычитаются.
( vec — vec = left( <- , — , — > right) )

Видео:ВЫЧИТАНИЕ ВЕКТОРОВ ЧАСТЬ I #егэ #огэ #математика #геометрия #профильныйегэСкачать

Умножение вектора на число

Пусть нам дан вектор ( overrightarrow ) и действительное число ( k ) .

Определение Произведением вектора ( overrightarrow ) на действительное число ( k ) называется вектор ( overrightarrow ) удовлетворяющий следующим условиям:

Длина вектора ( overrightarrow ) равна ( left|overrightarrowright|=left|kright||overrightarrow| ) ;

Векторы ( overrightarrow ) и ( overrightarrow ) сонаправлены, при ( kge 0 ) и противоположно направлены, если ( kle 0 )

Обозначение: ( overrightarrow=koverrightarrow ) .

Видео:Нахождение длины вектора через координаты. Практическая часть. 9 класс.Скачать

Онлайн калькулятор. Сложение и вычитание двух векторов.

Этот онлайн калькулятор позволит вам очень просто найти сумму двух векторов или разность двух векторов для плоских и пространственных задач.

Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на сложение и вычитание двух векторов и закрепить пройденый материал.

Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Калькулятор для сложения и вычитания двух векторов

Введите значения векторов.

Инструкция использования калькулятора для сложения и вычитания двух векторов

Ввод даных в калькулятор для сложения и вычитания двух векторов

В онлайн калькулятор можно вводить числа или дроби. Более подробно читайте в правилах ввода чисел.

Дополнительные возможности калькулятора для сложения и вычитания двух векторов

• Между полями для ввода можно перемещаться нажимая клавиши «влево» и «вправо» на клавиатуре.

Видео:Сложение векторов. Правило параллелограмма. 9 класс.Скачать

Теория. Сложение и вычитание двух векторов

Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Видео:Сложение векторов. 9 класс.Скачать

Сумма векторов метод параллелограмма

Видео:сложение ВЕКТОРОВ вычитание ВЕКТОРОВ 9 класс геометрия АтанасянСкачать

Сложение векторов по правилу параллелограмма

Видео:Как находить угол между векторамиСкачать

Правило параллелограмма — что это такое

Чтобы сложить два вектора можно воспользоваться правилом параллелограмма.

Правило параллелограмма: если два неколлинеарных вектора a и b привести к общему началу, то вектор c=a+b совпадает с диагональю параллелограмма, построенного на векторах a и b. Начало вектора c совпадает с началом этих векторов.

Кроме того, по правилу параллелограмма можно осуществлять вычитание.

Видео:Выразить векторы. Разложить векторы. Задачи по рисункам. ГеометрияСкачать

Сложение векторов по правилу параллелограмма

Для того чтобы сложить два вектора по правилу параллелограмма, необходимо:

1. Взять произвольную точку А.
2. Отложить от точки векторы a и b.
3. Построить на векторах a и b параллелограмм.
4. Диагональ параллелограмма и будет суммой векторов a+b

Также существуют еще два правила нахождения векторной суммы:

1. Правило треугольника.

Чтобы сложить два вектора, нужно из произвольной точки отложить первый вектор, из его конца отложить второй вектор и построить вектор, который соединит начало первого с концом второго. Полученный вектор — искомая сумма.

2. Правило многоугольника.

Чтобы сложить несколько векторов, нужно от произвольной точки отложить первый вектор, из его конца — второй вектор, из конца второго — третий, и так далее. Затем соединить начальную точку с концом последнего вектора, полученный вектор — искомая сумма.

Видео:Сложение и вычитание векторов. Практическая часть. 11 класс.Скачать

Переместительный и сочетательный законы, доказательство

Для более ясного понимания правила параллелограмма, важно знать законы сложения векторов.

Переместительный закон: от перемены мест слагаемых сумма не меняется a+b=b+a.

От произвольной точки A отложим векторы AB=a и AD=b.

Построим параллелограмм ABCD.

По правилу треугольника заметим: AC=AB+BC, то есть равен сумме векторов a+b.

AC=AB+BC, AC=a+b⇒ a+b=b+a.

С другой стороны, AC=AD+DC, AC=b+a.

Что и требовалось доказать.

Именно переместительный закон применяется в правиле параллелограмма.

Сочетательный закон: (a+b)+c=a+(b+c).

От произвольной точки A отложим вектор AB=a, от точки B вектор BC=b, от точки C вектор CD=c.

Запишем сумму (a+b)+c через векторы:

Сумма AB+BC=AC (по правилу треугольника).

Запишем сумму a+(b+c) через векторы:

Что и требовалось доказать.

Видео:№770. Дан параллелограмм ABCD. Выразите вектор АС через векторы а и b , если:Скачать

Примеры решения задач

Дан параллелограмм, построенный на векторах AB=6 см, BC=8 см. ∠B=90º. Найти сумму векторов AB+BC.

По правилу параллелограмма сумма векторов AB+BC=BD.

BD-диагональ параллелограмма. Диагональ можно найти по формуле:

B D = √ ( A B ² + B C ² — 2 * A B * B C * cos B ) .

ABCD — прямоугольник, так как ∠B=90º ⇒cosB=0.

Видео:№335. Упростите выражение: a) AB+MN+BC+CA+PQ+NM; б) FK+MQ+KP+AM+QK+PFСкачать

Операции с векторами

Как сложить и перемножить векторы (и зачем).

Мы постепенно показываем вам математику за пределами школьной программы. Начинали со знакомства с векторами, теперь сделаем следующий шаг.

Напомним основные мысли:

• Вектор — это абстрактное понятие, которое представляет собой организованную последовательность каких-то чисел.
• В виде вектора можно представить координаты предмета в каком-то пространстве; площадь квартиры и её стоимость; цифровые данные анкеты какого-то человека и динамику цен на нефть.
• Если по-простому, то векторы нужны, чтобы обрабатывать большое количество организованных чисел. Представьте, что вектор — это коробка с конфетами, только вместо конфет — числа. Каждое число стоит в своей ячейке.
• Машинное обучение основано на перемножении матриц, которые, в свою очередь, можно представить как наборы векторов. Так что векторы лежат в глубине всех модных и молодёжных технологий ИИ.

С векторами можно совершать некоторые математические операции. Вот о них и поговорим.

Видео:Сложение векторов. Практическая часть. 9 класс.Скачать

Правильно — векторы

Математики часто говорят во множественном числе «вектора», но по словарю правильно «векторы». Это такой профессиональный жаргон, как «договора», «бухгалтера» и «сервера». Мы будем использовать «векторы», но если вы окажетесь в постковидном математическом баре, лучше говорите «вектора».

Видео:Скалярное произведение векторов. 9 класс.Скачать

Сложение

Представим четыре вектора, которые лежат в двухмерном пространстве и пока что не связаны между собой. Нарисуем эти векторы и обозначим их буквами X, Y, Z, K.

Поскольку векторы находятся в одном пространстве, координаты каждого состоят из одинакового количества чисел. У нас пример с двухмерным пространством и два числа. Выглядеть это будет так: X = (6, 4); Y = (3, −2); Z = (−7, −5); K = (−10, 4).

Векторы X, Y, Z, K в двухмерном пространстве

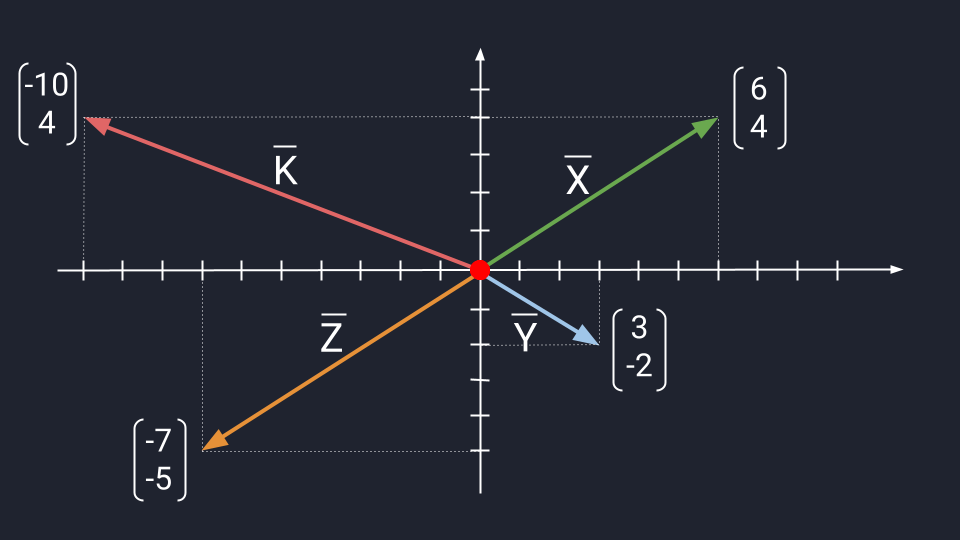
Если у нас несколько векторов с одинаковым количеством чисел, то эти числа можно поэлементно складывать. Для этого мы берём первое число одного вектора, складываем его с первым числом другого вектора и так далее.

Предположим, нам нужно сложить векторы X и Y.

X = (6, 4)
Y = (3, −2)
X + Y = (9, 2)

Вроде просто: складываешь последовательно все координаты, результаты сложения складываешь в исходные коробочки. Так можно делать с любым количеством координат. Помните, что вектор — это необязательно стрелка в двумерном пространстве. Она может быть и в десятимерном пространстве — с точки зрения математики это неважно.

Например, вот сложение векторов с пятью координатами:

X = (6, 4, 11, 14, 99)
Y = (3, -2, 10, -10, 1)
X + Y = (9, 2, 21, 4, 100)

Видео:10 класс, 40 урок, Сложение и вычитание векторовСкачать

Интуитивное изображение сложения

Для интуитивного восприятия удобно использовать векторы с двумя координатами. Их удобно рисовать на координатной плоскости и таким образом смотреть на геометрию.

Например, можно на плоскости показать, как будет работать сложение двух векторов. Для этого есть два метода: метод треугольника и метод параллелограмма.

Метод треугольника: ставим векторы Х и Y в очередь друг за другом. Для этого берём вектор Х, ставим за ним вектор Y и получаем новый вектор. Новый вектор начинается в хвосте вектора Х и заканчивается на стрелке вектора Y. Этот вектор — результат сложения. Представьте, что это ребёночек двух векторов.

Сложение векторов по методу треугольника: X = (6, 4); Y = (3, −2); Х + Y = (9, 2)

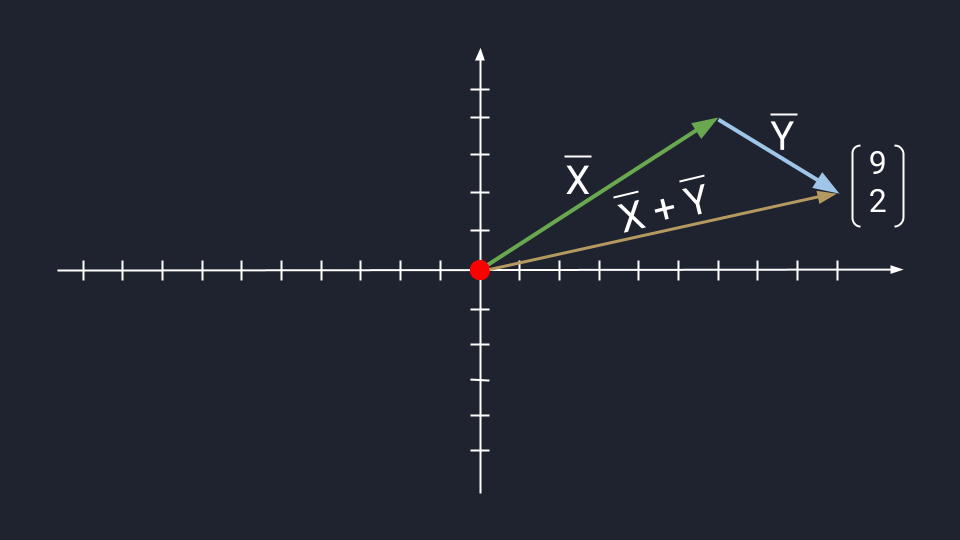
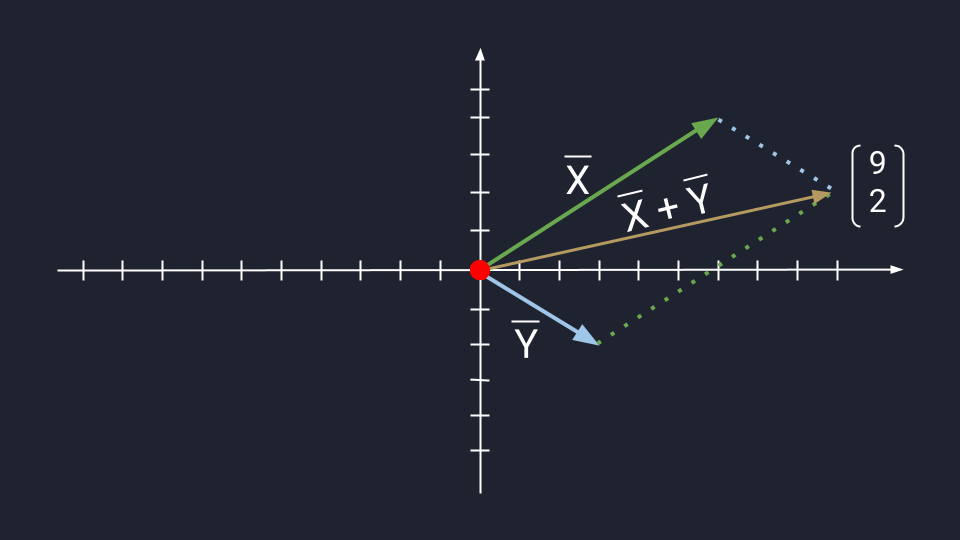
Чтобы воспользоваться методом параллелограмма, нам нужно поставить векторы Х и Y в одну исходную точку. Дальше мы дублируем векторы Х и Y, формируем параллелограмм и получаем новый вектор. В новом векторе соединяем исходную точку с исходной точкой дублирующих векторов — стрелка проходит посередине параллелограмма. Длина нового вектора — это сумма векторов Х и Y.

Сложение по методу параллелограмма и треугольника даёт одинаковый результат. Поэтому выбирайте вариант, который больше подходит под задачу.

Сложение векторов по методу параллелограмма: X = (6, 4); Y = (3, -2); Х + Y = (9, 2)

Видео:Разложение вектора по базису. 9 класс.Скачать

Вычитание

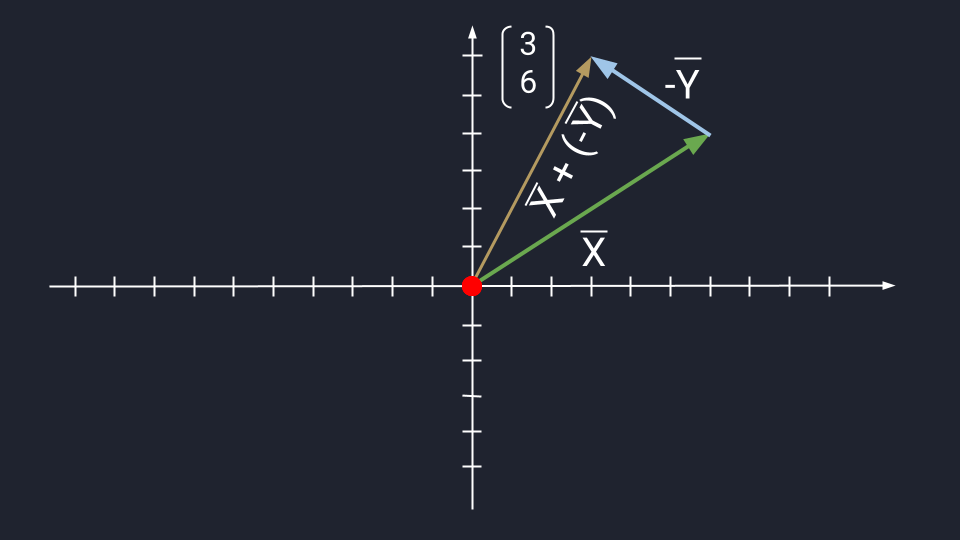
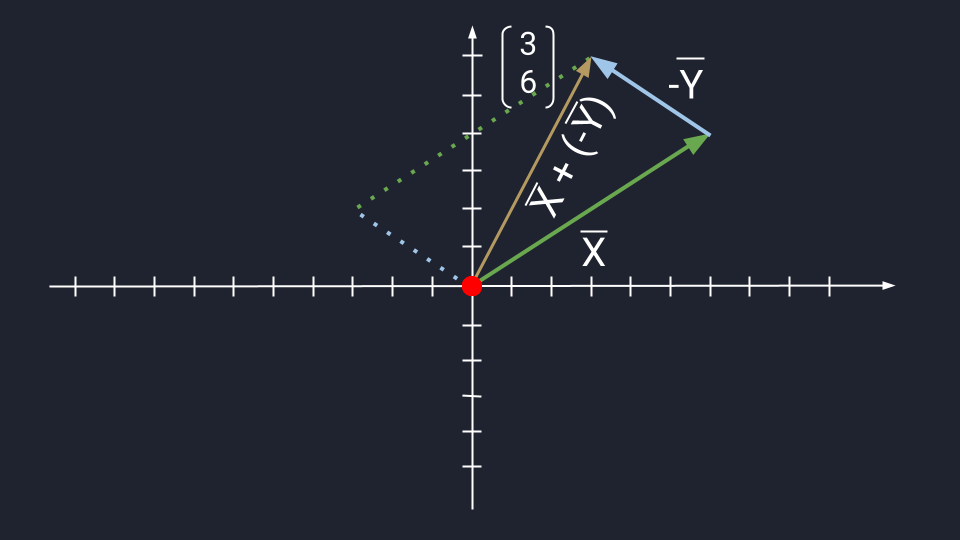
Вычитание векторов немного сложнее. Чтобы вычесть векторы, нужно «развернуть» вычитаемый вектор и сложить его с исходным. «Развернуть» — то есть направить в обратную сторону, «перевернув» знаки координат. Получится конструкция вроде такой: Х + (−Y)

Дальше используются правила сложения. Пошагово это выглядит так:

1. У нас есть X = (6, 4) и Y = (3, −2).
2. Превращаем формулу Х − Y в формулу Х + (−Y).
3. Разворачиваем вектор Y. Было: Y = (3, −2). Стало: −Y = (−3, 2).
4. Считаем: X + (−Y) = (3, 6).

Теперь посмотрим, как выглядит вычитание векторов на графике:

Вычитание векторов по методу треугольника: X = (6, 4); −Y = (−3, 2); X + (−Y) = (3, 6) Вычитание векторов по методу параллелограмма: X = (6, 4); −Y = (−3, 2); X + (−Y) = (3, 6)

Видео:Сложение векторов. Практическая часть. 9 класс.Скачать

Длина вектора

Длина вектора — это одно число, которое измеряется расстоянием от кончика до стрелки вектора. Длину вектора нельзя путать с координатами. Координаты — это несколько чисел, которые указывают на расположение стрелки вектора. По координатам можно определить только конечную точку вектора. Например, если X = (6, 2), то стрелка будет находиться в точке 6 по оси Х. Или другой пример: если Y = (6, 5), то стрелка этого вектора будет находиться в точке 5 по оси Y.

Предположим, нам известны начальные точки векторов X и Y. Пусть это будет точка 2 по оси X и точка 2 по оси Y. Так мы можем легко посчитать длину отрезков:

X = 6 − 2 = 4
Y = 5 − 2 = 3

Иногда приходится рассчитывать длину третьего вектора, который привязан к двум другим векторам. Это легко сделать с помощью теоремы Пифагора — это когда квадрат гипотенузы равен сумме квадратов катетов. В нашем случае катетами будут длины векторов X и Y. Вспоминаем школьную формулу и считаем:

|C|2 = 42 + 32 = 25
|C| = √25 = 5 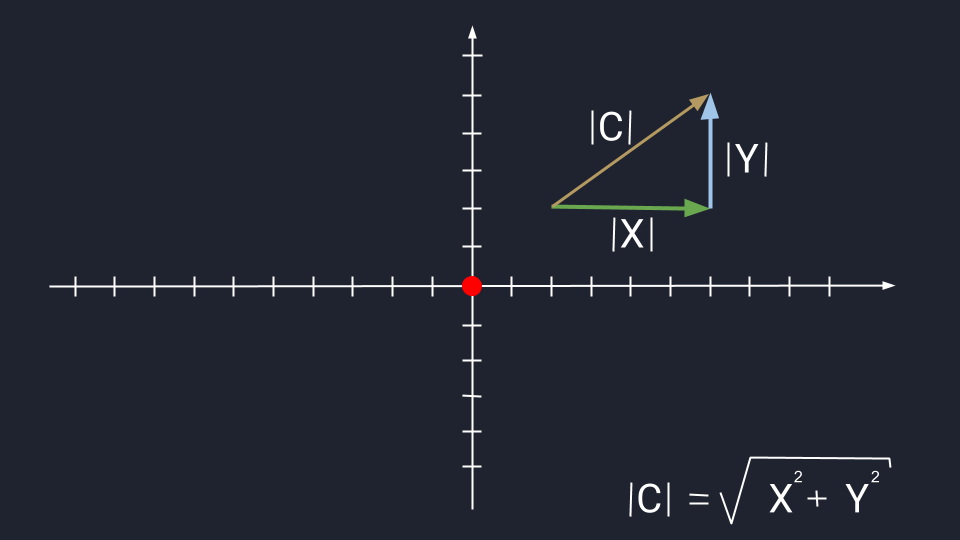Длина вектора считается по формуле прямоугольного треугольника. Чтобы было проще представить — перенесите векторы на систему координат

Это формула для двумерного пространства. В трёхмерном пространстве формула похожая: нужно сложить квадраты трёх координат и вычислить квадратный корень из суммы.

В пространстве с большим числом измерений формула выглядит сложнее, но по сути то же: складываем все квадраты координат и получаем квадратный корень из этой суммы.

Видео:2 урок. Сложение и вычитание векторов | Геометрия. 9 классСкачать

Умножение и деление вектора на число

Умножение и деление позволяют изменить длину и направление вектора. Если мы умножим вектор Х на три, то увеличим его длину в три раза. Если умножим на минус три — увеличим длину и изменим его направление на противоположное.

Умножение вектора на число

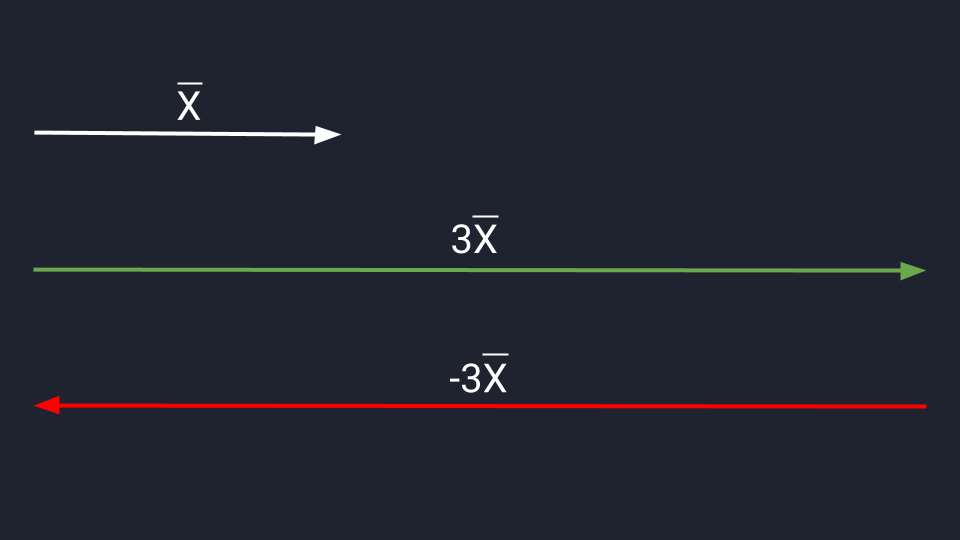
Для деления сохраняются аналогичные правила. Делим вектор Х на три и сокращаем длину в три раза. Делим на минус три — сокращаем и разворачиваем.

Деление вектора на число

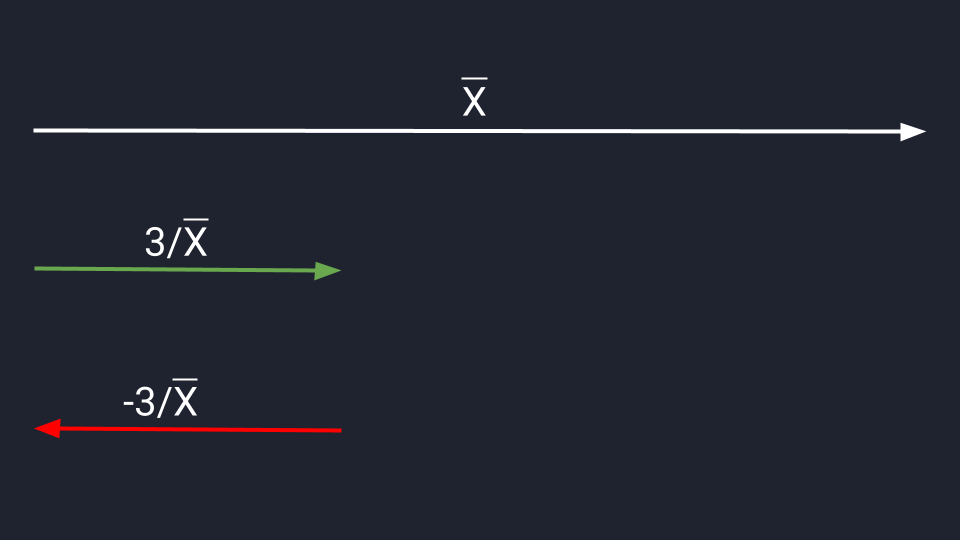
Видео:Вычитание векторов. Практическая часть. 9 класс.Скачать

Да вроде несложно!

Пока ничего сложного. Но если углубляться, вы узнаете, что:

• векторы можно умножать на векторы тремя способами в зависимости от задачи и от того, что мы понимаем под умножением;
• если от векторов перейти к матрицам, то перемножение матриц имеет несколько более сложную и довольно неинтуитивную математику;
• а перемножение матриц — это и есть машинное обучение.

Что дальше

В следующей статье рассмотрим линейную зависимость векторов. Чтобы не скучать — посмотрите интервью с Анастасией Никулиной. Анастасия сеньор-дата-сайентист в Росбанке и по совместительству блогер с интересной историей.

Сложение векторов

Часть математических и физических задач содержит необходимость математических действий с векторами (сложение и вычитание).

Проиллюстрируем сложение. Пусть даны вектора и , попытаемся найти вектор .

Способ 1. Метод сложения треугольником

Возьмём необходимые вектора и параллельным переносом совместим конец первого вектора ( ) и начало второго ( ) (рис. 1)

Рис. 1. Сложение векторов (правило треугольника)

Тогда вектор, соединяющий начальную точку первого вектора ( ) и конец второго ( ), является вектором ( ).

Способ 2. Метод сложения параллелограммом

Возьмём необходимые вектора и параллельным переносом совместим начало первого вектора ( ) и начало второго ( ) (рис. 2). Параллельным переносом совместим конец каждого вектора с началом другого.

Рис. 2. Сложение векторов (правило параллелограмма)

Тогда вектор, соединяющий общую начальную точку первого ( ) и второго ( ) векторов и общий конец данных векторов, является вектором суммы ( ).

Вывод: в ряде задач, где присутствуют несколько однородных векторных физических величин, часто необходимо найти общий вектор (общую скорость, равнодействующую силу, полный вектор магнитной индукции или электрической напряжённости поля). Тогда необходимо сначала сложить вектора, а потом найти модуль получившегося вектора.Чаще всего первый метод используется в кинематике (сложение скоростей). Второй метод часто используют в динамике.