Сложи данные векторы используй параллелепипед и вспомни о законах сложения векторов в плоскости cd

Правило параллелограмма >>

Сложение векторов. Чтобы сложить 2 вектора, необходимо от произвольной точки отложить вектор, равный первому, затем от конца полученного вектора отложить вектор равный второму и соединить начало 1-ого и конец 2-ого (по правилу треугольника): Правило треугольника:

Слайд 18 из презентации «ВЕКТОРЫ в пространстве»

Размеры: 720 х 540 пикселей, формат: .jpg. Чтобы бесплатно скачать слайд для использования на уроке, щёлкните на изображении правой кнопкой мышки и нажмите «Сохранить изображение как. ». Скачать всю презентацию «ВЕКТОРЫ в пространстве.ppt» можно в zip-архиве размером 356 КБ.

Похожие презентации

«Векторы геометрия 10 класс» — Вектора. М – точка пересечения медиан. Вектор – как направленный отрезок. Вырази вектор АВ через вектора ОС и ОD. Сумма векторов. Произведение векторов. Вырази вектор. Выразите вектор ОМ. Действия с векторами. Векторы в пространстве.

«Вектор решение задач» — Выразить векторы AE, AK, KE через векторы а и b. BE : EC = 3 : 1. K – середина DC. № 2 Выразить векторы DP, DM, AC через векторы а и b. Выразить векторы AM, DA, CA, MB, CD через вектор a и вектор b. СР : PD = 2 : 3; AK : KD = 1 : 2. Выразить векторы СК, РК через векторы а и b. Применение векторов к решению задач (ч.1).

«Компланарные векторы» — Определение. Утверждение, обратное признаку компланарности векторов: Три вектора, среди которых имеются два коллинеарных, также компланарны. Любые два вектора компланарны. Мы умеем на плоскости складывать векторы по правилу треугольника и параллелограмма. Признак компланарности трех векторов: Компланарные векторы.

«Координаты вектора» — 1. Координаты суммы векторов равны сумме соответствующих координат. 2. Свойства координат вектора. Координаты вектора. A(3; 2). 1. Координаты вектора. 2. Координаты разности векторов равны разности соответствующих координат.

«Векторы в пространстве» — a+b=b+a (переместительный закон). Умножение вектора на число. Коллинеарные векторы — это векторы, лежащие на одной или на параллельных прямых. Вектор — это направленный отрезок. Если векторы сонаправлены и их длины равны, то эти векторы называются равными. Геометрия. (Kl) a =k (la) — сочетательный закон.

«Вектор геометрия» — Зная, как выполняется сложение векторов и умножение вектора на число. 3. Равенство, коллинеарность, противоположность и одинаковость направления векторов. Если один из векторов нулевой скалярное произведение считается равным нулю. 1. Введение. Название работы отражает содержание и смысл, который раскрыт более тщательно.

Правило параллелепипеда. Разложение вектора

Вы будете перенаправлены на Автор24

Правило параллелепипеда

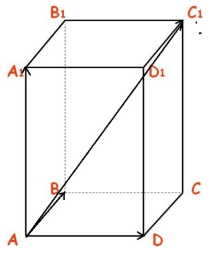
Для правила сложения трех векторов рассмотрим следующую задачу.

Дан прямоугольный параллелепипед $ABCDA_1B_1C_1D_1$. Доказать, что $overrightarrow+overrightarrow+overrightarrow=overrightarrow$

Доказательство.

Воспользуемся свойством правила треугольника сложения двух векторов $overrightarrow+overrightarrow=overrightarrow$, получим:

Так как $overrightarrow=overrightarrow, overrightarrow=overrightarrow$

Из этой задачи получаем следующее правило для нахождения сложения трех векторов. Чтобы найти сумму трех векторов $overrightarrow,overrightarrow и overrightarrow$ нужно от произвольной точки $O$ отложить векторы $overrightarrow=overrightarrow$, $overrightarrow=overrightarrow$ и $overrightarrow=overrightarrow$ и построим параллелепипед на этих векторах. Тогда вектор диагонали $overrightarrow$ и будет суммой этих трех векторов. Это правило называется правилом параллелепипеда для сложения трех векторов.

Разложение вектора по двум неколлинеарным векторам

Вспомним сначала, какие векторы называются компланарными.

Два вектора, которые параллельны одной плоскости называются компланарными.

Произвольный вектор $overrightarrow

$ можно разложить по трем некомпланарным векторам $overrightarrow, overrightarrow$ и $overrightarrow$ с единственными коэффициентами разложения.

Математически это можно записать следующим образом

Доказательство.

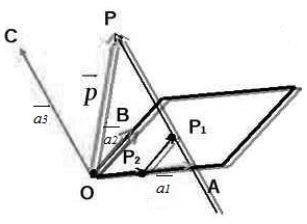
Существование: Пусть нам даны три некомпланарных вектора $overrightarrow, overrightarrow$ и $overrightarrow$. Выберем произвольную точку $O$ и построим следующие векторы:

[overrightarrow=overrightarrow, overrightarrow=overrightarrow, overrightarrow=overrightarrow и overrightarrow

=overrightarrow]

Рассмотрим следующий рисунок:

Произведем следующие дополнительные построения. Проведем через точку $P$ прямую, которая будет параллельна вектору $overrightarrow$. Пусть эта прямая пересекает плоскость $OAB$ в точке $P_1$. Далее, проведем через точку $P_1$ прямую, которая будет параллельна вектору $overrightarrow$. Пусть эта прямая пересекает прямую $OA$ в точке $P_2$ (смотри рисунок выше).

Воспользуемся свойством правила треугольника сложения двух векторов $overrightarrow+overrightarrow=overrightarrow$, получим:

Так как векторы $overrightarrow$ и $overrightarrow$ коллинеарны, то

Так как векторы $overrightarrow

$ и $overrightarrow$ коллинеарны, то

Так как векторы $overrightarrow

$ и $overrightarrow$ коллинеарны, то

Тогда, получаем, что

Существование разложения доказано.

Единственность: Предположим противное. Пусть существует еще одно разложение вектора $overrightarrow

$ по векторам $overrightarrow, overrightarrow$ и $overrightarrow$:

Вычтем эти разложения друг из друга

Из этого получаем

Теорема доказана.

Сложение и вычитание векторов

Теорема 1 От любой точки ( K ) можно отложить вектор единственный ( overrightarrow ) .

Существование: Имеем два следующих случая:

Здесь получаем, что искомый нами вектор совпадает с вектором ( overrightarrow ) .

Из данного выше построения сразу же будет следовать единственность данного вектора.

Сумма векторов. Сложение векторов. Правило треугольника

Сложение векторов выполняется по правилу треугольника или по правилу параллелограмма.

Суммой нескольких векторов ( vec ) , ( vec ) , ( vec,;ldots ) называется вектор ( vec ) , получающийся в результате последовательного сложения данных векторов.

Такая операция выполняется по правилу многоугольника.

Сумма векторов в координатах
При сложении двух векторов соответствующие координаты складываются.
( vec + vec = left( <+ , + , + > right) )

Отметим несколько свойств сложения двух векторов:

Для произвольного вектора ( overrightarrow ) выполняется равенство

Для произвольных точек ( A, B и C ) справедливо следующее равенство

Замечание Таким способом также можно строить сумму любого числа векторов. Тогда оно будет носить название правила многоугольника.

Разность векторов. Вычитание векторов

Разность двух одинаковых векторов равна нулевому вектору :
( vec — vec = vec )

Длина нулевого вектора равна нулю:
( left| vec right| = 0 )

Разность векторов в координатах
При вычитании двух векторов соответствующие координаты также вычитаются.
( vec — vec = left( <- , — , — > right) )

Умножение вектора на число

Пусть нам дан вектор ( overrightarrow ) и действительное число ( k ) .

Определение Произведением вектора ( overrightarrow ) на действительное число ( k ) называется вектор ( overrightarrow ) удовлетворяющий следующим условиям:

Длина вектора ( overrightarrow ) равна ( left|overrightarrowright|=left|kright||overrightarrow| ) ;

Векторы ( overrightarrow ) и ( overrightarrow ) сонаправлены, при ( kge 0 ) и противоположно направлены, если ( kle 0 )

Обозначение: ( overrightarrow=koverrightarrow ) .

💡 Видео