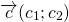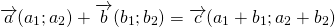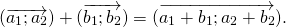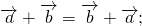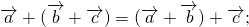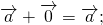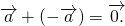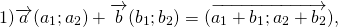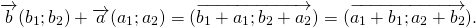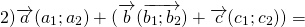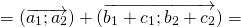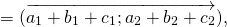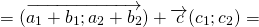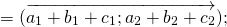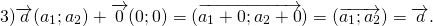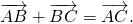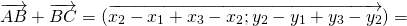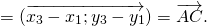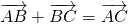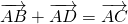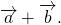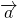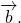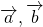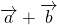Сложение векторов треугольник доказательство

Вы будете перенаправлены на Автор24

Видео:СЛОЖЕНИЕ ВЕКТОРОВ закон правило треугольника 9 класс АтанасянСкачать

Откладывание вектора от данной точки

Для того, чтобы ввести сумму векторов, сначала необходимо разобраться в таком понятии, как откладывание вектора от данной точки.

Введем следующую теорему:

От любой точки $K$ можно отложить вектор $overrightarrow$ и притом только один.

Доказательство.

Существование: Здесь нужно рассмотреть два случая:

В этом случае, очевидно, что искомый вектор — вектор $overrightarrow$.

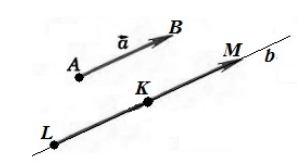
Рисунок 2. Иллюстрация теоремы 1

Единственность: единственность сразу следует из построения, проведенного в пункте «существование».

Теорема доказана.

Видео:СУММА ВЕКТОРОВ правило треугольникаСкачать

Сложение векторов. Правило треугольника

Пусть нам даны векторы $overrightarrow$ и $overrightarrow$.

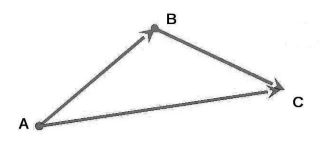
Рисунок 3. Сумма векторов

Готовые работы на аналогичную тему

Иначе, определение 2, еще называют правилом треугольника для сложения двух векторов.

Из этого правила следует несколько свойств сложения двух векторов:

Для любого вектора $overrightarrow$ выполняется равенство

Для любых произвольных точек $A, B и C$ выполняется равенство

Аналогично правилу треугольника можно строить сумму любого количества векторов. Такое правило сложения называется правилом многоугольника.

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Правило параллелограмма

Помимо правила треугольника для сложения двух векторов, есть еще правило параллелограмма для сложения двух векторов. Сформулируем и докажем для начала следующую теорему.

Доказательство.

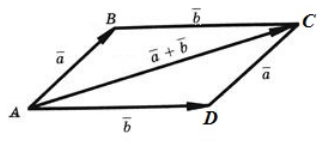
Переместительный закон:

Рисунок 4. Иллюстрация переместительного закона

Тогда выполнение переместительно закона будет очевидно вытекать из равенства длин $left|overrightarrow+overrightarrowright|и |overrightarrow+overrightarrow|$.

Сочетательный закон:

Рисунок 5. Иллюстрация сочетательного закона

Из свойства правила треугольника $overrightarrow+overrightarrow=overrightarrow$, получим:

Теорема доказана.

Видео:Как доказать теорему о медианах треугольника с использованием методов векторной алгебры?Скачать

Пример задачи на сложение векторов

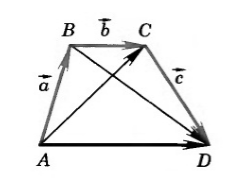
Дан четырехугольник $ABCD$. Доказать, что $overrightarrow+overrightarrow+overrightarrow=overrightarrow$

Доказательство.

Воспользуемся свойством правила треугольника $overrightarrow+overrightarrow=overrightarrow$, получим:

ч. т. д.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 01 04 2022

Видео:Сложение векторов. 9 класс.Скачать

Сложение векторов

Сумма векторов

Свойства сложения векторов:

Для любых векторов

3) свойство прибавления нулевого вектора:

4) сумма противоположных векторов равна нулевому вектору:

Достаточно сравнить координаты векторов, стоящих в левой и правой частях этих равенств:

Так как соответствующие координаты равны, то эти векторы равны.

(О сложении векторов)

Каковы бы ни были точки A, B, C, имеет место векторное равенство:

Что и требовалось доказать.

Правило треугольника построения суммы двух векторов

Чтобы построить сумму двух векторов по правилу треугольника, надо от конца одного вектора отложить другой вектор и провести вектор от начала первого к концу второго вектора.

Например,

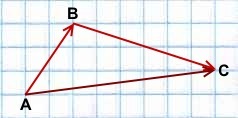
(то есть это правило следует из теоремы о сложении векторов).

Правило параллелограмма построения суммы двух векторов

Чтобы построить сумму двух векторов по правилу параллелограмма, надо отложить эти векторы от общего начала. Сумма векторов есть диагональ параллелограмма, построенного на этих векторах и имеющая с ними общее начало.

Например,

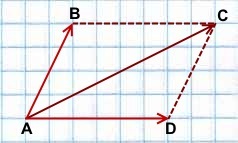
Правило параллелограмма построения суммы векторов применяется лишь для неколлинеарных векторов.

При любом способе построения суммы неколлинеарных векторов получим одинаковый результат.

Построить сумму векторов

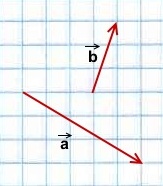
1) Чтобы построить сумму векторов по правилу треугольника, отложим от конца вектора

Сумма этих векторов равна вектору, проведённому от начала первого вектора (a) к концу второго (b).

2) Чтобы построить сумму векторов по правилу параллелограмма, отложим векторы

от общего начала.

Достроим на этих векторах параллелограмм.

Сумма

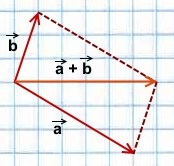
равна вектору, лежащему на диагонали параллелограмма и имеющему с ними общее начало.

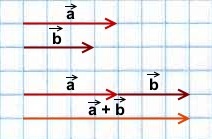
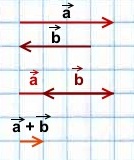
1) Сумма двух сонаправленных коллинеарных векторов равна вектору, сонаправленному этим векторам, длина которого равна сумме длин данных векторов.

2) Сумма двух противоположно направленных векторов равна вектору, направление которого совпадает с направлением вектора, модуль которого больше, а длина равна разности этих векторов.

Фактически в обоих случаях мы используем правило треугольника сложения векторов:

от конца первого вектора откладываем вектор, равный второму, и строим сумму как вектор в направлении от начала первого вектора к концу второго.

Из неравенства треугольника следует ещё два свойства сложения векторов:

Видео:8 класс, 44 урок, Законы сложения векторов. Правило параллелограммаСкачать

Сумма и разность векторов

В данной публикации мы рассмотрим, как найти сумму и разность векторов, приведем геометрическую интерпретацию, а также формулы, свойства и примеры этих действий.

Видео:Сложение векторов. Правило параллелограмма. 9 класс.Скачать

Сумма векторов

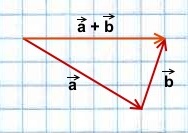
Сложение векторов выполняется по правилу треугольника.

Геометрическая интерпретация:

Суммой a и b является вектор c , начало которого совпадает с началом a , а конец – с концом b . При этом конец вектора a должен совпадать с началом вектора b .

Для сложения векторов также используется правило параллелограмма.

Два неколлинеарных вектора a и b можно привести к общему началу, и в этом случае их суммой является вектор c , совпадающий с диагональю параллелограмма и берущий начало в той же точке, что и исходные векторы.

Формула сложения векторов

Элементы вектора c равняются попарной сумме соответствующих элементов a и b .

<table data-id="250" data-view-id="250_55602" data-title="Формулы сложения векторов" data-currency-format="$1,000.00" data-percent-format="10.00%" data-date-format="DD.MM.YYYY" data-time-format="HH:mm" data-features="["after_table_loaded_script"]" data-search-value="" data-lightbox-img="" data-head-rows-count="1" data-pagination-length="50,100,All" data-auto-index="off" data-searching-settings="» data-lang=»default» data-override=»» data-merged=»[]» data-responsive-mode=»2″ data-from-history=»0″>

Для плоских задач

<td data-cell-id="B1" data-x="1" data-y="1" data-db-index="1" data-cell-type="text" data-original-value=" a + b = <a_x + b_x; a_y + b_y> » data-order=» a + b = <a_x + b_x; a_y + b_y> » style=»min-width:55.0847%; width:55.0847%;»> a + b = <a_x + b_x; a_y + b_y>Для трехмерных задач

<td data-cell-id="B2" data-x="1" data-y="2" data-db-index="2" data-cell-type="text" data-original-value=" a + b = <a_x + b_x; a_y + b_y; a_z + b_z> » data-order=» a + b = <a_x + b_x; a_y + b_y; a_z + b_z> «> a + b = <a_x + b_x; a_y + b_y; a_z + b_z>Для n-мерных векторов

<td data-cell-id="B3" data-x="1" data-y="3" data-db-index="3" data-cell-type="text" data-original-value=" a + b = <a₁ + b₁; a₂ + b₂; . a_n + b_n> » data-order=» a + b = <a₁ + b₁; a₂ + b₂; . a_n + b_n> «> a + b = <a₁ + b₁; a₂ + b₂; . a_n + b_n>

Свойства сложения векторов

1. Коммутативность: a + b = b + a

2. Ассоциативность: ( a + b ) + c = a + ( b + c )

3. Прибавление к нулю: a + 0 = a

4. Сумма противоположных векторов: a + (- a ) = 0

Примечание: Вектор – a коллинеарен и равен по длине a , но имеет противоположное направление, из-за чего называется противоположным.

Видео:Сложение векторов методом треугольникаСкачать

Разность векторов

Для вычитания векторов также применяется правило треугольника.

Если из вектора a вычесть b , то получится c , причем должно соблюдаться условие:

Формула вычитания векторов

Элементы вектора c равны попарной разности соответствующих элементов a и b .

<table data-id="251" data-view-id="251_83403" data-title="Формулы вычитания векторов" data-currency-format="$1,000.00" data-percent-format="10.00%" data-date-format="DD.MM.YYYY" data-time-format="HH:mm" data-features="["after_table_loaded_script"]" data-search-value="" data-lightbox-img="" data-head-rows-count="1" data-pagination-length="50,100,All" data-auto-index="off" data-searching-settings="» data-lang=»default» data-override=»» data-merged=»[]» data-responsive-mode=»2″ data-from-history=»0″>

Для плоских задач

<td data-cell-id="B1" data-x="1" data-y="1" data-db-index="1" data-cell-type="text" data-original-value=" a — b = <a_x — b_x; a_y — b_y> » data-order=» a — b = <a_x — b_x; a_y — b_y> » style=»min-width:55.0847%; width:55.0847%;»> a — b = <a_x — b_x; a_y — b_y>Для трехмерных задач

<td data-cell-id="B2" data-x="1" data-y="2" data-db-index="2" data-cell-type="text" data-original-value=" a — b = <a_x — b_x; a_y — b_y; a_z — b_z> » data-order=» a — b = <a_x — b_x; a_y — b_y; a_z — b_z> «> a — b = <a_x — b_x; a_y — b_y; a_z — b_z>Для n-мерных векторов

<td data-cell-id="B3" data-x="1" data-y="3" data-db-index="3" data-cell-type="text" data-original-value=" a — b = <a₁ — b₁; a₂ — b₂; . a_n — b_n> » data-order=» a — b = <a₁ — b₁; a₂ — b₂; . a_n — b_n> «> a — b = <a₁ — b₁; a₂ — b₂; . a_n — b_n>

Видео:Сложение векторов теорема.Скачать

Примеры задач

Задание 1
Вычислим сумму векторов и .

Задание 2
Найдем разность векторов и .

🔍 Видео

Урок 4. Векторы. Сложение векторов. Правило треугольника. Правило параллелограмма.Скачать

Геометрия 9 класс (Урок№2 - Сумма двух векторов. Законы сложения векторов.)Скачать

Сложение векторов. Правило треугольникаСкачать

Сложение и вычитание векторов. Практическая часть. 11 класс.Скачать

Вычитание векторов. 9 класс.Скачать

Сложение нескольких векторов. Правило многоугольникаСкачать

18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Математика без Ху!ни. Смешанное произведение векторовСкачать

ТОПОВЫЙ СПОСОБ СЛОЖЕНИЯ ВЕКТОРОВСкачать

Сумма двух векторов. Правило треугольника. Законы сложения векторов. Правило параллелограмма.Скачать

Задача, которую боятсяСкачать