Следствия из признаков параллельных прямых (4 видео)

Свойства параллельных прямых

Средняя оценка: 4.3

Всего получено оценок: 174.

Средняя оценка: 4.3

Всего получено оценок: 174.

Свойства параллельных прямых крайне часто встречаются при решении задач и доказательств теорем. Произвольные прямые – редкость, но есть такие фигуры, как квадрат или параллелограмм, где параллельные прямые могут стать основой задачи, а без знания свойств параллельных прямых решить такие задачи невозможно.

Содержание

Что такое свойства параллельных прямых
Две группы свойств параллельных прямых
Следствия из аксиомы параллельных прямых
Следствие 1
Следствие 2
Следствия из признаков параллельности
Что мы узнали?
Признаки и свойства параллельных прямых
Признаки параллельных прямых
Свойства параллельных прямых
Свойства параллельных прямых
🌟 Видео

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Что такое свойства параллельных прямых

Для начала выделим определения, которые необходимо знать для изучения свойств параллельных прямых.

Параллельные прямые это прямые, которые не имеют общих точек, или прямые, которые не пересекаются и лежат в одной плоскости.

Пересечение означает, что у двух объектов есть общая точка или набор точек. Поэтому когда в геометрии говорят, что прямые имеют общую точку, имеется в виду, что они пересекаются.

При пересечении двух прямых секущей, образуются накрест лежащие, соответственные и односторонние углы.

Существует аксиома параллельных прямых, которая крайне важна при доказательстве некоторых свойств и является основным свойством параллельных прямых. Аксиома гласит, что через точку на плоскости можно провести только одну прямую, параллельную данной.

Видео:7 класс, 25 урок, Признаки параллельности двух прямыхСкачать

Две группы свойств параллельных прямых

Свойств у параллельных прямых всего 5, но они делятся на две большие группы: следствия из аксиомы параллельных прямых и следствия из признаков параллельности прямых. Начнем с первой группы.

Следствия из аксиомы параллельных прямых

Следствие 1

Если одна из двух параллельных прямых, параллельна третьей, то и другая прямая ей параллельна.

Кажется, что это логично и не требует доказательства. Но в геометрии количество утверждений, не требующих обоснования, крайне мало, и каждое из них носит название – аксиома.

Аксиомы были выведены еще на заре геометрии и с тех пор мало что изменилось. Большая часть современных теорем выведена на основании аксиом Древней Греции. Эти утверждения единственные, что в математике не требует доказательства.

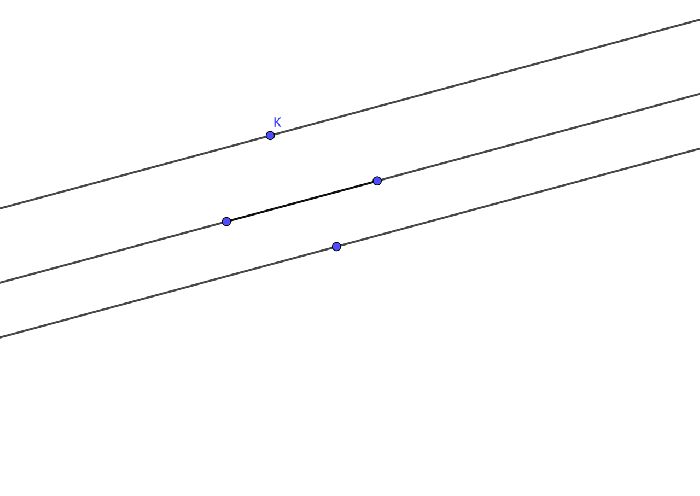
Проведем две параллельные прямые а и b. Прямая с параллельна прямой а. Предположим, что при этом с не параллельна прямой b. Тогда у нее должна быть какая-то точка пересечения К. То есть через точку К проходит две прямые с и b. При этом каждая из этих прямых должна быть параллельна прямой а.

То есть, через одну точку на плоскости проведены две прямые, параллельные данной. Это невозможно, потому что противоречит аксиоме параллельных прямых. Значит изначальное предположение было неверным и прямые с и b параллельны.

Рис. 1. Иллюстрация следствия.

Следствие 2

Следствие 2 очень важно, так как говорит о секущей двух параллельных прямых. Свойство гласит: если прямая пересекает одну из параллельных прямых, то она пересечет и вторую.

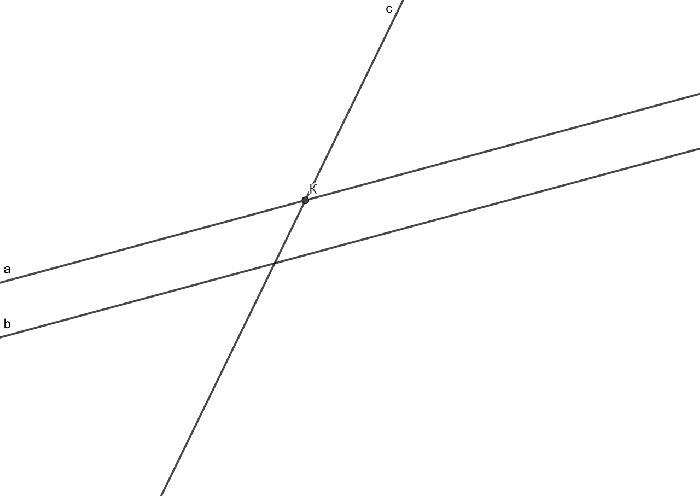
Доказательство также ведется методом от противного. Проведем две прямые: а и b. Представим, что прямая с пересекает прямую а, но не пересекает прямую b. Тогда прямые c и b параллельны. При этом с пересекает а, то есть у этих прямых есть общая точка К.

Тогда через точку К проходит прямая а и прямая с, но каждая из них параллельна b. Значит, через одну точку проходит две прямых параллельных прямой b, а это невозможно по аксиоме параллельных прямых. Значит изначальное предположение было неверным и прямая с пересекает каждую из прямых а и b, что и требовалось доказать.

Рис. 2. Рисунок к доказательству.

Следствия из признаков параллельности

Эту группу запомнить проще всего. Свойств параллельности прямых всего 3 и каждому из них соответствует свое следствие.

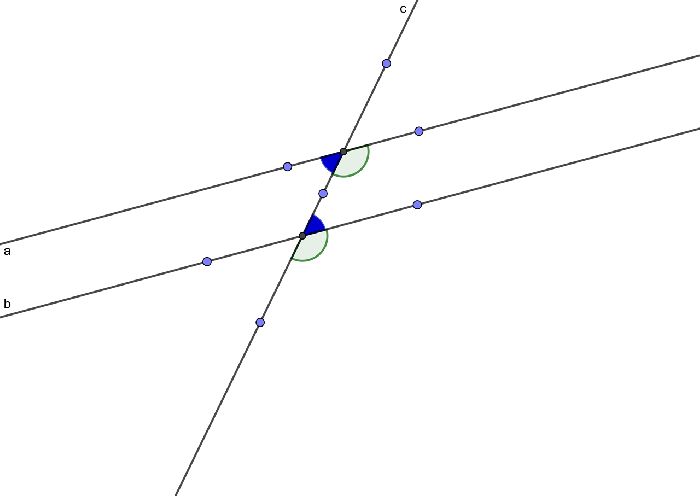
Прямые параллельны, если накрест лежащие углы при секущей равны. Следствие вполне логично: Накрест лежащие углы при двух параллельных прямых и секущей равны.
Прямые параллельны, если соответственные углы равны. Следствие: соответственные углы при параллельных прямых и секущей равны.
Прямые параллельны, если сумма односторонних углов равна 180. Следствие: сумма односторонних углов при параллельных прямых и секущей равны 180

Рис. 3. Иллюстрация признаков.

Видео:Геометрия 7 класс (Урок№19 - Признаки параллельности прямых.)Скачать

Что мы узнали?

Мы дали понятие параллельным прямым, выделили две большие группы свойств параллельных прямых и доказали два свойства. Разобрались с использованием аксиомы параллельных прямых при доказательстве теорем в геометрии.

Видео:Урок 13 Признаки параллельности прямых (7 класс)Скачать

Признаки и свойства параллельных прямых

Видео:7 класс, 28 урок, Аксиома параллельных прямыхСкачать

Признаки параллельных прямых

1. Если две прямые параллельны третьей прямой, то они являются параллельными:

2. Если две прямые перпендикулярны третьей прямой, то они параллельны:

Остальные признаки параллельности прямых основаны на углах, образующихся при пересечении двух прямых третьей.

3. Если сумма внутренних односторонних углов равна 180°, то прямые параллельны:

Если ∠1 + ∠2 = 180°, то a || b.

4. Если соответственные углы равны, то прямые параллельны:

5. Если внутренние накрест лежащие углы равны, то прямые параллельны:

Видео:Геометрия 7 класс (Урок№20 - Аксиома параллельных прямых.)Скачать

Свойства параллельных прямых

Утверждения, обратные признакам параллельности прямых, являются их свойствами. Они основаны на свойствах углов, образованных пересечением двух параллельных прямых третьей прямой.

1. При пересечении двух параллельных прямых третьей прямой, сумма образованных ими внутренних односторонних углов равна 180°:

Если a || b, то ∠1 + ∠2 = 180°.

2. При пересечении двух параллельных прямых третьей прямой, образованные ими соответственные углы равны:

3. При пересечении двух параллельных прямых третьей прямой, образованные ими накрест лежащие углы равны:

Следующее свойство является частным случаем для каждого предыдущего:

4. Если прямая на плоскости перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой:

Пятое свойство — это аксиома параллельности прямых:

5. Через точку, не лежащую на данной прямой, можно провести только одну прямую, параллельную данной прямой:

Видео:Геометрия 7 класс (Урок№21 - Свойства параллельных прямых.)Скачать

Свойства параллельных прямых

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

С помощью данного видеоурока вы сможете самостоятельно изучить тему «Свойства параллельных прямых». В ходе него вам предстоит параллельные прямые, рассмотреть их свойства, а также сформулировать одну из самых важных аксиом геометрии.

Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок «Основы геометрии»