«Кенгуру» — это массовый международный конкурс-игра для школьников под девизом «Математика для всех». Главная цель конкурса — привлечь как можно больше ребят к решению математических задач, показать каждому школьнику, что обдумывание задачи может быть делом живым, увлекательным, и даже веселым!
- Кенгуру 2021 ответы и задания для 7-8 класса
- Задание 1
- Задание 2
- Задание 3
- Задание 4
- Задание 5
- Задание 6
- Задание 7
- Задание 8
- Задание 9
- Задание 10
- Задание 11
- Задание 12
- Задание 13
- Задание 14
- Задание 15
- Задание 16
- Задание 17
- Задание 18
- Задание 19
- Задание 20
- Задание 21
- Задание 22
- Задание 23
- Задание 24
- ГДЗ по математике 2 класс учебник Рудницкая, Юдачева часть 2 Страница 4-15
- Четырехугольники
- теория по математике 📈 планиметрия
- Выпуклый четырехугольник
- Виды и свойства выпуклых четырехугольников
- Прямоугольник
- Квадрат
- Параллелограмм
- Трапеция
- Виды трапеций
- Средняя линия трапеции
- 🔥 Видео
Видео:ОГЭ как найти тангенс угла, если нет треугольника #математика #огэ #огэматематика #геометрияСкачать

Кенгуру 2021 ответы и задания для 7-8 класса
Очередной конкурс «Кенгуру» состоится 18 марта 2021 года. Конкурс проходит один раз в год — в третий четверг марта, проводится он обязательно в школе, подробная информация по ссылке на официальную страницу организатора конкурса: Кенгуру
Ниже представляем первые 10 заданий Кенгуру для 7-8 класса и ответы к ним, обсуждаем остальные задания и ответы в комментариях.
Задачи на 3 балла
Задание 1
В некотором четырехугольнике 1; 2; 2, 8; 5; 7,5 – длины сторон и одной из диагоналей. Какое из этих чисел длина диагонали?
Варианты ответов: (А) 1; (Б) 2; (В) 2,8; (Г) 5; (Д) 7,5.
Наш вариант ответа: (В) 2,8
Задание 2
Какой из следующих символов знаков Зодиака имеет ось симметрии?
Варианты ответов: (А) Стрелец; (Б) Скорпион; (В) Лев; (Г) Рак; (Д) Козерог.
Наш вариант ответа: (А) Стрелец
Задание 3
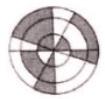
На рисунке показаны три концентрических круга с четырьмя линиями, проходящими через их общий центр. Какой процент фигуры закрашен серым?
Варианты ответов: (А) 30%; (Б) 35%; (В) 40%; (Г) 45%; (Д) 50%.
Наш вариант ответа: (Д) 50%
Задание 4
Сколько есть четырехзначных чисел, цифры в которых идут слева-направо подряд в возрастающем порядке?
Варианты ответов: (А) 5; (Б) 6; (В) 7; (Г) 8; (Д) 9.
Наш вариант ответа: (Б) 6
Задание 5
Если правильно сложить кусочки, получится разность. Чему она равна?
Варианты ответов: (А) -100; (Б) -8; (В) -1; (Г) 199; (Д) 208.
Наш вариант ответа: (А) -100
Задание 6
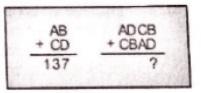
Ученик правильно сложил два двузначных числа, изображенных слева. Какой он должен получить ответ, если сложит числа, изображённые справа? Буквами обозначены цифры от 0 до 9.
Варианты ответов: (А) 13737; (Б) 13837; (В) 14747; (Г) 23737; (Д) 137137.
Наш вариант ответа: (Б) 13837
Задание 7
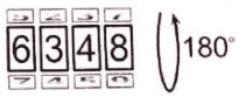
Велосипедный замок состоит из четырех вращающихся колесиков. На каждом колесике установлены цифры от 0 до 9. Переход от одной цифры к следующей или предыдущей получается поворотом колесика на 180 градусов против или по часовой стрелке соответственно. Какой код был установлен на замке велосипедистом, если сейчас на нём код 6348?
Варианты ответов: (А) 0815; (Б) 1893; (В) 1972; (Г) 4892; (Д) 8436.
Наш вариант ответа: (Б) 1893
Задание 8
Боря на 5 см выше Антона, но на 10 см ниже Вани. Гриша на 10 см выше Вани, но на 5 см ниже Димы. Какие из следующих утверждений верно?
(А) Антон и Дима одного роста;
(Б) Антон на 10 см выше Димы;
(В) Антон на 10 см ниже Димы;
(Г) Антон на 30 см выше Димы;
(Д) Антон на 30 см ниже Димы.
Наш вариант ответа: (Д) Антон на 30 см ниже Димы
Задания на 4 балла
Задание 9
Прямоугольная плитка шоколада состоит из равных квадратов. Нил отламывает две полные полосы квадратов и съедает полученные 12 квадратов. Позже Джек отрывает одну полную полосу квадратов от той же плитки и съедает 9 полученных квадратов. Сколько кусочков шоколада осталось в плитке?
Варианты ответов: (А) 72; (Б) 63; (В) 54; (Г) 45; (Д) 36.
Наш вариант ответа: (Г) 45
Задание 10
Банка, заполненная водой на пятую часть, весит 560 г. Та же банка, заполненная на четыре пятых водой, весит 740 г. Какой вес у пустой банки?
Варианты ответов: (А) 60 г; (Б) 112 г; (В) 180 г; (Г) 300 г; (Д) 500 г.
Наш вариант ответа: (Д) 500 г
Задание 11
Площадь большого квадрата 16 см², а площадь каждого маленького 1 см². Какая общая площадь черной фигуры?
Варианты ответов: (А) 3 см; (Б) 3,5 см; (В) 4; (Г) 5,5; (Д) 6.
Наш вариант ответа: (В) 4
Задание 12
5 квадратов расположены, как показано на рисунке. Площадь маленького квадрата равна 1. Чему равно h?
Варианты ответов: (А) 3; (Б) 3,5; (В) 4; (Г) 4,2; (Д) 4,5.
Наш вариант ответа: (В) 4
Задание 13
В викторине 20 вопросов. Каждый правильный ответ оценивается в 7 баллов, при каждом неправильном ответе списывается 4 балла. Если на вопрос не был дан ответ, то количество баллов не меняется. Саша за участие в викторине получил 100 баллов. На сколько вопросов он не ответил?
Варианты ответов: (А) 0; (Б) 1; (В) 2; (Г) 3; (Д) 4.
Наш вариант ответа: (Д) 4
Задание 14
Прямоугольную полоску бумаги 4 х 13 складывают, как показано на схеме.
У двух полученных прямоугольников площади равны P и Q, где P = 2Q. Чему равно х?
Варианты ответов: (А) 5; (Б) 5,5; (В) 6; (Г) 6,5; (Д) 4/2.
Наш вариант ответа: (В) 6
Задание 15
В коробке с фруктами в два раза больше яблок, чем груш. Кристи и Лили разделили их так, чтобы у Кристи было в два раза больше фруктов, чем у Лили. Какое из следующих утверждении всегда верно?
Варианты ответов:
(A) Кристи получила по крайней мере одну грушу
(Б) Кристи получила в два раза больше яблок чем груш
(B) Кристи получила вдвое больше яблок, чем Лили
(Г) у Кристи столько яблок, сколько у Лили груш
(Д) у Кристи было столько груш, сколько яблок у Лили
Наш вариант ответа: (Б) Кристи получила в два раза больше яблок чем груш
Задание 16
У обыкновенной дроби числитель и знаменатель положительны. Числитель этой дроби увеличен на 40 %. На какой процент следует уменьшить ее знаменатель, чтобы новая дробь была вдвое больше исходной дроби?
Варианты ответов: (А) 10%; (Б) 20%; (В) 30%; (Г) 40%; (Д) 50%.
Наш вариант ответа: (А) 10%
Задание 17
На рисунке справа показана пирамида построенная из 20 пушечных ядер. Какое пушечное ядро помечено одной из букв A,B,C,D или E. Имеются четыре пушечных ядра с метками каждого типа. На картинках внизу показаны надписи на ядрах на трёх гранях пирамиды. Какая метка на спрятанном ядре в центре четвёртой грани?
Варианты ответов: (А) A; (Б) B; (В) C; (Г) D; (Д) E.
Наш вариант ответа: (Г) D
Задание 18
Шестизначное число 1ABCDE умножается на 3 и в результате получается шестизначное ABCDE1. Какова сумма цифр этого числа?
Варианты ответов: (А) 24; (Б) 27; (В) 30; (Г) 33; (Д) 36.
Наш вариант ответа: (Б) 27
Задание 19
В коробке находятся только зеленые, красные, синие и желтые фишки. Среди любых 27 фишек, выбранных из коробки, всегда есть хотя бы одна зеленая фишка. Среди любых 25 фишек есть хотя бы одна красная. Среди 22 фишек есть хотя бы одна синяя. И всегда среди любых 17 фишек есть одна желтая. Какое наибольшее количество фишек может быть в коробке?
Варианты ответов: (А) 27; (Б) 29; (В) 51; (Г) 87; (Д) 91.
Наш вариант ответа: (Г) 87
Задание 20
Поверхность футбольного мяча состоит из белых шестиугольников и черных пятиугольников, как показано на рисунке. Всего имеется 12 пятиугольников. Сколько всего шестиугольников?
Варианты ответов: (А) 12; (Б) 15; (В) 18; (Г) 20; (Д) 24.
Наш вариант ответа: (Д) 24
Задание 21
У кубика Рубика 5*5*5 покрасили грани, а потом его распилили на единичные кубики. У скольких маленьких кубиков покрашена хотя бы одна грань?
Варианты ответов: (А) 96; (Б) 98; (В) 100; (Г) 120; (Д) 124.
Наш вариант ответа: (Б) 98
Задание 22
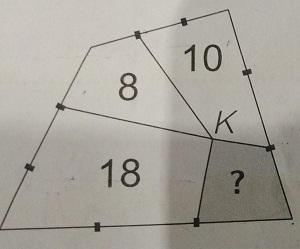
На схеме показан четырехугольник, разделенный на четыре меньших четырехугольника с общей вершиной К. Все стороны большого четырехугольника разделены на три равные части. Числами 8, 10 и 18 обозначены площади соответствующих маленьких четырехугольников. Какова площадь заштрихованного четырехугольника?
Варианты ответов: (А) 4; (Б) 5; (В) 6; (Г) 6,5; (Д) 7.
Наш вариант ответа: (А) 4
Задание 23
В городе 21 рыцарь, которые всегда говорят правду и 2000 лжецов, которые всегда лгут. Волшебник разделил 2020 из этих 2021 человек на 1010 пар. Каждый человек в паре описывал другого человека как рыцаря или лжеца. В результате 2000 человек были названы рыцарями, а 20 человек — лжецами. Сколько было пар из двух лжецов?
Варианты ответов: (А) 980; (Б) 985; (В) 990; (Г) 995; (Д) 1000.
Наш вариант ответа: (В) 990
Задание 24
Пять одинаковых прямоугольных треугольников можно расположить так, чтобы их большие острые углы соприкасались, образуя звезду, показанную на картинке. Также возможно сформировать другую звезду, расположив больше этих треугольников так, чтобы их меньшие острые углы соприкасались. Сколько треугольников нужно, чтобы образовалась вторая звезда?
Варианты ответов: (А) 10; (Б) 12; (В) 18; (Г) 20; (Д) 24.
Наш вариант ответа: (Г) 20
с 18 по 23 января 2021 года уже проводилась Олимпиада Кенгуру для выпускных 4, 9 и 11 класса
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

ГДЗ по математике 2 класс учебник Рудницкая, Юдачева часть 2 Страница 4-15
| 17.10.2021, 14:00 |
Страница 4
1. Сколько всего здесь рублей?
Как решил задачу Волк и как — Заяц? Кто из них быстрее справился с заданием? Почему?
Ответ:
Волк решил так:
1. сложил одну пятирублевую монету с второй пятирублевой монетой.
2. сумму двух пятирублевых монет сложил с третьей пятирублевой монетой.
3. сумму трех пятирублевых монет сложил с четвертой пятирублевой монетой.
4. сумму четырех пятирублевых монет сложил с пятой пятирублевой монетой.
5. сумму пяти пятирублевых монет сложил с шестой пятирублевой монетой.
5 + 5 = 10 рублей — сумма двух пятирублевых монет
10 + 5 = 15 рублей — сумма трех пятирублевых монет
15 + 5 = 20 рублей — сумма четырех пятирублевых монет
20 + 5 = 25 рублей — сумма пяти пятирублевых монет
25 + 5 = 30 рублей — сумма шести пятирублевых монет
Заяц умножил пятирублевую монету на количество таких монет.
5 • 6 = 30 рублей — сумма шести пятирублевых монет
Поэтому Заяц справился с заданием быстрее, чем волк.
Страница 5
2. Как найти результаты умножения чисел?
5 • 2 5 • 5
Ответ:
Нужно количество фишек в одном ряду умножить на количество рядов.
На 1 рисунке: 5 фишек в одном ряду нужно умножить на 2 ряда и получится 10 фишек. (5 • 2 = 10)
На 2 рисунке: 5 фишек в одном ряду нужно умножить на 5 рядов и получится 25 фишек. (5 • 5 = 25)
3. Вычисли, используя таблицу умножения.
5 • 3 5 • 4 5 • 9 5 • 2
5 • 7 5 • 1 5 • 6 5 • 8
Ответ:
5 • 3 = 15
5 • 7 = 35
5 • 4 = 20
5 • 1 = 5
5 • 9 = 45
5 • 6 = 30
5 • 2 = 10
5 • 8 = 40
4. Сравни результаты умножения.
5 • 2 и 2 • 5 5 • 3 и 3 • 5
5 • 4 и 4 • 5 5 • 1 и 1 • 5
Сделай вывод.
Ответ:
5 • 2 = 10 2 • 5 = 10
5 • 4 = 20 4 • 5 = 20
5 • 3 = 15 3 • 5 = 15
5 • 1 = 5 1 • 5 = 5
Можно сделать вывод, что от перемены мест множителей произведение не меняется.
5. Умножь 5 на 0, 0 на 5. Какое число получилось?
Ответ:
5 • 0 = 0
0 • 5 = 0
При умножении любого числа на 0 или 0 на любое число получится 0.
6. Используя таблицу умножения числа 5, составь и запиши таблицу умножения на число 5.
Назови результаты умножения.
3 • 5 7 • 5 6 • 5 5 • 5
Ответ:
5 • 1 = 5
5 • 2 = 10
5 • 3 = 15
5 • 4 = 20
5 • 5 = 25
5 • 6 = 30
5 • 7 = 35
5 • 8 = 40
5 • 9 = 45
5 • 10 = 50
3 • 5 = 15
7 • 5 = 35
6 • 5 = 30
5 • 5 = 25
7. На сколько квадратов разделена каждая фигура? Реши задачу разными способами. Каким способом можно подсчитать число квадратов быстрее?
Ответ:
Желтая фигура
1 способ: 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 = 14 квадратов
2 способ: (4 + 4) + (3 + 3) = 8 + 6 = 14 квадратов
3 способ: (5 + 5) + (2 + 2) = 10 + 4 = 14 квадратов
4 способ: (4 • 2) + (3 • 2) = 8 + 6 = 14 квадратов
5 способ: (5 • 2) + (2 • 2) = 10 + 4 = 14 квадратов
Вывод: быстрее считать 2, 3, 4 и 5 способом.
Синяя фигура
1 способ: 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 = 17 квадратов
2 способ: (1 + 1) + (5 + 5 + 5) = 2 + 15 = 17 квадратов
3 способ: (3 + 3 + 3 + 3 + 3) + (1 + 1) = 15 + 2 = 17 квадратов
4 способ: (3 + 3 + 3 + 3) + 5 = 12 + 5 = 17 квадратов
5 способ: (1 • 2) + (5 • 3) = 2 + 15 = 17 квадратов
6 способ: (3 • 4) + 5 = 12 + 5 = 17 квадратов
7 способ: (3 • 5) + (1 + 1) = 15 + 2 = 17 квадратов
Вывод: быстрее считать 6 способом.
Страница 6
8. Туристы разбили лагерь и поселились по 3 человека в палатке. Рассмотри рисунок и ответь: сколько всего человек живёт в лагере? Какими данными нужно дополнить текст задачи, чтобы её можно было решить без рисунка?
Составь полный текст задачи и реши её.
Ответ:
3 + 3 + 3 + 3 + 3 = 15 человек — всего живет в лагере
Не хватает количество палаток — 5.
Туристы разбили лагерь и поселились по 3 человека в палатке. Всего поставили 5 палаток. Сколько всего человек живёт в лагере?
5 • 3 = 15 человек — всего живет в лагере
9. В пруду плавают 3 утки, у каждой 5 утят. Сколько всего птиц плавает в пруду?
Ответ:
3 • 5 = 15 птиц — всего
10. Измерь длины сторон пятиугольников и вычисли периметр каждого.
Ответ:
Зеленый пятиугольник: все стороны = 2 см.
2 + 2 + 2 + 2 + 2 =10 см — периметр
Синий пятиугольник: три стороны = 3 см и две стороны = 2 см.
3 + 3 + 3 + 2 + 2 = 13 см — периметр
11. Вычисли.
(36 : 4) • 5 (5 • 7) — 35
(91 — 63) : 4 (97 — 89) • 5
(5 • 5) + 47 (7 • 5) — 26
100 — (52 + 48) 8 • (100 — 95)
(32 : 4) + 76 (28 : 4) + 93
Ответ:
(36 : 4) • 5 = 9 • 5 = 45
(91 — 63) : 4 = 28 : 4 = 7
(5 • 5) + 47 = 25 + 47 = 72
100 — (52 + 48) = 100 — 100 = 0
(32 : 4) + 76 = 8 + 76 = 84
(5 • 7) — 35 =35 — 35 = 0
(97 — 89) • 5 = 8 • 5 = 40
(7 • 5) — 26 = 35 — 26 = 9
8 • (100 — 95) = 8 • 5 = 40
(28 : 4) + 93 = 7 + 93 = 100
Страница 7
12. Используя таблицу умножения на 5, выполни деление.
35 : 5 5 : 5 30 : 5 25 : 5
15 : 5 10 : 5 45 : 5 40 : 5
Ответ:
35 : 5 = 7
15 : 5 = 3
5 : 5 = 1
10 : 5 = 2
30 : 5 = 6
45 : 5 = 9
25 : 5 = 5
40 : 5 = 8
13. Вычисли.
5 • 5 20 : 5 9 • 5 2 • 5
18 : 3 0 • 5 1 • 5 36 : 4
Ответ:
5 • 5 = 25
18 : 3 = 6
20 : 5 = 4
0 • 5 = 0
9 • 5 = 45
1 • 5 = 5
2 • 5 = 10
36 : 4 = 9
14. Умножь 0 на 5, результат раздели на 5. Какое число получилось? Объясни свой ответ.
Ответ:
0 • 5 = 0 0 : 5 = 0
При умножении или делении 0 на любое число получится 0.
15. Выполни действия. В каких примерах без выполнения указанных вычислений можно сразу назвать результат? Обоснуй свой ответ.
(16 : 4) • 4 45 + (25 : 5) (90 — 45) : 5
(4 • 4) : 4 61 — (4 • 7) 5 • (74 — 63)
(35 : 5) • 3 (30 : 5) + 54 (17 + 23) : 5
(6 • 5) • 0 0 • (45 : 5) 5 • (12 : 4)
Ответ:
Можно сразу назвать результат в таких примерах как:
1) (16 : 4) • 4 — потому что сначала делим, а затем умножаем на одно и то же число.
2) (4 • 4) : 4 — потому что сначала умножаем, а затем делим на одно и то же число.
3) (6 • 5) • 0 — потому что при умножении любого числа на 0 получится 0.
4) 0 • (45 : 5) — потому что при умножении 0 на любое число получится 0.
(16 : 4) • 4 = 4 • 4 = 16
(4 • 4) : 4 = 16 : 4 = 4
(35 : 5) • 3 = 7 • 3 = 21
(6 • 5) • 0 = 30 • 0 = 0
45 + (25 : 5) = 45 + 5 = 50
61 — (4 • 7) = 61 — 28 = 33
(30 : 5) + 54 = 6 + 54 = 60
0 • (45 : 5) = 0 • 9 = 0
(90 — 45) : 5 = 45 : 5 = 9
5 • (74 — 63) = 5 • 11 = 55
(17 + 23) : 5 = 40 : 5 = 8
5 • (12 : 4) = 5 • 3 = 15
16. В пяти клетках разместили поровну 20 хомячков. Сколько хомячков оказалось: в одной клетке; в трёх клетках?
Ответ:
1) 20 : 5 = 4 хомячка — в одной клетке
2) 5 • 3 = 15 хомячков — в трех клетках
Страница 8
17. В альбом наклеили 30 фотографий, по 5 на страницу. Сколько страниц альбома заняли эти фотографии? Сколько страниц заняли 15 фотографий?
Ответ:
1) 30 : 5 = 6 страниц — заняли 30 фотографий
2) 15 : 5 = 3 страницы — заняли 15 фотографий
18. На 5 одинаковых шапочек израсходовали 15 мотков пряжи. Сколько мотков пряжи пошло на изготовление двух шапочек; четырёх шапочек? Сколько мотков пряжи нужно, чтобы изготовить 6 шапочек; 7 шапочек; 9 шапочек?
Ответ:
1) 15 : 5 = 3 мотка — пряжи пошло на изготовление одной шапочки
2) 3 • 2 = 6 мотков — пряжи пошло на изготовление двух шапочек
3) 3 • 4 = 12 мотков — пряжи пошло на изготовление четырех шапочек
4) 3 • 6 = 18 мотков — пряжи нужно, чтобы изготовить 6 шапочек
5) 3 • 7 = 21 моток — пряжи нужно, чтобы изготовить 7 шапочек
6) 3 • 9 = 27 мотков — пряжи нужно, чтобы изготовить 9 шапочек
19. Пряники разложили поровну в 6 коробок. В пяти коробках — 45 штук. Сколько пряников в шестой коробке?
Ответ:
1) 45 : 5 = 9 пряников — в одной коробке
2) 9 • 6 = 54 пряника — в шести коробках
3) 54 — 45 = 9 пряников — в шестой коробке
20. Художник расписал 30 подносов за 5 дней. Ежедневно он расписывал одно и то же число подносов.
В следующие дни он стал расписывать на 3 подноса в день больше. Сколько подносов он стал расписывать ежедневно?
Ответ:
1) 30 : 5 = 6 подносов — художник расписывал в день
2) 6 + 3 = 9 подносов — художник стал расписывать ежедневно
21. Найди пятую часть чисел: 10, 40, 35, 20, 25.
Ответ:
10 : 5 = 2
40 : 5 = 8
35 : 5 = 7
20 : 5 = 4
25 : 5 = 5
Страница 9
22. Длина отрезка равна 3 дм 5 см. Какова длина его пятой части? В каких единицах надо записать длину отрезка, чтобы ответить на вопрос задачи?
Ответ:
Чтобы решить задачу, нужно длину перевести в одинаковые единицы измерения (в сантиметры).
3 дм 5 см = 35 см
35 : 5 = 7 см — длина пятой части отрезка
23. Миша поймал 6 рыб утром и 4 вечером. Пятую часть улова он отдал кошке, остальную рыбу пожарили. Сколько рыб досталось кошке и сколько рыб пожарили?
Ответ:
1) 6 + 4 = 10 рыб — Миша поймал всего
2) 10 : 5 = 2 рыбы — Миша отдал кошке
3) 10 — 2 = 8 рыб — пожарили
24. Пятая часть числа равна 8. Какое это число?
Ответ:
8 • 5 = 40
Проверка: 40 : 5 = 8
25. Длина пятой части верёвки равна 9 м. Найди длину всей верёвки.
Ответ:
9 • 5 = 45 см — длина всей веревки
26. Какая часть круга закрашена?
Ответ:
1) пятая часть, т.е. одна пятая (1/5)
2) две пятых (2/5)
3) три пятых (3/5)
4) четыре пятых (4/5)
Страница 10
27. Начерти квадрат с длиной стороны 5 см. Расскажи, как ты будешь выполнять чертёж: с чего начнёшь, что будешь делать потом. Раскрась пятую часть квадрата.
Ответ:
Нужно взять линейку и карандаш, отмерить на линейке 5 см и начертить горизонтальную линию, затем от конца этой линии отмерить 5 см вниз и начертить вертикальную линию. Далее от конца этой линии нужно отмерить 5 см влево и провести горизонтальную линию и в конце соединить конец этой линии с началом первой линии.
У вас получится квадрат.
Затем нужно квадрат разделить на 5 равных частей: для этого нужно провести вертикально или горизонтально четыре линии, найти пятую часть квадрата и раскрасить ее.
5 частей квадрата : 5 = 1 — пятая часть квадрата
Как ты понимаешь пословицу?
«Человека узнаешь, когда с ним пуд соли съешь».
Ответ:
Задача 1. Крестьянин обмолотил 2 копны ржи и с каждой копны получил 5 пудов зерна. Сколько всего пудов зерна получил крестьянин? Сколько примерно килограммов зерна получил крестьянин с каждой копны ржи?
Вычисления выполни на калькуляторе.
Ответ:
1) 2 • 5 = 10 пудов — зерна крестьянин получил всего
2) 1 пуд = 16 кг
16 • 10 = 160 кг — зерна крестьянин получил с каждой копны ржи
Задача 2. Мальчик поменял 4 медных пятака на одну серебряную монету. Какая это монета? (Во сколько копеек?)
Ответ:
медный пятак — это 5 копеек
4 • 5 = 20 копеек
Серебряная монета — это 20 копеек
Страница 11
28. Используя таблицу умножения, умножь на число 4 числа: 1, 3, 5, 7, 9.
Ответ:
1 • 4 = 4
3 • 4 = 12
5 • 4 = 20
7 • 4 = 28
9 • 4 = 36
29. Каждое из чисел 16, 24, 8, 32, 36 раздели на 4.
Ответ:
16 : 4 = 4
24 : 4 = 6
8 : 4 = 2
32 : 4 = 8
36 : 4 = 9
30. Найди треть чисел: 18, 27, 21.
Ответ:
18 : 3 = 6
27 : 3 = 9
21 : 3 = 7
31. Запишите только ответы в два столбика.
40 + 30 (6 • 2) : 4
60 — 50 (32 : 4) • 3
50 + 50 (15 + 9) : 3
30 — 30 (10 — 2) • 4
40 + 5 2 • (12 : 3)
40 — 5 24 : (16 : 4)
31 + 9 8 • (20 — 16)
42 + 8 0 • (54 — 49)
Поменяйтесь тетрадями и проверьте ответы друг у друга.
Ответ:
40 + 30 = 70 (6 • 2) : 4 = 3
60 — 50 = 10 (32 : 4) • 3 = 24
50 + 50 = 100 (15 + 9) : 3 = 8
30 — 30 = 0 (10 — 2) • 4 = 32
40 + 5 = 45 2 • (12 : 3) = 8
40 — 5 = 35 24 : (16 : 4) = 6
31 + 9 = 40 8 • (20 — 16) = 32
42 + 8 = 50 0 • (54 — 49) = 0
32. Выполни действия.
(53 — 29) + 16 (33 — 6) — 12
(96 + 4) — 38 100 — (90 — 45)
(26 + 48) + 19 37 + (61 — 19)
(54 + 46) — 54 81 — (57 + 3)
(47 — 13) + 47 (56 + 9) — 18
Выпиши результаты действий в порядке увеличения.
Ответ:
(53 — 29) + 16 = 24 + 16 = 40
(96 + 4) — 38 = 100 — 38 = 62
(26 + 48) + 19 = 74 + 19 = 93
(54 + 46) — 54 = 100 — 54 = 46
(47 — 13) + 47 = 34 + 47 = 81
(33 — 6) — 12 = 27 — 12 = 15
100 — (90 — 45) = 100 — 45 = 55
37 + (61 — 19) = 37 + 42 = 79
81 — (57 + 3) = 81 — 60 = 21
(56 + 9) — 18 = 65 — 18 = 47
Результаты действий в порядке увеличения: 15; 21; 40; 46; 47; 55; 62; 79; 81; 93.
33. Сложили два числа и получили 32. Какие это числа, если сумма больше одного из чисел на 20?
Ответ:
32 — 20 = 12 — первое слагаемое
32 — 12 = 20 — второе слагаемое
Проверка: 12 + 20 = 32
Страница 12
34. Число умножили на 4 и получили 36. Какое это число?
Ответ:
36 : 4 = 9
Проверка: 9 • 4 = 36
Это число 9.
35. Число разделили на 4 и получили 7. Какое это число?
Ответ:
7 • 4 = 28
Проверка: 28 : 4 = 7
Это число 28.
36. На тарелке лежат яблоко, груша и апельсин. Надо взять один фрукт. Укажи все варианты. Сколько их?
Реши аналогичную задачу, изменив число выбираемых плодов: 2 плода, 3 плода. Рассмотри все варианты решения.
Ответ:
Вариант 1. Взяли яблоко.
Вариант 2. Взяли грушу.
Вариант 3. Взяли апельсин.
Если нужно взять один фрукт, то вариантов — 3.
На тарелке лежат яблоко, груша и апельсин. Надо взять два фрукта. Укажи все варианты. Сколько их?
Вариант 1. Взяли яблоко и грушу.
Вариант 2. Взяли грушу и апельсин.
Вариант 3. Взяли апельсин и яблоко.
Если нужно взять два фрукта, то вариантов — 3.
На тарелке лежат яблоко, груша и апельсин. Надо взять три фрукта. Укажи все варианты. Сколько их?
Вариант 1. Взяли яблоко, грушу и апельсин.
Если нужно взять три фрукта, то вариантов — 1.
37. Какое время будут показывать часы: через час; через 1 ч 20 мин? Какое время показывали часы 10 минут назад?
Ответ:
а) Часы показывают 7 часов.
Через час они будут показывать: 7 ч + 1 ч = 8 ч
Через 1 ч 20 мин они будут показывать: 7 ч + 1 ч 20 мин = 8 ч 20 мин
10 минут назад часы показывали: 7 ч можно представить как 6 ч 60 мин
6 ч 60 мин — 10 мин = 6 ч 50 мин
б) Часы показывают 12 часов.
Через час они будут показывать: 12 ч + 1 ч = 13 ч
Через 1 ч 20 мин они будут показывать: 12 ч + 1 ч 20 мин = 13 ч 20 мин
10 минут назад часы показывали: 12 ч можно представить как 11 ч 60 мин
11 ч 60 мин — 10 мин = 11 ч 50 мин
Страница 13
38. Рассмотри фигуры.
Дай общее название всем фигурам. Распредели фигуры на группы так, чтобы в каждой были фигуры с равным числом сторон. Сколько групп получилось? Дай общее название фигурам в каждой группе.
Ответ:
Фигуры — многоугольники.
1 группа: 1 и 3 фигуры.
2 группа: 2 и 4 фигуры.
Получилось 2 группы.
1 группа: четырехугольники.
2 группа: пятиугольники.
39. Какие числа написаны:
в пятиугольнике;
в круге, но не в треугольнике;
в четырёхугольнике, но не в круге;
в треугольнике и пятиугольнике;
в четырёхугольнике и круге;
в треугольнике, пятиугольнике и круге?
Ответ:
В пятиугольнике: 65; 33; 48; 9; 100.
В круге, но не в треугольнике: 27; 50; 100.
В четырёхугольнике, но не в круге: 33; 48.
В треугольнике и пятиугольнике: 65; 9; 33; 48; 100.
В четырёхугольнике и круге: 33; 48; 100; 9; 27; 50.
В треугольнике, пятиугольнике и круге: 65; 9; 33; 48; 100; 27; 50.
Страница 14
40. В корзине лежат яблоки, груши и лимоны. Яблок — 10. Груш — на 2 больше, чем яблок. Лимонов — на 3 больше, чем груш. На сколько лимонов больше, чем яблок? Реши задачу, выполнив только одно действие. Какое данное при этом в условии задачи окажется лишним?
Ответ:
2 + 3 = 5 лимонов больше, чем яблок
Количество яблок является лишним данным в условии задачи.
Видео:Математика это не ИсламСкачать

Четырехугольники
теория по математике 📈 планиметрия
Четырехугольник – это геометрическая фигура, состоящая из четырех точек, никакие три из которых не лежат на одной прямой, и отрезков, последовательно соединяющих эти точки.
Выпуклый четырехугольник
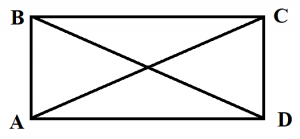
Четырехугольник называется выпуклым, если он находится в одной полуплоскости (то есть все его стороны расположены только с одной стороны прямой, прямая НЕ разбивает фигуру) относительно прямой, содержащей любую его сторону. На рисунке показан выпуклый четырехугольник АВСD.

Диагональ четырехугольника – отрезок, соединяющий любые две не соседние вершины. На рисунке 2 диагоналями являются отрезки АС и BD.
Видео:ЧТО НАДО ГОВОРИТЬ ЕСЛИ НЕ СДЕЛАЛ ДОМАШКУ!Скачать

Виды и свойства выпуклых четырехугольников
Сумма углов выпуклого четырехугольника равна 360 градусов.
Прямоугольник
Прямоугольник – это четырехугольник, у которого все углы прямые.

- Противоположные стороны прямоугольника равны (АВ=CD, ВС=АD).
- Диагонали прямоугольника равны (АС=ВD).
- Диагонали пересекаются и точкой пересечения делятся пополам.
- Периметр прямоугольника – это сумма длин всех сторон: Р=(а + b) × 2, где а и b соседние (смежные) стороны прямоугольника
- Площадь прямоугольника – это произведение длин соседних (смежных) сторон, формула для нахождения площади прямоугольника:
S=ab, где a и b соседние стороны прямоугольника.
Квадрат
Квадрат – это прямоугольник, у которого все стороны равны.
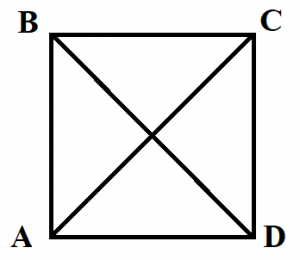
- Диагонали квадрата равны (BD=AC).
- Диагонали квадрата пересекаются под углом 90 градусов.
- Диагонали квадрата точкой пересечения делятся пополам (BO=OD, AO=OC).
- Периметр квадрата – это сумма длин всех сторон. Так как все стороны квадрата равны, то его можно найти по формуле Р=4×а, где а — длина стороны квадрата.
- Площадь квадрата – это произведение длин соседних сторон, формула для нахождения площади прямоугольника S=a 2 , где a — длина стороны квадрата.
Параллелограмм
Параллелограмм – это четырехугольник, у которого противоположные стороны попарно параллельны.
Ромб – это параллелограмм, у которого все стороны равны.
Трапеция
Трапеция – это четырехугольник, у которого только две противоположные стороны параллельны. Параллельные стороны называются основаниями трапеции, а две другие стороны – боковыми сторонами трапеции.
Виды трапеций
Трапеция называется прямоугольной, если у нее боковая сторона перпендикулярна основаниям. Прямоугольная трапеция имеет два прямых угла.
углы А и С равны по 90 градусов
Средняя линия трапеции
Сделаем чертеж параллелограмма и покажем на нем биссектрисы углов, которые пересекаются в точке N.
Угол ANB равен углу NАD как накрест лежащие при параллельных прямых ВС и АD и секущей AN. А по условию углы BАN и NАD равны (AN биссектриса). Следовательно, углы BАN и BNА равны. Значит, треугольник ABN является равнобедренным, у него АВ= BN.
Аналогично, через равенство углов CND, ADN и CDN доказывается, что треугольник CND является равнобедренным, у него CN=DC.
По условию задачи мы имеем параллелограмм, а по свойству параллелограмма – противолежащие стороны равны, т.е. АВ=СD, значит, АВ=BN=NC=CD. Таким образом, мы доказали, что BN=NC, т.е. N – середина ВС.
Ответ: см. решение
pазбирался: Даниил Романович | обсудить разбор | оценить
Найдите боковую сторону АВ трапеции ABCD, если углы АВС и BCD равны соответственно 30 0 и 135 0 , а СD =17
Сделаем чертеж, выполнив на нём дополнительные построения – высоты АМ и СН, которые равны как расстояния между параллельными сторонами трапеции.
Рассмотрим треугольник CНD, где CD=17, угол Н=90 0 , следовательно, треугольник прямоугольный. Найдем величину угла DCН, 135 0 – 90 0 =45 0 (так как провели высоту CН). Отсюда следует, что угол D=45 0 , так как треугольник прямоугольный. Значит, треугольник является равнобедренным (углы D и DCН равны по 45 градусов).
Найдем катеты CН и DН по теореме Пифагора, как катет равнобедренного треугольника по формуле с=а √ 2 , где с=17. Следовательно, CН = 17 √ 2 . . = 17 √ 2 2 . . .
Рассмотрим прямоугольный треугольник АВМ, где угол В равен 30 градусов, а катет АМ= CН= 17 √ 2 2 . . . Зная, что катет, лежащий напротив угла в 30 градусов, равен половине гипотенузы, найдем АВ (она будет в два раза больше катета). АВ=2 × 17 √ 2 2 . . =17 √ 2
Ответ: см. решение
pазбирался: Даниил Романович | обсудить разбор | оценить
Основания трапеции равны 7 и 11, а высота равна 7. Найти площадь этой трапеции.
Для нахождения площади трапеции в справочном материале есть формула
S = a + b 2 . . h , для которой у нас известны и основания, и высота. Подставим в неё эти значения и вычислим: S = 7 + 11 2 . . ∙ 7 = 18 2 . . ∙ 7 = 9 ∙ 7 = 63
pазбирался: Даниил Романович | обсудить разбор | оценить
Радиус вписанной в квадрат окружности равен 22 √ 2 . Найти диагональ этого квадрата.
Для начала надо сделать построения на чертеже, чтобы увидеть, как располагаются известные и неизвестные элементы и чем они еще могут являться на чертеже.
Обозначим диагональ АВ, точкой О – центр окружности, С – один из углов квадрата. Покажем расстояние от центра окружности до стороны квадрата – радиус r. Если радиус равен 22 √ 2 , то сторона квадрата будет в два раза больше, т.е. 44 √ 2 .
Рассмотрим прямоугольный треугольник АВС, который является равнобедренным (так как по условию дан квадрат) и боковые стороны равны по 44 √ 2 . Нам надо найти диагональ, т.е. гипотенузу данного треугольника. Вспомним, что для нахождения гипотенузы равнобедренного треугольника есть формула с=а √ 2 , где с – гипотенуза, а – катет. Подставим в неё наши данные:
с=44 √ 2 × √ 2 =44 √ 4 =44 × 2=88
pазбирался: Даниил Романович | обсудить разбор | оценить
Площадь четырехугольника можно вычислить по формуле S= d 1 d 2 s i n a 2 . . , где d 1 и d 2 длины диагоналей четырехугольника, а – угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали d 1 , если d 2 =16, sin a= 2 5 . . , a S=12,8
Для выполнения данного задания надо подставить все известные данные в формулу:
12,8= d 1 × 16 × 2 5 . . 2 . .
В правой части можно сократить 16 и 2 на 2: 12,8= d 1 × 8 × 2 5 . . 1 . .
Теперь умножим 8 на дробь 2 5 . . , получим 3,2: 12,8= d 1 × 3 , 2
Найдем неизвестный множитель, разделив 12,8 на 3,2: d 1 =12,8:3,2=4
pазбирался: Даниил Романович | обсудить разбор | оценить
На плане изображен дачный участок по адресу: п. Сосновка, ул. Зеленая, д. 19 (сторона каждой клетки на плане равна 2 м). Участок имеет прямоугольную форму. Выезд и въезд осуществляются через единственные ворота.
При входе на участок слева от ворот находится гараж. Справа от ворот находится сарай площадью 24 кв.м, а чуть подальше – жилой дом. Напротив жилого дома расположены яблоневые посадки. Также на участке есть баня, к которой ведет дорожка, выложенная плиткой, и огород с теплицей внутри (огород отмечен на плане цифрой 6). Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1м х 1м. Между гаражом и сараем находится площадка, вымощенная такой же плиткой. К участку подведено электричество. Имеется магистральное газоснабжение.
Задание №1
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в бланк ответов перенесите последовательность четырех цифр без пробелов, запятых и других символов.
| Объекты | яблони | теплица | сарай | жилой дом |
| Цифры |
Решение
Для решения 1 задачи работаем с текстом и планом одновременно:
при входе на участок слева от ворот находится гараж (слева от входа находится объект под номером 2), итак, гараж — 2. Справа от ворот находится сарай площадью 24 кв.м (справа объект под номером 1), сарай – номер 1. А чуть подальше – жилой дом, следовательно, жилой дом – объект под номером 7. Напротив жилого дома расположены яблоневые посадки, на плане они обозначены цифрой 3. Также на участке есть баня, к которой ведет дорожка, выложенная плиткой, на плане видим, что к объекту под номером 4 ведет дорожка, значит баня – 4. Огород с теплицей внутри (огород отмечен на плане цифрой 6), в огороде расположена теплица – объект 5.
Итак, получили следующее:
1 – сарай; 2 – гараж; 3 – яблоневые посадки; 4 – баня; 5 – теплица; 6 – огород; 7 – жилой дом.
Заполняем нашу таблицу:
| Объекты | яблони | теплица | сарай | жилой дом |
| Цифры | 3 | 5 | 1 | 7 |
Записываем ответ: 3517
Задание №2
Плитки для садовых дорожек продаются в упаковках по 6 штук. Сколько упаковок плиток понадобилось, чтобы выложить все дорожки и площадку между сараем и гаражом?
Решение
Для начала надо определить, как обозначены дорожки, которые надо выложить плиткой, на плане. На плане они показаны серым цветом (мы их обведём голубым цветом).
Теперь ищем в условии задачи, что сказано про плитки и дорожки: «Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1м х 1м».
Сосчитаем, сколько клеточек (плиток) на плане, получаем 65. Зная по условию задачи 1, что плитки продаются в упаковках по 6 штук, разделим 65 на 6. Заметим, что 65 на 6 не делится, получается приблизительно 10,8…Учитывая, что упаковки не делятся, округляем до большего целого числа, нам понадобится 11 упаковок.
Задание №3
Найдите расстояние от жилого дома до теплицы (расстояние между двумя ближайшими точками по прямой) в метрах.
Решение
Из задания 1 знаем, что жилой дом обозначен на плане цифрой 7, а теплица цифрой 5. Следовательно, на плане находим эти объекты и расстояние между двумя ближайшими точками по прямой (обозначим это голубым цветом). Видим, что это расстояние – 2 клетки. На плане показано, что длина стороны одной клетки равна 2 метра, значит, расстояние между двумя этими объектами равно 4 метра.
Задание №4
Найдите площадь, которую занимает гараж. Ответ дайте в квадратных метрах.
Решение
Найдем на плане гараж, это объект под номером 2. Гараж имеет прямоугольную форму, следовательно, нам надо найти площадь прямоугольника. Для этого надо найти длину и ширину. На плане показано, что длина стороны 1 клетки равна 2 метра, значит, длина гаража равна 8 м (4 клетки), а ширина — 6 м (3 клетки).
Зная ширину и длину, находим площадь гаража: 6х8=48 кв.м
Задание №5
Хозяин участка решил покрасить весь забор вокруг участка (только с внешней стороны) в зелёный цвет. Площадь забора равна 232 кв.м., а купить краску можно в одном из двух ближайших магазинов. Цена и характеристика краски и стоимость доставки заказа даны в таблице.
| Номер магазина | Расход краски | Масса краски в одной банке | Стоимость одной банки краски | Стоимость доставки заказа |
| 1 | 0,25 кг/кв.м | 6 кг | 3000 руб. | 500 руб. |
| 2 | 0,4 кг/кв.м | 5 кг | 1900 руб. | 800 руб. |
Во сколько рублей обойдется наиболее дешёвый вариант покупки с доставкой?
Решение
Определим, сколько килограммов краски понадобится для покраски забора площадью 232 кв.м:
1 магазин: 232х0,25=58 кг
2 магазин: 232х0,4=92,8 кг
Вычислим количество банок краски, которое надо купить, зная массу краски в 1 банке:
1 магазин: 58:6=9,7…; так как банки продаются целиком, то надо 10 банок (округляем до наибольшего целого числа)
2 магазин: 92,8:5=18,56; значит надо 19 банок.
Вычислим стоимость краски в каждом магазине плюс доставка:
1 магазин: 10х3000+500=30500 руб.
2 магазин: 19х1900+800=36900 руб.
Из решения задачи видно, что в 1 магазине купить краску выгоднее. Следовательно, наиболее дешёвый вариант покупки с доставкой будет стоить 30500 рублей.
Ответ: см. решение
pазбирался: Даниил Романович | обсудить разбор | оценить
🔥 Видео
Я оплачу Все, что ты вместишь в этот ТреугольникСкачать

Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Я Оплачу Все, что Вы Вместите в Этот КругСкачать

Как правильно решить задание про четырёхугольник? / Разбор заданий на ОГЭ по геометрииСкачать

Площадь треугольника. Как найти площадь треугольника?Скачать

Площади фигур. Сохраняй и запоминай!#shortsСкачать

8 класс, 3 урок, ЧетырехугольникСкачать

Что такое угол? Виды углов: прямой, острый, тупой, развернутый уголСкачать

Эта Находка в Бермудском Треугольнике Испугала Всех УченыхСкачать

Сколько треугольников на рисунке? Универсальный алгоритм решения задачиСкачать
Задача, которую не решил на математическом Что? Где? Когда?Скачать

Задача на логику и сообразительность про яблоки и груши. Сможешь ли решить?Скачать

Что такое выпуклый четырёхугольник? | Математика 8 класс | Геометрия 8 класс | МегаШколаСкачать

КАК РЕШАТЬ ЗАДАЧИ ПО ГЕОМЕТРИИ? | МатематикаСкачать

Репетитор по математике. Доли. Нахождение доли от числаСкачать

Площадь круга. Математика 6 класс.Скачать