Как решить египетский треугольника

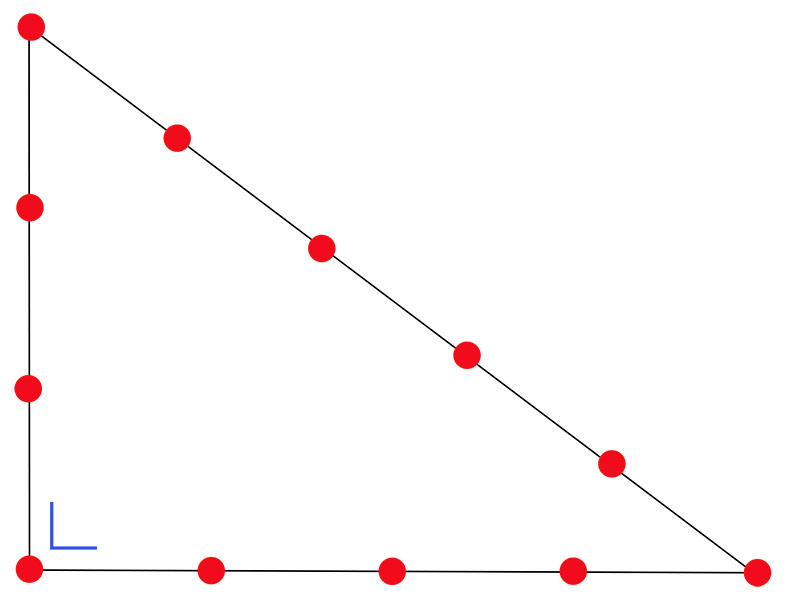
О египетском треугольнике и его свойствах хорошо известно ещё с древних времён. Эта фигура широко применялась в строительстве для разметки и построения правильных углов.

Видео:Египетский треугольник. Пифагоровы тройки.Скачать

История египетского треугольника

Создателем этой геометрической конструкции является один из величайших математиков древности Пифагор. Именно благодаря его математическим изысканиям мы можем в полной мере использовать все свойства данного геометрического построения в строительстве.

Можно предположить, что математические навыки позволили Пифагору заметить закономерность в формах строения. Дальнейшее развитие событий можно легко представить. Базовый анализ и построение выводов создали одну из самых значимых фигур в истории. Скорее всего, в качестве прообраза была выбрана именно пирамида Хеопса из-за своих практически совершенных пропорций.

Видео:Египетский треугольникСкачать

Египетский треугольник в строительстве

Свойства этой уникальной геометрической конструкции заключаются в том, что её построение без применения каких-либо инструментов позволяет построить дом с правильными во всех соотношениях углами.

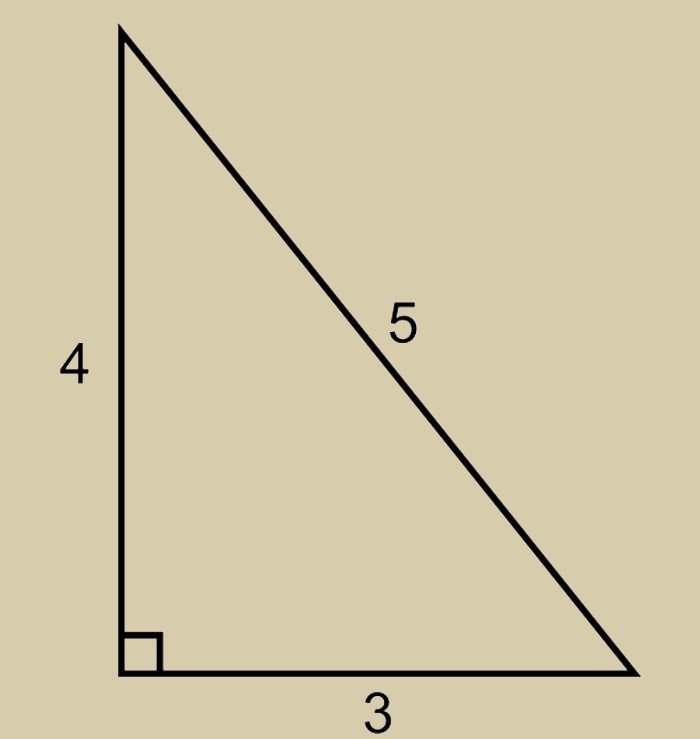
Итак, качества египетского треугольника позволяют делать правильные во всех соотношениях углы. Стороны конструкции имеют следующее соотношение друг к другу:

Чтобы проверить ту ли фигуру вы начертили, используйте хорошо известную ещё со школьной скамьи Теорему Пифагора.

Для лучшего понимания возьмём приведенную выше зависимость и составим небольшой пример. Умножим пять на пять. В результате чего получим гипотенузу равную 25. Вычислим квадраты двух катетов. Они составят 16 и 9. Соответственно их сумма будет двадцать пять.

Именно поэтому свойства египетского треугольника так часто используются в строительстве. Вам достаточно взять заготовку и прочертить прямую линию. Её длина всегда должна быть кратной 5. Затем нужно наметить один край и отмерять от него линию кратную 4, а от второго 3.

Альтернативные способы построить прямой угол на 90 градусов

Как уже упоминалось выше, наилучшим вариантом будет просто взять угольник или транспортир. Эти инструменты позволяют с наименьшими затратами времени и сил добиться нужных пропорций. Главное же свойство египетского треугольника заключается в его универсальности. Фигуру можно построить, не имея в арсенале практически ничего.

Сильно в построении прямого угла помогают простые печатные издания. Возьмите любой журнал или книгу. Дело в том, что в них соотношение сторон всегда составляет ровно 90 градусов. Типографические станки работают очень точно. В противном случае рулон, который заправляется в станок, будет резаться непропорциональными кривыми углами.

Как получить египетский треугольник при помощи верёвки

Свойства этой геометрической фигуры тяжело переоценить. Неудивительно, что инженерами древности было придумано множество способов её образования с использованием минимальных ресурсов.

Одним из самых простых считается метод образования египетского треугольника со всеми его вытекающими свойствами посредством простой верёвки. Возьмите бечёвку и разрежьте её на 12 абсолютно ровных частей. Из них сложите фигуру с пропорциями 3, 4 и 5.

Как построить угол в 45, 30 и 60 градусов

Безусловно, египетский треугольник и его свойства очень полезны при постройке дома. Но без других углов вам обойтись всё-таки не удастся. Чтобы получить угол, равняющийся 45 градусам, возьмите материал рамки или багета. После чего распилите его под углом в сорок пять градусов и состыкуйте половинки друг с другом.

Как видите, свойства фигуры позволяют гораздо проще и быстрее построить геометрический конструкт. Чтобы добиться соотношения сторон в 60 градусов нужно взять один треугольник на 30º и второй такой же. Обычно подобные пропорции необходимы при создании определённых декоративных элементов.

Видео:Египетский треугольник #огэ #математика #shortsСкачать

Итоги

Свойства египетского треугольника широко использовались в строительстве на протяжении почти, что двух с половиной веков. Даже сейчас при недостатке инструментов строители применяют эту открытую ещё Пифагором методику, чтобы добиться ровных прямых углов.

Видео:Пифагоровы тройки 1. Египетский треугольникСкачать

Египетский треугольник и обратная теорема Пифагора

Математический лайфхак из обасти геометрии “Как при помощи простой верёвки получить треугольник с прямым углом”.
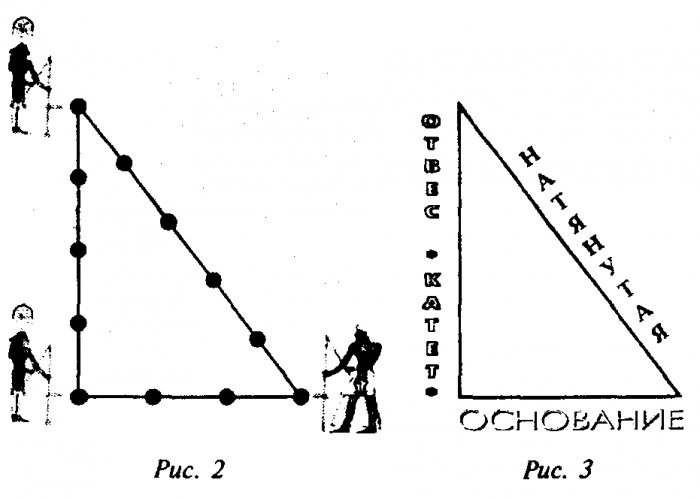
Египтяне 4000 лет назад для строительства пирамид использовали метод получения прямоугольного треугольника при помощи верёвки разделенной на 12 равных частей.

Понятие “египетский треугольник”.

Почему треугольник со сторонами 3, 4, 5 называют египетским?

А всё дело в том, что строителям Древнего Египта пирамид нужен был простой и надежный метод построения треугольника с прямым углом. И вот как они это реализовывали. Верёвку разбивали на двеадцать равновеликих частей, обозначив границы между соседними частями; концы верёвки соединяли. После этого 3 человека натягивали верёвку таким образом, чтобы она образовала треугольник, причем расстояния между каждыми двумя египтянами, тянущими веревку, составляли соответственно три части, четыре части и пять частей. Получался треугольник с прямым углом с катетами в три и четыре части и гипотенузой в пять частей. Известно, прямым был угол между сторонами в три и четыре части. Как известно, древнеегипетских землемеров, которые кроме обмеривания земельных наделов занимались построениями на местности, в древнем Египте их называли гарпедонаптами (что буквально переводится как «натягивающие верёвки»). Гарпедонапты занимали 3 место в иерархии жрецоы Древнего Египта.

Обратная теорема Пифагора.

Но из-за чего треугольник со сторонами 3, 4, 5 окажется прямоугольным? Большинство ответили бы на данный вопрос, что данный факт это теорема Пифагора: так как три в квадрате плюс четыре в квадрате равняется пяти в квадрате. Но теорема Пифагора говорит, что если треугольник с прямым углом, то тогда сумма квадратов 2-х его сторон равняется квадрату третьей. Здесь мы имеем дело с теоремой, обратной теореме Пифагора: если сумма квадратов 2-х сторон треугольника равна квадрату третьей, то тогда треугольник — прямоугольный.

Обрисованное практическое приложение обратной теоремы Пифагора относиться к далёкому прошлому. Едва ли кто-либо получает прямые углы таким методом сегодня. Но тем не менее данный способ является отличным математическим лайфхаком и может быть применён Вами в любой жизненной ситуации.

Метод определения прямоугольного треугольника при помощи верёвки из мира практики переместился в мир идей, подобно тому как многое из материальной культуры древности вошло в духовную культуру нынешней действительности.

Видео:Что такое египетский треугольник?Скачать

Глупая ошибка строителей – зачем строили «египетский треугольник»

Каких только правил не применяют начинающие строители, возводя дома или бани на своих участках. Но зачастую такие «потуги» сделать всё идеально приводят к противоположному результату. И дело даже не в том, что используемый способ не работает в принципе. Чаще домашние мастера сами до конца не понимают, для чего выполняется то или иное действие. В сегодняшней статье речь пойдёт об одном из способов разметки под фундамент, пришедшем из древних времён – «египетском треугольнике».

Видео:Что такое египетский треугольник ❓Скачать

Что такое «египетский треугольник», и откуда он появился

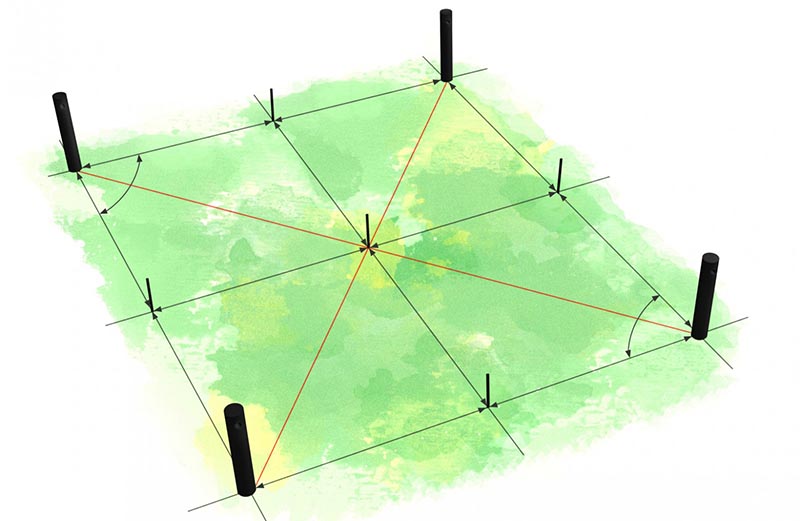
Придумали подобный способ замеров не древние египтяне, как могло бы показаться, судя по названию. На самом деле таким методом разметки пользовались строители ещё задолго до появления пирамид. Суть метода заключается в том, чтобы разделить квадрат будущего строения на два одинаковых треугольника со сторонами, относящимися друг к другу как 3:4:5.

Это должен быть прямоугольный треугольник, подчиняющийся теореме Пифагора. Наверняка все помнят её из школьной программы – сумма квадратов катета равна квадрату гипотенузы, и наоборот. Логически при совмещении этих треугольников должен получиться квадрат с идеально одинаковыми диагоналями. И вот тут начинается самое интересное.

Видео:Египетский треугольникСкачать

Глупая ошибка строителей

«Египетский треугольник» действительно может помочь в разметке периметра фундамента, однако применение этого метода требует сохранения чётких пропорций. Небольшое отклонение от них − и угол уже не будет прямым. А это приведёт к разнице длин стен. Не единичны случаи, когда при идеальном совпадении длин диагоналей стены получаются разными. Ведь если вдуматься, то трапеция также подходит под заданные параметры, её диагонали равны, в то время как верхняя и нижняя сторона имеют разные длины.

ФОТО: youc.ir Правильная трапеция также имеет одинаковые длины диагоналей, однако на квадрат она явно не тянет

Видео:8 класс, 16 урок, Теорема ПифагораСкачать

Как быть, если строение не подходит под размер 3×4

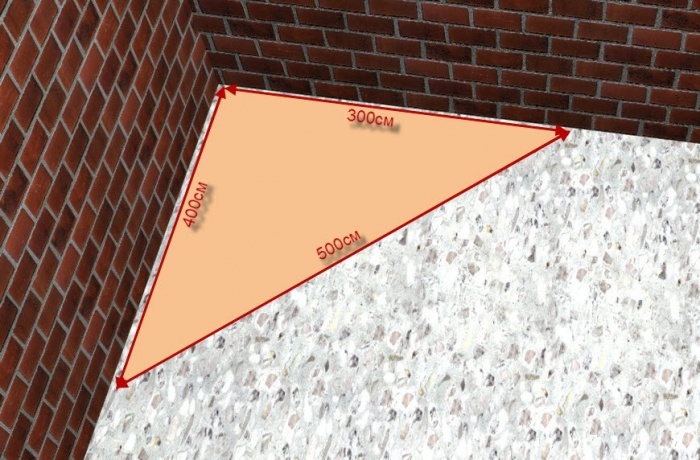
Понятно, что если стороны дома не подходят под заданный размер, придётся производить вычисления. Но здесь всё не так уж и сложно. К примеру, необходимо построить здание, размеры которого больше. Тогда можно сделать одну стену длиной 12 м, а вторую − 15 м. В этом случае, пользуясь всё той же теоремой Пифагора и особенностями «египетского треугольника», несложно вычислить необходимую длину диагонали (она же гипотенуза), которая будет равна 19,2 м.

ФОТО: fsks.ru Все углы разметки под фундамент должны быть идеально прямыми – это аксиома

«Египетский треугольник» − это способ разметки, используемый в строительстве с незапамятных времён. И то, что он и сейчас достаточно популярен, говорит о работоспособности метода. Главное – использовать его на полную, а не обходиться только поверхностными знаниями.

ФОТО: tvoidom-msk.ru Лучше потратить немного больше времени и вывести углы фундамента, чем впоследствии получить массу проблем при строительстве и отделке

Видео:Египетский треугольникСкачать

Другие размеры стен и применение к ним правила «египетского треугольника»

На самом деле, если разобраться с тем, как «работает» «египетский треугольник», можно вывести стены различной длины. Главное – это их соотношение друг с другом. Попробуем разобрать этот момент на примере.

Требуется, чтобы одна из стен была равна восьми метрам. Для того чтобы соотношение получилось верным, вторую стену нужно сделать длиной 6 м. В этом случае число 8 можно обозначить как 4 отрезка по 2 м, а 6 – как 3 отрезка по 2 м. Разобравшись с длиной стен, можно свободно вывести и длину диагонали, которая будет равна квадратному корню из 6×6+8×8 (квадратный корень из 100). Получается, диагональ должна быть равна 10 м. Всё крайне просто.

ФОТО: warfields.ru Можно использовать любые размеры, главное, чтобы они имели правильное соотношение

Видео:Решали пол-урока, а оказалось очень простоСкачать

Иные способы выведения прямого угла

Если нет желания заниматься выведением углов самостоятельно, а финансы позволяют обратиться за помощью к специалистам, можно вообще не думать об этом вопросе. Один звонок − и на участке уже находится геодезист с теоделитом, который в сжатые сроки сделает разметку. Однако в этом случае необходимо быть готовым к внушительным затратам на оплату его труда.

ФОТО: omegagalvanoplastia.com.br Теоделит – высокоточная техника, однако стоимость подобной разметки может влететь «в копеечку»

Если говорить о минимальных затратах, то, основываясь на прайс-листах фирм, оказывающих подобные услуги, вызов и работа геодезиста с инструментом обойдётся в 1 000 руб./час при минимальной оплате 7 000 руб. Дальше − больше. Разметка осей (2 точки) – ещё 3 000 рублей. Если же потребуется определить точные координаты по GPS, то здесь каждые три точки обойдутся владельцу в 5 000 руб. Можно посчитать, какова будет общая сумма (все цены указаны с учётом на конец сентября 2020 года). Не проще ли самому произвести все необходимые разметки? Ведь сэкономленные средства всегда можно потратить на что-то полезное в дальнейшем строительстве.

ФОТО: thelundreport.org Стоит приготовиться к тому, что карман значительно облегчится

Видео:КАК РЕШИТЬ ТРЕУГОЛЬНИК?Скачать

Заключительное слово

Что бы ни говорили противники описанного метода измерений, но «египетский треугольник» в значительной степени помогает строителям в выведении прямых углов. Конечно, при условии его правильного использования. Тем более что навязать 12 узлов на верёвке на определённом расстоянии один от другого много времени не потребует. Также это не потребует и финансовых затрат, связанных с наймом геодезиста с необходимым оборудованием.

ФОТО: profipol.dp.ua Так должны быть расположены узлы на верёвке для построения «египетского треугольника»

Очень надеемся, что сегодняшняя статья была полезна нашему уважаемому читателю и дала общее представление о «египетском треугольнике» и его применении. Если у вас по ходу ознакомления с предоставленной информацией возникли вопросы, редакция онлайн-журнала Homius будет рада на них ответить. Вам лишь нужно изложить суть в комментариях ниже. Там же можно обсудить, стоит ли пользоваться методами, проверенными временем, или давно пора о них забыть и перейти к более высокотехнологичным приспособлениям. Если статья понравилась, не забывайте ставить оценки. А мы напоследок предлагаем вашему вниманию короткий видеоролик, который поможет более полно раскрыть сегодняшнюю тему. Берегите себя, своих близких и будьте здоровы!

📸 Видео

Полуокружность в египетском треугольнике.Скачать

Делаем Египетский треугольник из верёвочки с узелками. Геометрия для детей. Математика - это красивоСкачать

Неравенства треугольника. 7 класс.Скачать

9 класс, 15 урок, Решение треугольниковСкачать

Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Египетский треугольникСкачать

Как решать задания в ОГЭ с помощью египетского треугольника? Лайфхак по математике 🧮📚Скачать

Теорема Пифагора. 8 КЛАСС | Математика | TutorOnlineСкачать

Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать