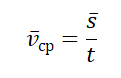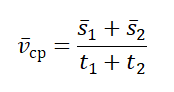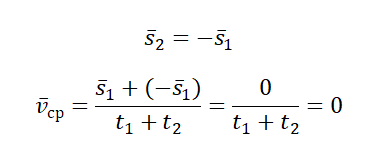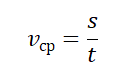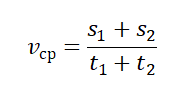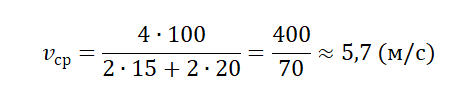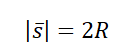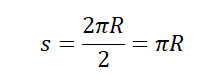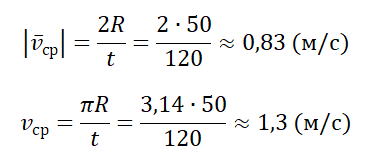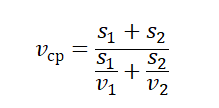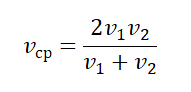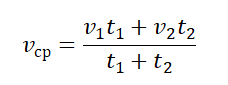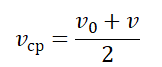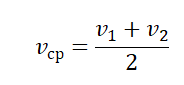О чем эта статья:
- Прямолинейное равномерное движение
- Скалярные величины (определяются только значением)
- Векторные величины (определяются значением и направлением)
- Проецирование векторов
- Уравнение движения
- Прямолинейное равноускоренное движение
- Уравнение движения и формула конечной скорости
- Движение по вертикали
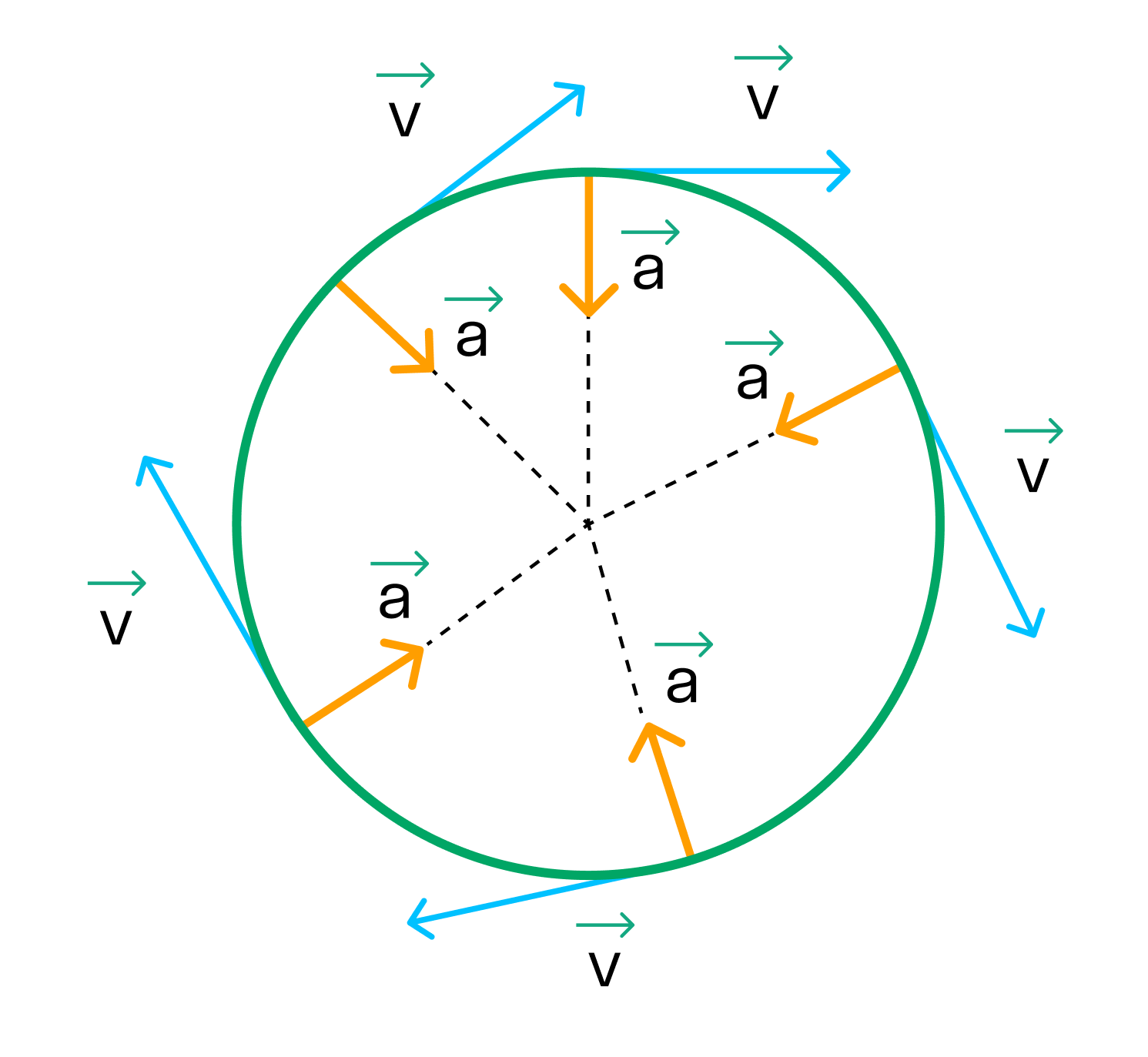
- Движение по окружности
- Центростремительное ускорение
- Неравномерное движение и средняя скорость
- теория по физике 🧲 кинематика
- Средняя векторная скорость
- Средняя скалярная скорость
- Скорость — это вектор или скаляр?
- Начальная скорость V?
- Что такое физика скоростей в 10 классе?
- Электрическое поле — это скаляр?
- Ток — это тензорная величина?
- Подходит ли текущий скаляр или вектор?
- Что такое формула единичного вектора?
- Какие бывают 3 типа векторов?
- Что такое векторная формула?
- Какая величина есть сила?
- Текущая скалярная величина?
- Что такое сила, скалярная или векторная?
- Что такое начальная скорость?
- Что такое скорость в уроке физики 9?
- Что такое скорость с примером?
- Какая формула начальной скорости?
- Может ли начальная скорость быть нулевой?
- Может ли начальная скорость быть отрицательной?
- 🔍 Видео
Видео:Физика | Ликбез по векторамСкачать

Прямолинейное равномерное движение
Движение по прямой, при котором тело проходит равные участки пути за равные промежутки времени называют прямолинейным равномерным. Это любое движение с постоянной скоростью.
Например, если у вас ограничение скорости на дороге 60 км/ч и у вас нет никаких препятствий на пути, то вы скорее всего будете двигаться прямолинейно равномерно.
Мы можем охарактеризовать это движение следующими величинами.
Скалярные величины (определяются только значением)
- Время — в международной системе единиц СИ измеряется в секундах [с].
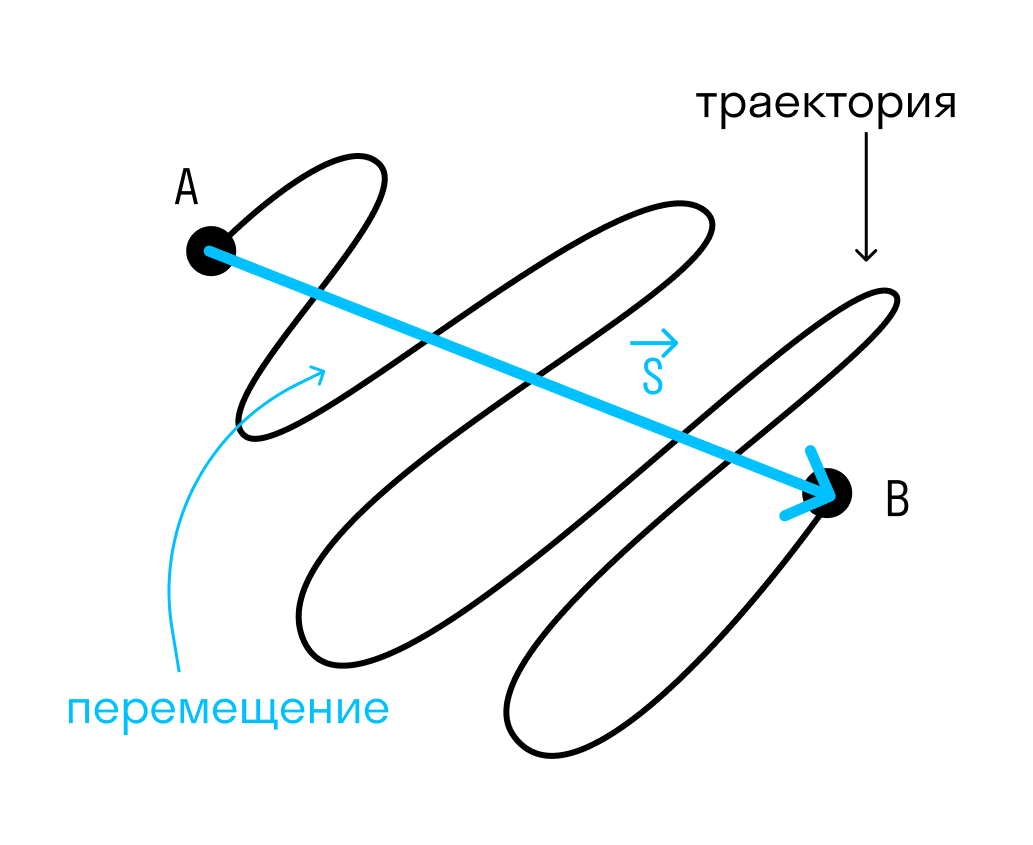
- Путь — длина траектории (линии, по которой движется тело). В случае прямолинейного равномерного движения — длина отрезка [м].
Векторные величины (определяются значением и направлением)
- Скорость — характеризует быстроту перемещения и направление движения материальной точки [м/с].
- Перемещение — вектор, проведенный из начальной точки пути в конечную [м].
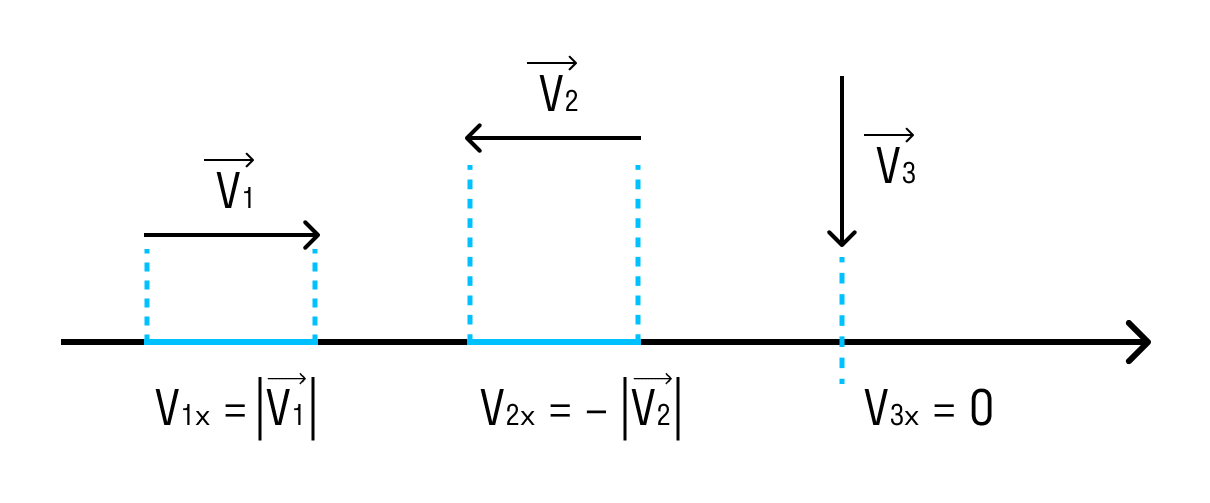
Проецирование векторов
Векторное описание движения полезно, так как на одном чертеже всегда можно изобразить много разнообразных векторов и получить перед глазами наглядную «картину» движения.
Однако всякий раз использовать линейку и транспортир, чтобы производить действия с векторами, очень трудоёмко. Поэтому эти действия сводят к действиям с положительными и отрицательными числами — проекциями векторов.
Если вектор сонаправлен с осью, то его проекция равна длине вектора. А если вектор противоположно направлен оси — проекция численно равна длине вектора, но отрицательна. Если вектор перпендикулярен — его проекция равна нулю.
Скорость может определяться по перемещению и пути, только это будут две разные характеристики. Скорость — это векторная физическая величина, характеризующая быстроту перемещения, а средняя путевая скорость — это отношение длины пути ко времени, за которое путь был пройден.
Скорость
— скорость [м/с]
— перемещение [м]
— время [с]
Средняя путевая скорость
V ср.путевая = S/t
V ср.путевая — средняя путевая скорость [м/с]
В чем разница между перемещением и путем?
Перемещение — это вектор, проведенный из начальной точки в конечную, а путь — это длина траектории.
Задача
Найдите, с какой средней путевой скоростью должен двигаться автомобиль, если расстояние от Санкт-Петербурга до Великого Новгорода в 210 километров ему нужно пройти за 2,5 часа. Ответ дайте в км/ч.
Решение:
Возьмем формулу средней путевой скорости
V ср.путевая = S/t
V ср.путевая = 210/2,5 = 84 км/ч
Ответ: автомобиль будет двигаться со средней путевой скоростью равной 84 км/ч
Уравнение движения
Одна из основных задач механики — определение положения тела относительно других тел в данный момент времени. Для решения этой задачи помогает уравнение движения, то есть зависимость координаты тела от времени х = х(t).
Уравнение движения
x(t) — искомая координата в момент времени t [м]
x0 — начальная координата [м]
vx — скорость тела в данный момент времени [м/с]
t — момент времени [с]
Если положительное направление оси ОХ противоположно направлению движения тела, то проекция скорости тела на ось ОХ отрицательна, скорость меньше нуля (v
Задачка
Мотоцикл движется по закруглённому участку дороги радиусом 120 м со скоростью 36 км/ч. Чему равно центростремительное ускорение мотоцикла?
Решение:
Возьмем формулу центростремительного ускорения тела
В условии задачи скорость дана в километрах в час, а радиус в метрах. Значит, нужно перевести скорость в м/с, чтобы избежать коллапса в решении.
Теперь можно подставить значения в формулу:
aц = 10 2 /120 = 100/120 = 10/12 ≃ 0,83 м/с 2
Ответ: центростремительное ускорение мотоциклиста равно 0,83 м/с 2
Эту и другие темы мы разбираем на курсе физики за 9 класс.
Видео:Урок 8. Векторные величины. Действия над векторами.Скачать

Неравномерное движение и средняя скорость
теория по физике 🧲 кинематика
Неравномерное движение — движение с переменной скоростью, которая может менять как направление, так и модуль.
Неравномерное движение можно охарактеризовать средней скоростью. Различают среднюю векторную и среднюю скалярную скорости.
Видео:2.1. Скалярные и векторные физические величиныСкачать

Средняя векторная скорость
Средняя векторная скорость — это скорость, равная отношению перемещения тела ко времени, в течение которого это перемещение было совершено.
v ср — средняя векторная скорость, s — перемещение тела, совершенное за время t
Направление вектора средней скорости всегда совпадает с направлением вектора перемещения.
Чтобы вычислить среднюю векторную скорость, нужно поделить сумму всех перемещений на сумму всех временных промежутков, в течение которых эти перемещения были совершены:
Пример №1. Миша пробежал стометровку за 16 секунд. Через 1 минуту он вернулся на старт. Найти среднюю векторную скорость мальчика.
Миша совершил одинаковые по модулю, но разные по направлению перемещения. При сложении этих векторов получается 0. Поэтому средняя векторная скорость также равна нулю:
Видео:Физика 7 класс (Урок№8 - Скорость.)Скачать

Видео:Физика: Понятие Вектор, Вектор СкоростиСкачать

Средняя скалярная скорость
Средняя скалярная (путевая) скорость — это скорость, равная отношению пути, пройденного телом, ко времени, в течение которого этот путь был пройден.
vср — средняя путевая скорость, s — путь, пройденный телом за время t
Чтобы вычислить среднюю путевую скорость, нужно поделить сумму всех путей на сумму всех временных промежутков, в течение которых эти пути были преодолены:
Пример №2. Мальчик пробежал по периметру квадратного поля сто стороной 100 м. На первые две стороны мальчик потратил по 15 секунд, а на последние две — по 20 секунд. Найти среднюю путевую скорость мальчика.
У квадрата 4 стороны, поэтому путь мальчика составляют 4 дистанции по 100 м каждая. Поэтому средняя путевая скорость равна:
Средняя скалярная скорость всегда больше или равна модулю средней векторной скорости:
- vср= v ср, если путь равен модулю перемещения. Так бывает в случае равномерного прямолинейного движения.
- vср>v ср, если путь больше модуля перемещения. Так бывает в случае неравномерного прямолинейного или любого криволинейного движения.
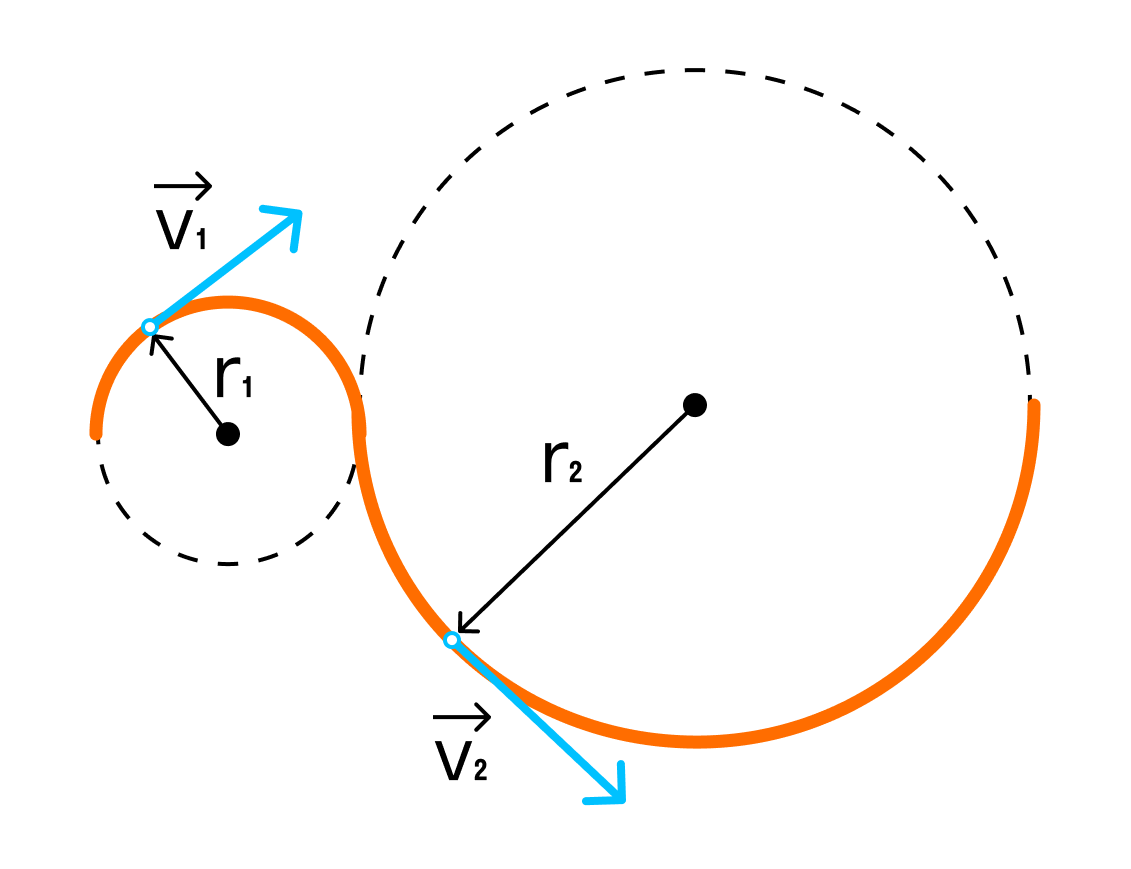
Пример №3. Рыболов остановился на берегу круглого пруда и увидел на противоположном берегу удобное для рыбалки место. Он к нему шел в течение 2 минут. Вычислите среднюю путевую и среднюю векторную скорости рыболова после того, как он придет на новое место, если радиус пруда равен 50 м.
Две противоположные точки окружности соединяются отрезком, проходящим через его центр — диаметром. Поэтому модуль вектора перемещения равен двум радиусам пруда:
Чтобы дойти до диаметрально противоположной точки окружности, нужно пройти путь, равный половине окружности:
Переведя 2 минуты в СИ, получим 120 с. Модуль средней векторно скорости равен:
Видео:Мгновенная скорость (видео 6)| Векторы. Прямолинейное движение | ФизикаСкачать

- Если известны скорости на первой и второй половине пути (s1=s2), средняя скорость равна:
- Если известно время прохождения отдельных участков пути и скорости движения на этих участках, средняя скорость равна:
- Если тело движется прямолинейно и равноускорено, его средняя скорость равна половине суммы начальной и конечной скорости:
- Если известны скорости тела за равные промежутки времени, его средняя скорость равна:
Пример №4. Первые полчаса автомобиль двигался со скоростью 90 км/ч, а потом 1 час он двигался со скоростью 60 км/ч. Найти среднюю скорость автомобиля.
Нам известны скорости на каждом из участков пути и время, в течение которого каждый из этих участков был преодолен. Поэтому:
Видео:Зачем нужен ВЕКТОР. Объяснение смыслаСкачать

Скорость — это вектор или скаляр?
by Знаменитости Updates 3.4k Просмотры
Скорость — это скалярная величина — это скорость изменения расстояния, пройденного объектом, в то время как скорость это векторная величина — это скорость объекта в определенном направлении.
Таким образом, что такое скорость и ее типы?
Физический термин, скорость описывает движение объектов. Скорость измеряет движение объектов в зависимости от их скорости и направления.. Скорость объекта измеряет расстояние, которое он преодолевает за определенный период времени. … Скорость — это векторная величина, поскольку она описывает как скорость, так и направление.
Имея это в виду, почему Current является скаляром?
Электрический ток — это скалярная величина. … В случае электрического тока, когда два тока встречаются в соединении, их результирующий ток будет алгебраической суммой, а не векторной суммой. Следовательно, электрический ток — это скалярная величина, хотя он обладает величиной и направленностью.
Кроме того, что такое вектор, приведите пример?
Например, смещение, скорость и ускорение — векторные величины, а скорость (величина скорости), время и масса — скаляры. Чтобы считаться вектором, величина, имеющая величину и направление, также должна подчиняться определенным правилам комбинирования.
Является ли сила скалярной величиной?
Скалярные величины определяется величиной без применимого направления. … Некоторые общие скалярные величины — это расстояние, скорость, масса и время. Некоторые общие векторные величины — это сила, скорость, смещение и ускорение.
Во-вторых, какие 3 типа скорости?
Различные типы скоростей равномерная скорость, переменная скорость, средняя скорость и мгновенная скорость.
Начальная скорость V?
Конечная скорость (v) объекта равна начальной скорости (u) этого объекта плюс ускорение (a) объекта, умноженное на прошедшее время (t) от u до v.
Что такое физика скоростей в 10 классе?
Хотя скорость и скорость часто используются как синонимы, в физике это разные понятия. Скорость (v) — это векторная величина, которая измеряет смещение (или изменение положения, Δs) за изменение во времени (Δt), представленное уравнением v = Δs / Δt.
Электрическое поле — это скаляр?
Нет, электрическое поле не является скаляром. Электричество — это векторная величина. Мы знаем, что электрическое поле — это отношение силы к единице испытательного заряда. Поскольку сила является векторной величиной, электрическое поле также является векторной величиной.
Ток — это тензорная величина?
И скаляры, и векторы являются частными случаями тензоров. Ток — это скаляр. Плотность тока — это вектор. Поскольку скаляры и векторы являются тензорами, это означает, что ток и плотность тока являются тензорами.
Подходит ли текущий скаляр или вектор?
Примечание: ток вектор потому что у него есть величина и направление. Но дело в том, что вектор всегда подчиняется закону сложения векторов. Поскольку ток ему не подчиняется и следует алгебраическому сложению, токи скалярны.
Что такое формула единичного вектора?
Ортопедические векторы вектора направлены по осям. Единичные векторы в трехмерном пространстве можно представить следующим образом: v = х ^ + у ^ + г ^. В трехмерной плоскости вектор v будет обозначаться тремя перпендикулярными осями (осью x, y и z). В математических обозначениях единичный вектор по оси x представлен буквой i ^.
Какие бывают 3 типа векторов?
Типы списков векторов
- Нулевой вектор.
- Единичный вектор.
- Вектор положения.
- Со-начальный вектор.
- Как и в отличие от векторов.
- Копланарный вектор.
- Коллинеарный вектор.
- Равный вектор.
Что такое векторная формула?
Векторное уравнение прямой, проходящей через точку a в направлении d: г = а + тд , где t меняется.
Какая величина есть сила?
Сила векторная величина. Как было сказано ранее, векторная величина — это величина, которая имеет как величину, так и направление. Чтобы полностью описать силу, действующую на объект, вы должны описать как величину (размер или числовое значение), так и направление.
Текущая скалярная величина?
Электрический ток — это скалярная величина. Любая физическая величина определяется как векторная величина, если величина имеет как величину, так и направление, но есть некоторые другие факторы, которые показывают, что электрический ток является скалярной величиной. Когда два тока встречаются в точке, результирующий ток будет алгебраической суммой.
Что такое сила, скалярная или векторная?
Сила вектор и, следовательно, он имеет как направление, так и величину. Единица силы в системе СИ — Ньютон (Н). Один ньютон равен 1 кг × м / с2. Другое определение силы; Сила пропорциональна ускорению, которое определяется как скорость изменения скорости.
Что такое начальная скорость?
Следовательно, начальная скорость равна скорость объекта до эффекта ускорения, что вызывает изменение. После ускорения объекта в течение некоторого времени скорость будет конечной скоростью.
Что такое скорость в уроке физики 9?
Вход в музей Мадам Тюссо Расстояние, пройденное телом за единицу времени. Это расстояние, которое проходит тело за единицу времени в заданном направлении. У него есть только Величина.
Что такое скорость с примером?
Скорость — это скорость с направлением. Сказать, что Собака Ариэль бежит со скоростью 9 км / ч (километров в час), — это скорость. Но сказать, что он бежит на запад со скоростью 9 км / ч, — это скорость. Скорость. Скорость.
Какая формула начальной скорости?
Очевидно, эта скорость на временном интервале t = 0. Она обозначается буквой u. Ниже приведены три формулы начальной скорости, основанные на уравнениях движения, если время, ускорение и скорость известны.
.
Формулы для начальной скорости.
| u | Начальная скорость |
|---|---|
| t | затраченное время |
| s | смещение |
| a | ускорение |
Может ли начальная скорость быть нулевой?
Когда тело выходит из состояния покоя или меняет направление движения, это называется начальной скоростью. Мы обычно считаем начальная скорость равна нулю(u = 0), только когда объект стартует из состояния покоя. Обычно в момент времени (t = 0) начальная скорость равна нулю.
Может ли начальная скорость быть отрицательной?
Скорость может быть указана в любой конкретный момент времени. … Поскольку конечное положение объекта (rfinal) может быть положительным, отрицательным или нулевым, а также больше, меньше или совпадает с исходным положением (rinitial), скорость может быть положительной, отрицательной или нулевой.
Последнее обновление: 19 дней назад — Авторов: 19 — Авторов: 23 — Ссылки: 26 интервью и постов; 6 Видео.
Узнайте все о своем любимом. знаменитости в Интервью со знаменитостями и не забудьте поделиться этим постом!
🔍 Видео
2.4. Радиус-вектор и вектор перемещенияСкачать

СКАЛЯРНОЕ УМНОЖЕНИЕ ВЕКТОРОВ ЧАСТЬ I #математика #егэ #огэ #формулы #профильныйегэ #векторыСкачать

Физика.7 класс. Скалярные и векторные физические величины /11.09.2020/Скачать

Урок 3 (осн). Физические величины и единицы их измеренияСкачать

УСКОРЕНИЕ - Что такое равноускоренное движение? Как найти ускорение // Урок Физики 9 классСкачать

18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Физика 13. Формула расчёта скорости. Определение вектора скорости — Академия занимательных наукСкачать

Мгновенная скорость (видео 6) | Векторы. Прямолинейное движение | ФизикаСкачать

Вектор скорости и траекторияСкачать

Векторы и действия над ними, проекция вектора на координатные оси. 9 класс.Скачать