- Треугольник произвольный
- Свойства
- Признаки равенства треугольников
- Биссектриса, высота, медиана
- Средняя линия треугольника
- Вписанная окружность
- Описанная окружность
- Соотношение сторон в произвольном треугольнике
- Площадь треугольника
- math4school.ru
- Треугольники
- Основные свойства
- Равенство треугольников
- Подобие треугольников
- Медианы треугольника
- Биссектрисы треугольника
- Высоты треугольника
- Серединные перпендикуляры
- Окружность, вписанная в треугольник
- Окружность, описанная около треугольника
- Расположение центра описанной окружности
- Равнобедренный треугольник
- Равносторонний треугольник
- Прямоугольный треугольник
- Вневписанные окружности
- Теоремы синусов, косинусов, тангенсов; формулы Мольвейде
- Треугольник. Формулы и свойства треугольников.
- Типы треугольников
- По величине углов
- По числу равных сторон
- Вершины углы и стороны треугольника
- Свойства углов и сторон треугольника
- Теорема синусов
- Теорема косинусов
- Теорема о проекциях
- Формулы для вычисления длин сторон треугольника
- Медианы треугольника
- Свойства медиан треугольника:
- Формулы медиан треугольника
- Биссектрисы треугольника
- Свойства биссектрис треугольника:
- Формулы биссектрис треугольника
- Высоты треугольника
- Свойства высот треугольника
- Формулы высот треугольника
- Окружность вписанная в треугольник
- Свойства окружности вписанной в треугольник
- Формулы радиуса окружности вписанной в треугольник
- Окружность описанная вокруг треугольника
- Свойства окружности описанной вокруг треугольника
- Формулы радиуса окружности описанной вокруг треугольника
- Связь между вписанной и описанной окружностями треугольника
- Средняя линия треугольника
- Свойства средней линии треугольника
- Периметр треугольника
- Формулы площади треугольника
- Формула Герона
- Равенство треугольников
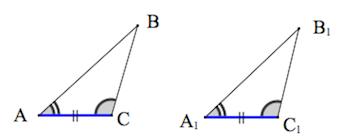
- Признаки равенства треугольников
- Первый признак равенства треугольников — по двум сторонам и углу между ними
- Второй признак равенства треугольников — по стороне и двум прилежащим углам
- Третий признак равенства треугольников — по трем сторонам
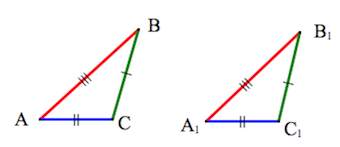
- Подобие треугольников
- Признаки подобия треугольников
- Первый признак подобия треугольников
- Второй признак подобия треугольников
- Третий признак подобия треугольников
Треугольник произвольный
Треугольник – это многоугольник с тремя сторонами (тремя углами).
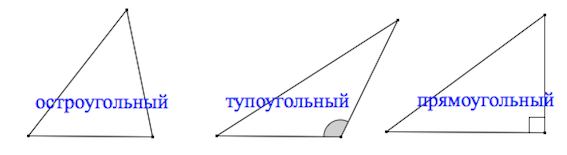
Виды треугольников :+ показать
Остроугольный треугольник – треугольник, у которого все углы острые (то есть меньше 90˚).
Тупоугольный треугольник – треугольник, у которого один из углов тупой (больше 90˚).
Прямоугольный треугольник – треугольник, у которого один из углов прямой (равен 90˚).
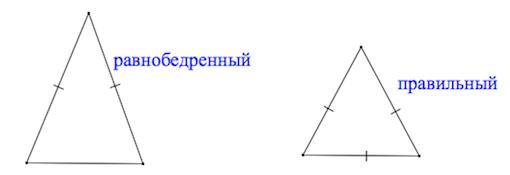
Равнобедренным называется треугольник, у которого две стороны равны. Эти стороны называются боковыми , третья сторона называется основанием .
Равносторонний (правильный) треугольник – треугольник, у которого все три стороны равны.
Свойства
1. Против большей стороны лежит больший угол, и наоборот.
2. Против равных сторон лежат равные углы, и наоборот.
3. Сумма углов треугольника равна 180 º .
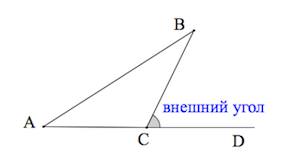
4. Внешний угол треугольника равен сумме внутренних углов,
не смежных с ним:
(Внешний угол образуется в результате продолжения одной из сторон треугольника).
5. Любая сторона треугольника меньше суммы двух других сторон.
Признаки равенства треугольников
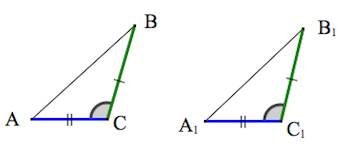
1. Треугольники равны, если у них соответственно равны две стороны и угол между ними.
2 . Треугольники равны, если у них соответственно равны два угла и прилегающая к ним сторона.
3. Треугольники равны, если у них соответственно равны три стороны.
Биссектриса, высота, медиана
Здесь подробно о биссектрисе, высоте, медиане треугольника.
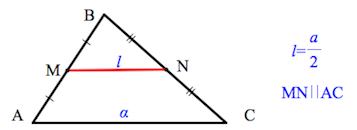
Средняя линия треугольника
Средняя линия треугольника – отрезок, соединяющий середины двух сторон треугольника.
Средняя линия треугольника параллельна третьей стороне и равна ее половине.
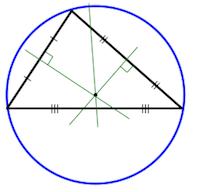
Вписанная окружность
Центр вписанной окружности – точка пересечения биссектрис треугольника.
Описанная окружность
Центр описанной окружности – точка пересечения серединных перпендикуляров.
Соотношение сторон в произвольном треугольнике
Теорема косинусов:
Теорема синусов:
Площадь треугольника
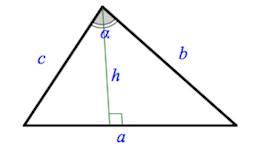
Через две стороны и угол между ними
Через радиус описанной окружности
Через радиус вписанной окружности
, где
– полупериметр
, где
– полупериметр
Смотрите также площадь треугольника здесь.
Чтобы не потерять страничку, вы можете сохранить ее у себя:
Есть пара ошибок в формулах. В частности в формуле вычисления площади через 2 стороны и угол между ними, в теореме Синусов, в разделе “свойства”.
А вообще отличные статьи, очень выручают, всё понятно и доступно, премного благодарен 😉
Анатолий, спасибо!
В разделе “свойства” ошибок не нашла…
В теореме синусов, – да… не пропечаталась буква гамма. Подправила.
В формуле площади треугольника, вы правы – картинка не соответствовала формуле. Исправила.
К сожалению, ошибки сразу не всегда замечаются.
Благодарю еще раз!
В разделе свойства:
Да, не хватало значка «» у А. Спасибо! 😉
Здраствуйте! Мне нужна ваша помощь!
Задача: ВЕРШИНЫ ТРЕУГОЛЬНИКА ДЕЛЯТ ОПИСАННУЮ ОКОЛО НЕГО ОКРУЖНОСТЬ НА ТРИ ДУГИ, ДЛИНЫ КОТОРЫХ ОТНОСЯТСЯ КАК 6:7:33. НАЙДИТЕ РАДИУС ОКРУЖНОСТИ, ЕСЛИ МЕНЬШАЯ ИЗ СТОРОН РАВНА 11.
Подозреваю, у вас опечатка в условии…
Если длины дуг (а значит и их градусные меры) находятся в отношении , то выходим на уравнение
Откуда
Значит угол треугольника, что напротив меньшей стороны, есть
Применяем теорему синусов: , откуда
спасибо я так и думал а то не могу решить и всё
СПАСИБО!
Здравствуйте. Пожалуйста, объясните, как решить задачу:
Вписанная в теругольник ABC окружность касается сторон AB, BC и AC в точках K,L и М соответственно.Найдите KL, если AM=2, МС=3 и угол С=π/3
Очевидно,
Примите за
.
Примените к треугольнику теорему косинусов:
Найдете , далее можно найти угол
и из треугольника
найти
Спасибо большое за ваш сайт. Очень радует, тот факт, что когда люди не понимают какую-нибудь задачу, вы помогаете решить. Спасибо. Побольше бы таких сайтов, всё понятно и доступно
Видео:Геометрия. 7 класс. Теоремы. Т5. Первое свойство равнобедренного треугольника.Скачать

math4school.ru
Видео:Треугольники. 7 класс.Скачать

Треугольники
Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Основные свойства

Треугольник – это геометрическая фигура, которая состоит из трёх точек, не лежащих на одной прямой (вершин треугольника) и трёх отрезков с концами в этих точках (сторон треугольника).
Углами (внутренними углами) треугольника называются три угла, каждый из которых образован тремя лучами, выходящими из вершин треугольника и проходящими через две другие вершины.
Внешним углом треугольника называется угол, смежный внутреннему углы треугольника.
Сумма углов треугольника равна 180°:
Внешний угол равен сумме двух внутренних углов, не смежных с ним, и больше любого внутреннего, с ним не смежного:
Длина каждой стороны треугольника больше разности и меньше суммы длин двух других сторон:
В треугольнике против большего угла лежит большая сторона, против большей стороны лежит больший угол:

Средней линией треугольника называется отрезок, который соединяет середины двух его сторон.
Средняя линия треугольника параллельна одной из его сторон и равна её половине:
Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Равенство треугольников

Треугольники называются равными, если у них соответствующие стороны равны и соответствующие углы равны:
У равных треугольников все соответствующие элементы равны (стороны, углы, высоты, медианы, биссектрисы, средние линии и т.д.)
В равных треугольниках против равных сторон лежат равные углы, а против равных углов – равные стороны.

Первый признак равенства треугольников.
Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны:

Второй признак равенства треугольников.
Если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны:

Третий признак равенства треугольников.
Если три стороны одного треугольника равны соответственно трём сторонам другого треугольника, то такие треугольники равны:
Видео:Как ПОНЯТЬ ГЕОМЕТРИЮ за 5 минут — Подобие ТреугольниковСкачать

Подобие треугольников

Подобными называются треугольники, у которых соответствующие стороны пропорциональны.
Коэффициент пропорциональности называется коэффициентом подобия:
Два треугольника подобны, если:
- Два угла одного треугольника равны двум углам другого треугольника.
- Две стороны одного треугольника пропорциональны двум сторонам другого, и углы, образованные этими сторонами, равны.
- Стороны одного треугольника пропорциональны сторонам другого.
У подобных треугольников соответствующие углы равны, а соответствующие отрезки пропорциональны:
Отношение периметров подобных треугольников равно коэффициенту подобия.
Отношение площадей подобных треугольников равно квадрату коэффициента подобия.

Прямая, пересекающая две стороны треугольника, и параллельная третьей, отсекает треугольник, подобный данному:

Три средние линии треугольника делят его на четыре равных треугольника, подобные данному, с коэффициентом подобия ½:
Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Медианы треугольника

Медианой треугольника называется отрезок, который соединяет вершину треугольника с серединой противолежащей стороны.
Три медианы треугольника пересекаются в одной точке, делящей медианы в отношении 2:1, считая от вершины:
- Медиана делит треугольник на два равновеликих (с равными площадями) треугольника.
- Три медианы треугольника делят его на шесть равновеликих треугольников:

Длины медиан, проведённых к соответствующим сторонам треугольника, равны:
Видео:Геометрия 7 класс (Урок№15 - Решение задач на признаки равенства треугольников.)Скачать

Биссектрисы треугольника

Биссектрисой треугольника, проведённой из данной вершины, называется отрезок биссектрисы угла треугольника, соединяющий эту вершину с точкой на противолежащей стороне.
Биссектрисы внутренних углов треугольника пересекаются в одной точке, находящейся внутри треугольника, равноудалённой от трёх его сторон, которая является центром окружности, вписанной в данный треугольник.
Биссектриса внутреннего угла треугольника делит противолежащую углу сторону на отрезки, пропорциональные двум другим сторонам:
Длина биссектрисы угла А :

Биссектрисы внутреннего и смежного с ним внешнего угла перпендикулярны.
Биссектриса внешнего угла треугольника делит (внешне) противолежащую сторону на отрезки, пропорциональные двум другим сторонам.
BL – биссектриса угла В ;
ВЕ – биссектриса внешнего угла СВК :
Видео:ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

Высоты треугольника

Высотой треугольника называется перпендикуляр, опущенный из любой вершины треугольника на противолежащую сторону или на продолжение стороны.
Высоты треугольника пересекаются в одной точке, которая называется ортоцентром треугольника.
Высоты треугольника обратно пропорциональны его сторонам:
Длина высоты, проведённой к стороне а :
Видео:Построение медианы в треугольникеСкачать

Серединные перпендикуляры

Серединный перпендикуляр – это прямая, которая проходит через середину стороны треугольника перпендикулярно к ней.
Три серединных перпендикуляра треугольника пересекаются в одной точке, которая является центром окружности, описанной около данного треугольника.
Точка пересечения биссектрисы угла треугольника с серединным перпендикуляром противолежащей стороны лежит на окружности, описанной около данного треугольника.
Видео:Вся геометрия за 45 минут | Геометрия 7-9 классыСкачать

Окружность, вписанная в треугольник

Окружность называется вписанной в треугольник, если она касается всех его сторон.
Точки касания вписанной окружности сторон треугольника отсекают от его сторон три пары равных между собой отрезков:
Радиус вписанной в треугольник окружности – расстояние от её центра до сторон треугольника:
Видео:Почему углы при основании равны в равнобедренном треугольникеСкачать
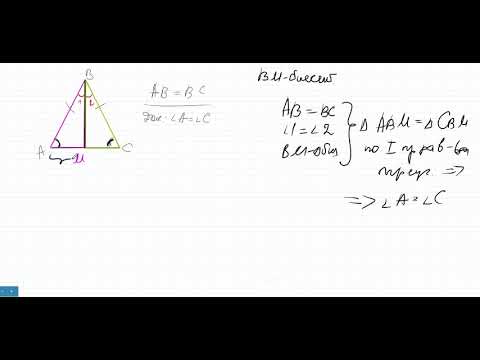
Окружность, описанная около треугольника

Окружность называется описанной около треугольника, если она проходит через все его вершины.
Радиус описанной окружности:
Видео:Строим треугольник по трем сторонам (Задача 5).Скачать

Расположение центра описанной окружности



Видео:SOS-ГЕОМЕТРИЯ! Отрезки и углы, смежные и вертикальные углы | Математика TutorOnlineСкачать

Равнобедренный треугольник

Треугольник называется равнобедренным, если у него две стороны равны. Равные стороны называют боковыми сторонами, а третью – основанием равнобедренного треугольника.
В равнобедренном треугольнике углы при основании равны: ∠ A = ∠ C.
В равнобедренном треугольнике медиана, проведённая к основанию, является и биссектрисой, и высотой: BL – медиана, биссектриса, высота.

Основные формулы для равнобедренного треугольника:
Видео:ГЕОМЕТРИЯ 7 класс : Решение задач по теме "Равнобедренный треугольник"Скачать

Равносторонний треугольник

Треугольник у которого все стороны равны называется равносторонним или правильным треугольником.
Центры вписанной и описанной окружностей правильного треугольника совпадают.
Все углы равностороннего треугольника равны:

Каждая медиана равностороннего треугольника совпадает с биссектрисой и высотой, которые проведены из той же вершины:
Основные соотношения для элементов равностороннего треугольника
Видео:Геометрия 9 класс (Урок№30 - Поворот.)Скачать

Прямоугольный треугольник

Треугольник называется прямоугольным, если у него есть прямой угол.
Стороны, прилежащие к прямому углу, называются катетами, противолежащая прямому углу – гипотенузой.
Прямоугольные треугольники равны если у них равны:
- два катета;
- катет и гипотенуза;
- катет и прилежащий острый угол;
- катет и противолежащий острый угол;
- гипотенуза и острый угол.
- одному острому углу;
- из пропорциональности двух катетов;
- из пропорциональности катета и гипотенузы.

Катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу:
Высота прямоугольного треугольника, проведённая из вершины прямого угла, есть среднее пропорциональное между проекциями катетов на гипотенузу:
Высота прямоугольного треугольника, проведённая из вершины прямого угла, может быть определена через катеты и их проекции на гипотенузу:
Медиана, проведённая из вершины прямого угла, равна половине гипотенузы:
Высота прямоугольного треугольника, проведённая из вершины прямого угла, делит данный треугольник на два треугольника, подобные данному:
Площадь прямоугольного треугольника можно определить
через катеты:
через катет и острый угол:
через гипотенузу и острый угол:

Центр описанной окружности совпадает с серединой гипотенузы.
Радиус описанной окружности:

Радиус вписанной окружности:
Видео:Равнобедренный треугольникСкачать

Вневписанные окружности

Три окружности, каждая из которых касается одной стороны (снаружи) и продолжений двух других сторон треугольника, называются вневписанными.
Центр вневписанной окружности лежит не пересечении биссектрисы одного внутреннего угла и биссектрис внешних углов при двух других вершинах.
Так точка О1 , центр одной из вневписанных окружностей Δ ABC , лежит на пересечении биссектрисы ∠ A треугольника ABC и биссектрис BО1 и C О1 внешних углов Δ ABC при вершинах B и C .
Таким образом, шесть биссектрис треугольника – три внутренние и три внешние – пересекаются по три в четырёх точках – центрах вписанной и трёх вневписанных окружностей.
Δ ABC является ортоцентричным в Δ О1О2О3 (точки A , B и C – основания высот в Δ О1О2О3 ).
В Δ ABC углы равны 180°–2 О1 , 180°–2 О2 , 180°–2 О3 .
Радиус окружности, описанной около Δ О1О2О3 , равен 2 R , где R – радиус окружности, описанной около Δ ABC .
Δ ABC имеет наименьший периметр среди всех треугольников, вписанных в Δ О1О2О3 .
Если ra , rb , rс – радиусы вневписанных окружностей в Δ ABC , то в Δ ABC верно:
для r –
для R –
для S –
для самих ra , rb , rс –
Видео:Многоугольники. 5 класс.Скачать

Теоремы синусов, косинусов, тангенсов; формулы Мольвейде

Теорема косинусов. Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними:
- если c 2 > a 2 +b 2 , то угол γ – тупой ( cos γ
- если c 2 2 +b 2 , то угол γ – острый ( cos γ > 0 );
- если c 2 = a 2 +b 2 , то угол γ – прямой ( cos γ = 0 ).
Теорема синусов. Стороны треугольника пропорциональны синусам противолежащих углов. Коэффициент пропорциональности равен диаметру описанной окружности:
Теорема тангенсов (формула Региомонтана):
Видео:Определение натуральной величины треугольника АВС методом замены плоскостей проекцииСкачать

Треугольник. Формулы и свойства треугольников.
Видео:5 Загадочных Мест, Не Менее Таинственных, чем Бермудский ТреугольникСкачать

Типы треугольников
По величине углов
По числу равных сторон
Видео:КАК РЕШАТЬ ЗАДАЧИ ПО ГЕОМЕТРИИ? | МатематикаСкачать

Вершины углы и стороны треугольника
Свойства углов и сторон треугольника
Сумма углов треугольника равна 180°:
В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы:
если α > β , тогда a > b
если α = β , тогда a = b
Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:
a + b > c
b + c > a
c + a > b
Теорема синусов
Стороны треугольника пропорциональны синусам противолежащих углов.
| a | = | b | = | c | = 2R |
| sin α | sin β | sin γ |
Теорема косинусов
Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.
a 2 = b 2 + c 2 — 2 bc · cos α
b 2 = a 2 + c 2 — 2 ac · cos β
c 2 = a 2 + b 2 — 2 ab · cos γ
Теорема о проекциях
Для остроугольного треугольника:
a = b cos γ + c cos β
b = a cos γ + c cos α
c = a cos β + b cos α
Формулы для вычисления длин сторон треугольника
Медианы треугольника
Свойства медиан треугольника:
В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)
Медиана треугольника делит треугольник на две равновеликие части
Треугольник делится тремя медианами на шесть равновеликих треугольников.
Формулы медиан треугольника
Формулы медиан треугольника через стороны
ma = 1 2 √ 2 b 2 +2 c 2 — a 2
mb = 1 2 √ 2 a 2 +2 c 2 — b 2
mc = 1 2 √ 2 a 2 +2 b 2 — c 2
Биссектрисы треугольника
Свойства биссектрис треугольника:
Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника
Угол между биссектрисами внутреннего и внешнего углов треугольника при одной вершине равен 90°.
Формулы биссектрис треугольника
Формулы биссектрис треугольника через стороны:
la = 2√ bcp ( p — a ) b + c
lb = 2√ acp ( p — b ) a + c
lc = 2√ abp ( p — c ) a + b
где p = a + b + c 2 — полупериметр треугольника
Формулы биссектрис треугольника через две стороны и угол:
la = 2 bc cos α 2 b + c
lb = 2 ac cos β 2 a + c
lc = 2 ab cos γ 2 a + b
Высоты треугольника
Свойства высот треугольника
Формулы высот треугольника
ha = b sin γ = c sin β
hb = c sin α = a sin γ
hc = a sin β = b sin α
Окружность вписанная в треугольник
Свойства окружности вписанной в треугольник
Формулы радиуса окружности вписанной в треугольник
r = ( a + b — c )( b + c — a )( c + a — b ) 4( a + b + c )
Окружность описанная вокруг треугольника
Свойства окружности описанной вокруг треугольника
Формулы радиуса окружности описанной вокруг треугольника
R = S 2 sin α sin β sin γ
R = a 2 sin α = b 2 sin β = c 2 sin γ
Связь между вписанной и описанной окружностями треугольника
Средняя линия треугольника
Свойства средней линии треугольника
MN = 1 2 AC KN = 1 2 AB KM = 1 2 BC
MN || AC KN || AB KM || BC
Периметр треугольника
Периметр треугольника ∆ ABC равен сумме длин его сторон
Формулы площади треугольника
Формула Герона
| S = | a · b · с |
| 4R |
Равенство треугольников
Признаки равенства треугольников
Первый признак равенства треугольников — по двум сторонам и углу между ними
Второй признак равенства треугольников — по стороне и двум прилежащим углам
Третий признак равенства треугольников — по трем сторонам
Подобие треугольников
∆MNK => α = α 1, β = β 1, γ = γ 1 и AB MN = BC NK = AC MK = k ,
где k — коэффициент подобия
Признаки подобия треугольников
Первый признак подобия треугольников
Второй признак подобия треугольников
Третий признак подобия треугольников
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.