Отношением эквивалентности на множестве прямых пространства являются отношения параллельны (8 видео)

Свойства отношений на множестве

Отношение R на множестве Х называется рефлексивным, если о каждом элементе множества Х можно сказать, что он находится в отношении R с самим собой: хRх. Если отношение рефлексивно, то в каждой вершине графа имеется петля. И обратно, граф, каждая вершина которого содержит петлю, представляет собой граф рефлексивного отношения.

Примерами рефлексивных отношений являются и отношение «кратно» на множестве натуральных чисел (каждое число кратно самому себе), и отношение подобия треугольников (каждый треугольник подобен самому себе), и отношение «равенства» (каждое число равно самому себе) и др.

Существуют отношения, не обладающие свойством рефлексивности, например, отношение перпендикулярности отрезков: ab, ba (нет ни одного отрезка, о котором можно сказать, что он перпендикулярен самому себе). Поэтому на графе данного отношения нет ни одной петли.

Не обладает свойством рефлексивности и отношение «длиннее» для отрезков, «больше на 2» для натуральных чисел и др.

Отношение R на множестве Х называется антирефлексивным, если для любого элемента из множества Х всегда ложно хRх: .

Существуют отношения, не являющиеся ни рефлексивными, ни антирефлексивными. Примером такого отношения может служить отношение «точка х симметрична точке у относительно прямой l», заданное на множестве точек плоскости. Действительно, все точки прямой l симметричны сами себе, а точки, не лежащие на прямой l, себе не симметричны.

Отношение R на множестве Х называется симметричным, если выполняется условие: из того, что элемент х находится в отношении с элементом y, следует, что и элемент y находится в отношении R с элементом х: xRyyRx .

Граф симметричного отношения обладает следующей особенностью: вместе с каждой стрелкой, идущей от х к y, граф содержит стрелку, идущую от y к х (рис. 35).

Примерами симметричных отношений могут быть следующие: отношение «параллельности» отрезков, отношение «перпендикулярности» отрезков, отношение «равенства» отрезков, отношение подобия треугольников, отношение «равенства» дробей и др.

Существуют отношения, которые не обладают свойством симметричности.

Действительно, если отрезок х длиннее отрезка у, то отрезок у не может быть длиннее отрезка х. Граф этого отношения обладает особенностью: стрелка, соединяющая вершины, направлена только в одну сторону.

Отношение R называют антисимметричным, если для любых элементов х и y из истинности xRy следует ложность yRx: : xRyyRx.

Кроме отношения «длиннее» на множестве отрезков существуют и другие антисимметричные отношения. Например, отношение «больше» для чисел (если х больше у, то у не может быть больше х), отношение «больше на» и др.

Существуют отношения, которые не обладают ни свойством симметричности, ни свойством антисимметричности.

Отношение R на множестве Х называют транзитивным, если из того, что элемент х находится в отношении R с элементом y, а элемент y находится в отношении R с элементом z, следует, что элемент х находится в отношении R с элементом z: xRy и yRzxRz.

Граф транзитивного отношения с каждой парой стрелок, идущих от х к y и от y к z, содержит стрелку, идущую от х к z.

Свойством транзитивности обладает и отношение «длиннее» на множестве отрезков: если отрезок а длиннее отрезка b, отрезок b длиннее отрезка с, то отрезок а длиннее отрезка с. Отношение «равенства» на множестве отрезков также обладает свойством транзитивности: (а=b, b=с)(а=с).

Существуют отношения, которые не обладают свойством транзитивности. Таким отношением является, например, отношение перпендикулярности: если отрезок а перпендикулярен отрезку b, а отрезок b перпендикулярен отрезку с, то отрезки а и с не перпендикулярны!

Существует еще одно свойство отношений, которое называется свойством связанности, а отношение, обладающее им, называют связанным.

Отношение R на множестве Х называется связанным, если для любых элементов х и y из данного множества выполняется условие: если х и y различны, то либо х находится в отношении R с элементом y, либо элемент y находится в отношении R с элементом х. С помощью символов это определение можно записать так: xy xRy или yRx.

Например, свойством связанности обладает отношение «больше» для натуральных чисел: для любых различных чисел х и y можно утверждать, либо x>y, либо y>x.

На графе связанного отношения любые две вершины соединены стрелкой. Справедливо и обратное утверждение.

Существуют отношения, которые не обладают свойством связанности. Таким отношением, например, является отношение делимости на множестве натуральных чисел: можно назвать такие числа х и y, что ни число х не является делителем числа y, ни число y не является делителем числа х (числа 17 и 11, 3 и 10 и т.д.).

Рассмотрим несколько примеров. На множестве Х= задано отношение «число х кратно числу y». Построим граф данного отношения и сформулируем его свойства.

Про отношение равенства дробей говорят, оно является отношением эквивалентности.

Отношение R на множестве Х называется отношением эквивалентности, если оно одновременно обладает свойством рефлексивности, симметричности и транзитивности.

Примерами отношений эквивалентности могут служить: отношения равенства геометрических фигур, отношение параллельности прямых (при условии, что совпадающие прямые считаются параллельными).

В рассмотренном выше отношении «равенства дробей», множество Х разбилось на три подмножества: <; ; >, <; >, <>. Эти подмножества не пересекаются, а их объединение совпадает с множеством Х, т.е. имеем разбиение множества на классы.

Итак, если на множестве Х задано отношение эквивалентности, то оно порождает разбиение этого множества на попарно непересекающиеся подмножества – классы эквивалентности.

Так, мы установили, что отношению равенства на множестве
Х= <;; ; ; ; > соответствует разбиение этого множества на классы эквивалентности, каждый из которых состоит из равных между собой дробей.

Принцип разбиения множества на классы при помощи некоторого отношения эквивалентности является важным принципом математики. Почему?

Во-первых, эквивалентный – это значит равносильный, взаимозаменяемый. Поэтому элементы одного класса эквивалентности взаимозаменяемы. Так, дроби, оказавшиеся в одном классе эквивалентности <; ; >, неразличимы с точки зрения отношения равенства, и дробь может быть заменена другой, например . И эта замена не изменит результата вычислений.

Во-вторых, поскольку в классе эквивалентности оказываются элементы, неразличимые с точки зрения некоторого отношения, то считают, что класс эквивалентности определяется любым своим представителем, т.е. произвольным элементом класса. Так, любой класс равных дробей можно задать, указав любую дробь, принадлежащую этому классу. Определение класса эквивалентности по одному представителю позволяет вместо всех элементов множества изучать совокупность представителей из классов эквивалентности. Например, отношение эквивалентности «иметь одинаковое число вершин», заданное на множестве многоугольников, порождает разбиение этого множества на классы треугольников, четырехугольников, пятиугольников и т.д. свойства, присущие некоторому классу, рассматриваются на одном его представителе.

В-третьих, разбиение множества на классы с помощью отношения эквивалентности используется для введения новых понятий. Например, понятие «пучок прямых» можно определить как то общее, что имеют параллельные прямые между собой.

Другим важным видом отношений являются отношения порядка. Рассмотрим задачу. На множестве Х=<3, 4, 5, 6, 7, 8, 9, 10> задано отношение «иметь один и тот же остаток при делении на 3». Это отношение порождает разбиение множества Х на классы: в один попадут все числа, при делении которых на 3 получается в остатке 0 (это числа 3, 6, 9). Во второй – числа, при делении которых на 3 в остатке получается 1 (это числа 4, 7, 10). В третий попадут все числа, при делении которых на 3 в остатке получается 2 (это числа 5, 8). Действительно, полученные множества не пересекаются и их объединение совпадает с множеством Х. Следовательно, отношение «иметь один и тот же остаток при делении на 3», заданное на множестве Х, является отношением эквивалентности.

Возьмем еще пример: множество учащихся класса можно упорядочить по росту или возрасту. Заметим, что это отношение обладает свойствами антисимметричности и транзитивности. Или всем известен порядок следования букв в алфавите. Его обеспечивает отношение «следует».

Отношение R на множестве Х называется отношением строгого порядка, если оно одновременно обладает свойствами антисимметричности и транзитивности. Например, отношение «х Просмотров 153 477 Комментариев 0

Содержание

Отношение эквивалентности
1. Бинарные отношения
2. Операции над отношениями
3. Свойства отношений
4. Инвариантность отношений
5. Отношение эквивалентности
6. Классы эквивалентности
Литература
💥 Видео

Видео:3.3 Отношение эквивалентности | Роман Попков | ИТМОСкачать

Отношение эквивалентности

Важным видом бинарного отношения является отношение эквивалентности.

Определение 5.1. Бинарное отношение a на множестве X называется отношением эквивалентности на X, если a рефлексивно, симметрично и транзитивно.

Отношение эквивалентности часто обозначают символами

, .

Примерами отношения эквивалентности служат:

· отношение тождества I_X = <(a, a)|a X> на непустом множестве X;

· отношение параллельности на множестве прямых плоскости;

· отношение подобия на множестве фигур плоскости;

· отношение равносильности на множестве уравнений;

· отношение «иметь одинаковые остатки при делении на фиксированное натуральное число m» на множестве целых чисел. Это отношение в математике называют отношением сравнимости по модулю m и обозначают a b (mod m);

· отношение «принадлежать одному виду» на множестве животных;

· отношение «быть родственниками» на множестве людей;

· отношение «быть одного роста» на множестве людей;

· отношение «жить в одном доме» на множестве людей.

Отношения «жить на одной улице», «быть похожими» на множестве людей отношениями эквивалентности не являются, так как не обладают свойством транзитивности.

Из перечисленных выше свойств бинарных отношений следует, что пересечение отношений эквивалентности является отношением эквивалентности.

Классы эквивалентности

С отношением эквивалентности тесно связано разбиение множества на классы.

Определение 6.1. Система непустых подмножеств

множества M называется разбиением этого множества, если

M = M₁ M₂ …

и при i j

M_i M_j =O.

Сами множества M₁, M₂, … называются при этом классами данного разбиения.

Примерами разбиений служат:

· разложение всех многоугольников на группы по числу вершин — треугольники, четырехугольники, пятиугольники и т. д.;

· разбиение всех треугольников по свойствам углов (остроугольные, прямоугольные, тупоугольные);

· разбиение всех треугольников по свойствам сторон (разносторонние, равнобедренные, равносторонние);

· разбиение всех треугольников на классы подобных треугольников;

· разбиение множества всех учащихся данной школы по классам.

Широкое применение отношений эквивалентности в современной науке связано с тем, что всякое отношение эквивалентности осуществляет разбиение множества, в котором оно определено, на классы, обычно принимаемые за новые объекты. Другими словами с помощью отношений эквивалентности порождаются новые объекты, понятия.

Так, например, отношение сонаправленности лучей разбивает множество всех лучей плоскости или пространства на классы сонаправленных лучей. Каждый из этих классов лучей называется направлением. Таким образом, интуитивное понятие направления получает точное математическое описание как класс разбиения множества лучей с помощью отношения эквивалентности.

О подобных фигурах обычно говорят, что они имеют одинаковую форму. Но что такое форма геометрической фигуры? Интуитивно ясно, что это то общее, что объединяет подобные фигуры. С помощью отношения эквивалентности удается это интуитивное понятие перевести в точное математическое. Отношение подобия, являясь отношением эквивалентности, разбивает множество фигур на классы подобных фигур. Каждый такой класс можно назвать формой. Тогда выражение «две одинаковые фигуры имеют одинаковую форму» имеет следующий точный смысл «две подобные фигуры принадлежат одной форме».

Отношения эквивалентности встречаются всюду, где осуществляются разбиения множеств на классы. Мы часто пользуемся ими, не замечая этого.

Приведем элементарный пример. Когда дети играют со множеством разноцветных игрушек (например, с блоками Дьенеша) и решают задачу разложить игрушки по цветам, то они пользуются отношением «иметь один цвет». Полученные в результате классы одноцветных фигур воспринимаются детьми как новые понятия: красные, желтые, синие и т. д.

Аналогично в результате решения задачи разложения блоков по форме дети получают классы, каждый из которых воспринимается как форма: прямоугольные, круглые, треугольные и т. д.

Связи между отношениями эквивалентности, определенными на множестве M, и разбиениями множества M на классы описываются в следующих двух теоремах.

Теорема 6.1. Всякое разбиение непустого множества M на классы определяет (индуцирует) на этом множестве отношение эквивалентности такое, что:

· всякие два элемента одного класса находятся в отношении a;

· всякие два элемента различных классов не находятся в отношении a.

Доказательство. Пусть имеется некоторое разбиение непустого множества M. Определим бинарное отношение a следующим образом:

xay ( K )( x K&y K).

То есть два элемента x и y aиз множества M связаны отношением a в том и только в том случае, если в разбиении найдется такой класс K, которому одновременно принадлежат элементы x и y.

Так определенное отношение a, очевидно, рефлексивно и симметрично. Докажем транзитивность отношения a. Пусть xay и xaz. Тогда по определению в существуют классы K₁ и K₂ такие, что x, y K₁ и y, z K₂. Так как различные классы в разбиении не имеют общих элементов, то K₁ = K₂, то есть x, z K₁. Поэтому xaz, что и требовалось доказать.

Теорема 6.2. Всякое отношение эквивалентности в непустом множестве M порождает разбиение этого множества на классы эквивалентности такое, что

· всякие два элемента одного класса находятся в отношении a;

· всякие два элемента различных классов не находятся в отношении a.

Доказательство. Пусть a — некоторое отношение эквивалентности на множестве M. Каждому элементу x из поставим в соответствие подмножество [x] множества M, состоящее из всех элементов y, находящихся в отношении a с элементом x:

Система подмножеств [x], образует разбиение множества M. Действительно, во-первых, каждое подмножество [x] O , так как в силу рефлексивности отношения a x [x].

Во-вторых, два различных подмножества [x] и [y] не имеют общих элементов. Рассуждая от противного, допустим существование элемента z такого, что z [x] и z [y]. Тогда zax и zay. Поэтому для любого элемента a [x] из aa x, zax и zay в силу симметричности и транзитивности отношения a вытекает aay, то есть a [y]. Следовательно, [x] [y]. Аналогично получаем, что [y] [x]. Полученные два включения влекут равенство [x] = [y], противоречащее предположению о несовпадении подмножеств [x] и [y]. Таким образом,

[x] y] = O.

В-третьих, объединение всех подмножеств [x] совпадает со множеством M, ибо для любого элемента x M выполняется условие x [x].

Итак, система подмножеств [x], образует разбиение множества M. Несложно показать, что построенное разбиение удовлетворяет условиям теоремы.

Разбиение множества M, обладающее свойствами, указанными в теореме, называется фактор-множеством множества M по отношению a и обозначается M/a.

Подведем некоторые итоги. Мы убедились, что задание эквивалентности a на множестве M равносильно заданию некоторого разбиения этого множества. Иными словами, определить некоторое отношение эквивалентности между элементами множества M — это означает разбить множество M на непересекающиеся классы и считать эквивалентными те и только те элементы, которые попали в один и тот же класс. На фактор-множество M/a можно смотреть как на совокупность классов элементов из M, неразличимых «с точностью до эквивалентности a». Построение фактор-множества M/a называют иногда факторизацией множества по отношению a.

Отношение эквивалентности лежит в основе всевозможных классификаций. При классификации некоторого множества в нем задают одно или несколько отношений эквивалентности и рассматривают классы эквивалентности, связанные с этими отношениями.

При иерархической классификации все множество разлагается на классы эквивалентности, после чего каждый класс разлагается на классы эквивалентности по другому отношению и т. д. Такая классификация применяется, например, в биологии (царства живых существ, типы, классы, отряды, роды, виды). В математике иерархическая классификация используется, например, при классификации линий второго порядка.

Другой вид классификации основан на том, что указывается несколько свойств (например форма, цвет, размер и т. д.), каждое из которых может принимать несколько значений (например, квадрат, круг, шестиугольник или красный зеленый, синий и т. д.). После этого каждый класс характеризуется значениями, принимаемыми на нем данными свойствами (например, зеленые маленькие квадраты). В библиотеках множество всех книг разбивают на книги по математике, физике, химии, истории и т. д. Далее книги по математике делят на книги по алгебре, геометрии, математическому анализу и т. д. В математике такой вид классификации используется, например, при классификации многоугольников, с одной стороны, по числу сторон, а с другой — по признаку правильности или неправильности.

Так как пересечение отношений эквивалентности является отношением эквивалентности, то это позволяет сводить классификацию по нескольким признакам к классификации по одному сложному признаку.

Более подробное исследование вопросов, связанных с классификацией, будет рассмотрено в специальной лекции.

Литература

1. Шрейдер Ю. А. Равенство, сходство, порядок. — М.: Наука, 1971.

2. Розен В. В. Цель — оптимальность — решение (математические модели принятия оптимальных решений). — М.: Радио и связь, 1982.

3. Столяр А. А., Рогановский Н. М. Основы современной школьной математики. Ч. 1. Язык. Множества. Отношения. Функции. Математические структуры. — Минск: Нар. Асвета, 1975.

4. Мальцев А. И. Алгебраические системы. М.: Наука, 1970.

Видео:Бинарные отношения. Как определить свойства?Скачать

1. Бинарные отношения

Бинарные отношения служат простым и удобным аппаратом для весьма широкого круга задач. Язык бинарных и n-арных отношений используется во многих прикладных (для математики) областях, например, таких как математическая лингвистика, математическая биология, математическая теория баз данных. Широкое использование языка бинарных отношений легко объясняется — геометрический аспект теории бинарных отношений есть попросту теория графов.

Введем необходимые определения.

Определение 1.1. Декартовым произведением множеств X и Y называется множество XxY всех упорядоченных пар (x, y) таких, что x X, y Y.

Определение 1.2. Соответствием между множествами X и Y (или соответствием из X в Y) называется любое подмножество декартова произведения XxY. Если множества X и Y совпадают, то соответствие между множествами X и Y называют также бинарным отношением на множестве X.

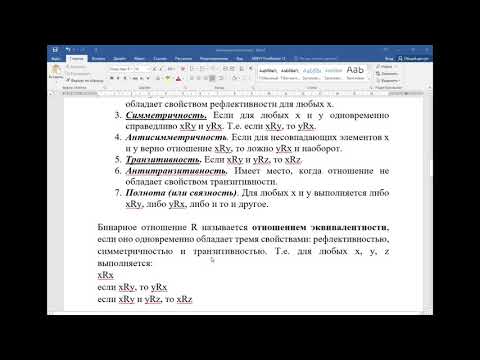
Отметим, что обычно соответствия задаются не путем указания подмножества a декартова произведения XxY, а путем указания свойства пар (x, y), принадлежащих этому подмножеству

a . Например, отношение a = <(4, 4), (3, 3), (2, 2), (4, 2)> на множестве X = <4, 3, 2> можно определить как свойство «Делится» на этом подмножестве целых чисел.

Хорошо известными примерами отношений из школьного курса математики являются:

на множестве целых чисел Z отношения «делится», «делит», «равно», «больше», «меньше», «взаимно просты»;
на множестве прямых пространства отношения «параллельны», «взаимно перпендикулярны», «скрещиваются», «пересекаются», «совпадают»;
на множестве окружностей плоскости «пересекаются», «касаются», «концентричны».

Факт принадлежности кортежа (x, y) соответствию a , часто обозначают с помощью так называемой инфиксной формы записи: x a y. Типичными примерами таких записей из курса математики являются: x > y, a = b, 8 4, m||l, a b и т. п.

Отношения могут задаваться формулами:

формулы

y = x 2 +5x — 6 или

задают бинарные отношения на множестве действительных чисел;

формула

задает бинарное отношение на множестве людей. Этому отношению принадлежит любая пара людей, между которыми существует любовь.

Задание отношений в виде формул достаточно широко распространено. Об этом свидетельствуют многочисленные надписи на деревьях заборах или стенах домов типа:

«Вася + Таня = любовь»,

увековечивающие принадлежность конкретной пары (Вася, Таня) отношению «любовь».

Рассмотрим еще три формы представления бинарных отношений: матричное представление и два графических представления. В качестве носителя отношения для иллюстрирующих примеров будем использовать множество X = <a, b, c, d, e>.

Вначале рассмотрим метод, восходящий к аналитической геометрии. Начертим пару взаимно перпендикулярных осей (OX — горизонтальная ось, а OY — вертикальная ось) и на каждой отметим точки, представляющие элементы множества X (рис. 1).

Рис. 1. Координатная сетка

Считая метки a, b, c, d, e координатами точек на горизонтальной и вертикальной осях, отметим на плоскости точки с координатами (x, y) такими, что (x, y) . На рисунке 2 изображено множество точек, соответствующее отношению a = <(a, b), (a, c), (b, d), (c, e), (e,b), (e, e)>.

Рис. 2. Бинарное отношение a

Другой широко распространенный способ представления отношений основан на использовании ориентированных графов. При таком представлении элементы множества X изображаются вершинами графа (точками плоскости), а элементы (x, y) отношения a дугами (стрелками), соединяющими первую компоненту x отношения со второй компонентой y. Граф бинарного отношения a изображен на рисунке 3.

Рис. 3. Граф бинарного отношения

Для бинарных отношений, определенных на конечных множествах, часто используется матричный способ задания. Пусть на некотором конечном множестве X задано отношение a . Упорядочим каким-либо образом элементы множества X = <x₁, x₂, . x_n> и определим матрицу отношения A = [a_ij] следующим образом:

Таким образом, матрица отношения a , представленного графом на рисунке 3, имеет вид

Часто матрицу отношения называют булевой, чтобы подчеркнуть, что ее элементами являются только нули и единицы.

Видео:3.2 Бинарные отношения | Роман Попков | ИТМОСкачать

2. Операции над отношениями

Так как бинарные отношения являются множествами, то к ним применимы все понятия, которые вводятся для множеств: понятие равенства, включения, а также операции пересечения, объединения и дополнения. В этом разделе мы будем считать, что все отношения заданы на одном и том же множестве X.

Пусть a и b — два бинарных отношения на множестве X. Каждому из них соответствует некоторое множество пар (подмножества и ).

Определение 2.1. Пересечением отношений a и b , заданных на множестве X, называется отношение такое, что:

Пример 2.1. Пересечением отношений «не меньше» и «не равно», определенных на множестве действительных чисел R, является отношение «строго больше»:

Определение 2.2. Объединением отношений a и b , заданных на множестве X, называется отношение , такое, что:

является отношение «быть ребенком».

Определение 2.3. Разностью отношений a и b , заданных на множестве X, называется отношение a b , такое, что:

Пример 2.3. Разностью отношений «не меньше» и «не больше» на R является отношение «больше»:

Пример 2.4. Разностью отношений «быть ребенком» и «быть дочерью», определенных на множестве всех людей, является отношение «быть сыном».

Определение 2.4. Дополнением отношения a , определенного на множестве X, называется отношение, определяемое подмножеством пар из XxX, не входящих в :

x y .

Пример 2.5. Дополнением отношения «не меньше» на R является отношение «не меньше»:

Отметим, что приведенные выше определения являются просто перефразировками соответствующих определений для обычных множеств и все свойства теоретико-множественных операций пересечения, объединения и дополнения, имеющие место для произвольных множеств, выполняются и для отношений.

Кроме теоретико-множественных операций для отношений вводятся некоторые дополнительные операции, которые связаны с их специфической структурой. Мы рассмотрим две такие операции.

Определение 2.5. Если в каждой упорядоченной паре, принадлежащей отношению a , поменять местами первую и вторую компоненты, то получим новое отношение, которое называется обратным для отношения a и обозначается через a -1 :

Пример 2.6. Обратным для отношения «не меньше» на множестве действительных чисел R является отношение «меньше»:

Пример 2.7. Обратным для отношения «быть родителем» на множестве людей является отношение «быть ребенком».

Граф отношения a -1 получается из графа отношения переориентацией всех дуг (рис. 4).

(а) Отношение a (б) Отношение a -1

Рис. 4. Графы отношений a и a -1

Если отношение задано с помощью булевой матрицы, то, поменяв в ней местами строки и столбцы, получим булеву матрицу отношения a -1 (рис 5).

(а) Матрица отношения a (б) Матрица отношения a -1

Рис. 5. Матрицы отношений a и a -1

Определение 2.6. Произведением или композицией отношений a и b , заданных на множестве X, называется отношение a ° b , состоящее из таких кортежей (x, z), для которых существует элемент , удовлетворяющий условию и :

Пример 2.8. Произведением отношений «быть братом» и «быть отцом» является отношение «быть братом одного из родителей», т. е. «быть дядей».

Если отношения a и b на некотором множестве X заданы с помощью графов, то принадлежность пары (x, z) к отношению a ° b означает, что из вершины x в вершину z можно попасть точно за два шага, причем первый из них делается по дуге отношения a , а второй — по дуге отношения b .

На рисунке 6 изображены графы, представляющие отношения a (точечные дуги) и b (пунктирные дуги), и графы, представляющие произведения отношений a ° b и b ° a .

(а) Графы отношений a и b (б) Граф отношения a ° b

(в) Граф отношения a ° b

Рис. 6. Пример произведения отношений ( a ° b b ° a )

Пример, приведенный на рисунке 6, показывает, что для произведения отношений коммутативный закон не выполняется.

Для выражения матрицы произведения двух отношений a и b , заданных булевыми матрицами и , введем понятие «булево сложение» , определив его следующим образом:

0 0 = 0, 0 1 = 1, 1 0 = 1, 1 1 = 1.

c_ik = a_i1 b_1k … a_in b_nk

Пример 2.9. Вычислим матрицы произведений a ° b и b ° a отношений a и b , представленных графами на рисунке 6.

Для этого перемножим соответствующие матрицы M a и M b (строки и столбцы матриц упорядочены в соответствии с алфавитным порядком букв a, b, c, d, обозначающих вершины графа).

Определим еще одну унарную операцию над отношением.

Определение 2.7. Транзитивным замыканием отношения a называется бинарное отношение такое, что x y тогда и только тогда, когда существует такая цепочка элементов из X:

что между соседями в этой цепочке выполнено отношение a :

Пример 2.10. На рисунке 7 изображены графы, представляющие отношение a и его транзитивное замыкание .

Рис. 7. Транзитивное замыкание отношения a

В матричной форме операция транзитивного замыкания отношения a выражается через объединение степеней матрицы M a отношения a :

В приведенной формуле объединение матриц понимается следующим образом:

Видео:Интуитивная топология | теоретикомнож. вопр. | бинарные отношения | отношение эквивалентности | 1Скачать

3. Свойства отношений

Очевидно, что произвольные бинарные отношения изучать в общем плане не особенно интересно, о них можно сказать очень мало. Однако, если отношения удовлетворяют некоторым дополнительным условиям, относительно них можно делать более содержательные утверждения. В этом разделе мы рассмотрим некоторые из основных свойств бинарных отношений.

Определение 3.1. Бинарное отношение a на множестве X называется рефлексивным, если для любого элемента a X выполняется условие a a a:

( a X) a a a.

Если отношение представлено с помощью графа, то рефлексивность этого отношения означает, что в каждой вершине графа обязательно имеется петля.

Для отношения, заданного с помощью булевой матрицы его рефлексивность равносильна тому, что по главной диагонали этой матрицы (идущей из ее левого верхнего угла в правый нижний) стоят только символы 1.

Определение 3.2. Бинарное отношение a на X называется антирефлексивным, если ни для одного a X не выполняется условие a a a:

( a X) .

Обозначим через I_x отношение на множестве X, состоящее из пар вида (a, a), где a X:

I_x = <(a, a)| a X>.

Отношение I_x обычно называют диагональю множества X или отношением тождества на X.

Очевидно, что отношение a на множестве X рефлексивно, если диагональ I_x является подмножеством множества a :

I_x a .

Отношение антирефлексивно, если диагональ I_x и отношение a не имеют ни одного общего элемента:

I_x a = O.

Определение 3.3. Бинарное отношение a на множестве X называется симметричным, если из a a b следует b a a:

( a, b X)(a a b b a a).

Примерами симметричных отношений являются:

отношение перпендикулярности на множестве прямых;
отношение касания на множестве окружностей;
отношение «быть похожим» на множестве людей;
отношение «иметь одинаковый пол» на множестве животных.

Отношение «x брат y» на множестве всех людей не является симметричным. В то же время отношение «x брат y» на множестве мужчин симметричным является.

В графе симметричного отношения для каждой дуги из вершины x в вершину y имеется дуга из y в x. Поэтому симметричные отношения можно представлять графами с неориентированными ребрами. При этом каждая пара ориентированных ребер xy и yx заменяется одним неориентированным ребром.

На рисунке 8 представлено отношение

с помощью ориентированного и неориентированного графов.

Рис. 8. Представление симметричного отношения с помощью
ориентированного (a) и неориентированного (b) графов

Матрица симметричного отношения симметрична относительно главной диагонали.

Теорема 3.1. Объединение и пересечение любого семейства симметричных отношений снова являются симметричными отношениями.

Определение 3.4. Бинарное отношение a на множестве X называется антисимметричным, если для любых различных элементов a и b условия a a b и b a a не выполняются одновременно:

( a, b X) (a a b & b a a a = b).

Например, отношение «делится» на множестве натуральных чисел является антисимметричным, так как из a b и b a следует, что a = b. Однако на множестве целых чисел отношение «делится» антисимметричным не является, так как (-2) 2 и 2 (-2), но

-2 2.

Отношения «выше», «тяжелее», «старше» антисимметричны на множестве людей. Отношение «быть сестрой» на множестве всех людей антисимметричным не является.

В графе антисимметричного отношения две различные вершины могут быть соединены не более чем одной дугой.

Определение 3.5. Бинарное отношение a на множестве X называется транзитивным, если для любых трех элементов a, b, c X из a a b и b a c следует a a c:

( a, b, c X) (a a b & b a c a a c).

Примерами транзитивных отношений служат:

отношение «делится» на множестве действительных чисел;
отношение «больше» на множестве действительных чисел;
отношение «старше» на множестве людей игрушек;
отношение «иметь одинаковый цвет» на множестве детских игрушек;

д) отношение «быть потомком» на множестве людей.

Феодальное отношение «быть вассалом» не является транзитивным. Это в частности подчеркивается в некоторых учебниках истории: «вассал моего вассала не мой вассал».

Отношение «быть похожим» на множестве людей не обладает свойством транзитивности.

Для произвольного отношения a можно найти минимальное транзитивное отношение b

такое, что a b . Минимальность отношения понимается в том смысле, что для любого транзитивного отношения g из a g следует b g . Таким отношением является транзитивное замыкание отношения a .

Пример 3.1. Транзитивным замыканием бинарного отношения на множестве людей «быть ребенком» является отношение «быть потомком».

Теорема 3.2. Для любого отношения транзитивное замыкание равно пересечению всех транзитивных отношений, включающих в качестве подмножества.

Определение 3.6. Бинарное отношение a на множестве X называется связным, если для любых двух различных элементов a и b имеет место a a b, либо b a a:

( a, b, c X)(a b a a b b a a).

Примером связного отношения является отношение «больше» на множестве действительных чисел. Отношение «делится» на множестве целых чисел связным не является.

Видео:Бинарные отношения видеолекцияСкачать

4. Инвариантность отношений

В этом параграфе мы перечислим некоторые случаи, когда те или иные свойства отношений сохраняются при выполнении над ними операций [1].

Теорема 4.1. Если отношения a и b рефлексивны, то рефлексивны и следующие отношения:

a b , b a , a -1 , a°b , .

Теорема 4.2. Если отношения a и b антирефлексивны, то антирефлексивны и следующие отношения:

a b , b a , a -1 .

Теорема 4.3. Если отношения a и b симметричны, то симметричны и следующие отношения:

a b , b a , a -1 .

Теорема 4.4. Чтобы произведение a°b симметричных отношений a и b было симметрично, необходимо и достаточно, чтобы отношения и коммутировали:

Теорема 4.5. Если отношения a и b антисимметричны, то антисимметричны и следующие отношения:

a b , a -1

Теорема 4.6. Если отношения a и b транзитивны, то транзитивны и следующие отношения:

a b , a -1 , .

Другие интересные свойства отношений описаны в [1, 2].

Видео:Математика это не ИсламСкачать

5. Отношение эквивалентности

Важным видом бинарного отношения является отношение эквивалентности.

Отношение эквивалентности часто обозначают символами

, .

Примерами отношения эквивалентности служат:

отношение тождества I_X = <(a, a)|aX> на непустом множестве X;
отношение параллельности на множестве прямых плоскости;
отношение подобия на множестве фигур плоскости;
отношение равносильности на множестве уравнений;
отношение «иметь одинаковые остатки при делении на фиксированное натуральное число m» на множестве целых чисел. Это отношение в математике называют отношением сравнимости по модулю m и обозначают ab(mod m);
отношение «принадлежать одному виду» на множестве животных;
отношение «быть родственниками» на множестве людей;
отношение «быть одного роста» на множестве людей;
отношение «жить в одном доме» на множестве людей.

Видео:Проверяем свойства отношенийСкачать

6. Классы эквивалентности

С отношением эквивалентности тесно связано разбиение множества на классы.

Определение 6.1. Система непустых подмножеств

множества M называется разбиением этого множества, если

M = M₁ M₂ …

и при i j

M_i M_j =O.

Сами множества M₁, M₂, … называются при этом классами данного разбиения.

Примерами разбиений служат:

разложение всех многоугольников на группы по числу вершин — треугольники, четырехугольники, пятиугольники и т. д.;
разбиение всех треугольников по свойствам углов (остроугольные, прямоугольные, тупоугольные);
разбиение всех треугольников по свойствам сторон (разносторонние, равнобедренные, равносторонние);
разбиение всех треугольников на классы подобных треугольников;
разбиение множества всех учащихся данной школы по классам.

всякие два элемента одного класса находятся в отношении a ;
всякие два элемента различных классов не находятся в отношении a .

x a y ( K )( x K&y K).

То есть два элемента x и y a из множества M связаны отношением a в том и только в том случае, если в разбиении найдется такой класс K, которому одновременно принадлежат элементы x и y.

Так определенное отношение a , очевидно, рефлексивно и симметрично. Докажем транзитивность отношения a . Пусть x a y и x a z. Тогда по определению в существуют классы K₁ и K₂ такие, что x, y K₁ и y, z K₂. Так как различные классы в разбиении не имеют общих элементов, то K₁ = K₂, то есть x, z K₁. Поэтому x a z, что и требовалось доказать.

всякие два элемента одного класса находятся в отношении a ;
всякие два элемента различных классов не находятся в отношении a .

Во-вторых, два различных подмножества [x] и [y] не имеют общих элементов. Рассуждая от противного, допустим существование элемента z такого, что z [x] и z [y]. Тогда z a x и z a y. Поэтому для любого элемента a [x] из a a x, z a x и z a y в силу симметричности и транзитивности отношения a вытекает a a y, то есть a [y]. Следовательно, [x] [y]. Аналогично получаем, что [y] [x]. Полученные два включения влекут равенство [x] = [y], противоречащее предположению о несовпадении подмножеств [x] и [y]. Таким образом,

[x] y] = O.

Подведем некоторые итоги. Мы убедились, что задание эквивалентности a на множестве M равносильно заданию некоторого разбиения этого множества. Иными словами, определить некоторое отношение эквивалентности между элементами множества M — это означает разбить множество M на непересекающиеся классы и считать эквивалентными те и только те элементы, которые попали в один и тот же класс. На фактор-множество M/ a можно смотреть как на совокупность классов элементов из M, неразличимых «с точностью до эквивалентности a «. Построение фактор-множества M/ a называют иногда факторизацией множества по отношению a .

Более подробное исследование вопросов, связанных с классификацией, будет рассмотрено в специальной лекции.

Видео:ДМ. Бинарные отношения, часть 1. 22 сентября 2020 года.Скачать