Определите длину окружности монеты прокатив ее по линейке (6 видео)

Определите толщину монеты при помощи линейки.

Содержание

Ваш ответ
решение вопроса
Похожие вопросы
Определите длину окружности монеты двумя способами
Длина окружности
Длина окружности
Задачи на длину окружности
Задачи на площадь круга
Изучение способов нахождения длины окружности
Библиографическое описание:
Определите длину окружности монеты: 1) прокатив её по линейке» (рис. 17, а); 2) измерив диаметр монеты (рис. 17, б) и умножив его на число пи — 3,14. Сравните результаты измерений. В каком случае в проводили прямое измерение, в каком — косвенное
Ответы 2
Определите толщину монеты при помощи линейки.
Ваш ответ
решение вопроса
Похожие вопросы
🔥 Видео

Видео:+Как найти длину окружностиСкачать

Ваш ответ

Видео:КАК НАЙТИ ДИАМЕТР ОКРУЖНОСТИ, ЕСЛИ ИЗВЕСТНА ДЛИНА ОКРУЖНОСТИ? Примеры | МАТЕМАТИКА 6 классСкачать

решение вопроса

Видео:Длина окружности. Математика 6 класс.Скачать

Определите длину окружности монеты двумя способами

Видео:КАК НАЙТИ ДЛИНУ ОКРУЖНОСТИ, ЕСЛИ ИЗВЕСТЕН ДИАМЕТР ИЛИ РАДИУС? Примеры | МАТЕМАТИКА 6 классСкачать

Длина окружности

Видео:КАК ИЗМЕРИТЬ ДЛИНУ ОКРУЖНОСТИ? · ФОРМУЛА + примеры · Длина окружности как найти? Математика 6 классСкачать

Длина окружности

Длина любой окружности больше своего диаметра в одно и то же число раз, а именно, приблизительно в 3,14 раза. Для обозначения этой величины используется маленькая (строчная) греческая буква π (пи):

Таким образом, длину окружности (C) можно вычислить, умножив константу π на диаметр (D), или умножив π на удвоенный радиус, так как диаметр равен двум радиусам. Следовательно, формула длины окружности будет выглядеть так:

где C — длина окружности, π — константа, D — диаметр окружности, R — радиус окружности.

Так как окружность является границей круга, то длину окружности можно также назвать длиной круга или периметром круга.

Видео:Длина окружности. Площадь круга. 6 класс.Скачать

Задачи на длину окружности

Задача 1. Найти длину окружности, если её диаметр равен 5 см.

Решение: Так как длина окружности равна π умноженное на диаметр, то длина окружности с диаметром 5 см будет равна:

C ≈ 3,14 · 5 = 15,7 (см).

Задача 2. Найти длину окружности, радиус которой равен 3,5 м.

Решение: Сначала найдём диаметр окружности, умножив длину радиуса на 2:

теперь найдём длину окружности, умножив π на диаметр:

C ≈ 3,14 · 7 = 21,98 (м).

Задача 3. Найти радиус окружности, длина которой равна 7,85 м.

Решение: Чтобы найти радиус окружности по её длине, надо длину окружности разделить на 2π:

следовательно, радиус будет равен:

R	≈	7,85	=	7,85	= 1,25 (м).
		2 · 3,14		6,28

Видео:Длина окружности. Площадь круга - математика 6 классСкачать

Задачи на площадь круга

Задача 1. Найти площадь круга, если его радиус равен 2 см.

Решение: Так как площадь круга равна π умноженное на радиус в квадрате, то площадь круга с радиусом 2 см будет равна:

S ≈ 3,14 · 2 2 = 3,14 · 4 = 12,56 (см 2 ).

Ответ: 12,56 см 2 .

Задача 2. Найти площадь круга, если его диаметр равен 7 см.

Решение: Сначала найдём радиус круга, разделив его диаметр на 2:

теперь вычислим площадь круга по формуле:

S = πr 2 ≈ 3,14 · 3,5 2 = 3,14 · 12,25 = 38,465 (см 2 ).

Данную задачу можно решить и другим способом. Вместо того чтобы сначала находить радиус, можно воспользоваться формулой нахождения площади круга через диаметр:

S = π

D 2

≈ 3,14 ·

7 2

= 3,14 ·49=444

=	153,86	= 38,465 (см 2 ).
	4

Ответ: 38,465 см 2 .

Задача 3. Найти радиус круга, если его площадь равна 12,56 м 2 .

Решение: Чтобы найти радиус круга по его площади, надо площадь круга разделить π, а затем из полученного результата извлечь квадратный корень:

Видео:ПОГРЕШНОСТЬ ИЗМЕРЕНИЯ 7 класс относительная абсолютная погрешностьСкачать

Изучение способов нахождения длины окружности

Рубрика: Математика: алгебра и начала анализа, геометрия

Дата публикации: 29.12.2019 2019-12-29

Статья просмотрена: 2395 раз

Библиографическое описание:

Бородин, М. В. Изучение способов нахождения длины окружности / М. В. Бородин, О. Б. Никитина. — Текст : непосредственный // Юный ученый. — 2020. — № 1 (31). — С. 37-42. — URL: https://moluch.ru/young/archive/31/1837/ (дата обращения: 18.11.2021).

В своей повседневной жизни мы часто сталкиваемся с задачами, которые связаны с вычислением периметра, то есть суммы длин сторон различных геометрических фигур. В случае, если геометрическая фигура — многоугольник, нахождение его периметра не составляет особого труда: для этого достаточно с помощью линейки измерить длину каждой из сторон и сложить полученные результаты. Что же делать, если необходимо узнать длину окружности? Ответу на этот вопрос посвящена данная статья.

Окружность является самой распространённой кривой практически во всех областях человеческой деятельности. Форму окружности или круга мы встречаем повсюду: это и колесо машины, и линия горизонта, и диск Луны. Многие вещи, окружающие нас, имеют круглую форму, например: обруч, кольцо, мяч, тарелка.

В свободное время я люблю заниматься моделированием из бумаги, пластилина и, особенно, из деталей конструктора Лего. Иногда, для того чтобы подготовить нужную заготовку для модели, необходимо знать длину сторон фигуры, которую хочешь получить. Никогда эта задача не вызывала у меня затруднений, пока я не столкнулся с определением длины окружности.

В учебнике по геометрии 7 класса рассматривается вопрос определения длины окружности. Существует формула, при помощи которой решается эта задача. Мне стало интересно, а как же раньше, в древности, люди находили длину окружности, можно ли ее найти экспериментальным путем без помощи известной формулы, какая существует связь между размером окружности (диаметром) и длиной окружности, и какое практическое применение может иметь решение этой задачи.

Ещё в давние времена люди сталкивались с практическими задачами, для решения которых необходимо было уметь находить длину окружности. Например, для того чтобы изготовить металлический обод для колеса телеги, определить вместительность сосуда, при строительстве зданий, для изготовления ювелирных изделий, при пошиве одежды.

В источниках [1, 4] сказано, что уже 4 тысячи лет назад люди знали, что длина окружности примерно равна трём его диаметрам. В дальнейшем, более 2 тыс. лет назад, большой вклад в развитие геометрии, в том числе в изучение геометрических фигур — окружности и круга — внесли древнегреческий математик Евклид, а позже — Архимед.

Целью исследования является изучение различных способов нахождения длины окружности и получение взаимосвязи между диаметром окружности и её длиной.

Гипотеза исследования: формулу длины окружности можно получить самостоятельно экспериментальным путем.

Основные понятия

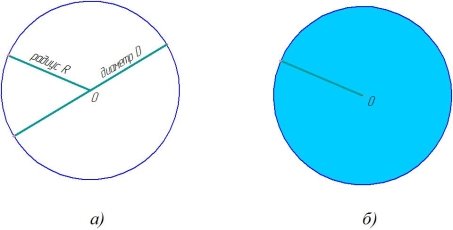
Окружность — это замкнутая плоская кривая линия, все точки которой находятся на одинаковом расстоянии от заданной точки О. Эта точка называется центром окружности (рисунок 1,а).

Круг — часть плоскости, ограниченная окружностью (рисунок 1,б).

Можно сказать, что окружность является границей круга.

Основные линии окружности — радиус и диаметр (рисунок 1,а).

Радиус R окружности — это отрезок, соединяющий центр О с любой точкой окружности.

Диаметр D окружности — отрезок, который соединяет две точки окружности и проходит через ее центр.

Рис. 1. Окружность и круг

Способы нахождения длины окружности

Рассмотрим некоторые возможные способы нахождения длины окружности.

Нахождение длины окружности с помощью нити

Когда я впервые задумался над решением данной задачи, первое и самое простое, что пришло на ум — это приложить нить к окружности, а затем при помощи линейки измерить ее длину. Подготовиться к эксперименту мне помог папа: он вырезал на станке металлические круги разных диаметров.

Проведем измерение круга диаметром 50 мм. Я обернул круг нитью, шариковой ручкой сделал отметки и при помощи линейки измерил длину нити между отметками (рисунок 2).

Длина нити оказалась равной 158 мм. При измерении я обратил внимание на то, что результат получается приблизительным, так как зависит от силы натяжения нити и ее толщины. И самое главное — не каждую окружность можно измерить таким способом.

То есть данный экспериментальный способ не решает поставленной задачи. Необходимо получить универсальную формулу, при помощи которой можно было бы найти длину окружности любого диаметра.

Рис. 2. Нахождение длины окружности с помощью нити

Нахождение длины окружности с помощью квадратов

Следующий способ, который я решил применить: представить окружность в виде квадрата (рисунок 3).

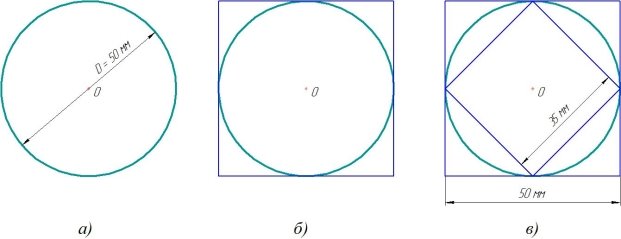
Продолжаем исследовать окружность диаметром 50 мм (рисунок 3,а).

Построим вокруг окружности квадрат так, чтобы он касался окружности в 4-х точках (рисунок 3,б), то есть сторона квадрата равна диаметру окружности.

Но на рисунке видно, что периметр квадрата явно больше длины вписанной окружности. А что, если внутри окружности построить еще один квадрат? Тогда, возможно, длина окружности будет средней величиной между периметрами двух квадратов.

Измерим длины сторон квадратов с помощью линейки (рисунок 3,в). Длина стороны внутреннего квадрата равна 35 мм, наружного — 50 мм.

Найдем периметры квадратов:

Периметр внутреннего квадрата Р _внутр = 35+35+35+35 = 435= 140 (мм);

Периметр внешнего квадрата Р _внешн = 50+50+50+50= 450 = 200 (мм).

Предположим, что длина окружности — это средняя величина двух периметров. Найдём, чему она равна: (140+200):2 = 170 (мм).

Это значение намного отличается от длины окружности, полученной при измерении с помощью нити — 158 мм, что говорит о невысокой точности этого метода.

Нахождение длины окружности с помощью многоугольников

Далее я предположил, что если внутри окружности построить многоугольник с большим количеством сторон, то его периметр будет больше приближен к длине описанной окружности.

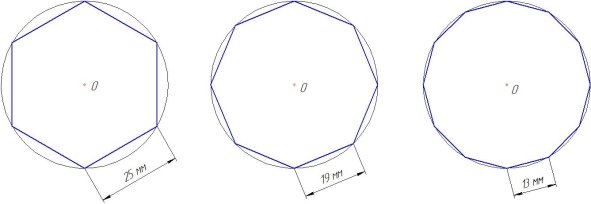
Для того чтобы подтвердить своё предположение, я решил исследовать несколько геометрических фигур: шестиугольник, восьмиугольник, двенадцатиугольник. Диаметр окружности — 50 мм (рисунок 4).

Измерим линейкой длины сторон и с помощью калькулятора найдем периметры построенных фигур.

Периметр шестиугольника (обозначим его Р ₆ ) равен:

Р ₆ = 25+25+25+25+25+25= 625 = 150 (мм).

Найдем периметры восьмиугольника Р ₈ и двенадцатиугольника Р ₁₂ :

Р ₈ = 19+19+19+19+19+19+19+19 = 819 = 152 (мм);

Р ₁₂ = 13+13+13+13+13+13+13+13+13+13+13+13 = 1213 = 156 (мм).

Из полученных результатов можно сделать вывод, что чем больше сторон имеет многоугольник, тем больше его периметр будет приближен к реальной длине окружности, в которую он вписан.

Получение формулы длины окружности экспериментальным методом

От геометрических построений переходим к практическому исследованию и попробуем ответить на вопрос: существует ли связь между диаметром окружности и его длиной.

Экспериментальным способом найдём длины 3-х окружностей диаметром 50, 100 и 200 мм.

Для эксперимента нам понадобятся: 3 металлических круга диаметром 50, 100 и 200 мм, простой карандаш, цветные карандаши, лист ватмана, линейка, рулетка, корпус шариковой ручки, выполняющий роль оси вращения (рисунок 5).

Рис. 5. Подготовка к эксперименту

Для нахождения длины окружности мы будем катить металлический круг, как колесо, по прямой линии, проведенной на листе ватмана. На круге сделана насечка для того, чтобы можно было отметить, когда круг сделает полный оборот. Расстояние, которое пройдет круг за один оборот, и будет являться длиной окружности соответствующего диаметра (рисунок 6).

Рис. 6. Проведение эксперимента

В ходе эксперимента мы получили следующие результаты (рисунок 7).

Длина окружности, диаметр которой D ₁ = 50мм, равна 157мм, то есть L ₁ =157 мм.

Длина окружности диаметром D ₂ =100 мм равна L ₂ =314 мм.

Длина окружности диаметром D ₃ =200 мм равна L ₃ =628 мм.

Рис. 7. Результаты эксперимента

Представим полученные результаты в виде таблицы.

Видео:5 класс, 22 урок, Окружность и кругСкачать

Определите длину окружности монеты: 1) прокатив её по линейке» (рис. 17, а); 2) измерив диаметр монеты (рис. 17, б) и умножив его на число пи — 3,14. Сравните результаты измерений. В каком случае в проводили прямое измерение, в каком — косвенное

Видео:7 класс, 21 урок, ОкружностьСкачать

Ответы 2

В выбранном мною высказывании автор выделяет проблему зависимости поведения и характера действий людей от их потребностей. Каждый человек находится под властью своих безграничных потребностей. Удовлетворяя одни потребности, у него появляются другие, и так по кругу.

Автор высказывания, советский психолог Б.Ф.Ломов, полагает, что «Потребности людей диктуют их поведение с такой же властностью, как сила тяготения — движения физических тел». С этим высказыванием невозможно не согласиться, ведь потребности каждого человека — индивидуальны и если один человек ограничивается удовлетворением биологических потребностей, то другой будет действовать абсолютно по иному, удовлетворяя огромный спектр своих потребностей. Следовательно, если одному будет достаточно чувствовать себя защищенным, быть сытым и не чувствовать жажду, то другой человек хочет общаться, развиваться, ходить в театры — и тоже будет счастлив.

Наши эксперты могут проверить Ваше сочинение по критериям ЕГЭ

ОТПРАВИТЬ НА ПРОВЕРКУ

Эксперты сайта Критика24.ру

Учителя ведущих школ и действующие эксперты Министерства просвещения Российской Федерации.

Как стать экспертом?

Перейдем к теоретическим обоснованиям. Потребность — нужда или недостаток в чем-либо необходимом для поддержания жизнедеятельности организма. Потребности бывают биологическими, социальными, духовными. По А.Маслоу потребности делятся на первичные (физиологические, экзистенциальные) и вторичные (социальные, престижные, духовные). Именно мотивы деятельности человека связаны с удовлетворение его потребностей.

Видео:Длина окружности и площадь кругаСкачать