Параллельные прямые в окружности отсекают равные хорды

Докажем ряд теорем, устанавливающих зависимость между хордами и их дугами в одной и той же окружности или в равных окружностях.

При этом будем иметь в виду дуги, меньшие полуокружности.

Теорема 1. Равные дуги стягиваются равными хордами.

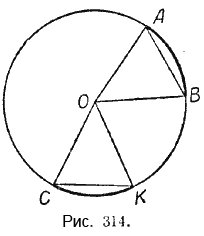
Пусть дуга АВ равна дуге СК. Требуется доказать, что и хорда АВ равна хорде СК (рис. 314).

Доказательство. Соединим концы хорд с центром окружности — точкой О. Полученные треугольники АОВ и КОС равны, так как имеют по две соответственно равные стороны (радиусы одной окружности) и по равному углу, заключённому между этими сторонами (эти углы равны, как центральные, соответствующие равным дугам). Следовательно, АВ = СК.

Теорема 2 (обратная). Равные хорды стягивают равные дуги.

Пусть хорда АВ равна хорде СК. Требуется доказать, что дуга АВ равна дуге СК (рис. 314).

Доказательство. Соединим концы хорд с центром окружности — точкой О. Полученные треугольники АОВ и КОС равны по трём соответственно равным сторонам. Следовательно, равны углы АОВ и СОК; но углы эти центральные, соответствующие дугам АВ и СК; из равенства этих углов следует равенство дуг: (breve = breve).

Теорема 3. Большая дуга стягивается и большей хордой.

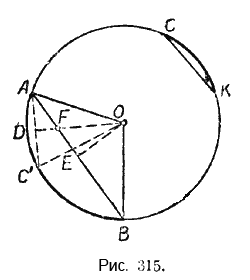
Пусть дуга АВ больше дуги СК (рис. 315).

Требуется доказать, что хорда АВ больше хорды СК.

Доказательство. Передвинем по окружности дугу СК так, чтобы точка К совместилась с точкой А, тогда точка С займёт положение С’ на дуге АВ между точками Aи В, дуга СК примет положение дуги АС’, а хорда СК примет положение хорды АС’. Проведём радиусы в точки A, В и С’. Опустим из центра О перпендикуляры ОЕ и ОD на хорды АВ и АС’. В треугольнике ОFE отрезок ОЕ — катет, а отрезок ОF — гипотенуза, поэтому OF > ОЕ, а потому и OD > OE.

Рассмотрим теперь треугольники ОАD и ОАЕ. В этих треугольниках гипотенуза ОА общая, а катет ОЕ меньше катета ОD, тогда по следствию из теоремы Пифагора катет АЕ больше катета АD. Но эти катеты составляют половины хорд АВ и АС’, значит, и хорда АВ больше хорды АС’. Вследствие равенства хорд АС’ и СК получаем
АВ > СК.

Теорема 4 (обратная). Большая хорда стягивает и большую дугу.

Пусть хорда А В больше хорды СК.

Требуется доказать, что дуга АВ больше дуги СК (рис. 315). Между дугами АВ и СК может существовать только одно из трёх следующих соотношений:

Но дуга AВ не может быть меньше дуги СК, так как тогда по прямой теореме хорда АВ была бы меньше хорды СК, а это противоречит условию теоремы.

Дуга АВ не может быть равна дуге СК, так как тогда хорда АВ равнялась бы хорде СК, а это тоже противоречит условию. Следовательно, (breve > breve).

Свойство дуг, заключенных между параллельными хордами

Теорема. Дуги, заключённые между параллельными хордами, равны.

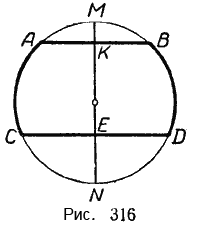
Пусть хорда AB параллельна хорде СD (рис. 316).

Требуется доказать, что (breve = breve). Проведём диаметр MN ⊥ AB. Так как CD || AB, то MN ⊥ CD.
Перегнём чертёж по диаметру MN так, чтобы правая часть совпала с левой.

Тогда точка В совпадёт с точкой А, так как они симметричны относительно оси MN (AB ⊥ MN по построению и AK = KB).

Аналогично, точка D совпадёт с точкой С. Отсюда (breve = breve).

Свойство дуг, заключённых между касательной и параллельной ей хордой

Теорема. Дуги, заключённые между касательной и параллельной ей хордой, равны.

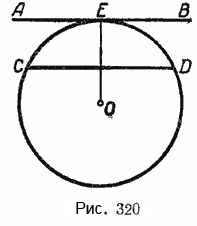
Пусть касательная АВ и хорда СD параллельны. Точка Е — точка касания прямой АВ с окружностью О (рис. 320).

Требуется доказать, что (breve = breve).

Для доказательства соединим точку касания Е с центром круга.

OE ⊥ AB, а так как СD || АВ, то OE ⊥ CD, а перпендикуляр к хорде, проведённый из центра той же окружности, делит стягиваемую ею дугу пополам.

Следовательно, (breve = breve).

Диаметр, перпендикулярный к хорде

Теорема 1. Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею дуги пополам.

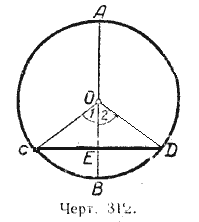
Пусть диаметр AB перпендикулярен к хорде CD (черт. 312). Требуется доказать, что
$$ CE = ED, breve = breve, breve = breve $$

Соединим точки С и D с центром окружности О. В равнобедренном треугольнике СОD отрезок ЕО является высотой, проведённой из вершины О на основание CD; следовательно, ОЕ является и медианой и биссектрисой, т. е. СЕ = ЕD и ∠1 = ∠2. Но ∠1 и ∠2 суть центральные углы. Отсюда равны и соответствующие им дуги, а именно
$$ breve = breve $$
Дуги CA и ВА также равны между собой, как дополняющие равные дуги до полуокружности.

Теорема 2 (обрaтная). Диаметр, проведённый через середину хорды, не проходящей через центр, перпендикулярен к ней и делит дуги, стягиваемые хордой, пополам.

Пусть диаметр AB делит хорду CD пополам. Требуется доказать, что AB ⊥ CD,

Соединим точки С и В с центром круга. Получим равнобедренный треугольник СОD, в котором ОК является медианой, а значит, и высотой. Следовательно, AB⊥CD, а отсюда (по теореме 1) следует, что
$$ breve = breve; breve = breve $$

Теорема 3 (обратная). Диаметр, проведённый через середину дуги, делит пополам хорду, стягивающую эту дугу, и перпендикулярен к этой хорде.

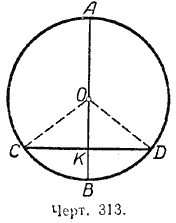
Пусть диаметр AB делит дугу СВD пополам (черт. 313). Требуется доказать, что

Соединим центр круга О с точками С и D. В равнобедренном треугольнике СОD отрезок ОК является биссектрисой угла СОD, так как по условию теоремы (breve) = (breve), поэтому ОК будет и медианой и высотой этого треугольника. Следовательно, диаметр AB проходит через середину хорды и перпендикулярен к ней.

Отрезки и прямые, связанные с окружностью. Теорема о бабочке

Отрезки и прямые, связанные с окружностью

Свойства хорд и дуг окружности

Теоремы о длинах хорд, касательных и секущих

Доказательства теорем о длинах хорд, касательных и секущих

Теорема о бабочке

Отрезки и прямые, связанные с окружностью

Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности

Конечная часть плоскости, ограниченная окружностью

Отрезок, соединяющий центр окружности с любой точкой окружности

Отрезок, соединяющий две любые точки окружности

Хорда, проходящая через центр окружности.

Диаметр является самой длинной хордой окружности

Прямая, имеющая с окружностью только одну общую точку.

Касательная перпендикулярна к радиусу окружности, проведённому в точку касания

Прямая, пересекающая окружность в двух точках

Фигура	Рисунок	Определение и свойства
Окружность
Круг
Радиус
Хорда
Диаметр
Касательная
Секущая

Окружность

Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности

Круг

Конечная часть плоскости, ограниченная окружностью

Радиус

Отрезок, соединяющий центр окружности с любой точкой окружности

Хорда

Отрезок, соединяющий две любые точки окружности

Диаметр

Хорда, проходящая через центр окружности.

Диаметр является самой длинной хордой окружности

Касательная

Прямая, имеющая с окружностью только одну общую точку.

Касательная перпендикулярна к радиусу окружности, проведённому в точку касания

Секущая

Прямая, пересекающая окружность в двух точках

Свойства хорд и дуг окружности

Фигура	Рисунок	Свойство
Диаметр, перпендикулярный к хорде		Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам.
Диаметр, проходящий через середину хорды		Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам.
Равные хорды		Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности.
Хорды, равноудалённые от центра окружности		Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны.
Две хорды разной длины		Большая из двух хорд расположена ближе к центру окружности.
Равные дуги		У равных дуг равны и хорды.
Параллельные хорды		Дуги, заключённые между параллельными хордами, равны.

Диаметр, перпендикулярный к хорде

Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам.

Диаметр, проходящий через середину хорды

Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам.

Равные хорды

Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности.

Хорды, равноудалённые от центра окружности

Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны.

Две хорды разной длины

Большая из двух хорд расположена ближе к центру окружности.

Равные дуги

У равных дуг равны и хорды.

Параллельные хорды

Дуги, заключённые между параллельными хордами, равны.

Теоремы о длинах хорд, касательных и секущих

Произведения длин отрезков, на которые разбита каждая из хорд, равны:

Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.

Фигура	Рисунок	Теорема
Пересекающиеся хорды
Касательные, проведённые к окружности из одной точки
Касательная и секущая, проведённые к окружности из одной точки
Секущие, проведённые из одной точки вне круга

Произведения длин отрезков, на которые разбита каждая из хорд, равны:

Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.

Пересекающиеся хорды

Касательные, проведённые к окружности из одной точки

Касательная и секущая, проведённые к окружности из одной точки

Секущие, проведённые из одной точки вне круга

Пересекающиеся хорды

Произведения длин отрезков, на которые разбита каждая из хорд, равны:

Касательные, проведённые к окружности из одной точки

Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.

Касательная и секущая, проведённые к окружности из одной точки

Секущие, проведённые из одной точки вне круга

Доказательства теорем о длинах хорд, касательных и секущих

Теорема 1 . Предположим, что хорды окружности AB и CD пересекаются в точке E (рис.1).

Тогда справедливо равенство

Доказательство . Заметим, что углы BCD и BAD равны как вписанные углы, опирающиеся на одну и ту же дугу. Углы BEC и AED равны как вертикальные. Поэтому треугольники BEC и AED подобны. Следовательно, справедливо равенство

откуда и вытекает требуемое утверждение.

Теорема 2 . Предположим, что из точки A , лежащей вне круга, к окружности проведены касательная AB и секущая AD (рис.2).

Точка B – точка касания с окружностью, точка C – вторая точка пересечения прямой AD с окружностью. Тогда справедливо равенство

Доказательство . Заметим, что угол ABC образован касательной AB и хордой BC , проходящей через точку касания B . Поэтому величина угла ABC равна половине угловой величины дуги BC . Поскольку угол BDC является вписанным углом, то величина угла BDC также равна половине угловой величины дуги BC . Следовательно, треугольники ABC и ABD подобны (угол A является общим, углы ABC и BDA равны). Поэтому справедливо равенство

откуда и вытекает требуемое утверждение.

Теорема 3 . Предположим, что из точки A , лежащей вне круга, к окружности проведены секущие AD и AF (рис.3).

Точки C и E – вторые точки пересечения секущих с окружностью. Тогда справедливо равенство

Доказательство . Проведём из точки A касательную AB к окружности (рис. 4).

Точка B – точка касания. В силу теоремы 2 справедливы равенства

откуда и вытекает требуемое утверждение.

Теорема о бабочке

Теорема о бабочке . Через середину G хорды EF некоторой окружности проведены две произвольные хорды AB и CD этой окружности. Точки K и L – точки пересечения хорд AC и BD с хордой EF соответственно (рис.5). Тогда отрезки GK и GL равны.

Доказательство . Существует много доказательств этой теоремы. Изложим доказательство, основанное на теореме синусов, которое, на наш взгляд, является наиболее наглядным. Для этого заметим сначала, что вписанные углы A и D равны, поскольку опираются на одну и ту же дугу. По той же причине равны и вписанные углы C и B . Теперь введём следующие обозначения:

Воспользовавшись теоремой синусов, применённой к треугольнику CKG , получим

Воспользовавшись теоремой синусов, применённой к треугольнику AKG , получим

Воспользовавшись теоремой 1, получим

Воспользовавшись равенствами (1) и (2), получим

Проводя совершенно аналогичные рассуждения для треугольников BGL и DGL , получим равенство

откуда вытекает равенство

что и завершает доказательство теоремы о бабочке.

math4school.ru

Окружность

Основные определения

Окружностью называется замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра окружности), которая лежит в той же плоскости, что и кривая.

Отрезок R , который соединяет центр окружности с любой её точкой (а также длина этого отрезка), называется радиусом.

Отрезок DE , который соединяет какие-либо две точки окружности, называется хордой.

Хорда BC , проходящая через центр окружности, называется диаметром.

Диаметр – наибольшая хорда данной окружности. Наименьшей хорды окружности не существует.

Дуга, ∪AB,– это часть окружности, расположенная между двумя её точками.

Вписанным углом, α , называется угол, образованный двумя хордами, имеющими общий конец.

Центральным углом, β , называется угол, образованный двумя радиусами.

Хорды

Параллельные хорды отсекают на окружности равные дуги:

Диаметр, проходящий через середину хорды, перпендикулярен ей:

Хорды окружности равны тогда и только тогда, когда они равноудалены от её центра:

Хорды окружности равны тогда и только тогда, когда они стягивают равные дуги:

Большая из двух хорд окружности расположена ближе к её центру:

Угол, составленный двумя хордами, измеряется полусуммой дуг, заключённых между его сторонами, продолженными в обе стороны:

Если хорды AB и CD пересекаются в точке М, то

Касательные и секущие

Прямая ( a ), которая лежит в одной плоскости с окружностью и имеет с ней только одну общую точку ( B ), называется касательной к этой окружности.

Прямая ( a ), которая перпендикулярна диаметру окружности ( АВ ) и проходит через его конец ( В ), является касательной к этой окружности.

Касательная окружности перпендикулярна диаметру и радиусу, проведённым в точку касания.

Отрезки касательных, проведённые из одной точки, равны:

Углы, образованные касательными, проведёнными из одной точки, и прямой, проходящей через центр окружности и эту точку, равны:

Прямая, которая пересекает окружность в двух различных точках, называется секущей.

Если через точку М вне окружности проведена секущая к ней, то произведение расстояний от точки М до точек пересечения с окружностью равно квадрату длины отрезка касательной, проведённой из точки М к окружности:

Угол, образованный двумя секущими, равен полуразности дуг, заключенных между его сторонами:

Касание двух окружностей

Для двух окружностей с центрами О ₁ и О ₂, и радиусами R и r :

• при внешнем касании: О ₁ О ₂ = R + r ;
• при внутреннем касании: О ₁ О ₂ = R – r .

Углы в окружности

Радиан – угол, который соответствует дуге, длина которой равна радиусу окружности. Один радиан содержит приближённо 57°17’44,8’’.

Радиан принимается за единицу измерения углов при так называемом круговом, или радианном, измерении углов.

Если радианная мера угла равна α , то угол содержит (180· α )/ π градусов.

Если градусная мера угла составляет п ° , то круговая – πп /180 радиан.

Угловой величиной дуги называется величина соответствующего ей центрального угла:

Угловая величина дуги обладает следующими свойствами:

• Угловая величина дуги неотрицательна.
• Равные дуги имеют равные угловые величины.
• Если две дуги одной окружности (или равных окружностей) имеют равные угловые величины, то они равны.

Вписанный угол измеряется половиной дуги, на которую он опирается, и равен половине центрального угла, опирающегося на ту же дугу:

∠ АВС = ½ ·∪ АС = ½ ·∠ АОС .

Вписанные углы, опирающиеся на одну и ту же дугу, равны:

Вписанный угол, опирающийся на полуокружность (диаметр), является прямым:

∠ ACВ = ½ ·∪ АВ = ½ ·180°=90°.

Длина окружности и дуги

Длиной окружности называется общая граница периметров вписанных и описанных правильных многоугольников при неограниченном увеличении числа их сторон.

Отношение длины окружности к длине её диаметра одинаково для всех окружностей и обозначается греческой буквой π .

Длина дуги окружности, выраженной в радианной мере, равна произведению числа её радиан на радиус окружности:

📸 Видео