Вектора, параллельные одной прямой или лежащие на одной прямой называют коллинеарными векторами (рис. 1).
 |
| рис. 1 |
- Условия коллинеарности векторов
- Примеры задач на коллинеарность векторов
- Примеры задач на коллинеарность векторов на плоскости
- Примеры задач на коллинеарность векторов в пространстве
- Условие коллинеарности векторов
- Координатная форма условия коллинеарности векторов
- Доказательства леммы о коллинеарных векторах
- Основные сведения о коллинеарных векторах — свойства координат
- Общие сведения
- Понятие коллинеарности векторов
- Теорема о разложении векторов
- Признаки и свойства коллинеарности векторов
- Примеры задач на коллинеарность векторов на плоскости
- План-график размещения заказов на поставки товаров, выполнение работ, оказание услуг для нужд заказчиков
- Условие коллинеарности векторов
- Координатная форма условия коллинеарности векторов
- 📸 Видео
Видео:89. Разложение вектора по двум неколлинеарным векторамСкачать

Условия коллинеарности векторов
Два вектора будут коллинеарны при выполнении любого из этих условий:
Условие коллинеарности векторов 1. Два вектора a и b коллинеарны, если существует число n такое, что
N.B. Условие 2 неприменимо, если один из компонентов вектора равен нулю.
N.B. Условие 3 применимо только для трехмерных (пространственных) задач.
Доказательство третего условия коллинеарности
Пусть есть два коллинеарные вектора a = < ax ; ay ; az > и b = < nax ; nay ; naz >. Найдем их векторное произведение
Видео:Геометрия 9 класс (Урок№7 - Разложение вектора по двум неколлинеарным векторам. Координаты вектора.)Скачать

Примеры задач на коллинеарность векторов
Примеры задач на коллинеарность векторов на плоскости
Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности, которое в случае плоской задачи для векторов a и b примет вид:
| ax | = | ay | . |
| bx | by |
| Вектора a и b коллинеарны т.к. | 1 | = | 2 | . |
| 4 | 8 |
| Вектора a и с не коллинеарны т.к. | 1 | ≠ | 2 | . |
| 5 | 9 |
| Вектора с и b не коллинеарны т.к. | 5 | ≠ | 9 | . |
| 4 | 8 |
Решение: Так как вектора содержат компоненты равные нулю, то воспользуемся первым условием коллинеарности, найдем существует ли такое число n при котором:
Для этого найдем ненулевой компонент вектора a в данном случае это ay . Если вектора колинеарны то
| n = | by | = | 6 | = 2 |
| ay | 3 |
Найдем значение n a :
Так как b = n a , то вектора a и b коллинеарны.
Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности
| ax | = | ay | . |
| bx | by |
| 3 | = | 2 | . |
| 9 | n |
Решим это уравнение:
| n = | 2 · 9 | = 6 |
| 3 |
Ответ: вектора a и b коллинеарны при n = 6.
Примеры задач на коллинеарность векторов в пространстве
Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности, которое в случае пространственной задачи для векторов a и b примет вид:
| ax | = | ay | = | az | . |
| bx | by | bz |
Вектора a и b коллинеарны т.к. 1 4 = 2 8 = 3 12
Вектора a и с не коллинеарны т.к. 1 5 = 2 10 ≠ 3 12
Вектора с и b не коллинеарны т.к. 5 4 = 10 8 ≠ 12 12
Решение: Так как вектора содержат компоненты равные нулю, то воспользуемся первым условием коллинеарности, найдем существует ли такое число n при котором:
Для этого найдем ненулевой компонент вектора a в данном случае это ay . Если вектора колинеарны то
| n = | by | = | 6 | = 2 |
| ay | 3 |
Найдем значение n a :
Так как b = n a , то вектора a и b коллинеарны.
Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности
| ax | = | ay | = | az | . |
| bx | by | bz |
| 3 | = | 2 | = | m |
| 9 | n | 12 |
Из этого соотношения получим два уравнения:
| 3 | = | 2 |
| 9 | n |
| 3 | = | m |
| 9 | 12 |
Решим эти уравнения:
| n = | 2 · 9 | = 6 |
| 3 |
| m = | 3 · 12 | = 4 |
| 9 |
Ответ: вектора a и b коллинеарны при n = 6 и m = 4.
Видео:9 класс, 1 урок, Разложение вектора по двум неколлинеарным векторамСкачать

Условие коллинеарности векторов
В статье ниже рассмотрим условия, при которых векторы считаются коллинеарными, а также разберем тему на конкретных примерах. И, прежде чем приступить к обсуждению, напомним некоторые определения.
Коллинеарные векторы – ненулевые векторы, лежащие на одной прямой или на параллельных прямых. Нулевой вектор считается коллинеарным любому другому.
Данное определение дает возможность убедиться в коллинеарности векторов в их геометрическом отображении, однако точность такого способа может иметь погрешности, например, в зависимости, от качества самого чертежа. Поэтому обратимся к алгебраическому толкованию: сформируем условие, которое будет явным признаком коллинеарности.
Согласно схемам операций над векторами умножение вектора на некоторое заданное число приводит к соответствующему сжатию или растяжению вектора при сохранении или смене направления. Тогда вектор b → = λ · a → коллинеарен вектору a → , где λ – некоторое действительное число. Справедливым будет и обратное утверждение: если вектор b → коллинеарен вектору a → , его можно представить в виде λ · a → . Это является необходимым и достаточным условием коллинеарности двух ненулевых векторов.
Для коллинеарности двух векторов необходимо и достаточно, чтобы они были связаны равенствами: b → = λ · a → или a → = μ · b → , μ ∈ R
Видео:Вектор. Определение. Коллинеарные векторы. Равные векторы.Скачать

Координатная форма условия коллинеарности векторов
Исходные данные: вектор a → задан в некоторой прямоугольной системе координат на плоскости и имеет координаты ( a x , a y ) , тогда, согласно полученному выше условию, вектор b → = λ · a → имеет координаты ( λ · a x , λ · a y ) .
По аналогии: если вектор a → задан в трехмерном пространстве, то он будет представлен в виде координат a = ( a x , a y , a z ) , а вектор b → = λ · a → имеет координаты ( λ · a x , λ · a y , λ · a z ) . Из полученных утверждений следуют условия коллинеарности двух векторов в координатном толковании.
- Для коллинеарности двух ненулевых векторов на плоскости необходимо и достаточно, чтобы их координаты были связаны соотношениями: b x = λ · a x b y = λ · a y или a x = μ · b x a y = μ · b y
- Для коллинеарности двух ненулевых векторов в пространстве необходимо и достаточно, чтобы их координаты были связаны соотношениями: b x = λ · a x b y = λ · a y b z = λ · a z или a x = μ · b x a y = μ · b y a z = μ · b z
Мы можем также получить еще одно условие коллинеарности векторов, опираясь на понятие их произведения.
Если ненулевые векторы a → = ( a x , a y , a z ) и b → = ( b x , b y , b z ) коллинеарны, то согласно векторному определению произведения a → × b → = 0 → . И это также соответствует равенству: i → j → k → a x a y a z b x b y b z = 0 → , что, в свою очередь, возможно только тогда, когда заданные векторы связаны соотношениями b → = λ · a → и a → = μ · b → , где μ — произвольное действительное число (на основании теоремы о ранге матрицы), что указывает на факт коллинеарности векторов.
Два ненулевых вектора коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору.
Рассмотрим применение условия коллинеарности на конкретных примерах.
Исходные данные: векторы a → = ( 3 — 2 2 , 1 ) и b → = ( 1 2 + 1 , 2 + 1 ) . Необходимо определить, коллинеарны ли они.
Решение
Выполним задачу, опираясь на условие коллинеарности векторов на плоскости в координатах: b x = λ · a x b y = λ · a y Подставив заданные значения координат, получим: b x = λ · a x ⇔ 1 2 + 1 = λ · ( 3 — 2 2 ) ⇒ λ = 1 ( 2 + 1 ) · ( 3 — 2 2 ) = 1 3 2 — 4 + 3 — 2 2 = 1 2 — 1 b y = λ · a y ⇔ 2 + 1 = 1 2 — 1 · 1 ⇔ ( 2 + 1 ) · ( 2 — 1 ) = 1 ⇔ 1 ≡ 1
Т.е. b → = 1 2 — 1 · a → , следовательно, заданные векторы коллинеарны.
Ответ: заданные векторы коллинеарны.
Исходные данные: векторы a → = ( 1 , 0 , — 2 ) и b → = ( — 3 , 0 , 6 ) . Необходимо убедиться в их коллинеарности.
Решение
Т.к. b x = λ · a x b y = λ · a y b z = λ · a z ⇔ — 3 = — 3 · 1 0 = — 3 · 0 6 = — 3 · ( — 2 ) , то верным будет равенство: b → = — 3 · a → , что является необходимым и достаточным условием коллинеарности. Таким образом, заданные векторы коллинеарны.
Найдем также векторное произведение заданных векторов и убедимся, что оно равно нулевому вектору: a → × b → = i → j → k → a x a y a z b x b y b z = i → j → k → 1 0 — 2 — 3 0 6 = i → · 0 · 6 + j → · ( — 2 ) · ( — 3 ) + k → · 1 · 0 — k → · 0 · ( — 3 ) — j → · 1 · 6 — i → · ( — 2 ) · 0 = 0 → Ответ: заданные векторы коллинеарны.
Исходные данные: векторы a → = ( 2 , 7 ) и b → = ( p , 3 ) . Необходимо определить, при каком значении p заданные векторы будут коллинеарны.
Решение
Согласно выведенному выше условию, векторы коллинеарны, если
b → = λ · a → ⇔ b x = λ · a x b y = λ · a y ⇔ p = λ · 2 3 = λ · 7
тогда λ = 3 7 , а p = λ · 2 ⇔ p = 6 7 .
Ответ: при p = 6 7 заданные векторы коллинеарны.
Также распространены задачи на нахождения вектора, коллинеарного заданному. Решаются они без затруднений, основываясь на условии коллинеарности: : достаточным будет взять произвольное действительное число λ и определить вектор, коллинеарный данному.
Исходные данные: вектор a → = ( 2 , — 6 ) . Необходимо найти любой ненулевой вектор, коллинеарный заданному.
Решение
Ответом может послужить, например, 1 2 · a → = ( 1 , — 3 ) или вектор 3 · a → = ( 6 , — 18 ) .
Ответ: вектор, коллинеарный заданному имеет координаты ( 1 , — 3 ) .
Исходные данные: вектор a → = ( 3 , 4 , — 5 ) . Необходимо определить координаты вектора единичной длины, коллинеарного заданному.
Решение
Вычислим длину заданного вектора по его координатам: a → = a x 2 + b x 2 + c x 2 = 3 2 + 4 2 + ( — 5 ) 2 = 5 2 Разделим каждую из заданных координат на полученную длину и получим единичный вектор, коллинеарный данному: 1 a → · a → = ( 3 5 2 , 4 5 2 , — 1 2 )
Видео:Разложение вектора по двум неколлинеарным векторам - 1 часть. Геометрия 9Скачать

Доказательства леммы о коллинеарных векторах
Видео:Коллинеарность векторовСкачать

Основные сведения о коллинеарных векторах — свойства координат
Видео:Разложение вектора по базису. 9 класс.Скачать

Общие сведения
Изучать векторную алгебру начинают на уроках геометрии в средней школе (7 – 9 классы).
Вектор — это отрезок заданной длины и имеющий определенное направление.
С векторами можно выполнять различные математические операции: сложение, вычитание, умножение вектора на число и т. д.
Остановимся на операции умножения вектора на число. Пусть имеется вектор a → , умножим его на некоторое число k. Получим новый вектор b → = k · a → . Векторы a → и b → параллельны и направлены в одну сторону, отличие между ними заключается лишь в длине. Тогда данные векторы можно считать коллинеарными.
Коллинеарностью называется характеристика положения векторов, при котором векторы расположены на одной прямой или на параллельных прямых.
Видео:Разложение вектора по двум неколлинеарным векторам | Геометрия 7-9 класс #85 | ИнфоурокСкачать

Понятие коллинеарности векторов
Из определения следует, что понятие коллинеарный является синонимом понятию параллельный.
Векторы могут быть направлены в одну сторону или же в противоположные. Существует следующее правило для обозначения сонаправленных векторов b → и d → — b → ↑ ↑ d → и противоположно направленных — b → ↑ ↓ d → .
Узнать, являются ли векторы b → ( b 1 ; b 2 ) и d → ( d 1 ; d 2 ) коллинеарными, можно, проверив соблюдение одного из следующих условий:
- b → и d → — пара коллинеарных векторов, если можно найти такое число λ, что b → = λ · d → . Это условие называют леммой о коллинеарности векторов. Докажем ее. Рассмотрим случай, когда b → ↑ ↑ d → . Тогда число λ = b → d → . Векторы являются сонаправленными, так как λ>0. Из условия равенства длин векторов, получим λ · d → = λ · d → = b → d → · d → = b → , что и требовалось доказать. Случай, когда b → ↑ ↓ d → , доказывается аналогично. Возьмем λ = — b → d → , чтобы получить сонаправленные векторы b → и d → . Тогда λ · d → = λ · d → = — b → d → · d → = b → . Лемма доказана. Чтобы понять, являются ли векторы сонаправленными, нужно определить знак λ. Если λ>0, направления векторов совпадают, иначе — не совпадают.
- b → и d → — пара коллинеарных векторов, если соотношения их координат равны между собой: b 1 d 1 = b 2 d 2 . Способ применяется для векторов, среди координат которых нет нулей. Отметим, что данное условие идентично условию параллельности прямых, заданных каноническими уравнениями.
Видео:Разложение вектора по двум неколлинеарным векторам. Урок 4. Геометрия 9 классСкачать

Теорема о разложении векторов
Пусть на плоскости имеются три вектора b → , d → , c → . Тогда, если вектор d → выражается через b → и с → , говорят, что d → можно разложить по b → и c → . При этом вектор d → может быть как коллинеарным с одним из векторов, так и нет.
Сформулируем теорему о разложении векторов.
Любой вектор d → на плоскости можно представить в виде d → = x c → + y b → . При этом c → и b → — пара не коллинеарных векторов, и b → ≠ 0 , c → ≠ 0 . Такое представление называют разложением вектора.
Предположим, что d → коллинеарен b → .
Тогда согласно лемме: d → = y b → . Коэффициент x будет равным нулю, то есть d → = 0 · c → + y b → . Вектор разложен по векторам c → и b → . Теорема доказана.
В пространстве три вектора, два из которых коллинеарны, будут являться компланарными.
Рассмотрим случай, когда среди векторов d → , c → и b → нет коллинеарных.
На плоскости выберем точку M, из которой отложим отрезки M C → = c → , M D → = d → , M B = b → . Из точки D проведем прямую DC1||BM. Вектор d → можно найти по правилу треугольника, то есть d → = М С 1 → + D C 1 → .
D C 1 → и b → — пара коллинеарных векторов, так как лежат на параллельных прямых. Векторы M C 1 → и c → коллинеарны, поскольку лежат на одной прямой. Согласно лемме, D C 1 → = y · b → и M C 1 → = x · c → . Тогда d → = x · c → + y · b → , что и требовалось доказать.
Приведем доказательство, что x и y — однозначно определяемые коэффициенты. Предположим, что существуют x1 и y1, и d → = x 1 · c → + y 1 · b → . Получим, что x · c → + y · b → = x 1 · c → + y 1 · b → , или ( x — x 1 ) · c → + ( y — y 1 ) · b → = 0 .
По условию b → ≠ 0 и c → ≠ 0 , значит, равенство выполнимо только если x — x 1 = 0 и y — y 1 = 0 .
Тогда x = x 1 и y = y 1 , то есть x и y — единственно возможные коэффициенты разложения вектора d → .
Видео:10 класс, 43 урок, Компланарные векторыСкачать

Признаки и свойства коллинеарности векторов
Коллинеарные векторы на плоскости или в пространстве обладают следующими свойствами:
- каждый вектор коллинеарен самому себе b → ↑ ↑ d → ;
- если вектор b → коллинеарен вектору d → , то справедливо обратное утверждение: вектор d → коллинеарен вектору b → ( b → ↑ ↑ d → ⇔ d → ↑ ↑ b → ) ;
- если ненулевой вектор b → коллинеарен ненулевому d → , а d → коллинеарен ненулевому c → , т о b → коллинеарен c → ;
- нулевой вектор коллинеарен любому другому. Нулевым вектор называют вектор, длина которого равна нулю, а начальная и конечная точки совпадают;
- скалярное произведение коллинеарных векторов b → и d → можно вычислить по формулам: b → ↑ ↑ d → ⇒ ( b → · d → ) = b → · d → и b → ↑ ↓ d → ⇒ ( b → · d → ) = — b → · d → .
Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Примеры задач на коллинеарность векторов на плоскости
Определить, являются ли векторы f → ( 4 ; 10 ) и s → ( 2 ; 5 ) коллинеарными.
У векторов нет нулевых координат, проверим соблюдение условия коллинеарности векторов.
Для этого запишем отношения соответствующих координат по форме f 1 s 1 = f 2 s 2 .
Получим: 4 2 = 10 5 .
Ответ: векторы коллинеарные.
Даны три вектора с → ( 1 ; — 2 ) , b → ( 2 , x ) и d → ( 2 ; 2 ) , при этом с → и b → перпендикулярные.
Найти неизвестную координату x. Найти такое число α, при котором b → и d → будут коллинеарными.
Решение. Скалярное произведение перпендикулярных векторов равно нулю. Отсюда найдем неизвестную координату x:
c 1 b 1 + c 2 x = 0 ;
Запишем соотношения координат b → и d → , подставив найденное значение координаты х ( 1 ) :
b 1 d 1 = b 2 d 2 ⇔ 1 2 = 1 2 .
Как видно соотношения координат одинаковы при любом α ∈ R , где R – область действительных чисел.
Ответ: b → и d → коллинеарны при любом α ∈ R .
Дано два вектора d → = 3 , b → = 6 . Найти такое число α, чтобы зависимость вида d → = α b → отображала:
- коллинеарные сонаправленные векторы;
- коллинеарные противоположно направленные векторы.
Решение. Если векторы сонаправлены, то α>0. Получим: 3=6α. Откуда: α=0,5.
Видео:Компланарны ли векторы: a=(2;5;8), b=(1;-3;-7) и c=(0;5;10)?Скачать

План-график размещения заказов на поставки товаров, выполнение работ, оказание услуг для нужд заказчиков
УРОК: «РАЗЛОЖЕНИЕ ВЕКТОРА ПО ДВУМ НЕКОЛЛИНЕАРНЫМ ВЕКТОРАМ»
Тема: Разложение вектора по двум неколлинеарным векторам
Класс: 9 класс
Педагог: , заместитель директора по воспитательной работе, учитель математики и информатики.
Учреждение образования: МОУ Шуринская средняя общеобразовательная школа Кемеровской области
Город: Кемеровская область
Знать формулировку и доказательство леммы о коллинеарных векторах и теорему о разложении по двум неколлинеарным векторам;
Уметь решать задачи, применяя полученные знания.
I. Организационный момент: назвать цели урока.
III. Объяснение нового материала:
1. Разложение вектора по двум неколлинеарным векторам.
При решении задач часто возникает необходимость выразить какой-либо вектор через уже заданные векторы. Такая операция называется разложением вектора по неколлинеарным векторам.
2. Лемма о коллинеарных векторах.
Лемма — это вспомогательное утверждение, с помощью которого доказывается следующая теорема или несколько теорем.
Теорема:Если векторы 




Так как рассматриваемые векторы, по условию коллинеарны, то они могут иметь одинаковые направления. Рассмотрим два случая, когда векторы 


1) 












Видео:РАЗЛОЖЕНИЕ ВЕКТОРА ПО ДВУМ неколлинеарным ВЕКТОРАМ 9 классСкачать

Условие коллинеарности векторов
В статье ниже рассмотрим условия, при которых векторы считаются коллинеарными, а также разберем тему на конкретных примерах. И, прежде чем приступить к обсуждению, напомним некоторые определения.
Коллинеарные векторы – ненулевые векторы, лежащие на одной прямой или на параллельных прямых. Нулевой вектор считается коллинеарным любому другому.
Данное определение дает возможность убедиться в коллинеарности векторов в их геометрическом отображении, однако точность такого способа может иметь погрешности, например, в зависимости, от качества самого чертежа. Поэтому обратимся к алгебраическому толкованию: сформируем условие, которое будет явным признаком коллинеарности.
Согласно схемам операций над векторами умножение вектора на некоторое заданное число приводит к соответствующему сжатию или растяжению вектора при сохранении или смене направления. Тогда вектор b → = λ · a → коллинеарен вектору a → , где λ – некоторое действительное число. Справедливым будет и обратное утверждение: если вектор b → коллинеарен вектору a → , его можно представить в виде λ · a → . Это является необходимым и достаточным условием коллинеарности двух ненулевых векторов.
Для коллинеарности двух векторов необходимо и достаточно, чтобы они были связаны равенствами: b → = λ · a → или a → = μ · b → , μ ∈ R
Видео:Разложение вектора по двум неколлинеарным векторам. Координаты вектораСкачать

Координатная форма условия коллинеарности векторов
Исходные данные: вектор a → задан в некоторой прямоугольной системе координат на плоскости и имеет координаты ( a x , a y ) , тогда, согласно полученному выше условию, вектор b → = λ · a → имеет координаты ( λ · a x , λ · a y ) .
По аналогии: если вектор a → задан в трехмерном пространстве, то он будет представлен в виде координат a = ( a x , a y , a z ) , а вектор b → = λ · a → имеет координаты ( λ · a x , λ · a y , λ · a z ) . Из полученных утверждений следуют условия коллинеарности двух векторов в координатном толковании.
- Для коллинеарности двух ненулевых векторов на плоскости необходимо и достаточно, чтобы их координаты были связаны соотношениями: b x = λ · a x b y = λ · a y или a x = μ · b x a y = μ · b y
- Для коллинеарности двух ненулевых векторов в пространстве необходимо и достаточно, чтобы их координаты были связаны соотношениями: b x = λ · a x b y = λ · a y b z = λ · a z или a x = μ · b x a y = μ · b y a z = μ · b z
Мы можем также получить еще одно условие коллинеарности векторов, опираясь на понятие их произведения.
Если ненулевые векторы a → = ( a x , a y , a z ) и b → = ( b x , b y , b z ) коллинеарны, то согласно векторному определению произведения a → × b → = 0 → . И это также соответствует равенству: i → j → k → a x a y a z b x b y b z = 0 → , что, в свою очередь, возможно только тогда, когда заданные векторы связаны соотношениями b → = λ · a → и a → = μ · b → , где μ — произвольное действительное число (на основании теоремы о ранге матрицы), что указывает на факт коллинеарности векторов.
Два ненулевых вектора коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору.
Рассмотрим применение условия коллинеарности на конкретных примерах.
Исходные данные: векторы a → = ( 3 — 2 2 , 1 ) и b → = ( 1 2 + 1 , 2 + 1 ) . Необходимо определить, коллинеарны ли они.
Решение
Выполним задачу, опираясь на условие коллинеарности векторов на плоскости в координатах: b x = λ · a x b y = λ · a y Подставив заданные значения координат, получим: b x = λ · a x ⇔ 1 2 + 1 = λ · ( 3 — 2 2 ) ⇒ λ = 1 ( 2 + 1 ) · ( 3 — 2 2 ) = 1 3 2 — 4 + 3 — 2 2 = 1 2 — 1 b y = λ · a y ⇔ 2 + 1 = 1 2 — 1 · 1 ⇔ ( 2 + 1 ) · ( 2 — 1 ) = 1 ⇔ 1 ≡ 1
Т.е. b → = 1 2 — 1 · a → , следовательно, заданные векторы коллинеарны.
Ответ: заданные векторы коллинеарны.
Исходные данные: векторы a → = ( 1 , 0 , — 2 ) и b → = ( — 3 , 0 , 6 ) . Необходимо убедиться в их коллинеарности.
Решение
Т.к. b x = λ · a x b y = λ · a y b z = λ · a z ⇔ — 3 = — 3 · 1 0 = — 3 · 0 6 = — 3 · ( — 2 ) , то верным будет равенство: b → = — 3 · a → , что является необходимым и достаточным условием коллинеарности. Таким образом, заданные векторы коллинеарны.
Найдем также векторное произведение заданных векторов и убедимся, что оно равно нулевому вектору: a → × b → = i → j → k → a x a y a z b x b y b z = i → j → k → 1 0 — 2 — 3 0 6 = i → · 0 · 6 + j → · ( — 2 ) · ( — 3 ) + k → · 1 · 0 — k → · 0 · ( — 3 ) — j → · 1 · 6 — i → · ( — 2 ) · 0 = 0 → Ответ: заданные векторы коллинеарны.
Исходные данные: векторы a → = ( 2 , 7 ) и b → = ( p , 3 ) . Необходимо определить, при каком значении p заданные векторы будут коллинеарны.
Решение
Согласно выведенному выше условию, векторы коллинеарны, если
b → = λ · a → ⇔ b x = λ · a x b y = λ · a y ⇔ p = λ · 2 3 = λ · 7
тогда λ = 3 7 , а p = λ · 2 ⇔ p = 6 7 .
Ответ: при p = 6 7 заданные векторы коллинеарны.
Также распространены задачи на нахождения вектора, коллинеарного заданному. Решаются они без затруднений, основываясь на условии коллинеарности: : достаточным будет взять произвольное действительное число λ и определить вектор, коллинеарный данному.
Исходные данные: вектор a → = ( 2 , — 6 ) . Необходимо найти любой ненулевой вектор, коллинеарный заданному.
Решение
Ответом может послужить, например, 1 2 · a → = ( 1 , — 3 ) или вектор 3 · a → = ( 6 , — 18 ) .
Ответ: вектор, коллинеарный заданному имеет координаты ( 1 , — 3 ) .
Исходные данные: вектор a → = ( 3 , 4 , — 5 ) . Необходимо определить координаты вектора единичной длины, коллинеарного заданному.
Решение
Вычислим длину заданного вектора по его координатам: a → = a x 2 + b x 2 + c x 2 = 3 2 + 4 2 + ( — 5 ) 2 = 5 2 Разделим каждую из заданных координат на полученную длину и получим единичный вектор, коллинеарный данному: 1 a → · a → = ( 3 5 2 , 4 5 2 , — 1 2 )
📸 Видео
Разложение вектора по 2 неколлинеарным векторам - bezbotvyСкачать

§15 Коллинеарность векторовСкачать
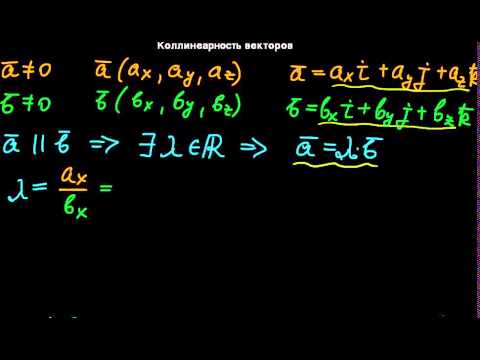
Разложение вектора на неколлинеарные вектора.Скачать

10 класс, 45 урок, Разложение вектора по трем некомпланарным векторамСкачать

Найдите разложение вектора по векторам (базису)Скачать

Геометрия. 9 класс. Разложение любого вектора по двум неколлинеарным векторам /17.09.2020/Скачать




