Сколько различных векторов задают ребра параллелепипеда (4 видео)

Изучение векторов на плоскости и в пространстве

Несмотря на некоторые различия в трактовке понятия вектора в различных учебниках, содержание темы практически не отличается: векторы, равенство векторов, коллинеарность и компланарность векторов, сложение векторов и умножение на число, свойства действий, скалярное произведение и его свойства, разложение вектора на составляющие, координаты векторов, применение векторов к решению задач. При традиционном разделении школьного курса на планиметрию и стереометрию векторы в школе изучаются дважды: в основной школе — векторы на плоскости, а в старшей — векторы в пространстве, при этом часть вопросов (равенство векторов, действия над векторами и их свойства) просто дублируется.

Разрешить данную коллизию можно различными путями. Один из не совсем удачных исходов — исключение этой темы из основной школы (это предполагал не столь давно один из проектов содержания школьного геометрического образования), что вызовет определенные трудности при изучении физики и нарушит целостность геометрических знаний выпускников основной школы. Другой выход — изучение векторов в основной школе в пространстве (на пространственных фигурах). Минимально необходимый набор фактов для успешного изучения физики и применения векторного метода при решении геометрических задач может быть освоен с опорой на знание свойств параллелепипеда. Более глубоко на созданной в основной школе фактологической базе векторы могут быть изучены в старшей школе.

Сделаем ряд замечаний об изучении векторов.

Изучение векторов в курсе геометрии следует согласовать с тем опытом действий над векторами, который приобрели школьники при изучении физики (действия с силами они выполняют уже в 7-м классе).

При рассмотрении вектора следует четко выделить две составляющие: численное значение и направление. Если вектор вводится как направленный отрезок, то следует сразу же рассмотреть равные векторы, для чего необходимо понятие направления. Если же вектор рассматривается как связанный, то необходима операция откладывания вектора.

Основные понятия (вектор, направление, откладывание вектора, нулевой вектор, сонаправленные, противоположно направленные, равные векторы, нулевой вектор, коллинеарные, компланарные векторы) могут быть рассмотрены на одном уроке, сделаны соответствующие выводы, которые могут быть оформлены в виде краткого конспекта. При изучении векторов и координате помощью соответствующих заданий можно существенно активизировать самостоятельную деятельность школьников. Покажем это на серии примеров.

Актуализация имеющегося опыта работы с векторами, рассмотрение основных понятий могут быть организованы в форме обсуждения результатов выполнения следующих заданий.

Из курса физики вы знаете о существовании векторных и скалярных величин. Приведите примеры таких величин. В чем отличия у векторов и скаляров, что общего между ними? Каковы основные характеристики векторных величин? Как изображаются векторы? Что называется вектором? Как связаны с понятием «вектор» такие физические понятия, как «путь», «перемещение», «траектория»?

Выполнив задание 19.1, вы установили, что есть различные определения вектора. Так, вектор определяется как направленный отрезок, как величина, характеризующаяся численным значением и направлением, и даже как параллельный перенос. Удалось ли кому-либо из вас найти иные определения вектора? В каких из названных нами ситуаций направленный отрезок выступает лишь как изображение вектора? При каком условии отрезок превращается в направленный? Как в каждом из случаев определяется нулевой вектор?

Подумайте, почему вектор называют параллельным переносом. Задает ли направленный отрезок параллельный перенос? Задается ли параллельный перенос нулевым вектором?

В Математической энциклопедии в статье «Векторы» написано, что среди векторов выделяют свободные, связанные и скользящие. Как определяются в данной статье названные векторы? Подумайте сами или спросите у учителя физики, чем различаются свободные и связанные векторы?

Рассмотрите модель или изображение параллелепипеда и ответьте на вопросы: сколько различных направлений задают ребра параллелепипеда? Как можно определить понятие «направление»? Какие векторы мы будем называть сонаправленными, противоположно направленными? По рис. 19.1 назовите соиаправлеи- ные, противоположно направленные векторы, Рис. 19.1

начала и концы которых будут точки на ребрах параллелепипеда.

Как вы думаете, какие векторы можно называть равными, противоположными? По рис. 19.1 назовите векторы, задаваемые отмеченными па рисунке точками. Какие из этих векторов будут равны, противоположны?

Как вы думаете, какой вектор можно называть нулевым? Что вы можете сказать о длине и направлении нулевого вектора?

Анализируя термин «коллинеарные векторы», попытайтесь сформулировать определение этого понятия. Как вы думаете, какие векторы будут называться компланарными? Можно ли утверждать, что коллинеарные векторы будут и компланарными? Используя результаты задания 19.5, назовите коллинеарные, компланарные векторы на рис. 19.1.

Можно ли утверждать, что два вектора, сонаправленные третьему, будут сонаправленными? А если эти векторы будут противоположно направлены?

Из курса физики вы знаете, что действие силы на тело зависит от ее численного значения, направления и точки приложения. Какие действия следует выполнить, чтобы отложить вектор, равный данному, от заданной точки? Какие теоретические факты лежат в основе этих действий? Сколько векторов, равных данному, можно отложить от заданной точки? Как вы обоснуете полученный вывод? Какие теоретические факты потребовались для обоснования данного утверждения?

Вспомните определения углов между прямыми, лучами. Какое определение угла между векторами вы можете предложить? Какой будет величина угла между сонаправленными, противоположно направленными векторами?

Выполнение этих заданий позволит ученикам еамоетоятельно получить основной понятийный аппарат темы. Среди выводов, которые будут сделаны в результате выполнения данных заданий, может быть вывод о том, что вектор — класс эквивалентности направленных отрезков, а каждый направленный отрезок есть представитель данного класса (замечание по этому поводу приведено в учебнике «Геометрия 7—9» Л. С. Атанасяна и др.).

Еще раз подчеркнем, что в учебниках А. Д. Александрова, Л. С. Атанасяна, И. М. и В. А. Смирновых операции над векторами вводятся геометрически (по правилу треугольника), а в учебнике А. В. Погорелова — в координатах, хотя исторически векторы складывались по правилу параллелограмма (равнодействующая сил).

Актуализировать опыт учащихся при изучении операций над векторами и организовать их самостоятельную познавательную деятельность поможет выполнение следующих заданий, среди которых имеются и игровые ситуации (задания 19.9, 19.12 и 19.13).

Из курса физики вы знаете, что на тело одновременно могут действовать несколько сил. Какую силу называют равнодействующей этих сил?

Вспомните, как вы в 7-м классе складывали одинаково направленные, противоположно направленные силы. Будет ли двигаться тело под действием двух равных, но противоположно направленных сил?

Какое правило сложения коллинеарных векторов вы можете получить, основываясь на знаниях курса физики?

Один семиклассник, узнав на уроке физики правило сложения со- направленных или противоположно направленных сил, задумался, а как можно сложить силы, не лежащие на одной прямой. Зная, что физические законы выведены опытным путем, он решил провести соответствующий опыт. Дома он взял масштабную модель автомобиля, привязал к ней две прочные нитки и, расположив их под углом друг к другу, потянул за эти нитки. Как двигалась модель автомобиля? Какой была равнодействующая этих сил? Как вы думаете, какое правило сложения двух векторов, отложенных от одной точки, установил ученик в результате данного опыта? А как сложить два вектора, не имеющие общего начала?

Как можно сложить три вектора в пространстве, выходящие из одной точки?

При выполнении предыдущего задания вы установили, что два не- коллинеарных вектора складываются по правилу параллелограмма, выбора точки, от которой отложены векторы? Рис. 19.2

а три — по правилу параллелепипеда. Пользуясь рис. 19.2, сформулируйте правило параллелограмма. Самостоятельно сделайте рисунок, иллюстрирующий правило параллелепипеда.

Можно ли утверждать, что любые два вектора и их сумма будут лежать в одной плоскости?

Зависит ли результат сложения векторов от выбора точки, от которой отложены векторы?

Рассматривая рис. 19.2 и пытаясь найти на нем равные векторы, одна ученица обнаружила, что два вектора можно сложить по правилу треугольника. Сформулируйте это правило.

Учитель предложил на уроке задание на сложение пяти векторов. Ученик спросил у своего соседа по парте, не знает ли он правило сложения нескольких векторов. Тот сказал, что есть правило многоугольника, но не успел объяснить, в чем оно состоит, поскольку его вызвали к доске решать задачу. Попробуйте самостоятельно решить эту задачу. Как вы думаете, в чем состоит правило многоугольника? Как сложить несколько векторов, не лежащих в одной плоскости? Задайте на рис. 19.1 несколько векторов, лежащих на ребрах параллелепипеда, и найдите их сумму.

Вы знаете, что сложение чисел обладает рядом свойств. Что это за свойства? Может ли обладать соответствующими свойствами действие сложения векторов? Ответ на этот вопрос и обоснование ответа вам помогут дать рис. 19.2 и 19.3.

X V/ X л. A vy V» V/ 4 1 1 V/ШЛ! II1V vy 1 1У4 1 хл iywi’1 11 vy —

могут дать рис. 19.2 и 19.3. Рис. 193

В результате выполнения этих заданий должны быть сформулированы правила треугольника и многоугольника, параллелограмма и параллелепипеда, а также свойства сложения векторов.

Другие действия над векторами могут быть введены при выполнении ряда заданий.

Вспомните определение разности двух чисел. Можно ли заменить вычитание чисел сложением? Как можно вычесть из одного вектора другой? Выполняли ли вы вычитание векторов, изучая физику? Можно ли заменить операцию вычитания двух векторов сложением? Какое правило вычитания векторов вы установили, выполняя данное задание?

Нарисуйте вектора. Найдите сумму а +а+а. Каким будет результат. Сравните его характеристики с характеристиками вектора а. Можно ли записать результат, используя символику умножения? Сделайте это. Попробуйте самостоятельно сформулировать определение произведения вектора на число. Как можно построить — вектора а? Как по- 5 3

строить векторы -2а, -а?

Будут ли вектор а и построенные вами векторы коллинеарными? Ответ обоснуйте.

Изучая коллинеарность или компланарность векторов, обоснования необходимых и достаточных условий коллинеарности и компланарности можно предложить ученикам, интересующимся геометрией, для самостоятельного изучения. Организовать самостоятельную работу помогут следующие задания.

Найдите в учебнике или справочнике достаточное условие коллинеарности векторов. Как обосновать это утверждение? Останется ли оно верным, если вектор а будет нулевым? Сформулируйте утверждение, обратное достаточному условию коллинеарности. Какую гипотезу о его истинности вы можете предложить? Получить обоснования данного утверждения вы можете, заполнив пропуски в приведенном ниже тексте.

Итак, даны коллинсарныс векторы а и /;, и нам надо показать, что существует такое число X, что b = Ха [*] (или а = xb [**]).

Во-первых, отметим, что один из векторов или оба могут быть нулевыми. Если а = Ъ = 0, то в качестве коэффициента X можно выбрать . Если b = 0, то равенство [*] будет выполняться при X = .

Если а = 0, то аналогично мы можем получить равенство . Во-вторых, если выполняется равенство [*], то равенство [**] будет справедливо при р = .

Теперь предположим, что оба вектора ненулевые, и обоснуем равенство [*]. Для проверки его истинности нам надо установить, что векторы b и Ха . и их длины .

Проверим второе условие.

Введем число к = и рассмотрим вектор ка. к. 0. ка = . |я| = а

= -j—|-|а| = . Получили, что длины векторов ка и . равны. Итак, если а

X = к, то длины векторов b и Ха .

Если a ft b, то Ха и b будут сонаправлены при X = . Если а || Ь, то Ха и b будут сонаправлены при X = .

Итак, мы установили, что если а || Ь, то X = если а || Ь, то X = .

Сформулируйте результат задачи в терминах необходимости и достаточности. Как вы думаете, будет ли единственным найденный коэффициент? Вспомните, каким способом мы проверяли единственность какого-либо элемента.

Не сможете ли вы сформулировать на векторном языке необходимое и достаточное условие принадлежности точки С прямой АВ? Его часто называют условием принадлежности трех точек одной прямой.

Выполнив задание 19.17 о необходимом и достаточном условии коллинеарности векторов, два ученика задумались об условиях компланарности векторов. В справочнике но математике они нашли следующее утверждение: «Векторы а,Ьис компланарны тогда и только тогда, когда существуют такие числа аир, что выполняется равенство с = аа + рЬ». Они решили доказать прямое и обратное утверждения. Один из них нарисовал параллелограмм и сказал, что доказательство одного из утверждений следует из рисунка. Что это за утверждение? Какие рассуждения выполнил ученик, обосновывая свой вывод? Могли ли быть неточности на рисунке или в обоснованиях? Его товарищ сказал, что обратное к доказанному утверждение вообще очевидно. Как он рассуждал? Учли ли ученики в своих рассуждениях, что какой-либо из векторов может быть нулевым, что среди трех векторов могут быть коллинеарные?

Пользуясь найденным учениками результатом, сформулируйте в векторной форме необходимое и достаточное условие принадлежности точки М плоскости, определяемой тремя точками К, Р, N.

Изучая действия над векторами, важно обратить внимание учеников на аналогии между действиями над числами и действиями над векторами, для учащихся, интересующихся математикой, можно указать, что векторы с введенными действиями образуют специальную структуру — линейное пространство.

Отметим, что при изучении векторов в основной школе недостаточное внимание уделяется разложению вектора на составляющие, что потребуется при вычислении скалярного произведения, при вычислении длин отрезков, вычислении углов, особенно в пространстве, наконец, для введения координат вектора, установления связи между векторным и координатным методами.

Теорему о разложении вектора на составляющие можно «разыграть» как микроисследование школьников, описанное в следующем задании.

Продолжая листать справочник, ученики, решившие задачу 19.18, обнаружили еще одно важное утверждение: «Любой вектор в пространстве можно разложить по трем данным некомпланариым векторам, причем коэффициенты разложения определяются единственным образом». Вспомнив предшествующий опыт разложения вектора на составляющие и решение задачи 19.17, они поняли, что для обоснования возможности равенства р = аа + fib + ус, где/? — произвольный вектор, а а_УЬ,с — данные некомпланарные векторы, следует построить параллелепипед, в котором вектор р задает диагональ, а ребра будут параллельны векторам а,Ьис. Опишите подробно построение. Всегда ли оно возможно? Почему оно приведет к требуемому результату? Выполните обоснования. Каким может быть расположение вектора р относительно я, b и с?

Для доказательства единственности разложения ученики записали несколько равенств. Прокомментируйте эти записи. В чем состоит противоречие с условием? Какими теоретическими фактами воспользовались авторы доказательства?

Если, например, а, — а₂ ^ 0, то

Далее в справочнике ученики прочитали, что если векторы а,Ь и с будут единичными и ортогональными (как вы думаете, что это значит?), то коэффициенты разложения вектора/? по векторам я, b и с будут называться координатами векторар.

Как вы думаете, будет ли следовать из найденной учениками теоремы соответствующее утверждение для векторов, лежащих в плоскости? Сформулируйте это утверждение. Каким будет обоснование?

Изучение темы «Скалярное произведение векторов и его свойства» может быть организовано в виде семинара, на котором обсуждаются результаты выполнения учениками ряда заданий по теме. При выполнении приведенных ниже заданий ученики обращаются к различным учебникам или справочникам но математике.

Семинар может быть построен на основании результатов, полученных школьниками при выполнении задания 19.20, вновь представленного как игровая ситуация.

На уроке по теме «Скалярное произведение векторов и его свойства» учитель сформулировал определение скалярного произведения векторов а и b: аЪ = |a||ft|cosZ(5; Ь), его свойства:

1) й 2 >0;
2)ab =Ьа (переместительный закон);
3) (ka)b = k(ab) (сочетательный закон);
4) (а + Ь)с =ас + Ьс (распределительный закон)

и формулу для вычисления скалярного произведения в координатах ah = х_хх₂ + у_ху₂ + z,z₂ и попросил учеников дома выбрать наиболее заинтересовавшее их утверждение и подготовить его обоснование к следующему уроку в форме рассказа с пропусками.

Один ученик, придя домой и начав подготовку этого задания, понял, что доказательство первого и второго свойств очевидны, как и доказательство третьего для к > 0, а для отрицательного коэффициента углы между векторами а и b и векторами ка и kb окажутся смежными. Восстановите ход рассуждений ученика по поводу доказательства этих свойств.

Продолжая работать над заданием, ученик убедился, что самостоятельно придумать обоснование распределительного закона не так просто, и поэтому именно его и нужно подготовить для рассказа на уроке. Он нашел обоснование этого свойства во взятом у старшего брата-сту- дента учебнике геометрии для вузов А. Д. Александрова и Н. Ю. Нс- цветаева, разобрал его и оформил в виде задания с пропусками следующим образом.

Сначала нужно установить истинность двух формул

при этом вторая формула получается из первой заменой. поэтому докажем формулу (19.1). Отложим векторы от одной точки и получим ОА =а, О В =b, АВ =Ь — а, по теореме косинусов для треугольника ОАВ АВ 2 = ОА 2 + . — 2. ОВ, на векторном языке это равенство принимает вид (а — b) 2 = а 2 + . — 2. |6|cos. Если последнее слагаемое мы заменим . векторов, то получим равенство (19.1). Почленно сложив (19.1) и (19.2), имеем

Введем вспомогательные векторы р = а + /; и q = а + с, применим к ним формулу (19.3). Получаем

Сложив левые и правые части этих двух равенств, получаем

С другой стороны,

Учитывая (19.4), сопоставляем (19.5) и (19.6) и получаем требуемое равенство (а + b)c =ас + he.

Заполните пропуски в данном доказательстве.

Что касается формулы для вычисления скалярного произведения в координатах, сказал себе ученик, то раз в нем участвуют координаты векторов, а они — коэффициенты разложения векторов а и Ь по единичным векторам i,j, k, то для доказательства формулы мы можем перемножить разложения, применив доказанные свойства скалярного произведения.

Реализуйте составленный учеником план вывода формулы для вычисления скалярного произведения в координатах.

Обоснование какого из этих свойств вы бы подготовили для собственного выступления на уроке?

Другой ученик, выполняя это же задание и рассматривая формулы, понял, что все свойства скалярного произведения можно очень просто обосновать, если сначала доказать формулу для вычисления скалярного произведения в координатах. Но как эго сделать, не пользуясь свойствами? Рассматривая формулу

он подумал, что можно попытаться применить теорему косинусов, связывающую длины векторов и косинус угла, а для длины вектора уже была выведена координатная формула без использования свойств скалярного произведения. Сделав рисунок, ученик записал несколько равенств:

Теперь, сказал он, в последнюю формулу нужно подставить выражения для координат, преобразовать, и должна получиться формула скалярного произведения в координатах.

Прав ли ученик в своем предположении? Как были получены написанные им формулы? Можно ли воспользоваться его рассуждением, если векторы окажутся коллинеарными? А как быть в том случае, когда какой-либо из векторов будет нулевым?

Третий ученик, у которого не было времени для выполнения задания, по дороге на тренировку открыл в метро учебник геометрии А. В. Погорслова и увидел, что в этом учебнике скалярное произведение векторов определяется как сумма произведений одноименных координат, из-за чего все свойства скалярного произведения доказываются мгновенно. Но наш учитель, вспомнил ученик, давал другое определение скалярного произведения. И если бы я сумел доказать, что определения равносильны, то домашнее задание было бы перевыполнено (ученик, как вы понимаете, занимался не только спортом, но и геометрией). Читая учебник дальше, он увидел, как из формулы аЪ = х_хх₂ + у_ху₂ + z,z₂ выводится формула ab = = |5||6|cos(Zfl; /;), а обратного вывода нет. Познакомьтесь с этим текстом, поделитесь своими знаниями с одноклассниками. Подумайте, каким может быть обратный вывод.

Важнейшим вопросом при изучении векторов является появление нового метода решения геометрических задач — векторного метода. Суть векторного метода учитель может сформулировать для учащихся следующим образом: геометрические понятия и отношения переводятся на векторный язык, выполняются преобразования на векторном языке на основе законов векторной алгебры, полученные результаты переводятся на геометрический язык и осмысливаются в геометрических понятиях. Примеры перевода представлены в табл. 19.1.

Содержание

Мерзляк 5 класс — § 22. Прямоугольный параллелепипед. Пирамида
Вопросы к параграфу
Решаем устно
Упражнения
Упражнения для повторениях
Задача от мудрой совы
Прямоугольный параллелепипед
📸 Видео

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Мерзляк 5 класс — § 22. Прямоугольный параллелепипед. Пирамида

Вопросы к параграфу

1. Какие предметы дают представление о прямоугольном параллелепипеде?

Коробка, кирпич, спичечный коробок, ящик, пакет молока или сока, платяной шкаф и т.д.

2. Из каких фигур состоит поверхность прямоугольного параллелепипеда?

Из шести прямоугольников.

3. Сколько граней имеет прямоугольный параллелепипед?

4. Сколько пар противолежащих граней имеет прямоугольный параллелепипед?

У прямоугольного параллелепипеда три паны противолежащих граней.

5. Каким свойством обладают противолежащие грани прямоугольного параллелепипеда?

Противолежащие грани прямоугольного параллелепипеда равны.

6. Как называют стороны граней прямоугольного параллелепипеда?

Стороны граней прямоугольного параллелепипеда называют рёбрами.

7. Как называют вершины граней прямоугольного параллелепипеда?

Вершины граней прямоугольного параллелепипеда называют вершинами.

8. Сколько вершин имеет прямоугольный параллелепипед?

Прямоугольный параллелепипед имеет 8 вершин.

9. Сколько рёбер имеет прямоугольный параллелепипед?

Прямоугольный параллелепипед имеет 12 рёбер.

10. Какое общее название имеют длины трёх рёбер прямоугольного параллелепипеда, имеющих общую вершину?

11. Какие названия измерений прямоугольного параллелепипеда используют для их различия?

Длина, ширина, высота.

12. Какую фигуру называют кубом?

Куб — это прямоугольный параллелепипед, у которого все измерения равны.

13. Из каких фигур состоит поверхность куба?

Из шести равных квадратов.

14. Из каких фигур состоит поверхность пирамиды?

Поверхность пирамиды состоит из боковых граней — треугольников, имеющих общую вершину, и основания.

15. Какую пирамиду называют треугольной? Четырёхугольной?

Треугольной пирамидой называют пирамиду, у основания которой три стороны, то есть основание является треугольником.

Четырехугольной пирамидой называют пирамиду, у основания которой четыре стороны, то есть основание является четырёхугольником.

16. Что называют вершиной пирамиды?

Вершиной пирамиды называют общую вершину боковых граней.

17. Что называют рёбрами основания пирамиды?

Стороны основания пирамиды называют рёбрами основания пирамиды.

18. Что называют боковыми рёбрами пирамиды?

Боковыми рёбрами пирамиды называют стороны боковых граней, не принадлежащие основанию.

Решаем устно

1. Вычислите:

13 • 4 • 25 = 13 • (4 • 25) = 13 • 100 = 1 300
4 • 5 • 78 • 5 = (4 • 5) • 78 • 5 = (20 • 5) • 78 = 100 • 78 = 7 800
125 • 943 • 8 = (125 • 8) • 943 = 1 000 • 943 = 943 000

2. Упростите выражение:

3a • 16b = 48 ab
4m •9n •5k = 180 mnk
7a •2b •50c •8d = 5600 abcd

3. Раскройте скобки:

2(a + b) = 2a + 2b
(3 — b) • 5 = 3 • 5 — b • 5 = 15 — 5b
6m(7n + 8p) = 6m • 7n + 6m • 8p = 42 mn + 48 mp

4. Найдите периметр прямоугольника, площадь которого равна 28 см², а одна из его сторон — 7 см.

1) 28 : 7 = 4 (см) — длина второй стороны прямоугольника.

2) (4 + 7) • 2 = 11 • 2 = 22 (см) — периметр прямоугольника.

Ответ: периметр равен 22 см.

5. В магазине разложили 6 ц яблок в ящики так, что в каждом ящике оказалось по 12 кг яблок. Сколько ящиков заполнили яблоками?

600 : 12 = 50 (ящиков) — заполнили яблоками.

Ответ: 50 ящиков.

6. Во сколько раз площадь квадрата, сторона которого равна 6 см, больше площади квадрата со стороной 2 см?

1) 6 • 6 = 36 (см²) — площадь квадрата со стороной 6 см.

2) 2 • 2 = 4 (см²) — площадь квадрата со стороной 2 см.

3) 36 : 2 = 18 (раз) — площадь квадрата со стороной 6 см больше площади квадрата со стороной 2 см.

Упражнения

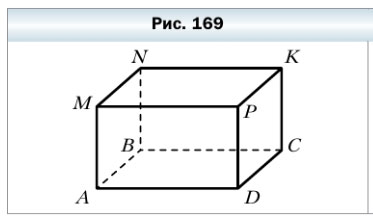
598. На рисунке 169 изображён прямоугольный параллелепипед ABCDMNKP. Назовите:

1) грани, которым принадлежит вершина С — ABCD, NKCB, PKCD

2) рёбра, равные ребру ВС — AD, MP, NK

3) верхнюю грань — MNKP

4) вершины, принадлежащие нижней грани — A, B, C, D

5) грани, имеющие общее ребро AM — AMNB, AMPD

6) грань, равную грани DPKC — AMNB

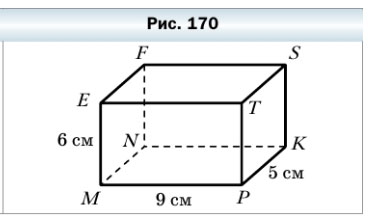
599. Измерения прямоугольного параллелепипеда MNKPEFST (рис. 170) равны 9 см, 5 см и 6 см. Вычислите сумму длин всех его рёбер и площадь его поверхности.

В прямоугольном параллелепипеде MNKPEFST всего 12 рёбер:

рёбро EM = FN = SK = TP = 6 см
рёбро MP = ET = FS = NK = 9 см
рёбро PK = MN = EF = TS = 5 см

6 • 4 + 9 • 4 + 5 • 4 = 24 + 36 + 20 = 80 (см) — длина всех рёбер прямоугольного параллелепипеда MNKPEFST.

Поверхность прямоугольного параллелепипеда состоит из 6 граней:

площадь грани EFST = MNKP = 5 • 9 = 45 см²
площадь грани EFNM = TSKP = 6 • 5 = 30 см²
площадь грани ETPM = FSKN = 9 • 6 = 54 см²

45 • 2 + 30 • 2 + 54 • 2 = 90 + 60 + 108 = 258 (см²) — площадь поверхности прямоугольного параллелепипеда MNKPEFST.

Ответ: длина всех рёбер 80 см, площадь поверхности 258 см².

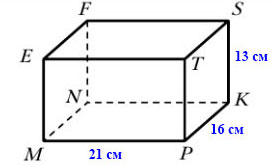
600. Найдите сумму длин всех рёбер прямоугольного параллелепипеда, измерения которого равны 13 см, 16 см, 21 см.

В прямоугольном параллелепипеде MNKPEFST всего 12 рёбер:

рёбро EM = FN = SK = TP = 13 см
рёбро MP = ET = FS = NK = 21 см
рёбро PK = MN = EF = TS = 16 см

13 • 4 + 16 • 4 + 21 • 4 = 52 + 64 + 84 = 200 (см) — длина всех рёбер прямоугольного параллелепипеда MNKPEFST.

Ответ: длина всех рёбер 200 см.

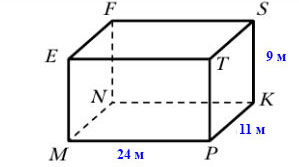
601. Найдите площадь поверхности прямоугольного параллелепипеда, измерения которого равны 9 м, 24 м, 11 м.

Поверхность прямоугольного параллелепипеда состоит из 6 граней:

площадь грани EFST = MNKP = 24 • 11 = 264 м²
площадь грани EFNM = TSKP = 9 • 11 = 99 м²
площадь грани ETPM = FSKN = 24 • 9 = 216 м²

264 • 2 + 99 • 2 + 216 • 2 = 528 + 198 + 432 = 1 158 (м²) — площадь поверхности прямоугольного параллелепипеда MNKPEFST.

Ответ: площадь поверхности 1 158 м².

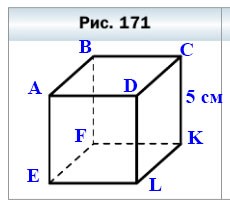
602. Вычислите площадь поверхности и сумму длин всех рёбер куба (рис. 171), ребро которого равно 5 см.

В кубе ABCDEFKL всего 12 рёбер и они все равны 5 см.

5 • 12 = 60 (см) — длина всех рёбер куба ABCDEFKL.

Поверхность куба состоит из 6 граней и они все равны 5 • 5 = 25 см²

25 • 6 = 150 (см²) — площадь поверхности куба ABCDEFKL.

Ответ: длина всех рёбер 60 см, площадь поверхности 150 см².

603. Найдите сумму длин всех рёбер и площадь поверхности куба, если его ребро равно 7 см.

В кубе ABCDEFKL всего 12 рёбер и они все равны 7 см.

7 • 12 = 84 (см) — длина всех рёбер куба ABCDEFKL.

Поверхность куба состоит из 6 граней и они все равны 7 • 7 = 49 см²

49 • 6 = 294 (см²) — площадь поверхности куба ABCDEFKL.

Ответ: длина всех рёбер 84 см, площадь поверхности 294 см².

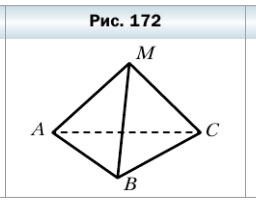
604. На рисунке 172 изображена пирамида МАВС. Укажите:

1) основание пирамиды — ABC

2) вершину пирамиды — M

3) боковые грани пирамиды — AMB, AMC, BMC

4) боковые рёбра пирамиды — AM, BM, CM

5) рёбра основания пирамиды — AB, BC, AC

605. На рисунке 173 изображена пирамида SABCD. Укажите:

1) основание пирамиды — ABCD

2) вершину пирамиды — S

3) боковые грани пирамиды — ADS, DCS, CBS, ABS

4) боковые рёбра пирамиды — AS, BS, CS, DS

5) рёбра основания пирамиды — AB, BC, CD, DA

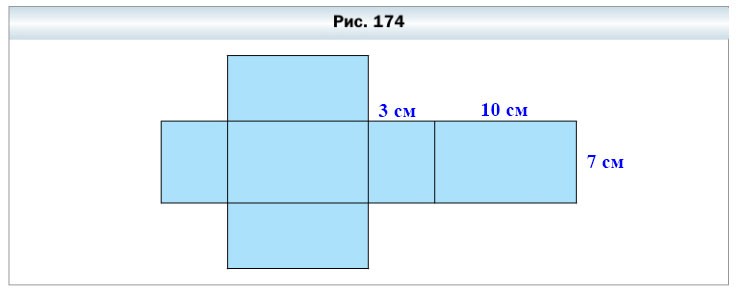
606. На рисунке 174 изображена развёртка прямоугольного параллелепипеда.

1) Из скольких прямоугольников состоит развёртка? — из 6 прямоугольников.

2) Сколько пар равных прямоугольников содержит развёртка? — 3-х пары равных прямоугольников.

3) Какова площадь этой развёртки, если измерения параллелепипеда равны 10 см, 7 см и 3 см?

S = (10 • 7) • 2 + (3 • 10) • 2 + (7 • 3) • 2 = 70 • 2 + 30 • 2 + 21 • 2 = 140 + 60 + 42 = 242 см²

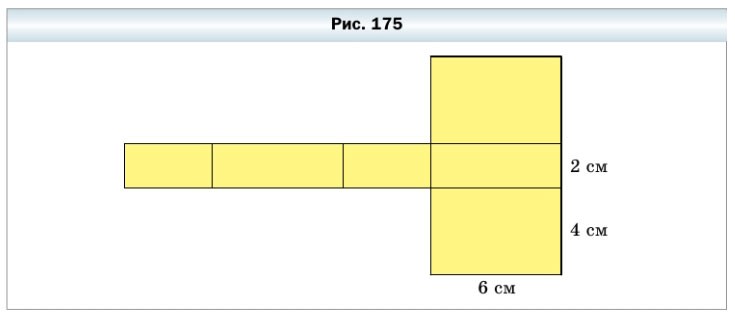
607. Вычислите площадь поверхности прямоугольного параллелепипеда, развёртка которого изображена на рисунке 175.

S = (6 • 4) • 2 + (6 • 2) • 2 + (4 • 2) • 2 = 24 • 2 + 12 • 2 + 8 • 2 = 48 + 24 + 16 = 88 см²

Ответ: площадь поверхности равна 88 см².

608. Высота прямоугольного параллелепипеда равна 20 см, что на 5 см больше его ширины и в 3 раза меньше его длины. Вычислите площадь поверхности параллелепипеда.

1) 20 — 5 = 15 (см) — ширина прямоугольного параллелепипеда.

2) 20 • 3 = 60 (см) — длина прямоугольного параллелепипеда

3) (60 • 20) • 2 + (60 • 15) • 2 + (20 • 15) • 2 = 1 200 • 2 + 900 • 2 + 300 • 2 = 2 400 + 1 800 + 600 = 4 800 (см²) — площадь поверхности прямоугольного параллелепипеда.

Ответ: S = 4 800 см².

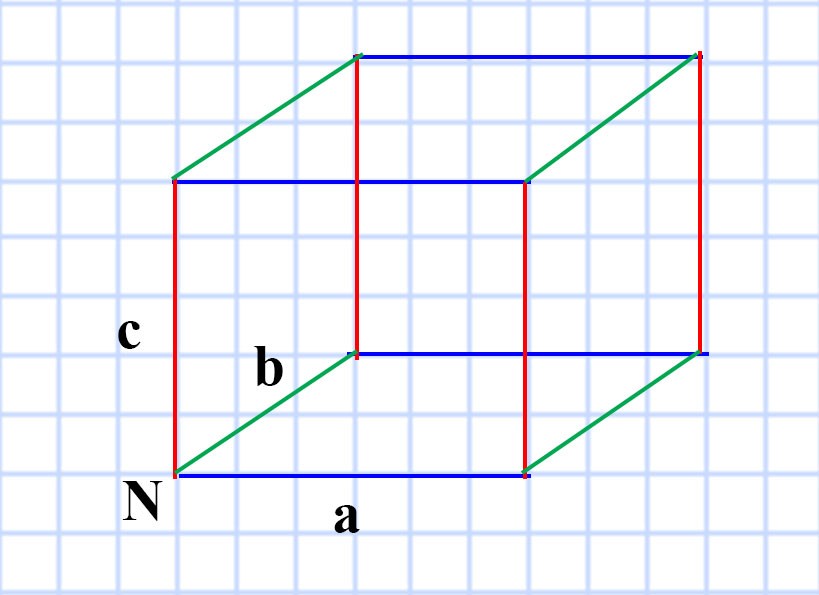
609. Сумма длин всех рёбер прямоугольного параллелепипеда равна 28 см. Найдите сумму длин трёх его рёбер, имеющих общую вершину.

В прямоугольном параллелепипеде всего 12 ребер. Причём:

4 ребра равны длине a — рёбра синего цвета
4 ребра равны ширине b — рёбра зелёного цвета
4 ребра равны ширине c — рёбра красного цвета

Мы знаем, что сумма длин всех рёбер этого прямоугольного параллелепипеда равна 28 см.

Значит, можно записать:

4a + 4b + 4с = 28
4 (a + b + с ) = 28
a + b + с = 28 : 4
a + b + с = 7 (см)

Так как рёбра a, b и с сходятся в общей вершине N, то искомая сумма длин трёх рёбер прямоугольного параллелепипеда, имеющих общую вершину равна 7 см.

610. Прямоугольный параллелепипед и куб имеют равные площади поверхностей. Длина параллелепипеда равна 18 м, что в 2 раза больше, чем его ширина, и на 8 м больше, чем его высота. Найдите ребро куба.

1) 18 : 2 = 9 (м) — ширина параллелепипед.

2) 18 — 8 = 10 (м) — высота параллелепипеда.

3) (18 • 9) • 2 + (18 • 10) • 2 + (10 • 9) • 2 = 162 • 2 + 180 • 2 + 90 • 2 = 324 + 360 + 180 = 864 (м²) — площадь поверхности параллелограмма.

Значит площадь поверхности куба равна 864 м². Так как у куба всего 6 граней и все они одинаковы, то можно найти площадь грани куба.

4) 864 : 6 = 144 (м²) — площадь грани куба.

Для того, чтобы найти длину ребра куба, надо подобрать такое число, квадрат которого будет равняться числу 144. Это число 12 (12 • 12 = 144).

Значит длина ребра куба равна 12 м.

Ответ: 12 метров.

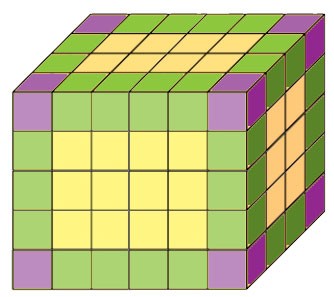
611. Брусок, имеющий форму прямоугольного параллелепипеда с измерениями 4 см, 5 см и 6 см, покрасили со всех сторон и разрезали на кубики с ребром 1 см. Сколько получилось кубиков, у которых:

1) окрашено три грани — 8 кубиков (фиолетовые), которые расположены по вершинам прямоугольного параллелепипеда.

2) окрашено две грани — 36 кубков (зелёные), которые расположены по рёбрам параллелепипеда, но не являются его вершинами (4 • 4 + 3 • 4 + 2 • 4 = 16 + 12 + 8 = 36):

по 4 кубика на 4 рёбрах длиной 6 см
по 3 кубика на 4 рёбрах длиной 5 см
по 2 кубика на 4 рёбрах длиной 4 см

3) окрашено одна грань — 52 кубика (жёлтые), которые не примыкают ни к вершинам, ни к рёбрам параллелепипеда (12 • 2 + 8 • 2 + 6 • 2 = 24 + 16 + 12 = 52):

4 • 3 = 12 кубиков на двух гранях размерами 6 см х 5 см
4 • 2 = 8 кубиков на двух гранях размерами 6 см х 4 см
3 • 2 = 6 кубиков на двух гранях размерами 5 см х 5 см

Упражнения для повторениях

612. Скорость космического корабля «Восток», на котором Юрий Гагарин совершил свой полёт, равна 8 км/с.

1) За сколько минут он пролетал 960 км?

960 : 8 = 120 (с) — нужно кораблю для преодоления 960 км.

2) Какое расстояние он пролетал за 1 ч?

1 ч = 60 мин = 3 600 с

8 • 3 600 = 28 800 (км) — пролетает корабль за 1 час.

Ответ: 28 800 км.

613. Из листа картона можно вырезать шесть одинаковых квадратов. Сколько листов картона надо для того, чтобы вырезать 50 таких квадратов?

Значит нужно 8 + 1 = 9 листов.

614. Поезд отправился со станции в 16 ч со скоростью 54 км/ч. В 19 ч с этой же станции в противоположном направлении отправился второй поезд. В 24 ч расстояние между ними было равно 642 км. С какой скоростью двигался второй поезд?

1) 24 — 16 = 8 (часов) — двигался первый поезд.

2) 54 • 8 = 432 (км) — проехал первый поезд за 8 часов.

3) 24 — 19 = 5 (часов) — двигался второй поезд.

4) 642 — 432 = 210 (км) — проехал второй поезд за 5 часов.

5) 210 : 5 = 42 (км/ч) — скорость второго поезда.

615. Решите уравнение:

Задача от мудрой совы

616. Как с помощью линейки измерить диагональ кирпича, имея ещё несколько таких кирпичей? (Диагональ параллелепипеда — это отрезок, соединяющий две его вершины, не принадлежащие одной грани.)

Для этого нам потребуется как минимум 3 кирпича:

Сложим кирпичи лесенкой
Линейкой измерим расстояние так, как показано на рисунке.
Измеренное расстояние будет точно соответствовать длине диагонали кирпича.

Видео:Выразить векторы. Разложить векторы. Задачи по рисункам. ГеометрияСкачать

Прямоугольный параллелепипед

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

На этом уроке все желающие смогут изучить тему «Прямоугольный параллелепипед». В начале урока мы повторим, что такое произвольный и прямой параллелепипеды, вспомним свойства их противоположных граней и диагоналей параллелепипеда. Затем рассмотрим, что такое прямоугольный параллелепипед, и обсудим его основные свойства.