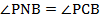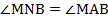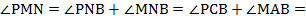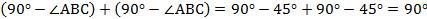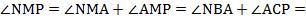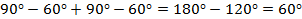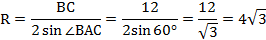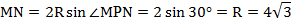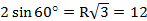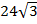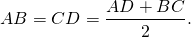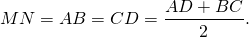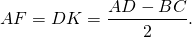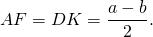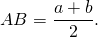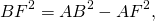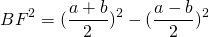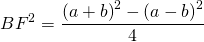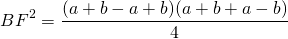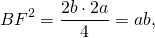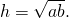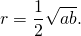В равнобедренную трапецию вписана окружность ch высота

Условие

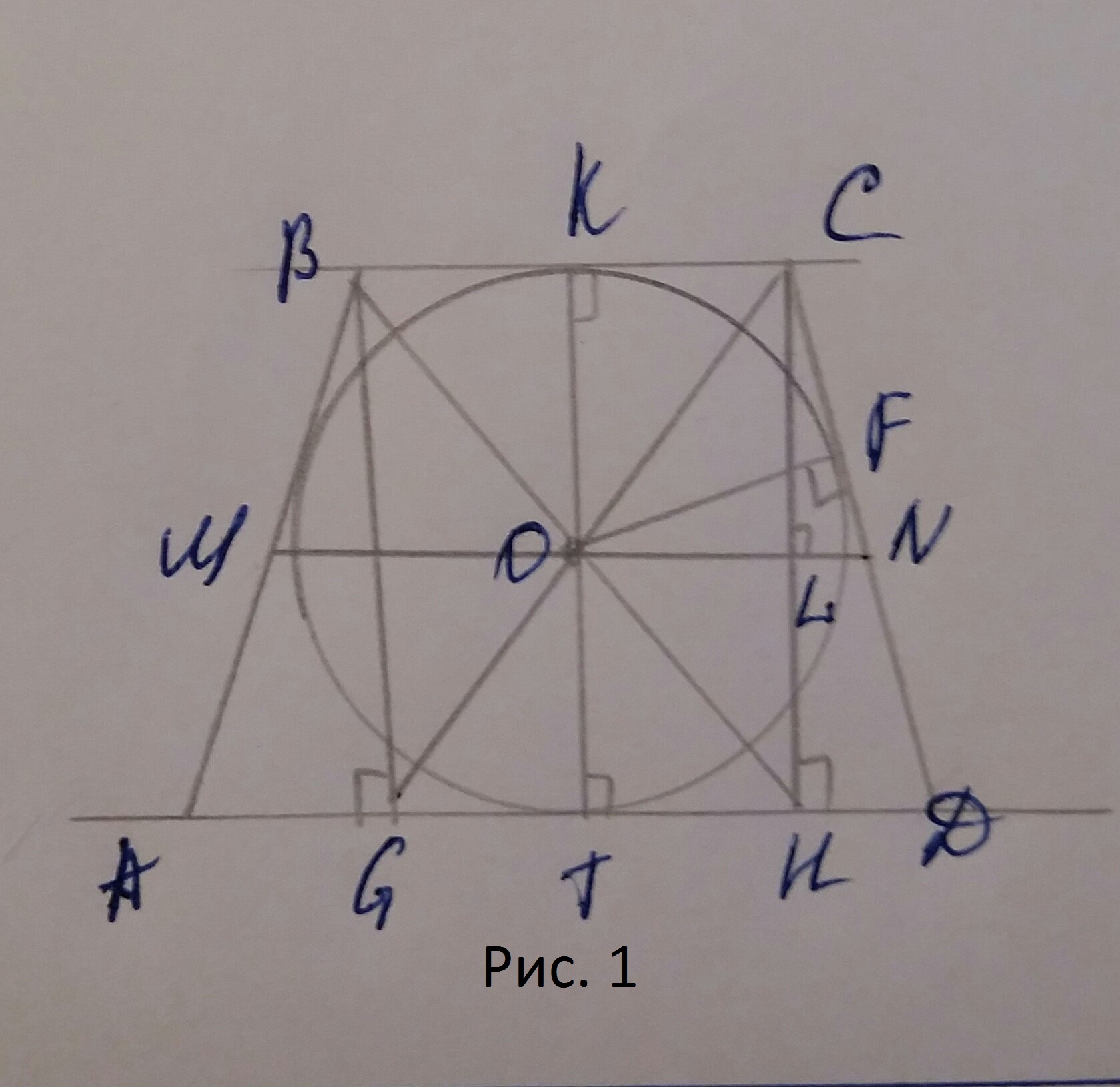
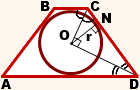
В равнобедренную трапецию ABCD с основаниями AD и BC вписана окружность, CH — высота трапеции.

а) Докажите, что центр окружности, вписанной в трапецию, лежит на отрезке BH.

б) Найдите диагональ AC, если известно, что средняя линия трапеции равна 2sqrt(7), а угол AOD=120 градусов, где O — центр окружности, вписанной в трапецию, а AD — большее основание.

Решение

а)См. рис. 1
BG⊥AD; GBCH-прямоугольник
Пусть О=BH⋂CG
Докажем, что О-центр вписанной окружности.
KT⊥BC; OK=OT, т.е. О равноудалена от ВС и AD.
MN-средняя линия трапеции,
MN=CD по свойству описанной равнобедренной трапеции.
Тогда, ON=CN
⇒ △ONC-равнобедренный,
OF и CL его высоты, проведенные к равным сторонам,
⇒ OF=CL=KO, т.е. О равноудалена от BC,CD, AD(аналогично и от AB).
Значит, О-центр вписанной окружности и О∈ВН.

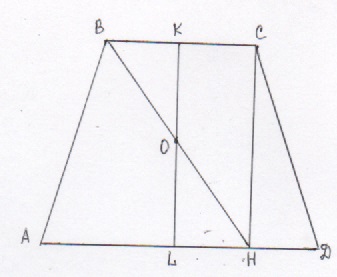
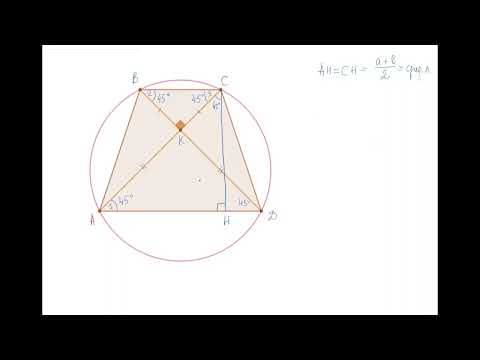
б)См. рис. 2
По свойству описанной равнобедренной трапеции CD=MN=2sqrt(7)
Из △AOD: ∠ADO=(180°-120°):2=30°.
∠ODC=∠ADO=30°(OD-биссектриса).
Из △CHD: ∠DCH=90°-60°=30°, ⇒HD=1/2*CD=1/2*2sqrt(7)=sqrt(7), по теореме Пифагора: CH=sqrt((2sqrt(7))^2-(sqrt(7))^2)=sqrt(28-7)=sqrt(21).
Так как трапеция описано около окружности AD+ВС=AB+CD=2sqrt(7)+2sqrt(7)=4sqrt(7)
AD=2HD+BC
Тогда, 2HD+BC+BC=4sqrt(7)
2BC=4sqrt(7)-2sqrt(7)
2BC=2sqrt(7)
BC=sqrt(7)
⇒ AH=sqrt(7)+sqrt(7)=2sqrt(7).
По теореме Пифагора из △АСН: АС=sqrt((sqrt(21))^2+(2sqrt(7))^2)=sqrt(21+28)=sqrt(49)=7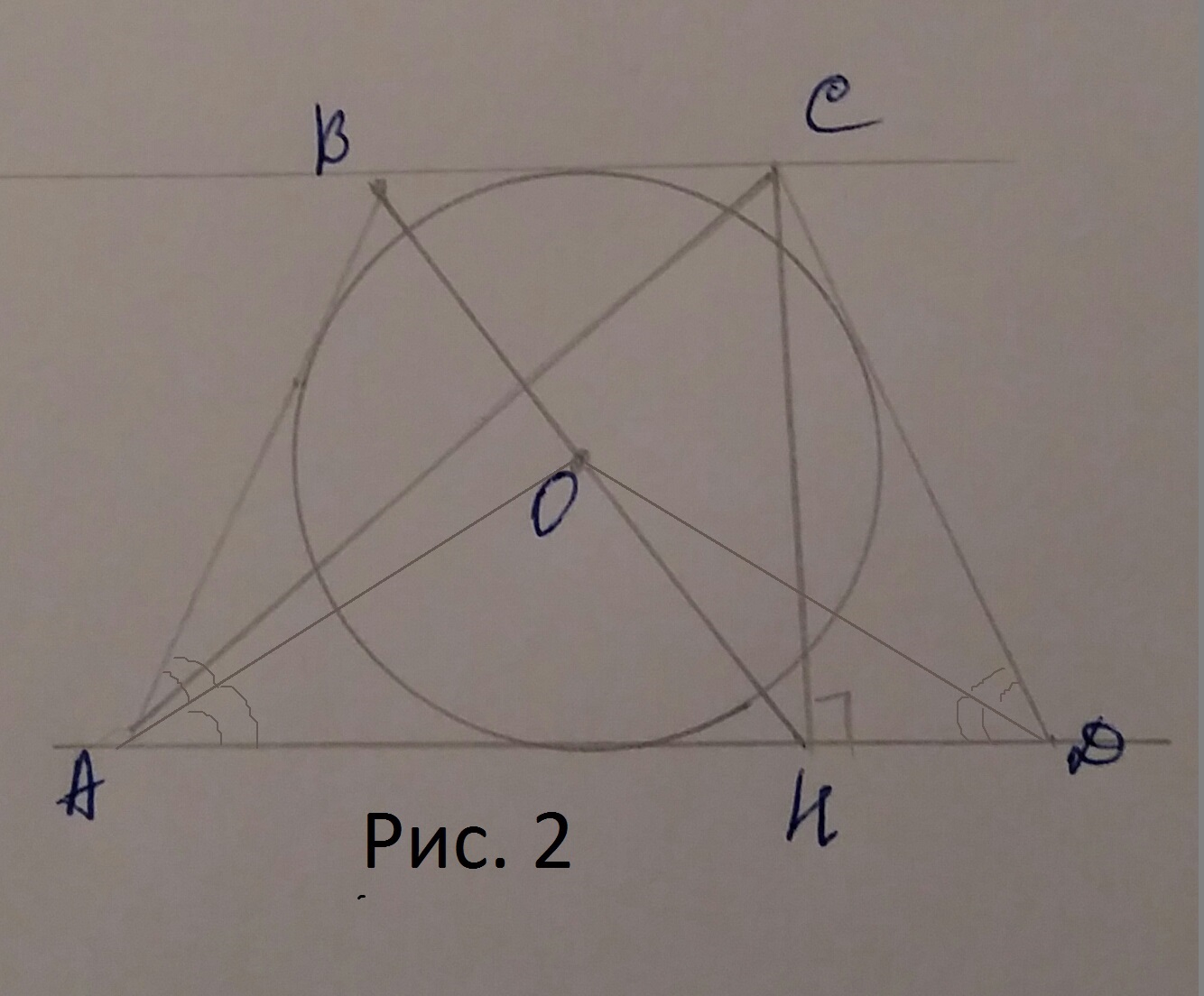

Видео:Задача про трапецию, описанную около окружностиСкачать

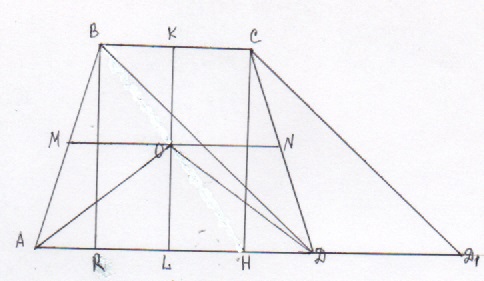
Задача 4 (описанный четырехугольник).

В равнобедренную трапецию АВСD с основаниями AD и ВС вписана окружность, СН – высота трапеции.

а) Доказать, что центр окружности, вписанной в трапецию, лежит на отрезке ВН.

б) Найдите диагональ АС, если известно, что средняя линия трапеции равна 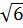, а угол AOD равен 135°, где О – центр окружности, вписанной в трапецию, AD – большее основание.

а) 1) Пусть точки K и L – точки касания окружности оснований трапеции, тогда

2) ΔBOK=ΔHOL по катету(см. пункт 1) и острому углу (углы OBK и LHO равны как накрест лежащие при BC II AD и секущей BH. Поэтому ВО = ОН.

3) Центр вписанной в трапецию окружности лежит на пересечении биссектрис внутренних углов трапеции. Данная трапеция ABCD – равнобедренная, поэтому углы ОВК и ОСК равны. Значит, треугольники ΔВОК и ΔСОК равны (по катету и острому углу)

4) Из 2) и 3) следует, что ВО=ОС=ОН. Точка О равноудалена от вершин прямоугольного треугольника ΔВСН. О – центр описанной около треугольника окружности. Следовательно О принадлежит ВН (его середина). Пункт а) доказан.

б) Для доказательства пункта б) сделаем дополнительный чертеж

1) Пусть MN – средняя линия трапеции. Точка О принадлежит MN и О – её середина, поэтому МО =

2) АО – биссектриса, углы МАО и RAO равны, углы RAO и МОА раны как накрест лежащие. ΔАМО – равнобедренный, АМ=МО= 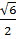. Тогда АВ = 2АМ=

3) ∠AOD=135° (по условию), ∠OAD+∠ODA=45°. Значит, ∠BAD=∠CDA=45°. Пусть BR перпендикулярен AD. BR = AR=

4) Пусть CD₁ II BD и точка D₁ лежит на прямой AD. Четырехугольник ВСD₁D – параллелограмм. CD₁=BD (противоположные стороны), BD=AC(диагонали равнобедренной трапеции). Тогда СD₁=BD=AC.

5) ₁ – равнобедренный, AD₁ – основание. АD₁=AD+DD₁=AD+BC=2MN=2 . CH=BR= . По теореме Пифагора из ΔCHА: AC= = 2 = = 3

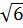
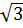
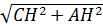
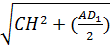
Задача 5

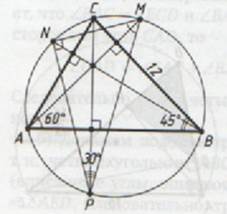
В треугольнике АВС угол ВАС равен 60 ° , угол АВС равен 45 ° . Продолжения высот треугольника АВС пересекают описанную около него окружность в точках M, N, P.

а) Докажите, что треугольник MNP прямоугольный.

б) Найдите площадь треугольника MNP, если ВС=12.

Повторить. Свойство вписанных углов; теорему синусов.

а) Пусть продолжения высот треугольника АВС, проведенных из вершин А, В и С, пересекают описанную около него окружность в точках M, N и P соответственно.

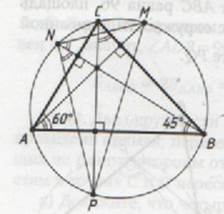
Тогда вписанные углы PNB и PCB опираются на одну и ту же дугу, поэтому

Аналогично,

Следовательно, треугольник MNP прямоугольный. Пункт а) доказан.

б) Угол MNA равен углу NBA , угол APM равен углу ACP (вписанные углы, опирающиеся на одну дугу).

Тогда

Следовательно, 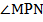= 30 ° .

Пусть R – радиус описанной окружности треугольника АВС. По теореме синусов

Тогда

=

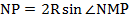
Следовательно,
Ответ:

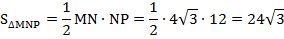
Видео:4.43.1. Планиметрия. Гордин Р.К.Скачать

Вписанная в равнобедренную трапецию окружность

Какими свойствами обладает вписанная в равнобедренную трапецию окружность?

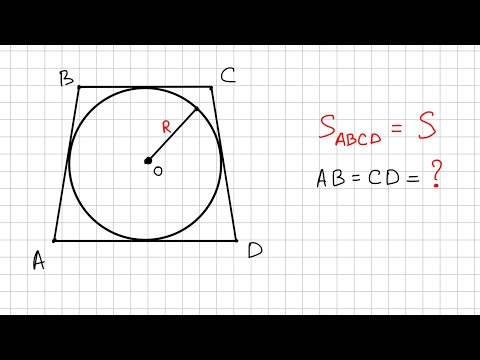
1. В трапецию можно вписать окружность тогда и только тогда, когда суммы длин её противоположных сторон равны.

То есть, в трапецию ABCD можно вписать окружность, если AD+BC=AB+CD.

И обратно, если для трапеции ABCD верно равенство AD+BC=AB+CD, то в неё можно вписать окружность.

Таким образом, если трапеция ABCD — равнобедренная, AD||BC, то её боковые стороны равны полусумме оснований:

2. Отсюда, по свойству средней линии трапеции, боковые стороны равнобедренной трапеции, в которую можно вписать окружность, равны её средней линии.

Если MN —

3. Высота равнобедренной трапеции, в которую можно вписать окружность, равна среднему пропорциональному (среднему геометрическому) между её основаниями.

По свойству равнобедренной трапеции,

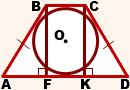
Из прямоугольного треугольника ABF по теореме Пифагора

4. Так как радиус вписанной в трапецию окружности равен половине высоты трапеции, то для равнобедренной трапеции верно равенство

5. В равнобедренной трапеции точки касания делят стороны на две группы равных отрезков.

6. Центр вписанной в равнобедренную трапецию окружности — точка пересечения её биссектрис.

Таким образом, в трапеции ABCD, AD||BC, CO и DO — биссектрисы углов ADC и BCD,

🎦 Видео

Окружность вписана в равнобедренную трапецию. Теорема в задаче. Геометрия, ОГЭ, ЕГЭ. Высота и радиусСкачать

Геометрия Равнобокая трапеция вписана в окружность, центр которой принадлежит одному из основанияСкачать

Малоизвестные свойства равнобедренной трапеции. Разбор задачи 17 ЕГЭ профиль.Скачать

Задача 6 №27926 ЕГЭ по математике. Урок 141Скачать

Основания равнобедренной трапеции равны 72 и 30. Центр окружности, описанной около трапеции... (ЕГЭ)Скачать

В равнобедренной трапеции диагонали перпендикулярны. Высота трапеции равна 12.Скачать

Трапеция. Практическая часть - решение задачи. 8 класс.Скачать

ЕГЭ Задание 16 Равнобедренная трапецияСкачать

В равнобедренной трапеции известна высота ... | ОГЭ 2017 | ЗАДАНИЕ 11 | ШКОЛА ПИФАГОРАСкачать

Геометрия Задача № 26 Найти радиус вписанной в трапецию окружностиСкачать

ОГЭ задачи про трапецию. Решу ОГЭ, Ященко. Задания 16, 18Скачать

Окружность, вписанная в трапециюСкачать

Высота равнобедренной трапеции, проведённая ... | ОГЭ 2017 | ЗАДАНИЕ 11 | ШКОЛА ПИФАГОРАСкачать

Планиметрия 9 | mathus.ru | Высота трапецииСкачать

ТРАПЕЦИЯ — Что такое трапеция, Виды Трапеций, Площадь Трапеции // Геометрия 8 классСкачать

Задание из ЕГЭ: трапеция в окружности #геометрия #егэ2023 #трапеция #окружностьСкачать

Геометрия Трапеция ABCD вписана в окружность с диаметром AD. Найдите высоту трапеции, если радиусСкачать

Вписанные и описанные окружности. Вебинар | МатематикаСкачать