- Ответы в виде таблицы. Сколько диагоналей имеют треугольная, четырёхугольная, шестиугольная и n-угольная призмы?
- Правильная четырехугольная призма
- Правильная четырехугольная призма
- Элементы правильной четырехугольной призмы
- Свойства правильной четырехугольной призмы
- Формулы для правильной четырехугольной призмы
- Указания к решению задач
- Задача.
- Задача
- 💥 Видео
Видео:Геометрия Сколько диагоналей можно провести: 1) в девятиугольнике; 2) в двадцатиугольныеСкачать

Ответы в виде таблицы.
Сколько диагоналей имеют треугольная, четырёхугольная,
шестиугольная и n-угольная
призмы?
Сколько диагональных сечений можно провести через одно
боковое ребро в треугольной, четырёхугольной, шестиугольной и n-угольной призме?
В правильной шестиугольной призме сторона основания равна m, а боковые грани –
квадраты. Найдите диагонали призмы и площади диагоналей сечений.
Формула количества диагоналей у призмы N = n·(n – 3)
где n — количество сторон
треугольная призма- N= 3(3-3)= 0 (диагоналей нет)
четырёхугольная- N=4(4-3)=4
шестиугольная N=6(6-3)=18
n-угольная N=n(n-3)
Сколько диагональных сечений можно провести через одно
боковое ребро в треугольной, четырёхугольной, шестиугольной и n-угольной призме?
в труеуг.-нельзя
четырех.-N=n(n-3)/2=2
шестиуг.-N=6(6-3)/2=9
n-угольной N=n(n-3)/2
Если ответ по предмету Алгебра отсутствует или он оказался неправильным, то попробуй воспользоваться поиском других ответов во всей базе сайта.
Видео:Задача о вычислении диагонали четырёхугольной призмыСкачать

Правильная четырехугольная призма
Четырехугольная призма — это многогранник, две грани которого являются равными квадратами, лежащими в параллельных плоскостях, а остальные грани (боковые грани) — параллелограммами, имеющими общие стороны с этими квадратами.
Правильная четырехугольная призма — это четырехугольная призма у которой основания квадраты, а боковые грани прямоугольники.
Данное геометрическое тело по своим свойствам и характеристикам соответствует — параллелепипеду.
Основания призмы являются равными квадратами.
Боковые грани призмы являются прямоугольниками.
Боковые рёбра призмы параллельны и равны.
Размеры призмы можно выразить через длину стороны a и высоту h.
Площадь полной поверхности призмы равна сумме площади её боковой поверхности и удвоенной площади основания.
Формула площади поверхности четырехугольной призмы:
Видео:№226. В правильной четырехугольной призме через диагональ основания проведено сечениеСкачать
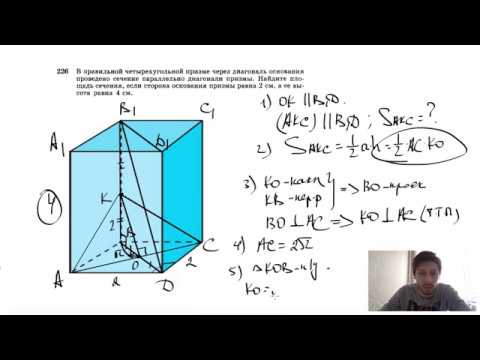
Правильная четырехугольная призма
Видео:СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать

Элементы правильной четырехугольной призмы
- Основания ABCD и A1B1C1D1 равны и параллельны друг другу
- Боковые грани AA1D1D, AA1B1B, BB1C1C и CC1D1D, каждая из которых является прямоугольником
- Боковая поверхность — сумма площадей всех боковых граней призмы
- Полная поверхность — сумма площадей всех оснований и боковых граней (сумма площади боковой поверхности и оснований)
- Боковые ребра AA1, BB1, CC1 и DD1.
- Диагональ B1D
- Диагональ основания BD
- Диагональное сечение BB1D1D
- Перпендикулярное сечение A2B2C2D2 .
Видео:Диагонали в многоугольниках. Есть ли зависимость между количеством вершин и диагоналей в n-угольникеСкачать

Свойства правильной четырехугольной призмы
- Основаниями являются два равных квадрата
- Основания параллельны друг другу
- Боковыми гранями являются прямоугольники
- Боковые грани равны между собой
- Боковые грани перпендикулярны основаниям
- Боковые ребра параллельны между собой и равны
- Перпендикулярное сечение перпендикулярно всем боковым ребрам и параллельно основаниям
- Углы перпендикулярного сечения — прямые
- Диагональное сечение правильной четырехугольной призмы представляет собой прямоугольник
- Перпендикулярное (ортогональное сечение) параллельно основаниям
Видео:Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Формулы для правильной четырехугольной призмы
Видео:№224. Диагональ правильной четырехугольной призмы наклонена к плоскости основания под углом 60°Скачать
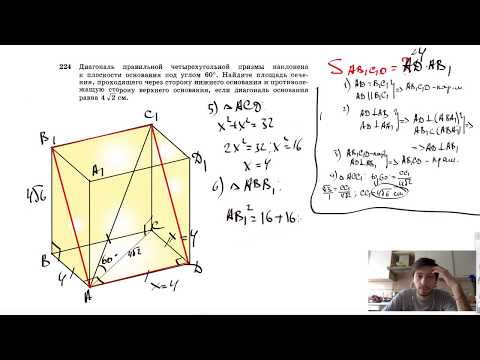
Указания к решению задач
При решении задач на тему «правильная четырехугольная призма» подразумевается, что:
Правильная призма — призма в основании которой лежит правильный многоугольник, а боковые ребра перпендикулярны плоскостям основания. То есть правильная четырехугольная призма содержит в своем основании квадрат. (см. выше свойства правильной четырехугольной призмы)
Видео:#115. Задание 8: четырехугольная призмаСкачать

Задача.
В правильной четырёхугольной призме площадь основания 144 см 2 , а высота 14 см. Найти диагональ призмы и площадь полной поверхности.
Решение.
Правильный четырехугольник — это квадрат.
Соответственно, сторона основания будет равна √ 144 = 12 см.
Откуда диагональ основания правильной прямоугольной призмы будет равна
√( 12 2 + 12 2 ) = √288 = 12√2
Диагональ правильной призмы образует с диагональю основания и высотой призмы прямоугольный треугольник. Соответственно, по теореме Пифагора диагональ заданной правильной четырехугольной призмы будет равна:
√( ( 12√2 ) 2 + 14 2 ) = 22 см
Видео:10 класс, 30 урок, ПризмаСкачать

Задача
Определите полную поверхность правильной четырехугольной призмы, если ее диагональ равна 5 см, а диагональ боковой грани равна 4 см.
Решение.
Поскольку в основании правильной четырехугольной призмы лежит квадрат, то сторону основания (обозначим как a) найдем по теореме Пифагора:
a 2 + a 2 = 5 2
2a 2 = 25
a = √12,5
Высота боковой грани (обозначим как h) тогда будет равна:
h 2 + 12,5 = 4 2
h 2 + 12,5 = 16
h 2 = 3,5
h = √3,5
Площадь полной поверхности будет равна сумме площади боковой поверхности и удвоенной площади основания
S = 2a 2 + 4ah
S = 25 + 4√12,5 * √3,5
S = 25 + 4√43,75
S = 25 + 4√(175/4)
S = 25 + 4√(7*25/4)
S = 25 + 10√7 ≈ 51,46 см 2 .
💥 Видео
Как вывести формулу количества диагоналей многоугольника. Сумма диагоналей n-угольника. Формула Dn.Скачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

№225. Диагональ правильной четырехугольной призмы образует с плоскостью боковой грани угол в 30°.Скачать
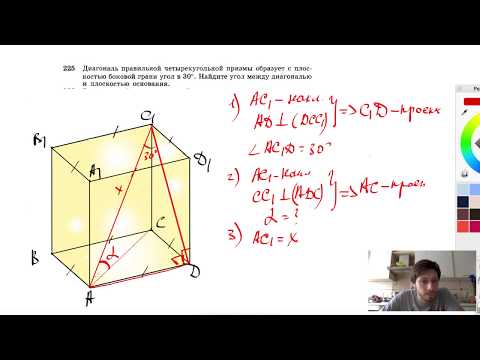
Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

8 класс, 3 урок, ЧетырехугольникСкачать

24 Количество диагоналей выпуклого n-угольникаСкачать

Диагонали четырехугольника равны 4 и 5.Скачать

№529. Диагонали четырехугольника равны 16 см и 20 см и пересекаются под углом в 30°. Найдите площадьСкачать
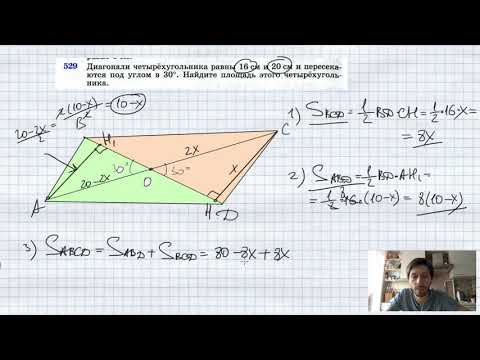
Геометрия 8. Урок 12 - Площадь четырехугольников. Формулы.Скачать

8 класс, 2 урок, Выпуклый многоугольникСкачать

сечение в четырехугольной призмеСкачать









