Линейно зависимы ли векторы в R 4 ?
Составим линейную комбинацию векторов a1, a2, a3, a4:
α1a1 + α2a2 + α3a3 + α4a4.
Чтобы выяснить, являются ли векторы a1, a2, a3, a4 линейно зависимыми или нет, достаточно определить, сколько решений имеет уравнение
α1a1 + α2a2 + α3a3 + α4a4 = 0, где в качестве неизвестных выступают коэффициенты α1, α2, α3, α4. Если это уравнение имеет единственное решение (нулевое решение есть всегда), то векторы линейно независимы. Если у уравнения есть ненулевое решение, то векторы линейно зависимы.
Подставим числовые значения векторов a1, a2, a3, a4, получим:
α1(4, −5, 2, 6) + α2(2, −2, 1, 3) + α3(6, −3, 3, 9) + α4(4, −1, 5, 6) = (0, 0, 0, 0).
Умножим каждый из векторов на свой коэффициент и сложим все векторы в левой части равенства, получим:
(4α1 + 2α2 + 6α3 + 4α4, −5α1 − 2α2 − 3α3 − α4, 2α1 + α2 + 3α3 + 5α4, 6α1 + 3α2 + 9α3 + 6α4) = (0, 0, 0, 0).
Два вектора равны, если равны их соответствующие компоненты. Следовательно полученное равенство векторов равносильно системе:
Найдем число решений этой системы, используя метод Гаусса. Матрица коэффициентов имеет вид:
Заметим, что столбцы матрицы коэффициентов — это в точности данные четыре вектора. Мы не пишем столбец со свободными членами, так как все они равны нулю и при элементарных преобразованиях строк не меняются. Приведем матрицу к ступенчатому виду:
Полученная матрица состоит из трех строк и четырех столбцов. Исходная система линейных уравнений имеет ненулевое решение. Следовательно данные векторы a1, a2, a3, a4 линейно зависимы.
Ответ. Векторы a1, a2, a3, a4 линейно зависимы.
- Линейная зависимость системы векторов. Коллинеарные векторы
- Коллинеарные векторы
- Условия коллинеарности векторов
- Примеры задач на исследование коллинеарности векторов
- Критерии линейной зависимости и линейной независимости систем векторов
- Свойства линейно зависимых векторов
- Примеры решения задач на линейную зависимость или линейную независимость векторов
- Глава VII
- 1. Арифметическое пространство R n
- 2. Линейные операции
- 3. Действия над векторами, заданными в координатной форме
- 4. Скалярное произведение векторов
- 5. Системы векторов
- 6. Разложение вектора по системе векторов
- 7. Линейные преобразования
- 8. Характеристические корни и собственные значения
- 💡 Видео
Видео:Линейная зависимость и линейная независимость. ТемаСкачать

Линейная зависимость системы векторов. Коллинеарные векторы
В данной статье мы расскажем:
- что такое коллинеарные векторы;
- какие существуют условия коллинеарности векторов;
- какие существуют свойства коллинеарных векторов;
- что такое линейная зависимость коллинеарных векторов.
Видео:Доказать, что векторы a, b, c образуют базис и найти координаты вектора d в этом базисеСкачать

Коллинеарные векторы
Коллинеарные векторы — это векторы, которые являются параллелями одной прямой или лежат на одной прямой.
Видео:Линейная зависимость и линейная независимость векторов.Скачать

Условия коллинеарности векторов
Два векторы являются коллинеарными, если выполняется любое из следующих условий:
- условие 1. Векторы a и b коллинеарны при наличии такого числа λ , что a = λ b ;
- условие 2. Векторы a и b коллинеарны при равном отношении координат:
a = ( a 1 ; a 2 ) , b = ( b 1 ; b 2 ) ⇒ a ∥ b ⇔ a 1 b 1 = a 2 b 2
- условие 3. Векторы a и b коллинеарны при условии равенства векторного произведения и нулевого вектора:
Условие 2 неприменимо, если одна из координат вектора равна нулю.
Условие 3 применимо только к тем векторам, которые заданы в пространстве.
Видео:Линейная зависимость векторов. РангСкачать

Примеры задач на исследование коллинеарности векторов
Исследуем векторы а = ( 1 ; 3 ) и b = ( 2 ; 1 ) на коллинеарность.
В данном случае необходимо воспользоваться 2-м условием коллинеарности. Для заданных векторов оно выглядит так:
Равенство неверное. Отсюда можно сделать вывод, что векторы a и b неколлинеарны.
Ответ: a | | b
Какое значение m вектора a = ( 1 ; 2 ) и b = ( — 1 ; m ) необходимо для коллинеарности векторов?
Используя второе условие коллинераности, векторы будут коллинеарными, если их координаты будут пропорциональными:
Отсюда видно, что m = — 2 .
Ответ: m = — 2 .
Видео:Как разложить вектор по базису - bezbotvyСкачать

Критерии линейной зависимости и линейной независимости систем векторов
Система векторов векторного пространства линейно зависима только в том случае, когда один из векторов системы можно выразить через остальные векторы данной системы.
Пусть система e 1 , e 2 , . . . , e n является линейно зависимой. Запишем линейную комбинацию этой системы равную нулевому вектору:
a 1 e 1 + a 2 e 2 + . . . + a n e n = 0
в которой хотя бы один из коэффициентов комбинации не равен нулю.
Пусть a k ≠ 0 k ∈ 1 , 2 , . . . , n .
Делим обе части равенства на ненулевой коэффициент:
a k — 1 ( a k — 1 a 1 ) e 1 + ( a k — 1 a k ) e k + . . . + ( a k — 1 a n ) e n = 0
— a k — 1 a m , где m ∈ 1 , 2 , . . . , k — 1 , k + 1 , n
β 1 e 1 + . . . + β k — 1 e k — 1 + β k + 1 e k + 1 + . . . + β n e n = 0
или e k = ( — β 1 ) e 1 + . . . + ( — β k — 1 ) e k — 1 + ( — β k + 1 ) e k + 1 + . . . + ( — β n ) e n
Отсюда следует, что один из векторов системы выражается через все остальные векторы системы. Что и требовалось доказать (ч.т.д.).
Пусть один из векторов можно линейно выразить через все остальные векторы системы:
e k = γ 1 e 1 + . . . + γ k — 1 e k — 1 + γ k + 1 e k + 1 + . . . + γ n e n
Переносим вектор e k в правую часть этого равенства:
0 = γ 1 e 1 + . . . + γ k — 1 e k — 1 — e k + γ k + 1 e k + 1 + . . . + γ n e n
Поскольку коэффициент вектора e k равен — 1 ≠ 0 , у нас получается нетривиальное представление нуля системой векторов e 1 , e 2 , . . . , e n , а это, в свою очередь, означает, что данная система векторов линейно зависима. Что и требовалось доказать (ч.т.д.).
- Система векторов является линейно независимой, когда ни один из ее векторов нельзя выразить через все остальные векторы системы.
- Система векторов, которая содержит нулевой вектор или два равных вектора, линейно зависима.
Видео:Высшая математика. Линейные пространства. Векторы. БазисСкачать

Свойства линейно зависимых векторов
- Для 2-х и 3-х мерных векторов выполняется условие: два линейно зависимых вектора — коллинеарны. Два коллинеарных вектора — линейно зависимы.
- Для 3-х мерных векторов выполняется условие: три линейно зависимые вектора — компланарны. (3 компланарных вектора — линейно зависимы).
- Для n-мерных векторов выполняется условие: n + 1 вектор всегда линейно зависимы.
Видео:Линейная зависимость векторов на примерахСкачать

Примеры решения задач на линейную зависимость или линейную независимость векторов
Проверим векторы a = 3 , 4 , 5 , b = — 3 , 0 , 5 , c = 4 , 4 , 4 , d = 3 , 4 , 0 на линейную независимость.
Решение. Векторы являются линейно зависимыми, поскольку размерность векторов меньше количества векторов.
Проверим векторы a = 1 , 1 , 1 , b = 1 , 2 , 0 , c = 0 , — 1 , 1 на линейную независимость.
Решение. Находим значения коэффициентов, при которых линейная комбинация будет равняться нулевому вектору:
x 1 a + x 2 b + x 3 c 1 = 0
Записываем векторное уравнение в виде линейного:
x 1 + x 2 = 0 x 1 + 2 x 2 — x 3 = 0 x 1 + x 3 = 0
Решаем эту систему при помощи метода Гаусса:
1 1 0 | 0 1 2 — 1 | 0 1 0 1 | 0
Из 2-ой строки вычитаем 1-ю, из 3-ей — 1-ю:
1 1 0 | 0 1 — 1 2 — 1 — 1 — 0 | 0 — 0 1 — 1 0 — 1 1 — 0 | 0 — 0
1 1 0 | 0 0 1 — 1 | 0 0 — 1 1 | 0
Из 1-й строки вычитаем 2-ю, к 3-ей прибавляем 2-ю:
1 — 0 1 — 1 0 — ( — 1 ) | 0 — 0 0 1 — 1 | 0 0 + 0 — 1 + 1 1 + ( — 1 ) | 0 + 0
0 1 0 | 1 0 1 — 1 | 0 0 0 0 | 0
Из решения следует, что у системы множество решений. Это значит, что существует ненулевая комбинация значения таких чисел x 1 , x 2 , x 3 , при которых линейная комбинация a , b , c равняется нулевому вектору. Следовательно, векторы a , b , c являются линейно зависимыми.
Видео:Линейная зависимость векторовСкачать

Глава VII
Видео:Лекция 16. Понятие вектора и векторного пространства. Базис векторного пространства.Скачать

1. Арифметическое пространство R n
Величина, которая полностью характеризуется своим числовым значением в выбранной системе единиц, называется скалярной или скаляром (масса, объем, температура). Скаляр определяется числом, положительным, отрицательным или равным нулю. Если величина характеризуется еще и направлением, то она называется векторной или вектором (сила, скорость и так далее). Таким образом, вектор определяется числом и направлением.
Многие вопросы как теоретического, так и прикладного характера приводят к рассмотрению упорядоченных совокупностей чисел (величин). Например, план работы предприятия, выраженный в определенных числовых показателях, рост цен за ряд лет и так далее. Если отвлечься от конкретного смысла объектов, мы приходим к следующему понятию.
Определение 1.1. Множество всех упорядоченных совокупностей по n чисел (х1,х2. хn) называется арифметическим n-мерным пространством ( R n )
(n — размерность пространства).
Будем теперь предполагать, что на плоскости или в пространстве всегда фиксирована некоторая прямоугольная система декартовых координат. Тогда каждая точка будет определена своими координатами А(х1,х2. хn), В(у1,у2. уn).
Арифметическое пространство R 1 (или R) образует множество действительных чисел. R 2 представляет собой плоскость, при этом имеем

R 3 — это трехмерное пространство; при этом имеем

В случае R n мы имеем дело с n-мерным пространством и тогда

Определение 1.2. Совокупность точек n-мерного пространства, для которых определено расстояние по формуле (1.1), называется n-мерным Евклидовым пространством.
Свойства расстояния между двумя точками:
1. r (А,В) ³ 0, причем если r (А,В) = 0, следовательно, А = В.
2. r (А,В) = r (В,А) для всех точек А, В Î R n ,
3. r (А,C) £ r (A,В) + r (B,C) для всех точек А, В, C Î R n ,
Рассмотрим более подробно понятие вектора.
Для определения положения точки на прямой построим систему координат:
1) возьмем на прямой произвольную точку О и назовем ее началом координат;
2) примем какой-нибудь отрезок (ОЕ = е) за единицу масштаба;
3) выберем положительное направление.
Теперь положение любой точки М будет определяться числом 
Примем следующее обозначение: х- координата точки М, что будем записывать как М(х). Тогда

то есть точка считается заданной, если известна ее координата. В дальнейшем если будем говорить о точке, то будем иметь ввиду число (координату точки) и наоборот, таким образом, установлено взаимно-однозначное соответствие.
Определение 1.3. Отрезок, у которого указаны начало и конец, называется направленным отрезком или вектором.
Для этого понятия вводятся следующие обозначения: модуль вектора —


Видео:§44 Линейная независимость векторовСкачать

2. Линейные операции
1. Введем понятие о векторе О, модуль которого равен 0 (направление произвольно).
2. 

3. 

а) переместительное свойство

б) сочетательное свойство





4. 
5. 


Определение 2.1. Два вектора 

Теорема 2.1. Для того чтобы два вектора 


Определение 2.2. Три вектора 


Теорема 2.2. Чтобы три ненулевых вектора 



Определение 2.3. Под декартовыми прямоугольными координатами x, y, z точки М будем понимать проекцию ее радиус-вектора на соответствующие оси координат.
То есть в пространстве для каждой точки М существует ее радиус-вектор 

Пусть задан вектор 
то есть 

Видео:Линейно зависимые векторы: как доказать?Скачать

 3. Действия над векторами, заданными в координатной форме
3. Действия над векторами, заданными в координатной форме
Пусть 
Введем в рассмотрение единичные векторы (орты) 




Теперь введем линейные операции над векторами в следующем виде:
1.

2. 
Видео:Примеры Линейная зависимость векторов Базис и ранг системы векторовСкачать

4. Скалярное произведение векторов
Определение 4.1. Под скалярным произведением двух векторов 





Или в координатной форме

Но тогда, используя определение (7.7), можно вывести формулу для нахождения угла между векторами

Видео:Линейная зависимость и независимость систем векторовСкачать

5. Системы векторов
Определение 5.1. Множество L с определенными для его элементов операциями сложения и умножения на число, удовлетворяющими следующим аксиомам
2. (х + у) + z = x + (y + z)
3. существует элемент 0 такой, что х + 0 = х
4. для любого элемента х существует такой элемент -х,
6. b × ( a × х) = ( b × a ) × х
7. ( a + b ) × х = a × х + b × х
8. a × (х + у) = a × х + b × у
называется линейным (векторным) пространством, а его элементы — векторами.
1. Множество всех векторов пространства.
2. Множество всех векторов, принадлежащих плоскости или параллельных ей.
3. Множество многочленов (любых степеней).
называется линейной комбинацией векторов а1, а2. аn с коэффициентами х1, х2, . хn.
Очевидно, что любая комбинация векторов некоторого линейного пространства
представляет собой вектор этого же пространства. Если некоторый вектор можно представить в виде
то говорят, что вектор b разложен по векторам а1, а2. аn.
По двум неколлинеарным векторам можно разложить любой вектор, лежащий с ними в одной плоскости.
Важную роль в теории линейных пространств играет понятие линейной зависимости и независимости векторов.
Система векторов а1, а2. аn пространства L называется линейно независимой, если
имеет место, когда хi = 0 (i = 1 ÷ n), а если хотя бы один из коэффициентов отличен от нуля, то система векторов называется линейно зависимой.
Система n линейно независимых векторов в n- мерном пространстве называется базисом этого пространства.
Пусть а1, а2, . аn образуют базис, а b — произвольный вектор этого же пространства, тогда система
будет зависима, так как из того, что
следует, что l n+1 ¹ 0, следовательно,
Это разложение будет единственным.
Пусть это не так, то есть
то есть разложения совпадают.
Коэффициенты разложения вектора называются координатами вектора в данном базисе.
Видео:Линейная оболочка. Базис и размерностьСкачать

6. Разложение вектора по системе векторов
Легко можно показать, что R n можно рассматривать как линейное пространство, а его элементы считать векторами.
Будем обозначать элементы пространства через Х(х1, х2, . хn), а числа х1, х2, . хn назовем компонентами вектора Х.
Нуль-вектором считаем вектор, все компоненты которого равны нулю 0(0,0. 0). Но элементы R n можно интерпретировать как однострочные (или одностолбцовые) матрицы. И тогда R n будет линейным пространством таких матриц. (Смотри операции над матрицами, равенство, сложение, умножение).
Пусть теперь мы имеем k векторов (систему векторов) аj(а1j,а2j. аkj) ( j = 1,2. k); их компоненты аij имеют два индекса: i — номер компоненты данного вектора, j — номер вектора в системе.
Пусть дан еще вектор b(b1,b2. bn). В силу определения равенства векторов и действий между ними мы можем записать

Это равенство можно записать в виде системы n линейных уравнений с k переменными

Компоненты вектора аj образуют столбец коэффициентов при переменной хj в этой системе, а компоненты вектора b — столбец свободных членов. Верно и обратное: если в произвольно заданной системе линейных уравнений (6.2) совокупности коэффициентов при одной и той же переменной и свободные члены интерпретировать как соответствующие k векторы , то мы придем к векторному уравнению (6.1).
Уравнение (6.1) называется векторной формой записи системы линейных уравнений (6.2).
Если система (6.2) несовместна, то разложение вектора b по векторам а1,а2. аk невозможно. Если система (6.2) совместна, то разложение (6.1) возможно, а каждое решение системы (6.2) является совокупностью коэффициентов этого разложения.

есть векторная запись однородной системы линейных уравнений

Система (6.4) всегда совместна, так как имеет нулевое решение; и если это решение единственное, то равенство (6.3) имеет место только при нулевых значениях коэффициентов, то есть система векторов а1,а2. аk линейно независима.
С другой стороны, нулевое решение системы (6.4) будет единственным тогда и только тогда, когда ее ранг равен числу переменных (r = k), или иначе говоря, утверждение “система векторов а1,а2. аk линейно независима” эквивалентно условию по отношению к рангу матрицы

столбцы которой образованы компонентами этих векторов: ранг этой матрицы должен быть равен числу ее столбцов.
Но r £ n, следовательно, если система k векторов линейно независима, то
k = r £ n. (Мы доказали теорему).
Теорема 6.1. В пространстве R n система линейно независимых векторов не может содержать более n векторов.
Теорема 6.2. Любые n векторов, для которых определитель со столбцами, образованными компонентами векторов, не равен 0, будут линейно независимы.
Таким образом если
то векторы будут линейно независимыми (k = n, D ¹ 0, система (6.4) имеет единственное нулевое решение; матрица (6.5) — квадратная, и ранг матрицы r равен n).
Отсюда следует, что размерность линейного пространства равна n.
Векторы, для которых D ¹ 0, образуют базис этого пространства. Решение системы (6.4) является совокупностью координат вектора 
Показать, что векторы а1, а2, а3, а4 образуют базис в R 4 (линейное 4-х мерное пространство) и определить координаты вектора b в этом пространстве.

Так как D ¹ 0, следовательно, векторы а1, а2, а3, а4 образуют базис в R 4 .
Для вычисления координат вектора b в этом базисе составим систему линейных уравнений
Решение этой системы
представляет собой совокупность координат вектора b в базисе а1, а2, а3, а4, то есть b(2, 0, -1, 3) или
З а м е ч а н и е.
Базис в R 4 , как и в любом другом пространстве, может быть выбран не единственным образом.
Векторы еj (j = 1,2. n) образуют базис, если
Проверить самостоятельно, что это базис.
В данном случае координаты вектора являются и его компонентами. ×
Видео:Базис. Разложение вектора по базису.Скачать

7. Линейные преобразования
Пусть дано n-мерное действительное пространство, которое обозначим через Ln. Рассмотрим преобразование этого пространства, переводящее каждый вектор а, принадлежащий Ln, в некоторый вектор а / этого же пространства. Вектор а / назовем образом вектора а при рассматриваемом преобразовании. Условимся, что вместо принятого а / = j (а) будем писать а / = а j .
Определение 7.1. Преобразование j линейного пространства Ln называется линейным преобразованием этого пространства, если:
1. (a + b) j = a j + b j
2. ( a × a) j = a × (a j )
Из определения (7.9) следует, что линейное преобразование Ln переводит любую линейную комбинацию данных векторов а1, а2, . аn в линейную комбинацию с теми же коэффициентами образов этих векторов
Если добавить еще одно условие:
то есть нулевой вектор остается неподвижным,
то можно получить некоторое обозрение всех линейных преобразований линейного пространства Ln.
Пусть е1, е2. еn — база этого пространства. Так как всякий вектор а, принадлежащий Ln, однозначно представим в виде линейной комбинации векторов базы, то согласно (), образ вектора ас теми же коэффициентами выражается через образы векторов базы е1, е2. еn.
Теперь можно показать, что существует взаимно однозначное соответствие между всеми линейными преобразованиями пространства Ln и всеми квадратными матрицами порядка n, то есть
Пусть в базе е1, е2, е3 трехмерного линейного пространства линейное преобразование j задано матрицей
Определение 7.2. Матрицы, задающие одно и то же линейное преобразование в разных базах, подобны между собой. При этом матрица линейного преобразования j в базе е / получается трансформированием матрицы этого преобразования в базе е матрицей перехода от базы е / к базе е.
Пусть матрица А задает линейное преобразование j в базе е. Тогда любая матрица В, подобная матрице А,
также задает преобразование j в некоторой базе, а именно в базе, получающейся при помощи матрицы перехода Q -1 от базы е к базе е / .
Другими словами матрица Т называется матрицей перехода от одной базы к другой , если
е / = Т × е, где Т — матрица перехода.
Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

8. Характеристические корни и собственные значения
Пусть 
где Е — единичная матрица порядка n, которая называется характеристической матрицей матрицы А.
Определитель матрицы А- l × Е будет многочленом от l , причем степени n.
Многочлен n-ной степени 
Теорема 8.1. Подобные матрицы обладают одинаковыми характеристическими многочленами и, следовательно, одинаковыми характеристическими корнями.
Д о к а з а т е л ь с т в о :
Тогда, учитывая, что матрица l × Е перестановочна с матрицей Q, а 

Определение 8.1. Пусть в действительном линейном пространстве Ln задано линейное преобразование j . Если вектор b, отличный от нуля, переводится преобразованием j в вектор, пропорциональный самому b,
где l 0 — некоторое действительное число, то вектор b называется собственным вектором преобразования j , а число l 0 — собственным значением этого преобразования.
З а м е ч а н и е.
0-вектор не является собственным вектором преобразования j .
Теорема 8.2. Действительные характеристические корни линейного преобразования j , если они существуют, (и только они) служат собственными значениями этого преобразования.
З а м е ч а н и е. Хотя линейное преобразование j в разных базах задается различными матрицами, однако все эти матрицы имеют один и тот же набор характеристических корней. Поэтому мы и называем их характеристическими корнями самого преобразования j .
Полное изложение данной темы смотри Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры. — М.: Наука, 1984.

💡 Видео
Примеры линейной зависимости векторов.Скачать
Линейная комбинация векторовСкачать
Линейные комбинации, span и базисные вектора | Сущность Линейной Алгебры, глава 2Скачать

Аналитическая геометрия, 1 урок, Векторы в пространствеСкачать




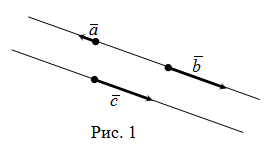








 3. Действия над векторами, заданными в координатной форме
3. Действия над векторами, заданными в координатной форме











