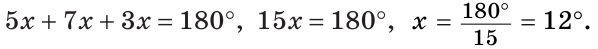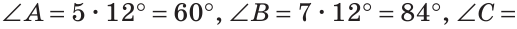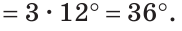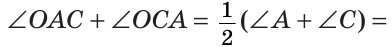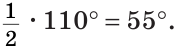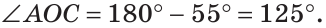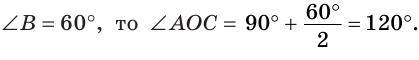Геометрия | 5 — 9 классы
1)Вычислите градусные меры углов треугольника ABC.
B = 180° — 110° = 70°
C = 28° — по условию
А = 180° — 70° — 28° = 82°, т.
К сумма всех углов треугольника равна 180°.
- Между сторонами угла ABC = 110° проходит луч BF?
- Развёрнутый угол ABC разделён лучом BO на два угла?
- Градусные меры двух углов треугольника ABC равны 20 градусов и 70 градусов?
- Вычеслительная градусная меры углов A и C треугольника ABC?
- 1)Вычислите градусные меры углов треугольника?
- Угол при вершине равнобедренного треугольника в 7 раз больше угла при его основании?
- Вычислите градусную меру углов треугольника?
- Градусная мера углов треугольника пропорциональна числам 3, 4 и 5?
- В равнобедренном треугольнике ABC проведены высоты AK и BM, градусная мера угла между которыми равна 100 °?
- В равнобедренном треугольнике градусная мера одного из углов на 78 градусов меньше градусной меры другого угла ?
- Сумма углов треугольника — определение и вычисление с доказательствами и примерами решения
- Решение треугольников онлайн
- Решение треугольника по трем сторонам
- Решение треугольника по двум сторонам и углу между ними
- Решение треугольника по стороне и любым двум углам
- 🔍 Видео
Видео:№224. Найдите углы треугольника ABC, если ∠A:∠B:∠C= 2:3:4.Скачать

Между сторонами угла ABC = 110° проходит луч BF?
Между сторонами угла ABC = 110° проходит луч BF.
Градусная мера угла ABF на 12° меньше градусной меры угла CBF.
Вычислить : а) градусную меру каждого угла, б) градусную меру угла, образованного биссектрисами этих углов.
Видео:9. Градусная мера углаСкачать
Развёрнутый угол ABC разделён лучом BO на два угла?
Развёрнутый угол ABC разделён лучом BO на два угла.
Градусная мера угла ABO на 50° меньше градусной меры угла OBC.
Вычислите градусные меры углов ABO и OBC.
Видео:7 класс, 9 урок, Градусная мера углаСкачать

Градусные меры двух углов треугольника ABC равны 20 градусов и 70 градусов?
Градусные меры двух углов треугольника ABC равны 20 градусов и 70 градусов.
Найдите разность в градусных мер большего и меньшего углов этого треугольника.
Видео:Угол. Градусная мера угла. Практическая часть - решение задачи. 5 класс.Скачать

Вычеслительная градусная меры углов A и C треугольника ABC?
Вычеслительная градусная меры углов A и C треугольника ABC.
Видео:Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать

1)Вычислите градусные меры углов треугольника?
1)Вычислите градусные меры углов треугольника.
Видео:Построение углов заданной градусной мерыСкачать

Угол при вершине равнобедренного треугольника в 7 раз больше угла при его основании?
Угол при вершине равнобедренного треугольника в 7 раз больше угла при его основании.
Вычислите градусные меры всех углов этого треугольника.
Видео:Градусная мера угла. 9 класс.Скачать

Вычислите градусную меру углов треугольника?
Вычислите градусную меру углов треугольника.
Видео:Градусная мера углаСкачать
Градусная мера углов треугольника пропорциональна числам 3, 4 и 5?
Градусная мера углов треугольника пропорциональна числам 3, 4 и 5.
Вычислите градусную меру каждого угла треугольника.
Видео:7 класс, 31 урок, Теорема о сумме углов треугольникаСкачать

В равнобедренном треугольнике ABC проведены высоты AK и BM, градусная мера угла между которыми равна 100 °?
В равнобедренном треугольнике ABC проведены высоты AK и BM, градусная мера угла между которыми равна 100 °.
Найдите градусную меру угла ABC.
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

В равнобедренном треугольнике градусная мера одного из углов на 78 градусов меньше градусной меры другого угла ?
В равнобедренном треугольнике градусная мера одного из углов на 78 градусов меньше градусной меры другого угла .
Найдите градусную меру одного из двух разных углов этого треугольника.
Вы находитесь на странице вопроса 1)Вычислите градусные меры углов треугольника ABC? из категории Геометрия. Уровень сложности вопроса рассчитан на учащихся 5 — 9 классов. На странице можно узнать правильный ответ, сверить его со своим вариантом и обсудить возможные версии с другими пользователями сайта посредством обратной связи. Если ответ вызывает сомнения или покажется вам неполным, для проверки найдите ответы на аналогичные вопросы по теме в этой же категории, или создайте новый вопрос, используя ключевые слова: введите вопрос в поисковую строку, нажав кнопку в верхней части страницы.
100, т. К накрест лежащий углу 80 градусов равен 80 , а Х смежный с ним , те 100.
Видео:Геометрия 7 класс (Урок№5 - Измерение углов.)Скачать

Сумма углов треугольника — определение и вычисление с доказательствами и примерами решения
Сумма углов треугольника:
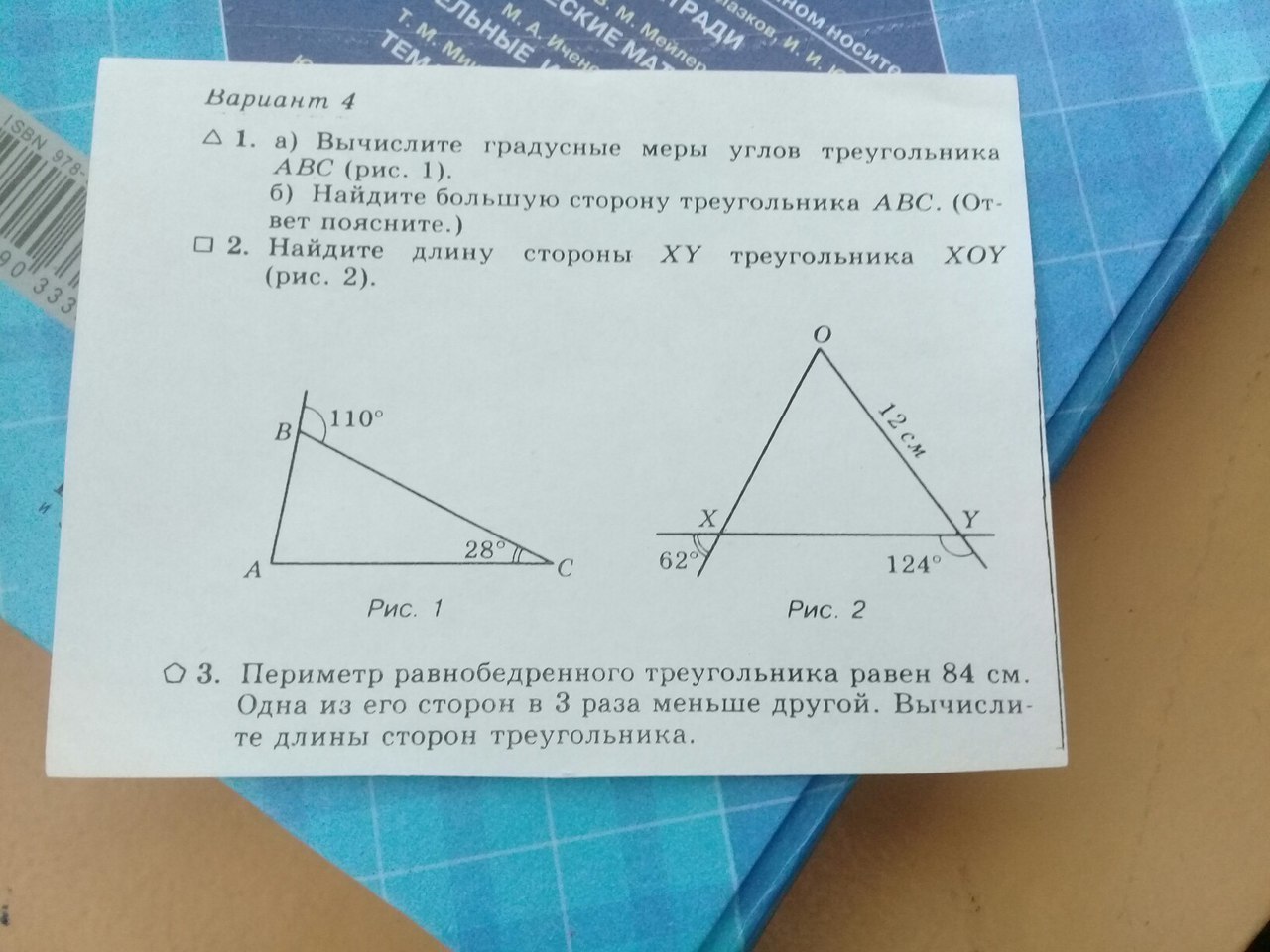
Великий французский ученый XVII в. Блез Паскаль (1623—1662) еще в детстве любил изучать геометрические фигуры, открывать их свойства, измерять углы транспортиром.
Юный исследователь заметил, что у любого треугольника сумма углов одна и та Ж6 180°. «Как же это объяснить?» — думал Паскаль. Тогда он отрезал у треугольника два уголка и приложил их к третьему (рис. 219). Получился развернутый угол, который, как известно, равен 180°. Это было его первое собственное открытие! Дальнейшая судьба мальчика была предопределена.
Теорема. Сумма углов треугольника равна 180°.
Дано: 
Доказать: 
Доказательство:
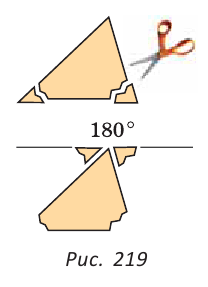
Через вершину В треугольника ABC проведем прямую КМ, параллельную стороне АС. Тогда 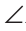
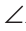
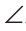
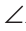





Следствия.
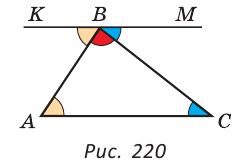
1. Каждый угол равностороннего треугольника равен 60°. (рис. 221).
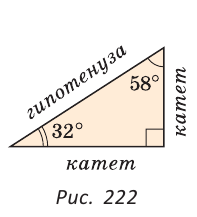
2. Сумма острых углов прямоугольного треугольника равна 90° (рис. 222).
В прямоугольном треугольнике стороны, заключающие прямой угол, называются катетами, сторона, противолежащая прямому углу, — гипотенузой (см. рис. 222).
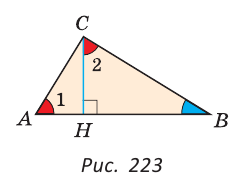
Проведем в прямоугольном треугольнике ABC высоту СН к гипотенузе АВ (рис. 223). Так как в треугольнике ABC угол 1 дополняет угол В до 90°, а в треугольнике СНВ угол 2 также дополняет угол В до 90°, то
Доказано свойство: «Угол между высотой прямоугольного треугольника, проведенной к гипотенузе, и катетом равен углу между другим катетом и гипотенузой».
Пример:
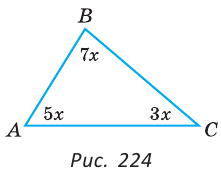
В треугольнике ABC градусные меры углов А, В и С относятся соответственно как 5:7:3. Найти углы треугольника (рис. 224).
Решение:
Пусть 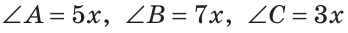
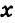
Так как сумма углов треугольника равна 180°, то
Тогда
Ответ:
Пример:
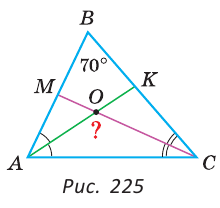
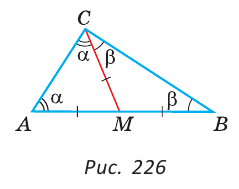
В треугольнике ABC (рис. 225) угол В равен 70°, АК и СМ — биссектрисы, О — точка их пересечения. Найти угол АОС между биссектрисами.
Решение:
Сумма углов А и С треугольника ABC равна 180° — 70° = 110°. Так как биссектриса делит угол пополам, то
Из треугольника АОС находим:
Замечание. Если 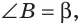
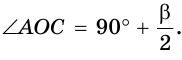
Пример:
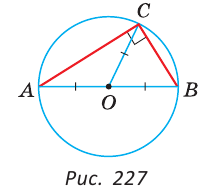
Доказать, что если медиана треугольника равна половине стороны, к которой она проведена, то данный треугольник — прямоугольный.
Доказательство:
Пусть СМ — медиана, 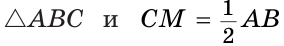
Докажем, что
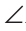























Замечание. Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным. На рисунке 227 это угол АСВ. Из задачи 3 следует свойство: «Вписанный угол, опирающийся на диаметр, — прямой».
Пример:
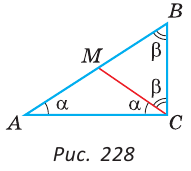
Доказать, что в прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы.
Доказательство:
Пусть в треугольнике ABC (рис. 228) 




Проведем отрезок СМ так, что










| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Внешний угол треугольника
- Свойство точек биссектрисы угла
- Свойство катета прямоугольного треугольника, лежащего против угла в 30°
- Четырехугольник и его элементы
- Перпендикулярные прямые в геометрии
- Признаки равенства треугольников
- Признаки равенства прямоугольных треугольников
- Соотношения в прямоугольном треугольнике
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Что такое угол? Виды углов: прямой, острый, тупой, развернутый уголСкачать

Решение треугольников онлайн
С помощю этого онлайн калькулятора можно решить треугольники, т.е. найти неизвестные элементы (стороны, углы) треугольника. Теоретическую часть и численные примеры смотрите ниже.
Решение треугольников − это нахождение всех его элементов (трех сторон и трех углов) по трем известным элементам (сторонам и углам). В статье Треугольники. Признаки равенства треугольников рассматриваются условия, при которых два треугольника оказываются равными друг друга. Как следует из статьи, треугольник однозначно определяется тремя элементами. Это:
- Три стороны треугольника.
- Две стороны треугольника и угол между ними.
- Две стороны и угол противостоящий к одному из этих сторон треугольника.
- Одна сторона и любые два угла.
Заметим, что если у треугольника известны два угла, то легко найти третий угол, т.к. сумма всех углов треугольника равна 180°.
Видео:Угол. Градусная мера угла. 5 класс.Скачать

Решение треугольника по трем сторонам
Пусть известны три стороны треугольника a, b, c (Рис.1). Найдем 
 |
 |
 |
 | (1) |
 | (2) |
Из (1) и (2) находим cosA, cosB и углы A и B (используя калькулятор). Далее, угол C находим из выражения
 . . |
Пример 1. Известны стороны треугольника ABC: 

Решение. Из формул (1) и (2) находим:
  . . |
  . . |
 , ,  . . |
И, наконец, находим угол C:
  |
Видео:Угол. 7 класс.Скачать
Решение треугольника по двум сторонам и углу между ними
Пусть известны стороны треугольника a и b и угол между ними C (Рис.2). Найдем сторону c и углы A и B.
 |
Найдем сторону c используя теорему косинусов:
 . . |
 . . |
Далее, из формулы
 . . |
 . . | (3) |
Далее из (3) с помощью калькулятора находим угол A.
Поскольку уже нам известны два угла то находим третий:
 . . |
Пример 2. Известны две стороны треугольника ABC: 

Решение. Иcпользуя теорму косинусов найдем сторону c:
 , , |
   . . |
Из формулы (3) найдем cosA:
  |
 . . |
Поскольку уже нам известны два угла то находим третий:
  . . |
Видео:Задача на определение градусной мерыСкачать

Решение треугольника по стороне и любым двум углам
Пусть известна сторона треугольника a и углы A и B (Рис.4). Найдем стороны b и c и угол C.
 |
Так как, уже известны два угла, то можно найти третий:
 . . |
Далее, для находждения сторон b и c воспользуемся тероемой синусов:
 , ,  . . |
 , ,  . . |
Пример 3. Известна одна сторона треугольника ABC: 

Решение. Поскольку известны два угла, то легко можно найти третий угол С:
  |
Найдем сторону b. Из теоремы синусов имеем:
 |
 |
Найдем сторону с. Из теоремы синусов имеем:
🔍 Видео
Углы треугольника относятся как 2:3:4. Найдите их градусные мерыСкачать

Радианная Мера Угла - Как Переводить Градусы в Радианы // Урок Алгебры 10 классСкачать

Измерение угла с помощью транспортираСкачать

Радианная мера угла. 9 класс.Скачать

7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать