Если четырехугольник описан около окружности то существует точка равноудаленная от

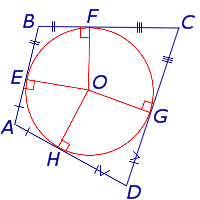
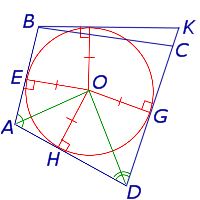
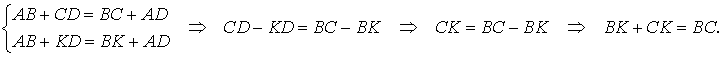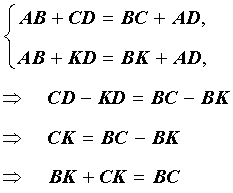Определение 1 . Окружностью, вписанной в четырёхугольник, называют окружность, которая касается касается каждой из сторон четырёхугольника (рис.1). В этом случае четырёхугольник называют четырёхугольником, описанным около окружности или описанным четырёхугольником .

Замечание . В настоящем разделе мы рассматриваем только выпуклые четырёхугольники.

Теорема 1 . Если четырёхугольник описан около окружности, то суммы длин его противоположных сторон равны.

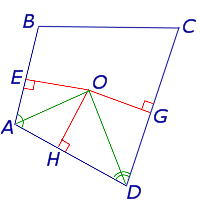
Доказательство . Рассмотрим четырёхугольник ABCD , описанный около окружности, и обозначим буквами E, F, G, H – точки касания сторон четырёхугольника с окружностью (рис.2).

AH = AE, BF = BE, CF = CG, DH = DG,

Складывая эти равенства, получим:

AH + BF + CF + DH =
= AD + BC,
AE + BE + CG + DG =
= AB + CD,

то справедливо равенство

что и требовалось доказать.

Теорема 2 (обратная теорема к теореме 1) . Если у четырёхугольника суммы длин противоположных сторон равны, то в этот четырёхугольник можно вписать окружность.

Доказательство . Рассмотрим четырёхугольник ABCD , длины сторон которого удовлетворяют равенству

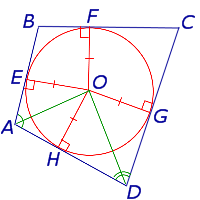
и проведём биссектрисы углов BAD и CDA . Обозначим точку пересечения этих биссектрис буквой O , и опустим из точки O перпендикуляры OH, OE и OG на стороны AD, AB и CD соответственно (рис.3).

Следовательно, справедливы равенства

из которых вытекает, что точки H, E и G лежат на окружности с центром в точке O и радиусом OH , касающейся сторон четырёхугольника AD, AB и CD в точках H, E и G соответственно. При этом возможны два случая:

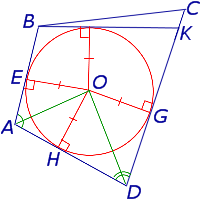
Окружность касается касается стороны BC (рис.4).

В этом случае четырёхугольник ABCD описан около окружности, и теорема доказана.

Окружность не касается стороны BC .

В этом случае касательная, проведенная к окружности из точки B , пересекает прямую DC в точке K , и возможны два случая:

Точка K лежит между точками C и D (рис.5)

Рассмотрим случай 2а и приведём его к противоречию. В этом случае в силу того, что четырёхугольник ABKD является описанным, а также по условию теоремы справедливы равенства:

Последнее равенство утверждает, что в треугольнике BKC сумма двух сторон равна третьей стороне, что противоречит неравенству треугольника неравенству треугольника неравенству треугольника . Полученное противоречие доказывает, что случай 2а невозможен.

Совершенно аналогичные рассуждения позволяют заключить, что случай 2b также невозможен.

Итак, возможен и реализуется лишь случай 1.

Из доказательства теоремы 2 непосредственно вытекает

Теорема 3 . Биссектрисы всех внутренних углов описанного четырёхугольника пересекаются в одной точке – центре вписанной окружности.

В следующей таблице приводятся примеры четырёхугольников, в которые можно вписать окружность. Доказательства утверждений непосредственно вытекают из теорем 1 и 2 и предоставляются читателю в качестве несложных упражнений.

Примеры описанных четырёхугольников

Фигура	Рисунок	Утверждение
Ромб		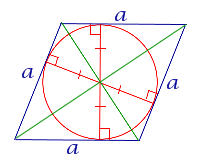В любой ромб можно вписать окружность
Квадрат		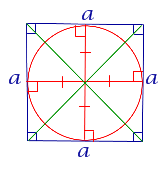В любой квадрат можно вписать окружность
Прямоугольник		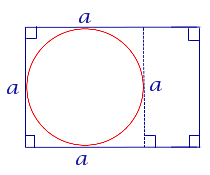В прямоугольник можно вписать окружность тогда и только тогда, когда он является квадратом
Параллелограмм		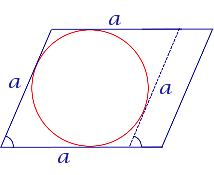В параллелограмм можно вписать окружность тогда и только тогда, когда он является ромбом
Дельтоид		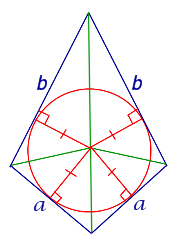В любой дельтоид можно вписать окружность
Трапеция		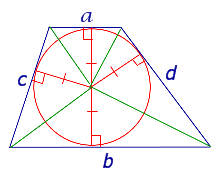В трапецию можно вписать окружность тогда и только тогда, когда у трапеции сумма длин боковых сторон рана сумме длин оснований

Ромб

Квадрат

В любой квадрат можно вписать окружность

Прямоугольник

В прямоугольник можно вписать окружность тогда и только тогда, когда он является квадратом

Параллелограмм

В параллелограмм можно вписать окружность тогда и только тогда, когда он является ромбом

Дельтоид

Трапеция

В трапецию можно вписать окружность тогда и только тогда, когда у трапеции сумма длин боковых сторон рана сумме длин оснований

Многоугольник. Свойства четырехугольников описанных около окружности.

Если все стороны какого-нибудь многоугольника (MNPQ) касаются окружности, то говорят, что этот многоугольник описан около окружности, или что окружность вписана в него.

Теорема.

В описанном выпуклом четырехугольнике суммы противоположных сторон равны.

Пусть ABCD будет описанный выпуклый четырехугольник, т.е. стороны его касаются окружности. Требуется доказать, что AB + CD = BC + AD.

Обратная теорема.

Если в выпуклом четырехугольнике равны суммы противоположных сторон, то в него можно вписать окружность.

Требуется доказать, что в него можно вписать окружность.

Пусть ABCD такой выпуклый четырехугольник, в котором: AB + CD = AD + BC.

Описанная окружность

Окружность описанная около многоугольника — это окружность, на которой лежат все вершины многоугольника. Вписанный в окружность многоугольник — это многоугольник, все вершины которого лежат на окружности. На рисунке 1 четырехугольник АВСD вписан в окружность с центром О, а четырехугольник АЕСD не является вписанным в эту окружность, так как вершина Е не лежит на окружности.

Теорема

Около любого треугольника можно описать окружность.

Доказательство

Дано: произвольный АВС.

Доказать: около АВС можно описать окружность.

Доказательство:

1. Проведем серединные перпендикуляры к сторонам АВС, которые пересекутся в точке О (по свойству серединных перпендикуляров треугольника). Соединим точку О с точками А, В и С (Рис. 2).

Точка О равноудалена от вершин АВС (по теореме о серединном перпендикуляре), поэтому ОА = ОВ = ОС. Следовательно, окружность с центром О радиуса ОА проходит через все три вершины треугольника, значит, является описанной около АВС. Теорема доказана.

Замечание 1

Около треугольника можно описать только одну окружность.

Доказательство

Предположим, что около треугольника можно описать две окружности. Тогда центр каждой из них равноудален от его вершин и поэтому совпадает с точкой О пересечения серединных перпендикуляров к сторонам треугольника, а радиус равен расстоянию от точки О до вершин треугольника. Следовательно, эти окружности совпадают, т.е. около треугольника можно описать только одну окружность. Что и требовалось доказать.

Замечание 2

Около четырехугольника не всегда можно описать окружность.

Доказательство

Рассмотрим, например, ромб, не являющийся квадратом. Такой ромб можно «поместить» в окружность так, что две его вершины будут лежать на этой окружности (Рис. 3), но нельзя «поместить» ромб в окружность так, чтобы все его вершины лежали на окружности, т.к. диаметр окружности, равный одной из диагоналей ромба, будет больше (меньше) второй диагонали, т.е. нельзя описать окружность. Что и требовалось доказать.

Если же около четырехугольника можно описать окружность, то его углы обладают следующим замечательным свойством:

В любом вписанном четырехугольнике сумма противоположных углов равна 180 0 .

Доказательство

Рассмотрим четырехугольник АВСD, вписанный в окружность (Рис. 4).

Углы В и D — вписанные, тогда по теореме о вписанном угле: В = АDС, D = АВС, откуда следует В + D = АDС + АВС = (АDС + АВС). Дуги АDС и АВС вместе составляют окружность, градусная мера которой равна 360 0 , т.е. АDС + АВС = 360 0 , тогда В + D = 360 0 = 180 0 . Что и требовалось доказать.

Верно и обратное утверждение:

Если сумма противоположных углов четырехугольника равна 180 0 , то около него можно описать окружность.

Доказательство

Дано: четырехугольник АВСD, BАD + BСD = 180 0 .

Доказать: около АВСD можно описать окружность.

Доказательство:

Проведем окружность через три вершины четырехугольника: А, В и D (Рис. 5), — и докажем, что она проходит также через вершину С, т.е. является описанной около четырехугольника АВСD.

Предположим, что это не так. Тогда вершина С лежит либо внутри круга, либо вне его.

Рассмотрим первый случай, когда точка С лежит внутри круга (Рис. 6).

ВСD — внешний угол СFD, следовательно, BСD = ВFD + FDE. (1)

Углы ВFD и FDE — вписанные. По теореме о вписанном угле ВFD = ВАD и FDE = ЕF, тогда, подставляя данные равенства в (1), получим: BСD = ВАD + ЕF = (ВАD + ЕF), следовательно, ВСDВАD.

BАD — вписанный, тогда по теореме о вписанном угле BАD = ВЕD, тогда BАD + BСD(ВЕD + ВАD).

Дуги ВЕD и ВАD вместе составляют окружность, градусная мера которой равна 360 0 , т.е. ВЕD + ВАD = 360 0 , тогда BАD + BСD360 0 = 180 0 .

Итак, мы получили, что BАD + BСD180 0 . Но это противоречит условию BАD + BСD =180 0 , и, значит, наше предположение ошибочно, т.е. точка С лежит на окружности, значит, около четырехугольника АВСD можно описать окружность.

Рассмотрим второй случай, когда точка С лежит вне круга (Рис. 7).

По теореме о сумме углов треугольника в ВСF: С + В + F = 180 0 , откуда С = 180 0 — ( В + F). (2)

В — вписанный, тогда по теореме о вписанном угле В = ЕF. (3)

F и ВFD — смежные, поэтому F + ВFD = 180 0 , откуда F = 180 0 — ВFD = 180 0 — ВАD. (4)

Подставим (3) и (4) в (2), получим:

С = 180 0 — (ЕF + 180 0 — ВАD) = 180 0 — ЕF — 180 0 + ВАD = (ВАD — ЕF), следовательно, СВАD.

А — вписанный, тогда по теореме о вписанном угле А = ВЕD, тогда А + С(ВЕD + ВАD). Но это противоречит условию А + С =180 0 , и, значит, наше предположение ошибочно, т.е. точка С лежит на окружности, значит, около четырехугольника АВСD можно описать окружность. Что и требовалось доказать.

Примечание:

Окружность всегда можно описать:

Поделись с друзьями в социальных сетях:

🎦 Видео