Scilab работа с векторами (8 видео) | Курс школьной геометрии

IT Novella

Данный пост является продолжением поста Основы работы в Scilab.

Векторы и матрицы представляют собой одномерный и двумерный массивы.

Значение нижней границы индексации элементов массива в Scilab по умолчанию равно единице.

Одномерный массив (вектор-строку) можно задать с помощью команды

где X -название массива, a и b — значения первого и последнего элементов массива, h — шаг, с которым изменяются элементы массива. Возможна запись вида

В этом случае шаг автоматически принимается равным единице. Пример. Задать вектор-строку X с элементами -2,-1,0,1,2.

Пример. Задать вектор-строку X с элементами -2, -1.5, -1, -0.5, 0, 0.5, 1, 1.5, 2.

Другой способ определить вектор — перечислить все его элементы. В этом случае нужно выполнить команду

где X -имя вектора, x1,x2. xn — элементы массива. Пример. Задать вектор-строку X с элементами -5, 0.5, -7, 25.

Для того, чтобы задать вектор-столбец, необходимо перечислить элементы через точку с запятой. Пример. Задать вектор-столбец X с элементами -5, 0.5, -7, 25.

Другой способ задать вектор-столбец — использовать транспонирование матриц. Операция транспонирования задается с помощью знака ‘. Пример.

Для доступа к элементам вектора нужно указать название вектора и в круглых скобках номер элемента. Пример.

Для того, чтобы задать матрицу с элементами xij, нужно выполнить команду вида

Для доступа к элементам нужно указать название матрицы и в круглых скобках номер элемента. Пример.

Матрицы можно формировать на основе имеющихся

С помощью знака «:» можно выполнять различные операции с матрицами Пример.

При работе с матрицами в пакете Scilab можно использовать следующие операции: 1. + — сложение; Пример.

Если к заданной матрице применить некоторую функцию, то элементы матрицы будут преобразованы в соответствии с этой функцией. Пример.

При работе с матрицами можно использовать встроенные функции. Рассмотрим некоторые из них. Функция length(X) возвращает количество элементов матрицы X. Пример.

Функция size(X) возвращает вектор, содержащий количество строк и столбцов матрицы X. Пример.

Функция max(X) возвращает максимальный элемент матрицы X.

Функция min(X) возвращает минимальный элемент матрицы X.

Функция sum(X) возвращает сумму элементов матрицы X.

Функция prod(X) возвращает произведение элементов матрицы X.

Функция det(X) возвращает определитель матрицы X.

Функция inv(X) возвращает матрицу, обратную к X.

Содержание

Массивы в Scilab
2.1 Одномерные массивы (столбцы и строки)
2.2 Двумерные массивы (матрицы)
2.3 Специальные функции для векторов и матриц
Лабораторная работа №2 Массивы и матрицы в Scilab
🎦 Видео

Видео:Работа с матрицами в ScilabСкачать

Массивы в Scilab

Scilab — матрично-ориентированный язык. Под массивами в данном мат. пакете понимаются конструкции, используемые в линейной алгебре: матрицы, векторы-строки и векторы-столбцы.

Под массивами в данном случае понимаются конструкции, используемые в линейной алгебре: матрицы, векторы-строки и векторы-столбцы.

Важно! Нумерация элементов массива в Scilab начинается с 1.

Видео:Практическая часть лабораторной работы. Компьютерное моделирование в приложении Хсоs, Scilab.Скачать

2.1 Одномерные массивы (столбцы и строки)

Задать одномерный массив в Scilab можно следующим образом:

Здесь MAS – имя переменной, куда будет записан сформированный массив, v1 – значение первого элемента массива, vmax – значение последнего элемента массива, d – шаг, с которым будет происходить формирование элементов.

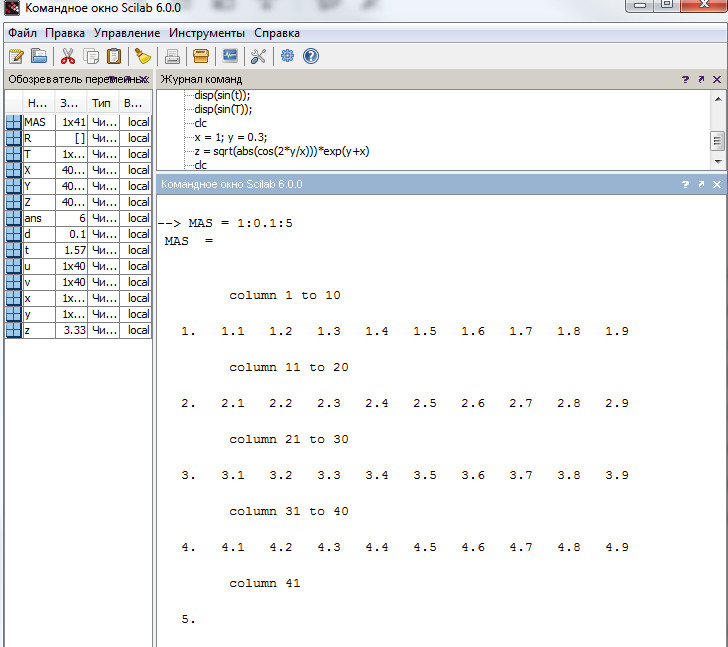
Например, сформируем массив с элементами от 1 до 5 с шагом 0.1 (листинг 4).

Листинг 4. Задание одномерного массива из 41 элемента.

Сформировать одномерный массив можно и непосредственным перечислением всех его элементов через запятую или пробел:

MAS = [v1, v2, … , vmax] или MAS = [v1 v2 … vmax]

Отметим, что данные способы формируют вектор-строку в которую записаны всего vmax элементов.

Для поэлементного задания вектор-столбца нужно разделять элементы массива точкой с запятой «;», то есть, воспользоваться записью:

Обращение к элементу массива происходит через указание номера элемента в круглых скобках у имени массива. Чтобы выбрать 2-й элемент одномерного массива MAS, необходимо ввести команду:

Создадим вектор-строку row из 11 элементов, начиная с 0 с шагом 0.1. Это делается следующим образом:

Сейчас row — это вектор-строка вида ( (0; 0.1; 0.2; 0.3; 0.4; 0.5; 0.6 ;0.7; 0.8 ;0.9; 1) )

Получим 5-й эелемент вектор-строки row и выведем этот элемент:

x=row(5); // присвоили переменной х значение, записанное в 5-й столбец строки row
disp(x); // выведет 0.4

Видео:Массивы и матрицы SCILABСкачать

2.2 Двумерные массивы (матрицы)

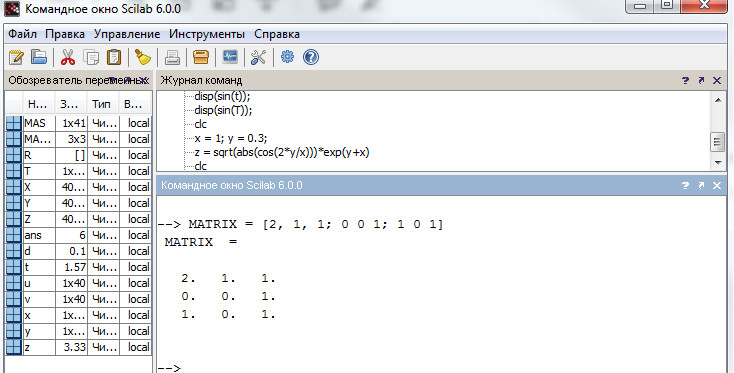
Двумерные массивы, или матрицы, также задаются при помощи квадратных скобок, при этом строки матрицы разделяются точкой с запятой «;», а столбцы — запятой или пробелом (листинг 5).

Листинг 5. Задание матрицы поэлементно.

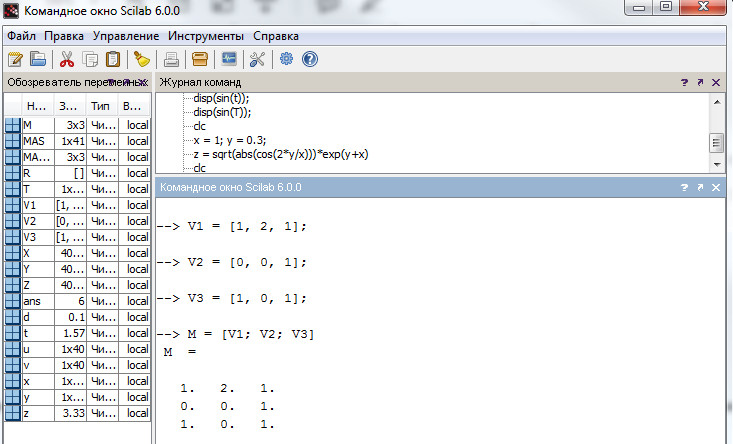
Кроме того, матрица может быть сформирована из векторов-строк или векторов-столбцов, заданных ранее (листинг 6).

Листинг 6. Задание матрицы из сформированных строк V1, V2, V3.

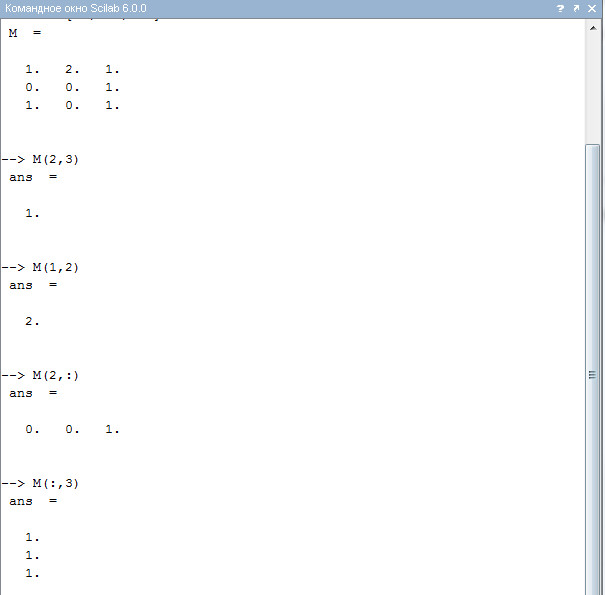
Обращение к элементу матрицы происходит через указание номера строки и столбца в круглых скобках у имени матрицы. Например, чтобы выбрать 3-й элемент из второй строки матрицы M, необходимо ввести команду:

M(2,3) // элемент из 2-й строки 3-го столбца 1

Отметим, что значения элементов матрицы можно использовать, присвоив их значения некоторым переменным, например:

Важную роль в работе с матрицами играет знак двоеточия «:». Указывая его, можно получить целую строку или целый столбец. Например, чтобы выбрать третий столбец матрицы, нужно записать M(:,3). А чтобы получить все элементы второй строки, нужно записать M(2,:). Смотри (листинг 7).

Листинг 7. Выбор элементов m23, m12 матрицы М; 2-й строки и 3-го столбца матрицы М.

Видео:Scilab Лабараторная 1.1Скачать

2.3 Специальные функции для векторов и матриц

В Scilab предусмотрены специальные функции для работы с матрицами. Эти функции обеспечивают быстрое создание распространенных типов матриц. Такими функциями являются следующие:

Кроме того, в мат. пакете есть ряд функций, полезных для решения задач линейной алгебры и устойчивости систем линейных дифференциальных уравнений.

det(M) – вычисление определителя квадратной матрицы;

spec(M) – находит собственные числа матрицы М;

Отметим, что для работы с матрицами и векторами предусмотрены стандартные операции сложения «+», матричного умножения и умножения на число «*», вычитания «-», возведения в степень «^», деления « / ».

Отдельно стоит выделить операции транспонирования «’» и поэлементного умножения « .* ».

Результаты операций с матрицами продемонстрированы ниже на Листинге 8.

Листинг 8. Операции матричного умножения, поэлементного умножения и транспонирования.

Видео:Решение уравнений в ScilabСкачать

Лабораторная работа №2 Массивы и матрицы в Scilab

Лабораторная работа №2

Массивы и матрицы в Scilab.

1. Научиться задавать матрицы.

2. Изучить действия с матрицами и векторами.

3. Изучить специальные матричные функции.

Ввод и формирование массивов и матриц

Задать одномерный массив в Scilab можно следующим образом:

где name — имя переменной, в которую будет записан сформированный массив, Xn — значение первого элемента массива, Xk — значение последнего элемента массива, dX — шаг, с помощью которого формируется каждый следующий элемент массива, т. е. значение второго элемента составит Xn+dX, третьего Xn+ dX+dX и так далее до Xk.

Если параметр dX в конструкции отсутствует, это означает, что по умолчанию он принимает значение, равное единице, т. е. каждый следующий элемент массива равен значению предыдущего плюс один:

Переменную, заданную как массив, можно использовать в арифметических выражениях и в качестве аргумента математических функций. Результатом работы таких операторов являются массивы:

Примеры работы с массивами

-3.5000 -2.0000 -0.5000 1.0000 2.5000 4.0000

-0.9840 -0.8415 -0.2474 0.4794 0.9490 0.9093

3.1416 3.6416 4.1416 4.6416 5.1416 5.6416

Еще один способ задания векторов и матриц в Scilab — это их поэлементный

Так, для определения вектора-строки следует ввести имя массива, а затем

после знака присваивания, в квадратных скобках через пробел или запятую,

перечислить элементы массива:

name=[x1 x2 . xn] или name=[x1, x2, . xn]

Пример ввода вектора-строки:

1.1000 2.3000 -0.1000 5.8800

Элементы вектора-столбца вводятся через точку с запятой:

Пример ввода вектора-столбца:

Обратиться к элементу вектора можно, указав имя массива и порядковый

номер элемента в круглых скобках:

Ввод элементов матрицы также осуществляется в квадратных скобках, при этом элементы строки отделяются друг от друга пробелом или запятой, а строки разделяются между собой точкой с запятой:

name=[x11, x12, . x1n; x21, x22, . x2n; . ;

Обратиться к элементу матрицы можно, указав после имени матрицы, в круглых скобках через запятую, номер строки и номер столбца на пересечении которых элемент расположен:

Далее приведен пример задания матрицы и обращение к ее элементам:

—> A=[1 2 3;4 5 6;7 8 9]

Кроме того, матрицы и векторы можно формировать, составляя их из ранее заданных матриц и векторов:

—> v1=[1 2 3]; v2=[4 5 6]; v3=[7 8 9];

—> //Горизонтальная конкатенация векторов-строк:

V = 1 2 3 4 5 6 7 8 9

—>//Вертикальная конкатенация векторов-строк,

—>//Горизонтальная конкатенация матриц:

1 2 3 1 2 3 1 2 3

4 5 6 4 5 6 4 5 6

7 8 9 7 8 9 7 8 9

—>//Вертикальная конкатенация матриц:

Важную роль при работе с матрицами играет знак двоеточия «:». Указывая

его вместо индекса при обращении к массиву, можно получать доступ к группам

его элементов. Например:

—>//Пусть задана матрица А

—> A=[5 7 6 5; 7 10 8 7;6 8 10 9;5 7 9 10]

—> //Выделить из матрицы А второй столбец

—> //Выделить из матрицы А третью строку

—> //Выделить из матрицы А подматрицу М

—> //Удалить из матрицы А второй столбец

—> //Удалить из матрицы А третью строку

—> //Представить матрицу М в виде вектора-столбца

—> //Выделить из вектора v элементы со второго по четвертый

32 Глава 3. Массивы и матрицы в Scilab. Решение задач линейной алгебры

—> //Удалить из массива b второй элемент

Действия над матрицами

Для работы с матрицами и векторами в Scilab предусмотрены следующие

* — умножение на число;

€ — возведение в степень;

.* — поэлементное умножение матриц;

.€ — поэлементное возведение в степень;

. — поэлементное левое деление;

./ — поэлементное правое деление.

Пример действий над матрицами:

—>A=[1 2 0;-1 3 1;4 -2 5];

—>B=[-1 0 1;2 1 1;3 -1 -1];

—>//Вычислить (AT+B)2 — 2A(0.5BT-A)

—> //Решить матричные уравнения А•Х=В и Х•A=B.

—>//Решение матричного уравнения AX=B:

—>//Решение матричного уравнения XA=B:

Кроме того, если к некоторому заданному вектору или матрице применить

математическую функцию, то результатом будет новый вектор или матрица той

же размерности, но элементы будут преобразованы в соответствии с заданной

0.0998 -0.8085 0.0016 0 -0.8415

Специальные матричные функции

Для работы с матрицами и векторами в Scilab существуют специальные функции. Рассмотрим наиболее часто используемые из них.

Функции определения матриц:

• matrix(A [,n, m]) — преобразует матрицу A в матрицу другого размера;

• ones(m, n) — создает матрицу единиц из m строк и n столбцов;

—>ones(1,3) //Формируется вектор-строка

—>ones(2,2) //Формируется квадратная матрица

—>X=ones(m, n) //Формируется матрица размерности m на n

—>//Формируется матрица Y, состоящая из единиц,

—>//той же размерности, что и матрица M

• zeros(m, n) — создает нулевую матрицу1 из m строк и n столбцов;

• eye(m, n) — формирует единичную матрицу3 из m строк и n столбцов;

—>//Формируется единичная матрица E

—>//той же размерности, что и матрица M

—>//Функцию можно использовать без параметров eye().

—>//В этом случае задается матрица с неопределенными

—>//размерами, которые будут определены после суммирования

—>//с другой, определенной ранее, матрицей.

• rand(n1,n2. nn[,fl]) — формирует многомерную матрицу случайных

чисел. Необязательный параметр p — это символьная переменная, с помощью которой можно задать тип распределения случайной величины (’uniform’ — равномерное, ’normal’ — гауссовское); rand(m, n) — формирует матрицу m на n случайных чисел; rand(M) — формирует матрицу случайных чисел, размер которой совпадает с размером матрицы М; результат функции rand() — случайное скалярное число;

—>rand(2,2)//Матрица 2 на 2 случайных чисел

—> R=rand(2,2,2)//Многомерный массив случайных чисел

• sparse([i1 j1;i2 j2;. ;in jn],[n1,n2. nn]) — формирует разреженную матрицу. Для создания матрицы такого типа необходимо указать индексы ее ненулевых элементов — [i1 j1,i2 j2. in jn], и их значения — [n1,n2. nn]. Индексы одного элемента отделяются друг от друга либо пробелом, либо запятой, а пары индексов — соответственно точкой с запятой, значения элементов разделяются запятыми. При попытке просмотреть матрицу подобного типа пользователю будет предоставлено сообщение о ее размерности, а также значения ненулевых элементов и их местоположение в матрице;

• full(M) — вывод разреженной матрицы М в виде таблицы;

• hypermat(D[,V]) — создание многомерной матрицы с размерностью, заданной вектором D и значениями элементов, хранящихся в векторе V (использование параметра V необязательно);

• diag(V[,k]) — возвращает квадратную матрицу с элементами V на главной

или на k-й диагонали; функция diag(A[,k]), где A — ранее определенная

матрица, в качестве результата выдаст вектор-столбец, содержащий элементы главной или k-ой диагонали матрицы А;

• cat(n, A, B, [C, . ]) — объединяет матрицы А и В или все входящие

матрицы, при n=1 по строкам, при n=2 по столбцам; то же что [A; B] или

• tril(A[,k]) — формирует из матрицы А нижнюю треугольную матрицу1, начиная с главной или с k-й диагонали;

• triu(A[,k]) — формирует из матрицы А верхнюю треугольную матрицу1 , начиная с главной или с k-й диагонали;

• sort(X) — выполняет упорядочивание массива X; если X — матрица, сортировка выполняется по столбцам;

• size(V[,fl]) — определяет размер массива V; если V — двумерный массив, то size(V,1) или size(V,’r’) определяют число строк матрицы V, а size(V,2) или size(V,’c’) — число столбцов;

• length(X) — определяет количество элементов массива X; если X — вектор,

его длину; если X — матрица, вычисляет общее число ее элементов;

• sum(X[,fl]) — вычисляет сумму элементов массива X, имеет необязательный параметр fl. Если параметр fl отсутствует, то функция sum(X) возвращает скалярное значение, равное сумме элементов массива. Если fl=’r’

или fl=1, что то же самое, то функция вернет строку, равную поэлементной

сумме столбцов матрицы X. Если fl=’с’ или fl=2, то результатом работы

функции будет вектор-столбец, каждый элемент которого равен сумме элементов строк матрицы X. Частный случай применения функции sum — это

вычисление скалярного произведения векторов;

• prod(X[,fl]) — вычисляет произведение элементов массива X, работает

аналогично функции sum;

• max(M[,fl]) — вычисляет наибольший элемент в массиве M, имеет необя-

зательный параметр fl. Если параметр fl отсутствует, то функция max(M)

возвращает максимальный элемент массива M; если fl=’r’, то функция

вернет строку максимальных элементов столбцов матрицы M; если fl=’с’,

то результатом работы функции будет вектор-столбец, каждый элемент ко-

торого равен максимальному элементу соответствующих строк матрицы M.

Функция [x, nom]=max(M[,fl]) вернет значение максимального элемента

x и его номер в массиве nom;

• min(M[,fl]) — вычисляет наименьший элемент в массиве M, работает ана-

логично функции max;

• mean(M[,fl]) — вычисляет среднее значение массива M; если M двумерный

массив, то mean(M,1) или mean(M,’r’) определяют среднее значение строк

матрицы M, а mean(M,2) или mean(M,’c’) — среднее значение столбцов;

• mean(M[,fl]) — вычисляет среднее значение массива M; если M двумерный

массив, то mean(M,1) или mean(M,’r’) определяют среднее значение строк

матрицы M, а mean(M,2) или mean(M,’c’) — среднее значение столбцов;

• det(M) — вычисляет определитель квадратной матрицы М;

• rank(M[,tol]) — вычисление ранга матрицы M с точностью tol.

• norm(M[,fl]) — вычисление нормы квадратной матрицы М; тип нормы

определяется необязательной строковой переменной fl, по умолчанию

fl=2. Функции norm(M) и norm(M,2) эквивалентны и вычисляют вторую

норму матрицы М. Первая норма3 определяется функцией norm(M,1).

Функции norm(M,’inf’) и norm(M,’fro’) вычисляют соответственно бес-

конечную4 и евклидову нормы. Если V — вектор, то результатом работы функции norm(V,1) будет сумма модулей всех элементов вектора V. С по-

мощью функции norm(V,2) можно вычислить модуль вектора V. Значение

norm(V,’inf’) равно модулю максимального элемента вектора по модулю;

• сond(M) — вычисляет число обусловленности1 матрицы М по второй норме;

• spec(M) — вычисляет собственные значения и собственные векторы1 квад-

ратной матрицы M.

• inv(A) — вычисляет матрицу, обратную2 к A;

• pinv(A[,tol]) — вычисляет псевдообратную матрицу для матрицы A с

точностью tol (необязательный параметр);

• linsolve(A, b) — решает систему линейных алгебраических уравнений вида A ·

• rref(A) — осуществляет приведение матрицы A к треугольной форме, ис-

пользуя метод исключения Гаусса;

• lu(М) — выполняет треугольное разложение матрицы M;

• qr(М) — выполняет разложение матрицы М на ортогональную и верхнюю

• svd(М) — выполняет сингулярное разложение1 размером nЧm; результатом

работы функции может быть либо сингулярное разложение, либо вектор,

содержащий сингулярные значения матрицы;

• kernel(М[,tol[,fl]]) — определение ядра матрицы2 М, параметры tol и

fl являются необязательными. Первый задает точность вычислений, второй — используемый при вычислении алгоритм и принимает значения ’qr’

У каждого индивидуальный вариант, уточняйте у преподавателя.