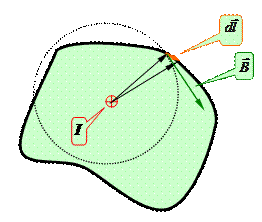
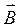
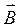
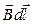
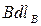
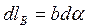
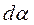
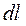
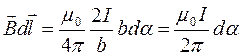
Ротор вектора магнитного поля (3 видео) | Курс школьной геометрии

Ротор магнитного поля

Циркуляция вектора наиболее просто вычисляется в случае прямого тока. Рассмотрим замкнутый контур, лежащий в плоскости, перпендикулярной к току. В каждой точке контура направлен по касательной к окружности с центром в месте прохождения тока и проходящей через данную точку. В выражении для циркуляции заменим на . Учтем, что — угол, на который поворачивается радиальная прямая при перемещении вдоль контура на . Таким образом,

(18.43)

Тогда для циркуляции получаем

(18.44)

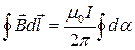
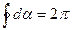
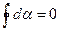
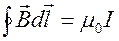
Если рассматриваемый контур охватывает ток, то при обходе по контуру радиальная прямая поворачивается в одном направлении и . Если же контур не охватывает тока, то . Поэтому можно записать:

(18.45)

где под I подразумевается ток, охватываемый контуром.

В выражении (18.45) ток рассматривается как алгебраическая величина: если направление обхода контура образует с направлением тока правовинтовую систему, то ток считают положительным, в противном случае — отрицательным.

Формула (18.45) получена для прямого тока. Но можно доказать, что онасправедлива и в общем случае, для тока произвольной формы.

Представим, что некоторый контур охватывает не один а несколько токов. Для каждого из них справедливо соотношение (18.45). В соответствии с принципом суперпозиции индукция результирующего поля равна векторной сумме полей каждого из этих токов. Поэтому циркуляция вектора индукции результирующего поля (18.46)

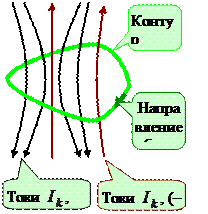
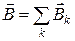
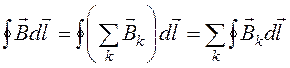
По формуле (18.45)

(18.47)

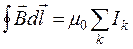
Важно помнить, что сумма в (18.47) является алгебраической.

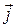
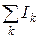
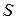
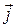
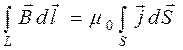
Возможны ситуации, когда токи распределены в пространстве с некоторой плотностью . Этом случае вместо в (18.47) следует взять ток, который протекает через некоторую поверхность , опирающуюся на контур L . При этом поверхность может быть произвольной, единственное требование – она должна опираться на контур L. Суммарный ток через такую поверхность равен потоку вектора через нее. Поэтому соотношение (18.47) можно представить в виде:

(18.48)

По теореме Стокса

. (18.49)

. (18.50)

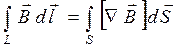
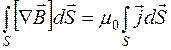
Поверхность интегрирования может быть произвольной (опирающуйся на контур L), поэтому должны быть равны подынтегральные выражения:

. (18.51)

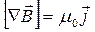
Формулы (18.48) и (18.51) отражают существенное отличие электрического и магнитного полей: циркуляция и ротор вектора напряженности электрического поля равны нулю. Это является следствием того, что электростатическое поле потенциально и может быть описано с помощью скалярного потенциала.

Магнитное поле не является потенциальным, его циркуляция не обязательно равна нулю, его нельзя описать с помощью скалярного потенциала. Такие поля называют вихревыми или соленоидальными.

Дата добавления: 2016-06-02 ; просмотров: 650 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Видео:Александр Чирцов: ротор, дивергенция и градиентСкачать

Дивергенция и ротор векторного поля

Электромагнитные поля и волны. Основные понятия и определения

ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ

Электрические заряды обусловливают электрические и магнитные явления, например, силовые взаимодействия между заряженными частицами и телами.

Взаимодействие между заряженными частицами или телами осуществляется через электромагнитное поле.

Электромагнитное поле определяется как особый вид материи, характеризующийся способностью распространяться в вакууме со скоростью, близкой к 3×10 8 м/с и оказывающий силовое воздействие на заряженные частицы.

Электромагнитное поле представляет собой единство двух своих составляющих – электрического и магнитного полей.

В каждой точке пространства, где имеет место электромагнитное поле, оно характеризуется величиной и направлением векторов:

Е– напряженности электрического поля;

D – электрического смещения (электрической индукции);

Н – напряженности магнитного поля;

В – магнитной индукции.

Векторы поля D и Н – это функции источников.

Вектор электрического смещения D, Кл/м 2 , равен

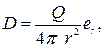
где e_r– орт, направленный вдоль радиус-вектора.

Вектор напряженности магнитного поля Н, А/м , характеризует связь электрического тока с собственным магнитным полем

где — орт в цилиндрической системе координат, у которой ось z совпадает с направлением тока.

Векторы Е и В являются силовыми характеристиками электромагнитного поля.

Эта сила является суперпозицией сил, создаваемых электрической и магнитной составляющими поля:

где – вектор скорости движения заряда.

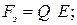Электромагнитные свойства среды

Электромагнитные взаимодействия между зарядами и полями зависят от свойств среды.

Макроскопические параметры среды в каждой точке поля связывают попарно векторы электромагнитного поля:

где J – плотность электрического тока,

s – удельная электрическая проводимость среды.

– абсолютная диэлектрическая проницаемость среды.

– абсолютная магнитная проницаемость.

Данные выражения верны только для изотропных сред.

Классификация сред

Все среды можно классифицировать в зависимости от выбранного признака, положенного в основание классификации. Различают следующие среды:

Дадим каждой среде определение.

Однородная среда — это среда, параметры которой не зависят от координат.

Неоднородная среда — это среда, параметры которой являются функциями координат.

Линейная среда — это среда, параметры которой не зависят от внешнего воздействующего поля, а материальные уравнения носят линейный характер.

Нелинейная среда — это среда, параметры которой зависят от внешнего воздействующего поля.

Изотропная среда — это среда, свойства которой не зависят от направления векторов поля и параметры которой являются скалярными величинами.

Анизотропная среда — это среда, свойства которой зависят от направления векторов поля и параметры среды являются тензорными величинами.

Дивергенция и ротор векторного поля

Дивергенцией или расхождением поля Д называется скаляр, определенный в каждой точке поля и являющийся объемной производной этого поля:

Вычисляется по формуле:

(в декартовых координатах).

Ротор (иначе ротация) поля D есть вектор, определенный в каждой точке поля и являющийся объемной производной этого поля, взятой с обратным знаком:

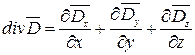
Формула для вычисления в декартовых координатах имеет следующее выражение

Видео:#8 Ротор/Дивергенция/ГрадиентСкачать

Ротор векторного поля и его физический смысл

В качестве еще одной важной меры направленности физического поля выступает характеристика, получившая название ротор или вихрь.

Ротор <вихрь)— это векторный дифференциальный оператор над векторным полем. Ротор поля F обозначается символом rot F, он определяется векторным произведением

где V — векторный дифференциальный оператор набла. Результат действия этого оператора на конкретное векторное поле F представляет собой новое векторное поле.

Физически поле ротора F, т.е. длина и направление вектора rot F в каждой точке пространства, характеризует в некотором смысле вращательную составляющую поля F соответственно в каждой точке. Или по-

другому показывает, насколько и в каком направлении закручено поле в каждой точке.

Математически ротор векторного поля F — есть вектор, проекция которого rot_nF на каждое направление п равна пределу отношения циркуляции векторного поля по замкнутому контуру L, являющемуся краем плоской площадки AS, перпендикулярной к этому направлению, к величине этой площадки, когда размеры площадки стремятся к нулю, а сама площадка стягивается в точку:

При этом направление обхода контура выбирается так, чтобы, если смотреть в направлении п, контур L обходился по часовой стрелке.

В трехмерной декартовой системе координат ротор вычисляется следующим образом:

где i,j и к- единичные орты (векторы) для осейх,у иz соответственно.

Для удобства представления можно условно представлять ротор в матричном виде как векторное произведение, формально представляющее векторное произведение как определитель:

Анализ основных свойств ротора позволяет сделать следующие выводы:

1) Дивергенция ротора векторного поля равна нулю:

т.е. поле не имеет источников. При этом верно и обратное: если поле F бездивергентно, оно есть поле ротора некоторого потенциального поля G:

2) Если поле F потенциально, то его ротор равен нулю в любой точке поля, т.е. поле F является безвихревым:

Верно и обратное: если поле безвихревое, то оно потенциально для некоторого скалярного поля (р.

В теории поля между циркуляцией векторного поля и его ротором установлена связь, доказанная теоремой Стокса, которая формулируется следующим образом: циркуляция вектора силы поля по замкнутому контуру, являющемуся границей некоторой поверхности, равна потоку ротора этого вектора через поверхность, ограниченную этой кривой, в направлении нормали.

В качестве примера рассмотрим векторное поле, силовые линии, которого линейно зависят от координат х и у. Вид этого поля, закрученного по часовой стрелке, представлен на рис. 2.6 а). Если поместить колесо с лопастями в любой области этого поля, то можно увидеть, что оно начнет вращаться по направлению часовой стрелки. Используя правило правой руки, можно установить, что поле ввинчивается в страницу. Для правой системы координат направление в страницу будет означать отрицательное направление по оси z. График ротора F представлен на рис. 2.6, б).

Рисунок 2.6 — Вихревое векторное поле и график его ротора

Через понятие ротор принято выражать одно из уравнений Максвелла, описывающее закон электромагнитной индукции Фарадея. Данный закон говорит, что ротор электрического поля равен скорости изменения магнитного поля, взятой с обратным знаком, а ротор напряженности магнитного поля равен сумме плотностей тока обычного и тока смещения.