Найдите точки минимума функции на окружности

Минимумом называют точку на функции, в которой значение функции меньше, чем в соседних точках.

Максимумом называют точку на функции, в которой значение функции больше, чем в соседних точках.

Также можно сказать, что в этих точках меняется направление движения функции: если функция перестает падать и начинает расти – это точка минимума, наоборот – максимума.

Минимумы и максимумы вместе именуют экстремумами функции.

Иными словами, все пять точек, выделенных на графике выше, являются экстремумами.

В точках экстремумов (т.е. максимумов и минимумов) производная равна нулю.

Благодаря этому найти эти точки не составляет проблем, даже если у вас нет графика функции.

Внимание! Когда пишут экстремумы или максимумы/минимумы имеют в виду значение функции т.е. (y). Когда пишут точки экстремумов или точки максимумов/минимумов имеют в виду иксы в которых достигаются максимумы/минимумы. Например, на рисунке выше, (-5) точка минимума (или точка экстремума), а (1) – минимум (или экстремум).

Видео:АЛГЕБРА С НУЛЯ — Точки Экстремума ФункцииСкачать

Как найти точки экстремумов функции по графику производной (7 задание ЕГЭ)?

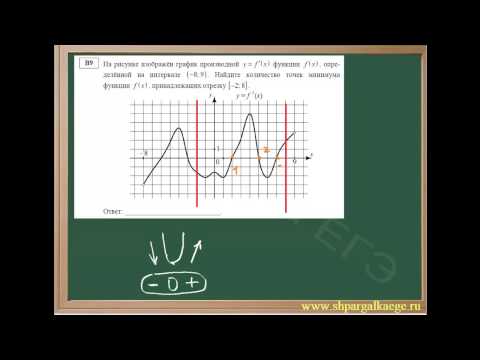
Давайте вместе найдем количество точек экстремума функции по графику производной на примере:

У нас дан график производная — значит ищем в каких точках на графике производная равна нулю. Очевидно, это точки (-13), (-11), (-9),(-7) и (3). Количество точек экстремума функции – (5).

Внимание! Если дан график производной функции, а нужно найти точки экстремумов функции, мы не считаем максимумы и минимумы производной! Мы считаем точки, в которых производная функции обращается в ноль (т.е. пересекает ось (x)).

Видео:Найти точки экстремума функцииСкачать

Как найти точки максимумов или минимумов функции по графику производной (7 задание ЕГЭ)?

Чтобы ответить на этот вопрос, нужно вспомнить еще два важных правил:

— Производная положительна там, где функция возрастает.
— Производная отрицательна там, где функция убывает.

С помощью этих правил давайте найдем на графике производной точки минимума и максимума функции.

Понятно, что минимумы и максимумы надо искать среди точек экстремумов, т.е. среди (-13), (-11), (-9),(-7) и (3).

Чтобы проще было решать задачу расставим на рисунке сначала знаки плюс и минус, обозначающие знак производной. Потом стрелки – обозначающие возрастание, убывания функции.

Начнем с (-13): до (-13) производная положительна т.е. функция растет, после — производная отрицательна т.е. функция падает. Если это представить, то становится ясно, что (-13) – точка максимума.

(-11): производная сначала положительна, а потом отрицательна, значит функция возрастает, а потом убывает. Опять попробуйте это мысленно нарисовать и вам станет очевидно, что (-11) – это минимум.

(- 9): функция возрастает, а потом убывает – максимум.

Все вышесказанное можно обобщить следующими выводами:

— Функция имеет максимум там, где производная равна нулю и меняет знак с плюса на минус.
— Функция имеет минимум там, где производная равна нулю и меняет знак с минуса на плюс.

Видео:Задание 12 ЕГЭ по математике #54Скачать

Как найти точки максимумов и минимумов если известна формула функции (12 задание ЕГЭ)?

Чтобы ответить на этот вопрос, нужно делать все то же, что и в предыдущем пункте: находить где производная положительна, где отрицательна и где равна нулю. Чтобы было понятнее напишу алгоритм с примером решения:

1. Найдите производную функции (f'(x)).
2. Найдите корни уравнения (f'(x)=0).
3. Нарисуйте ось (x) и отметьте на ней точки полученные в пункте 2, изобразите дугами промежутки, на которые разбивается ось. Подпишите над осью (f'(x)), а под осью (f(x)).
4. Определите знак производной в каждом промежутке (методом интервалов).
5. Поставьте знак производной в каждом промежутке (над осью), а стрелкой укажите возрастание (↗) или убывание (↘) функции (под осью).
6. Определите, как изменился знак производной при переходе через точки, полученные в пункте 2:
   — если (f’(x)) изменила знак с «(+)» на «(-)», то (x_1) – точка максимума;
   — если (f’(x)) изменила знак с «(-)» на «(+)», то (x_3) – точка минимума;
   — если (f’(x)) не изменила знак, то (x_2) – может быть точкой перегиба.

Всё! Точки максимумов и минимумов найдены.

Изображая на оси точки в которых производная равна нулю – масштаб можно не учитывать. Поведение функции можно показать так, как это сделано на рисунке ниже. Так будет очевиднее где максимум, а где минимум.

Пример(ЕГЭ). Найдите точку максимума функции (y=3x^5-20x^3-54).
Решение:
1. Найдем производную функции: (y’=15x^4-60x^2).
2. Приравняем её к нулю и решим уравнение:

3. – 6. Нанесем точки на числовую ось и определим, как меняется знак производной и как движется функция:

Теперь очевидно, что точкой максимума является (-2).

Видео:ЕГЭ по математике. Профильный уровень. Задание 12. Максимум и минимум функции. ЭкстремумСкачать

Экстремумы функции

Видео:Математика без Ху!ни. Экстремум функции 2х переменных.Скачать

Необходимое условие экстремума функции одной переменной

Видео:Найдите точку минимума функции y=25/x+x+25 Задание 12 ЕГЭ профильная математикаСкачать

Достаточное условие экстремума функции одной переменной

Если в точке x * выполняется условие:

Пример №1 . Найти наибольшее и наименьшее значения функции: на отрезке [1; 3].
Решение.

Критическая точка одна x₁ = 2 (f’(x)=0). Эта точка принадлежит отрезку [1;3]. (Точка x=0 не является критической, так как 0∉[1;3]).
Вычисляем значения функции на концах отрезка и в критической точке.
f(1)=9, f(2)= 5 /₂, f(3)=3 8 /₈₁
Ответ: f_min= 5 /₂ при x=2; f_max=9 при x=1

Пример №2 . С помощью производных высших порядков найти экстремум функции y=x-2sin(x) .
Решение.
Находим производную функции: y’=1-2cos(x) . Найдем критические точки: 1-cos(x)=2, cos(x)=½, x=± π /₃+2πk, k∈Z. Находим y’’=2sin(x), вычисляем , значит x= π /₃+2πk, k∈Z – точки минимума функции; , значит x=- π /₃+2πk, k∈Z – точки максимума функции.

Пример №3 . Исследовать на экстремум фцнкцию в окрестностях точки x=0.
Решение. Здесь необходимо найти экстремумы функции. Если экстремум x=0 , то выяснить его тип (минимум или максимум). Если среди найденных точек нет x = 0, то вычислить значение функции f(x=0).
Следует обратить внимание, что когда производная с каждой стороны от данной точки не меняет своего знака, не исчерпываются возможные ситуации даже для дифференцируемых функций: может случиться, что для сколь угодно малой окрестности по одну из сторон от точки x₀ или по обе стороны производная меняет знак. В этих точках приходится применять другие методы для исследования функций на экстремум.

Пример №4 . Разбить число 49 на два слагаемых, произведение которых будет наибольшим.
Решение. Обозначим x — первое слагаемое. Тогда (49-x) — второе слагаемое.
Произведение будет максимальным: x·(49-x) → max
или
49x — x 2

Видео:Свойства функции. Нули функции, экстремумы. 10 класс.Скачать

Найдите точки минимума функции на окружности

Найдите точку максимума функции

Найдем производную заданной функции:

Найдем нули производной:

Определим знаки производной функции и изобразим на рисунке поведение функции:

Искомая точка максимума

Заметим, что функция имеет разрыв при (при x = 0), и ее значение в точке минимума (при x = −17) больше, чем значение в точке максимума (при x = 17).

Найдите точку минимума функции

Область определения функции:

Найдём производную заданной функции:

Найдём нули производной:

Определим знаки производной функции и изобразим на рисунке поведение функции:

Искомая точка минимума

У меня получается при х=-1 значение функции=2.

А при х=1, значение функции= -2,

то есть точка минимума х=1.

Объясните,пожалуйста, в чём моя ошибка.

Вопрос о точке минимума, а не о минимальном значении функции

Найдите наименьшее значение функции на отрезке

Найдем производную заданной функции:

Производная обращается в нуль в точках 5 и −5. Определим знаки производной функции и изобразим на рисунке поведение функции на заданном отрезке:

Наименьшим значением функции на заданном отрезке будет ее значение в точке 5. Найдем его:

Найдите наибольшее значение функции на отрезке

Найдем производную заданной функции:

Производная обращается в нуль в точках 5 и −5, заданному отрезку принадлежит только число −5.

Наибольшим значением функции на заданном отрезке будет наибольшее из чисел и Найдем их:

Найдите точку максимума функции

Область определения функции:

Найдем производную заданной функции:

Найдем нули производной:

Определим знаки производной функции и изобразим на рисунке поведение функции:

Искомая точка максимума

Внимательный читатель может заметить, что значение функции в точке x = −4 меньше, чем в точке x = 4. Тем не менее точка −4 является точкой максимума, поскольку слева от нее функция возрастает, а справа убывает, а точка 4 является точкой минимума. Значение в точке максимума отказалось меньше, чем в точке минимума, поскольку функция имеет разрыв при x = 0.

🔥 Видео

ЕГЭ 2022: Задание 6. Количество точек экстремума функции по производнойСкачать

Точки ЭКСТРЕМУМА на графике производной / разбор ЕГЭ #27496Скачать

ЕГЭ по математике. Профильный уровень. Задание 12. Найдите точку максимума функции.Скачать

Математический анализ, 12 урок, Монотонность и экстремумы функцииСкачать

ТОЧКА МАКСИМУМА И МАКСИМУМ ФУНКЦИИ ЧАСТЬ I #математика #егэ #огэ #shorts #геометрияСкачать

Найдите точку минимума функции y=(x+17)^2*e^(30-x)Скачать

Задание 11 ЕГЭ профиль № 77491 Найдите точку минимума функции y=2x^2-5x+ln⁡x-3Скачать

Тип 11 № 26726 Найдите точку максимума функции y=〖(x-2)〗^2 e^(x-6)Скачать

Задание 12 ЕГЭ по математике #13Скачать

График функции - нахождение точек минимумаСкачать

Задание 12 ЕГЭ по математике #50Скачать

Максимум и минимум функции - bezbotvyСкачать

Нахождение точек экстремума функции по графикам. ЕГЭ. Задание В8Скачать