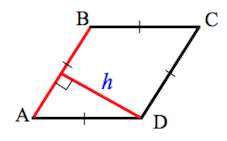
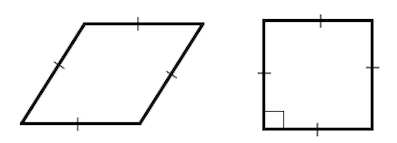В данной публикации мы рассмотрим определение, свойства и признаки (с рисунками) одной из основных геометрических фигур – ромба.
Видео:Все про РОМБ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // Геометрия 8 классСкачать

Определение ромба
Ромб – это фигура на плоскости; разновидность параллелограмма, у которого все четыре стороны равны и попарно параллельны. Обычно ромб обозначается названиями его вершин (например, ABCD), а длина его стороны – строчной латинской буквой (например, a).
Примечание: квадрат является частным случаем ромба.
Видео:В четырехугольник вписан ромб, стороны которого параллельны диагоналям четырехугольника.Скачать

Свойства ромба
Свойство 1
Противоположные углы ромба равны между собой, а сумма соседних углов составляет 180°.
Свойство 2
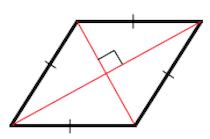
Диагонали ромба пересекаются под прямым углом и в точке пересечения делятся пополам.
В результате пересечения диагоналей ромб делится на 4 прямоугольных треугольника: ΔAEB, ΔBEC, ΔAED и ΔDEC.
Свойство 3
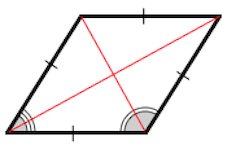
Диагонали ромба являются биссектрисами его углов.
Свойство 4
Сторону ромба a можно найти через его диагонали d1 и d2 (согласно теореме Пифагора).
- a – гипотенуза любого из 4 прямоугольных треугольников (например, ΔBEC );
- половины диагоналей d1 и d2 – катеты треугольников.
Свойство 5
В любой ромб можно вписать окружность, центр которой лежит на пересечении его диагоналей.
Радиус вписанной в ромб окружности r вычисляется по формуле:
Видео:Параллелограмм, прямоугольник, ромб,квадрат,трапеция, все свойства и определения!!!Скачать

Признаки ромба
Параллелограмм является ромбом только в том случае, если для него верно одно из следующих утверждений:
- Его диагонали пересекаются под прямым углом.
- Если его диагонали являются биссектрисами его углов.
- Две смежные стороны равны (следовательно, все стороны равны).
Примечание: Любой четырехугольник, стороны которого равны, является ромбом.
Видео:Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Ромб это четырехугольник в котором все стороны
Определение 1. Ромб − это параллелограмм, у которого все стороны равны.
На рисунке 1 изображен ромб ABCD.
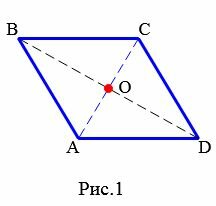 |
Определение 2. Ромб − это четырехугольник, у которого все стороны равны.
Ромб разделяет плоскость на две части, одна из которых называется внутренней областью ромба, а другая внешней областью ромба.
Объединение ромба и ограниченной им части плоскости также называют ромбом.
Видео:Ромб. 8 класс.Скачать

Свойства ромба
Поскольку ромб является параллелограммом, то имеет следующие свойства:
- 1. У ромба противолежащие углы равны (( small angle A = angle C, ; angle B = angle D.) )
- 2. У ромба противолежащие стороны равны (( small AB = DC, ; BC=AD.) )
- 3. У ромба противолежащие стороны параллельны ( small( AB || DC, ; BC || AD).)
- 4. У ромба соседние углы дополняют друг друга до 180° ( small ( angle A +angle B=180°, ) ( small angle C + angle D=180°).)
- 5. Диагонали ромба точкой пересечения делятся пополам ( small ( AO = OC, ) ( small BO=OD).)
Ромб имеет также и следующие свойства:
- 6. Диагонали ромба пересекаются под прямым углом (( small AC perp BD.) )
- 7. Диагонали ромба являются биссектрисами его углов (( small angle ABD = angle CBD, ) ( small angle ADB = angle CDB, ) ( small angle DAC = angle BAC, ) ( small angle BCA = angle DCA. ))
- 8. В любой ромб можно вписать окружность, центр которой лежит на пересечении его диагоналей.
- 9. Сумма квадратов диагоналей ромба равна квадрату стороны, умноженная на четыре ( small (AC^2+BD^2=4AB^2). )
Докажем свойства 6 и 7, сформулировав следующую теорему:
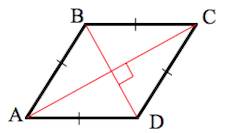
Теорема 1. Диагонали ромба перпендикулярны и являются биссектрисами его углов.
Доказательство. По определению 1, ( small AD = DC ) (Рис.2). Следовательно треугольник ( small DAC ) равнобедренный. Тогда ( small angle DCO = angle DAO. ) Учитывая, что ( small AO = OC ) (свойство 5 ромба), получим, что треугольники ( small DOA ) и ( small DOC ) равны по двум сторонам и углу между ними (см. статью Треугольники. Признаки равенства треугольников). Тогда равны углы DOC и DOA. Но эти углы смежные и их сумма равна 180°. Следовательно ( small angle DOC= angle DOA=90°. ) То есть диагонали AC и BD перпендикулярны.
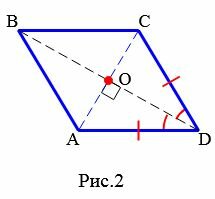 |
Из равенства треугольников ( small DOA ) и ( small DOC ) также следует, что ( small angle CDO= angle ADO,) следовательно BD является биссектрисой угла ADС, то есть BD является биссектрисой ромба ABCD.
Видео:Геометрия 8. Урок 4 - Прямоугольник, ромб, квадрат - свойства и признаки.Скачать

Признаки ромба
Признак 1. Если смежные стороны параллелограмма равны, то этот параллелограмм − ромб.
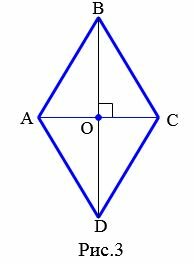 |
Доказательство. Пусть смежные стороны параллелограмма ABCD равны. То есть имеем: AB=BC (Рис.3). У параллелограмма противоположные стороны равны (Свойство 1 статьи Параллелограмм). Тогда DC=AB=BC=AD. То есть все стороны параллелограмма равны и по определению 1, этот параллелограмм является ромбом.
Признак 2. Если диагонали параллелограмма перпендикулярны, то этот параллелограмм − ромб.
Доказательство. Пусть диагонали параллелограмма ABCD перпендикулярны (Рис.3). Рассмотрим прямоугольные треугольники AOB и COB. Так как у параллелограмма диагонали точкой пересечения разделяются пополам (Свойство 2 статьи Параллелограмм), то AO=OC. Тогда прямоугольные треугольники AOB и COB равны по двум катетам (AO=OC, BO общий катет (см. статью Прямоугольный треугольник. Свойства, признаки равенства)). Следовательно AB=BC. Тогда по признаку 1 этот параллелограмм является ромбом.
Признак 3. Если диагональ параллелограмма является биссектрисой его угла, то этот параллелограмм − ромб.
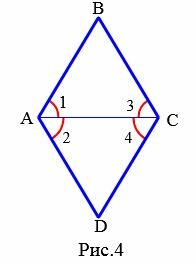 |
Доказательство. Пусть диагональ AC параллелограмма ABCD является биссектрисой угла BAD (Рис.4). Тогда ( small angle 1= angle 2 .) У параллелограмма ABCD ( small AB || DC .) Тогда для параллельных прямых AB и DC и секущей AC справедливо равенство ( small angle 1= angle 4 .) (см теорему 1 статьи Теоремы об углах, образованных двумя параллельными прямыми и секущей). Аналогично, для параллельных прямых BC и AD и секущей AC справедливо равенство ( small angle 2= angle 3 .) Так как ( small angle 1= angle 2 ,) то ( small angle 1= angle 2=angle 3= angle 4 .) Из ( small angle 1= angle 3) следует, что треугольник ABC равнобедренный (Признак 2 статьи Равнобедренный треугольник). Тогда AB=BC. У параллелограмма противоположные стороны равны (Свойство 1 статьи Параллелограмм). Тогда AB=BC=CD=DA. То есть все стороны параллелограмма равны и по определению 1, этот параллелограмм является ромбом.
Признак 4. Если стороны четырехугольника равны, то этот четырехугольник − ромб.
Доказательство. Пусть у четырехугольника все стороны равны. Тогда этот четырехугольник является параллелограммом (признак 2 статьи Параллелограмм). А по определению 1, этот параллелограмм является ромбом.
Видео:Площадь ромба. Легче понять...Скачать
Ромб. Свойства и признаки ромба
Ромб – это параллелограмм, у которого все стороны равны.
Если у ромба – прямые углы, то он называется квадратом.
Видео:8 класс, 8 урок, Ромб и квадратСкачать

Свойства ромба
1. Поскольку ромб – это параллелограмм, то все свойства параллелограмма верны для ромба.
Помимо этого:
2. Диагонали ромба перпендикулярны.
3. Диагонали ромба являются биссектрисами его углов.
4. Сумма квадратов диагоналей равна квадрату стороны, умноженному на 4.
Видео:Я СДЕЛАЛ СВОЙ ДОМ ТРЕУГОЛЬНЫМ В МАЙНКРАФТ | Компот MinecraftСкачать
Признаки ромба
Чтобы параллелограмм оказался ромбом, необходимо выполнение одного из следующих условий:
1. Все стороны параллелограмма равны между собой ().
2. Диагонали пересекаются под прямым углом ().
3. Диагонали параллелограмма являются биссектрисами его углов.
Видео:Геометрия 7 класса в одной задаче. Геометрия 7 класс кратко | МатематикаСкачать

Площадь ромба
Смотрите также таблицу-шпаргалку «Площади простейших фигур» здесь.
Чтобы не потерять страничку, вы можете сохранить ее у себя:
🔥 Видео
Ромб, признаки. 8 класс.Скачать

Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

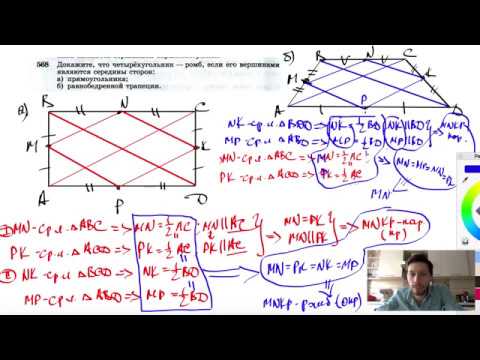
№568. Докажите, что четырехугольник — ромб, если его вершинами являются середины сторон:Скачать
Геометрия 8 класс: Ромб и квадратСкачать

8 класс, 3 урок, ЧетырехугольникСкачать

Геометрия 8 класс (Урок№6 - Прямоугольник. Ромб. Квадрат.)Скачать

№175. Докажите, что если все ребра тетраэдра равны, то все его двугранные углы также равны.Скачать

Геометрия Признак ромба Если диагонали параллелограмма перпендикулярны, то этот параллелограмм ромбСкачать

Геометрия 10 класс (Урок№2 - Четырехугольники.)Скачать

8 класс, 4 урок, ПараллелограммСкачать