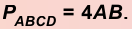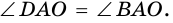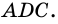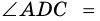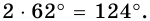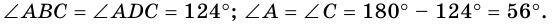Ромб это четырехугольник в котором диагонали взаимно перпендикулярны а противолежащие стороны

Ромбом называют параллелограмм, у которого все стороны равны (рис. 48).

Так как ромб является параллелограммом, то он имеет все свойства параллелограмма.

1. Сумма любых двух соседних углов ромба равна 180°.

2. У ромба противолежащие углы равны.

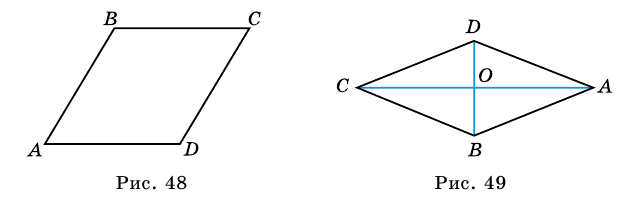
3. Диагонали ромба точкой пересечения делятся пополам.

4. Периметр ромба

Кроме того, ромб имеет еще и такое свойство.

5. Диагонали ромба взаимно перпендикулярны и делят его углы пополам.

Доказательство:

Пусть и — диагонали ромба (рис. 49), — точка их пересечения. Поскольку и то — медиана равнобедренного треугольника проведенная к основанию Поэтому является также высотой и биссектрисой треугольника

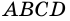
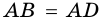
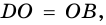
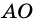
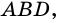
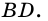
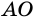
Следовательно, 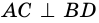и

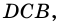
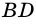
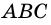
Аналогично можно доказать, что диагональ АС делит пополам угол а диагональ делит пополам углы и

Пример:

Угол между высотой и диагональю ромба проведенными из одной вершины, равен 28°. Найдите углы ромба.

Решение:

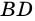
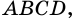
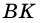
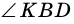
Пусть — диагональ ромба а — его высота (рис. 50), = 28°.

1) В

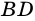
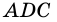
2) Так как делит угол пополам, то

3) Тогда

Ответ. 124°, 56°, 124°, 56°.

Рассмотрим признаки ромба.

Теорема (признаки ромба). Если в параллелограмме: 1) две соседние стороны равны, или 2) диагонали пересекаются под прямым углом, или 3) диагональ делит пополам углы параллелограмма, — то параллелограмм является ромбом.

Доказательство:

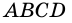
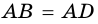
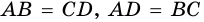
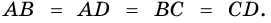
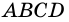
1) Пусть — параллелограмм (рис. 48). Так как (по условию) и (по свойству параллелограмма), то Следовательно, — ромб.

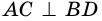
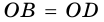
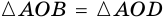
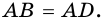
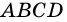
2) Пусть (рис. 49). Поскольку (по свойству параллелограмма), то (по двум катетам). Следовательно, По п. 1 этой теоремы — ромб.

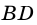
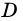
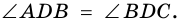
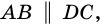
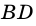
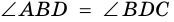
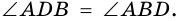
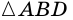
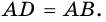
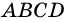
3) Диагональ делит пополам угол параллелограмма (рис. 49), то есть Так как — секущая, то (как внутренние накрест лежащие). Следовательно, Поэтому по признаку равнобедренного треугольника — равнобедренный и По п. 1 этой теоремы — ромб.

Пример:

Докажите, что если в четырехугольнике все стороны равны, то этот четырехугольник — ромб.

Доказательство:

Пусть 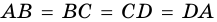(рис. 48).

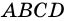
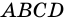
1) Так как противолежащие стороны четырехугольника попарно равны, то — параллелограмм по признаку параллелограмма.

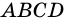
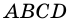
2) У параллелограмма соседние стороны равны. Поэтому — ромб (по признаку ромба).

Слово «ромб» греческого происхождения, которое в древние времена означало вращающееся тело, веретено, волчок. Ромб тогда связывали с сечением веретена, на которое намотаны нити.

В «Началах» Евклида термин «ромб» встречается единожды, а свойства ромба Евклид вообще не рассматривал.

• Квадрат и его свойства
• Трапеция и ее свойства
• Площадь трапеции
• Центральные и вписанные углы
• Четырехугольники и окружность
• Параллелограмм, его свойства и признаки
• Площадь параллелограмма
• Прямоугольник и его свойства

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Видео:Геометрия Признак ромба Если диагонали параллелограмма перпендикулярны, то этот параллелограмм ромбСкачать

Тема урока: «Прямоугольник. Ромб. Квадрат»

Разделы: Математика

Цели урока:

• закрепить теоретический материал по теме “Прямоугольник. Ромб. Квадрат”;
• совершенствовать навыки решения задач по теме;
• сформировать положительную мотивацию к урокам математики.

Видео:Все про РОМБ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // Геометрия 8 классСкачать

Ход урока

I. Организационный момент.

Сообщить тему урока, сформулировать цели урока.

II. Актуализация знаний учащихся.

1. Теоретическая самостоятельная работа

Заполнить таблицу, отметив знаки + (да), — (нет).

2. Проверочный тест

1. Любой прямоугольник является:

а) ромбом; б) квадратом; в) параллелограммом; г) нет правильного ответа.

2. Если в четырехугольнике диагонали перпендикулярны, то этот четырехугольник — …

а) ромб; б) квадрат; в) прямоугольник; г) нет правильного ответа.

3. Ромб – это четырехугольник, в котором …

а) диагонали точкой пересечения делятся пополам и равны;

б) диагонали взаимно перпендикулярны и точкой пересечения делятся пополам;

в) противолежащие углы равны, а противолежащие стороны параллельны;

г) нет правильного ответа.

1. Любой ромб является:

а) квадратом; б) прямоугольником; в) параллелограммом; г) нет правильного ответа.

2. Если в параллелограмме диагонали перпендикулярны, то этот параллелограмм — …

а) ромб; б) квадрат; в) прямоугольник; г) нет правильного ответа.

3. Прямоугольник – это четырехугольник, в котором …

а) противолежащие стороны параллельны, а диагонали равны;

б) диагонали точкой пересечения делятся пополам и являются биссектрисами его углов;

в) два угла прямые и две стороны равны;

г) нет правильного ответа.

1 вариант: 1 – в); 2 – г); 3 – б).

2 вариант: 1 – в); 2 – а); 3 – а).

III. Проверка усвоения теоретического материала.

Два ученика работают у доски. .Первый доказывает один из признаков параллелограмма, второй- диагоналей прямоугольника. В это время остальные учащиеся устно решают задачи по готовым чертежам.

После решения задач заслушиваются ответы учащихся у доски.

Решение задач у доски с краткой записью.

1) Найдите углы ромба, если его диагонали составляют с его стороной углы, один из которых на 30° меньше другого.

Диагонали ромба взаимно перпендикулярны, поэтому треугольник АОВ – прямоугольный (рис.1). Пусть в D АОВ АВО = х, тогда ВАО = х + 30° , значит АВО + ВАО = х + х + 30 ° = 90° , и х = 30° .

АВО = 30° , ВАО = 60° , а т.к. диагонали ромба являются биссектрисами его углов, то ВАD = 120° , АВС = 60° .

Противолежащие углы в ромбе равны, тогда АDС = АВС = 60° , ВСD = BAD = 120° .

Ответ: 60 ° ,120° , 60° , 120° .

2) Угол между диагоналями прямоугольника равен 80° . Найдите углы между диагональю прямоугольника и его сторонами.

Диагонали прямоугольника равны и точкой пересечения делятся пополам, значит ВО = ВD/2 = АС/2 =АО и D АОВ – равнобедренный (рис.2.), тогда ОАВ = ОВА = 50° . В прямоугольнике все углы прямые, тогда ОАD = ВАD — ОАВ = 90 ° – 50° = 40° .

3) В ромбе ABCD биссектриса угла ВAC пересекает сторону ВС и диагональ BD соответственно в точках М и N. Найдите АNВ, если АМС = 120° .

В ромбе (рис.3.) противолежащие углы равны и диагонали являются биссектрисами его углов, т.е. ВАС = ВАD : 2 =ВСD : 2 = ВСА. Т.к. АМ – биссектриса ВАС, а ВАС = ВСА, то МАС = МСА : 2.

В треугольнике АМС МАС + МСА = 180 ° — АМС = 180 ° -120° = 60° . МАС = МСА : 2, тогда МАС = 20° , ВАС = 40° .

В ромбе диагонали взаимно перпендикулярны, треугольник АОВ – прямоугольный, АВО = 90° — ВАО = 50° . Рис.3.

В треугольнике АВN BAN = МАС = 20° , ABN = 50° , тогда

ANB = 180° – (20° + 50° ) = 110° .

Ответ: ANB = 110° .

IV. Самостоятельная работа обучающего характера с последующей самопроверкой.

1) В ромбе АВСD диагонали пересекаются в точке О, А = 80 ° . Найдите углы треугольника ВОС.

а) Рис.4. А = С = 80° ; СО – биссектриса С, тогдаОСВ = 40° ; . D = B = (360° -( А + С ))/2=100° ;

б) D СОВ – прямоугольный, ВОС = 90° , ОСВ =40° , ОВС = 100° /2=50°

Видео:Ромб. 8 класс.Скачать

Ромб это четырехугольник в котором диагонали взаимно перпендикулярны а противолежащие стороны

С помощю этого онлайн калькулятора ромба можно найти неизвестные этлементы ромба по известным элементам. Для нахождения неизвестных элементов ромба, введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть смотрите ниже.

Видео:№410. Является ли четырехугольник квадратом, если его диагонали: а) равны и взаимноСкачать

Определение ромба

Определение 1. Ромб − это параллелограмм, у которого все стороны равны.

На рисунке 1 изображен ромб ABCD.

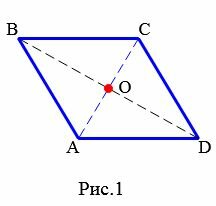Определение 2. Ромб − это четырехугольник, у которого все стороны равны.

Ромб разделяет плоскость на две части, одна из которых называется внутренней областью ромба, а другая внешней областью ромба.

Объединение ромба и ограниченной им части плоскости также называют ромбом.

Видео:Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Свойства ромба

Поскольку ромб является параллелограммом, то имеет следующие свойства:

• 1. У ромба противолежащие углы равны (( small angle A = angle C, ; angle B = angle D.) )
• 2. У ромба противолежащие стороны равны (( small AB = DC, ; BC=AD.) )
• 3. У ромба противолежащие стороны параллельны ( small( AB || DC, ; BC || AD).)
• 4. У ромба соседние углы дополняют друг друга до 180° ( small ( angle A +angle B=180°, ) ( small angle C + angle D=180°).)
• 5. Диагонали ромба точкой пересечения делятся пополам ( small ( AO = OC, ) ( small BO=OD).)

Ромб имеет также и следующие свойства:

• 6. Диагонали ромба пересекаются под прямым углом (( small AC perp BD.) )
• 7. Диагонали ромба являются биссектрисами его углов (( small angle ABD = angle CBD, ) ( small angle ADB = angle CDB, ) ( small angle DAC = angle BAC, ) ( small angle BCA = angle DCA. ))
• 8. В любой ромб можно вписать окружность, центр которой лежит на пересечении его диагоналей.
• 9. Сумма квадратов диагоналей ромба равна квадрату стороны, умноженная на четыре ( small (AC^2+BD^2=4AB^2). )

Докажем свойства 6 и 7, сформулировав следующую теорему:

Теорема 1. Диагонали ромба перпендикулярны и являются биссектрисами его углов.

Доказательство. По определению 1, ( small AD = DC ) (Рис.2). Следовательно треугольник ( small DAC ) равнобедренный. Тогда ( small angle DCO = angle DAO. ) Учитывая, что ( small AO = OC ) (свойство 5 ромба), получим, что треугольники ( small DOA ) и ( small DOC ) равны по двум сторонам и углу между ними (см. статью Треугольники. Признаки равенства треугольников). Тогда равны углы DOC и DOA. Но эти углы смежные и их сумма равна 180°. Следовательно ( small angle DOC= angle DOA=90°. ) То есть диагонали AC и BD перпендикулярны.

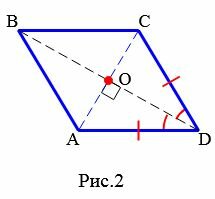Из равенства треугольников ( small DOA ) и ( small DOC ) также следует, что ( small angle CDO= angle ADO,) следовательно BD является биссектрисой угла ADС, то есть BD является биссектрисой ромба ABCD.

Видео:Если в четырёхугольнике диагонали перпендикулярны ... | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Признаки ромба

Признак 1. Если смежные стороны параллелограмма равны, то этот параллелограмм − ромб.

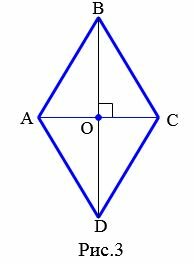Доказательство. Пусть смежные стороны параллелограмма ABCD равны. То есть имеем: AB=BC (Рис.3). У параллелограмма противоположные стороны равны (Свойство 1 статьи Параллелограмм). Тогда DC=AB=BC=AD. То есть все стороны параллелограмма равны и по определению 1, этот параллелограмм является ромбом.

Признак 2. Если диагонали параллелограмма перпендикулярны, то этот параллелограмм − ромб.

Доказательство. Пусть диагонали параллелограмма ABCD перпендикулярны (Рис.3). Рассмотрим прямоугольные треугольники AOB и COB. Так как у параллелограмма диагонали точкой пересечения разделяются пополам (Свойство 2 статьи Параллелограмм), то AO=OC. Тогда прямоугольные треугольники AOB и COB равны по двум катетам (AO=OC, BO общий катет (см. статью Прямоугольный треугольник. Свойства, признаки равенства)). Следовательно AB=BC. Тогда по признаку 1 этот параллелограмм является ромбом.

Признак 3. Если диагональ параллелограмма является биссектрисой его угла, то этот параллелограмм − ромб.

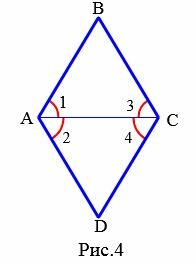Доказательство. Пусть диагональ AC параллелограмма ABCD является биссектрисой угла BAD (Рис.4). Тогда ( small angle 1= angle 2 .) У параллелограмма ABCD ( small AB || DC .) Тогда для параллельных прямых AB и DC и секущей AC справедливо равенство ( small angle 1= angle 4 .) (см теорему 1 статьи Теоремы об углах, образованных двумя параллельными прямыми и секущей). Аналогично, для параллельных прямых BC и AD и секущей AC справедливо равенство ( small angle 2= angle 3 .) Так как ( small angle 1= angle 2 ,) то ( small angle 1= angle 2=angle 3= angle 4 .) Из ( small angle 1= angle 3) следует, что треугольник ABC равнобедренный (Признак 2 статьи Равнобедренный треугольник). Тогда AB=BC. У параллелограмма противоположные стороны равны (Свойство 1 статьи Параллелограмм). Тогда AB=BC=CD=DA. То есть все стороны параллелограмма равны и по определению 1, этот параллелограмм является ромбом.

Признак 4. Если стороны четырехугольника равны, то этот четырехугольник − ромб.

Доказательство. Пусть у четырехугольника все стороны равны. Тогда этот четырехугольник является параллелограммом (признак 2 статьи Параллелограмм). А по определению 1, этот параллелограмм является ромбом.

📽️ Видео

№408. Докажите, что параллелограмм является ромбом, если: а) его диагонали взаимноСкачать

Геометрия 8. Урок 4 - Прямоугольник, ромб, квадрат - свойства и признаки.Скачать

Геометрия Доказательство Диагонали ромба перпендикулярны и являются биссектрисами его угловСкачать

Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

Ромб, признаки. 8 класс.Скачать

Один отрезок - диагональ четырёхугольника, диаметр окружности, высота ромбаСкачать

Параллелограмм, прямоугольник, ромб,квадрат,трапеция, все свойства и определения!!!Скачать

8 класс, 3 урок, ЧетырехугольникСкачать

№478. В выпуклом четырехугольнике диагонали взаимно перпендикулярны. Докажите, что площадьСкачать

8 класс, 8 урок, Ромб и квадратСкачать

8 класс, 4 урок, ПараллелограммСкачать

Геометрия 8 класс (Урок№6 - Прямоугольник. Ромб. Квадрат.)Скачать

РОМБ . §5 геометрия 8 классСкачать

Геометрия 10 класс (Урок№2 - Четырехугольники.)Скачать