Решение задач по теме скалярные и векторные величины действия над векторами (6 видео)

Примеры решения задач с векторами

Вектора применяются во многих науках, таких как: математика, физика, геометрия и многих других прикладных науках. На практике, они позволяют не делать лишних операций и сократить время выполнения задач. Поэтому, будущим специалистам очень важно понять теорию векторов и научиться решать задачи с ними.

Перед изучением примеров решения задач советуем изучить теоретический материал по векторам, прочитать все определения и свойства. Список тем находится в правом меню.

Содержание

Координаты вектора
Скалярные и векторные величины. Действия над векторами
Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся
Векторы на ЕГЭ по математике. Действия над векторами
Сложение векторов
Вычитание векторов
Умножение вектора на число
Скалярное произведение векторов
Онлайн-курс «Математика 10+11 100 баллов»
🎦 Видео

Координаты вектора

Теоретический материал по теме — координаты вектора.

Видео:Урок 8. Векторные величины. Действия над векторами.Скачать

Скалярные и векторные величины. Действия над векторами

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся

Сертификат и скидка на обучение каждому участнику

План-конспект урока по теме «Скалярные и векторные величины. Действия над векторами»

Тема: «Скалярные и векторные величины. Действия над векторами»

Образовательная : Обеспечить и сформировать осознанное усвоение знаний о скалярных и векторных величинах, а также изучить действия над векторами;

Развивающая : Продолжить развитие навыков самостоятельной деятельности, навыков работы в группах.

Воспитательная : Формировать познавательный интерес к новым знаниям; воспитывать дисциплину поведения.

Тип урока: урок усвоения новых знаний

Оборудование и источники информации:

Исаченкова, Л. А. Физика : учеб. для 9 кл. учреждений общ. сред. образования с рус. яз. обучения / Л. А. Исаченкова, Г. В. Пальчик, А. А. Сокольский ; под ред. А. А. Сокольского. Минск : Народная асвета, 2015

Организационный момент(3 мин)

Актуализация опорных знаний(5 мин)

Изучение нового материала (18 мин)

Закрепление знаний (15 мин)

Итоги урока(5 мин)

Здравствуйте, садитесь! (Проверка присутствующих). Сегодня на уроке мы должны разобраться со скалярными и векторными величинами, а также научиться действиям с векторами. А это значит, что Тема урока : Скалярные и векторные величины. Действия над векторами.

Актуализация опорных знаний

В курсе физики мы рассматривали различные величины. Для определения одних (массы, пути, температуры) достаточно знать числовое значение и единицу измерения. Например, m = 25 кг, s = 10 км. Такие физические величины называются скалярными. Для других величин необходимо знать еще и направление. Их называют векторными. Векторной, например, является известная вам физическая величина — сила. Почему?

Изучение нового материала

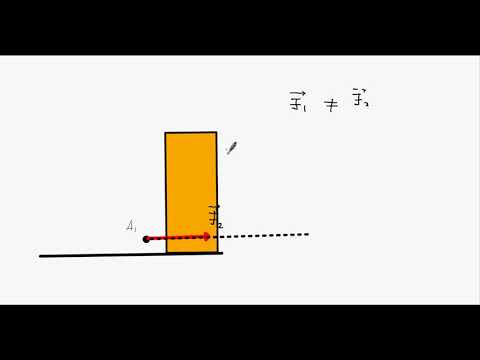
На рисунке 21, а, б девочка действует на санки силой, имеющей одно и то же числовое значение. Но в первом случае санки лишь сильнее погрузились в снег, а во втором — пришли в движение. Значит, сила определяется не только числовым значением, но и направлением. Сила — величина векторная.

Векторной величиной является и скорость движения (подумайте почему), и многие другие физические величины.

Что нужно знать о векторных величинах?

1. Векторные величины (векторы) характеризуются числовым значением и направлением в пространстве.

Вектор изображают в виде направленного отрезка (стрелки). Стрелка указывает, куда направлен вектор. Длина стрелки определяет числовое значение вектора (рис. 22).

Вектор обозначают буквой, над которой поставлена стрелка, например . Его можно обозначить также двумя буквами со стрелкой над ними, например , где точка А — начало вектора , точка В — конец вектора (см. рис. 22).

Числовое значение вектора называется модулем.

Модуль вектора обозначают буквой без стрелки или символом |…| На пример, на рисунке 22 модуль вектора равен

а = | | = | | = 4.

Модуль любого (не равного нулю) вектора — число положительное.

2.Векторы равны между собой, если равны их модули и одинаковы их направления.

Равные векторы лежат на одной и той же прямой или на параллельных прямых и направлены в одну и ту же сторону. На рисунке 23 , Однако , хотя модули векторов и одинаковы. Одного только равенства модулей для равенства векторов недостаточно!

3.Угол между векторами.

Чтобы найти угол между векторами (рис. 24, а), нужно совместить начала этих векторов (рис. 24, б). Если направ ления векторов одинаковы, то = 0° (рис. 24, в), если противоположны, то = 180° (рис. 24, г).

4.Умножение вектора на число.

Произведение вектора на число есть вектор . Чему равен модуль вектора ? Куда он направлен?

Модуль вектора равен = || • а.

Направление вектора совпадает с направлением вектора , если > 0, и противоположно вектору а, если

Рассмотрите внимательно рисунок 25. Вы увидите, что, умножив вектор а на 2, мы увеличили его в два раза, а умножив на 0,5, — в два раза уменьшили (см. рис. 25, а, б). При умножении на (-3) модуль вектора увеличивается в три раза и вектор поворачивается на 180° (см. рис. 25, а, в).

Вектор d называется противоположным вектору а, если d = -а. У векторов d и а одинаковые модули, но противоположные направления (см. рис. 25, а, г).

Если векторы а и b направлены одинаково, то их сумма — это вектор с того

же направления, имеющий модуль с = а + b (рис. 26, а ).

Если же направления векторов а и b противоположны (рис. 26, б), то их сумма — вектор с направлен так, как вектор, модуль которого больше. При этом модуль вектора с равен разности модулей слагаемых векторов.

А как сложить векторы, направленные под любым углом друг к другу?

а) Правило параллелограмма.

Совместим начала векторов а и b (рис. 27, а). Построим параллелограмм ABCD , принимая векторы a и b за его стороны. Суммой векторов а и b является вектор с, совпадающий с диагональю АС параллелограмма:

б) Правило треугольника.

Совместим конец вектора а и начало вектора b (рис. 27, б). Вектор с,

проведенный из начала вектора а в конец вектора b , равен сумме а + b .

Сравнив рисунки 27, а и 27, б, докажите, что правило треугольника следует из правила параллелограмма.

Совместим начала векторов а и b (рис. 28). Проведем вектор d из конца вычитаемого вектора b в конец уменьшаемого вектора а (см. рис. 28). Вектор d есть искомая разность:

Найдите самостоятельно вектор f = b -а. В чем различие векторов d и f ? Проверьте на примерах, что а — b =а +(- b ). Значит, разность а — b можно найти, прибавляя к вектору а вектор, противоположный вектору b .

Чтобы найти сумму нескольких векторов (например, , , , а ₄ ), каждый следующий вектор нужно проводить из конца предыдущего (рис. 29).

Замыкающий вектор с, проведенный из начала первого вектора a , в конец последнего а ₄ есть сумма данных векторов: с = + а ₂ + +. Такой способ сложения называется правилом многоугольника. Оно следует из правила треугольника.

9. Модуль суммы векторов.

Не путайте модуль суммы векторов, т.е. | a + b | и сумму их модулей | a | +| b |. Равенство | a + b | = | a | + | b | выполняется только для одинаково направленных векторов. В остальных случаях | a + b | a | + | b |: модуль суммы меньше суммы модулей. Так получается потому, что в любом треугольнике (см. рис. 27, б) длина одной стороны меньше суммы длин двух других сторон. Проверьте это на примерах.

Пусть вектор а равен вектору b . Тогда их разность a — b =0. Нуль-вектор 0 не имеет направления, а его модуль равен нулю: | |0|= 0.

Векторные величины характеризуются числовым значением и направлением, скалярные — только числовым значением.

Сумму двух векторов находят по правилу параллелограмма или треугольника.

Разность двух векторов находят, проводя вектор из конца вычитаемого вектора в конец уменьшаемого (при совмещенных началах векторов).

Разность векторов а — b можно найти как сумму а + (- b ).

Произведение вектора а на число есть вектор b = a . Его направление совпадает с направлением вектора а, если > О, и противоположно вектору а, если b равен b = || • а.

Итак, подведем итоги. Что вы сегодня узнали на уроке?

Организация домашнего задания

Сегодня на уроке я узнал…

Знания, которые я получил на уроке, пригодятся

Видео:Основы кинематики. Тема 2. Скалярные и векторные величины. Действия над векторамиСкачать

Векторы на ЕГЭ по математике. Действия над векторами

Стандартное определение: «Вектор — это направленный отрезок». Обычно этим и ограничиваются знания выпускника о векторах. Кому нужны какие-то «направленные отрезки»?

А в самом деле, что такое векторы и зачем они?
Прогноз погоды. «Ветер северо-западный, скорость 18 метров в секунду». Согласитесь, имеет значение и направление ветра (откуда он дует), и модуль (то есть абсолютная величина) его скорости.

Величины, не имеющие направления, называются скалярными. Масса, работа, электрический заряд никуда не направлены. Они характеризуются лишь числовым значением — «сколько килограмм» или «сколько джоулей».

Физические величины, имеющие не только абсолютное значение, но и направление, называются векторными.

Скорость, сила, ускорение — векторы. Для них важно «сколько» и важно «куда». Например, ускорение свободного падения направлено к поверхности Земли, а величина его равна 9,8 м/с 2 . Импульс, напряженность электрического поля, индукция магнитного поля — тоже векторные величины.

Вы помните, что физические величины обозначают буквами, латинскими или греческими. Стрелочка над буквой показывает, что величина является векторной:

Вот другой пример.
Автомобиль движется из A в B . Конечный результат — его перемещение из точки A в точку B , то есть перемещение на вектор .

Теперь понятно, почему вектор — это направленный отрезок. Обратите внимание, конец вектора — там, где стрелочка. Длиной вектора называется длина этого отрезка. Обозначается: или

До сих пор мы работали со скалярными величинами, по правилам арифметики и элементарной алгебры. Векторы — новое понятие. Это другой класс математических объектов. Для них свои правила.

Когда-то мы и о числах ничего не знали. Знакомство с ними началось в младших классах. Оказалось, что числа можно сравнивать друг с другом, складывать, вычитать, умножать и делить. Мы узнали, что есть число единица и число ноль.
Теперь мы знакомимся с векторами.

Понятия «больше» и «меньше» для векторов не существует — ведь направления их могут быть разными. Сравнивать можно только длины векторов.

А вот понятие равенства для векторов есть.
Равными называются векторы, имеющие одинаковые длины и одинаковое направление. Это значит, что вектор можно перенести параллельно себе в любую точку плоскости.
Единичным называется вектор, длина которого равна 1 . Нулевым — вектор, длина которого равна нулю, то есть его начало совпадает с концом.

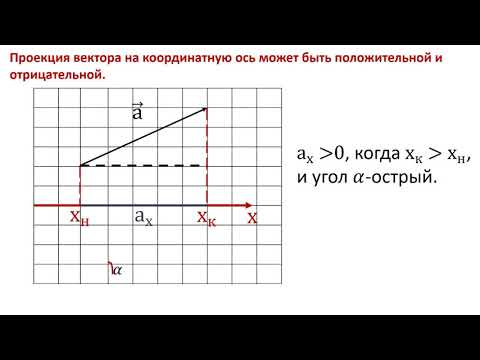
Удобнее всего работать с векторами в прямоугольной системе координат — той самой, в которой рисуем графики функций. Каждой точке в системе координат соответствуют два числа — ее координаты по x и y , абсцисса и ордината.
Вектор также задается двумя координатами:

Здесь в скобках записаны координаты вектора — по x и по y .
Находятся они просто: координата конца вектора минус координата его начала.

Если координаты вектора заданы, его длина находится по формуле

Видео:СКАЛЯРНОЕ УМНОЖЕНИЕ ВЕКТОРОВ ЧАСТЬ I #математика #егэ #огэ #формулы #профильныйегэ #векторыСкачать

Сложение векторов

Для сложения векторов есть два способа.

1 . Правило параллелограмма. Чтобы сложить векторы и , помещаем начала обоих в одну точку. Достраиваем до параллелограмма и из той же точки проводим диагональ параллелограмма. Это и будет сумма векторов и .

Помните басню про лебедя, рака и щуку? Они очень старались, но так и не сдвинули воз с места. Ведь векторная сумма сил, приложенных ими к возу, была равна нулю.

2 . Второй способ сложения векторов — правило треугольника. Возьмем те же векторы и . К концу первого вектора пристроим начало второго. Теперь соединим начало первого и конец второго. Это и есть сумма векторов и .

По тому же правилу можно сложить и несколько векторов. Пристраиваем их один за другим, а затем соединяем начало первого с концом последнего.

Представьте, что вы идете из пункта А в пункт В , из В в С , из С в D , затем в Е и в F . Конечный результат этих действий — перемещение из А в F .

При сложении векторов и получаем:

Видео:9 класс урок №2 Векторы и действия над нимиСкачать

Вычитание векторов

Вектор направлен противоположно вектору . Длины векторов и равны.

Теперь понятно, что такое вычитание векторов. Разность векторов и — это сумма вектора и вектора .

Видео:Физика | Ликбез по векторамСкачать

Умножение вектора на число

При умножении вектора на число k получается вектор, длина которого в k раз отличается от длины . Он сонаправлен с вектором , если k больше нуля, и направлен противоположно , если k меньше нуля.

Видео:Скалярные и векторные величины, основные определения.Скачать

Скалярное произведение векторов

Векторы можно умножать не только на числа, но и друг на друга.

Скалярным произведением векторов называется произведение длин векторов на косинус угла между ними.

Обратите внимание — перемножили два вектора, а получился скаляр, то есть число. Например, в физике механическая работа равна скалярному произведению двух векторов — силы и перемещения:

Если векторы перпендикулярны, их скалярное произведение равно нулю.
А вот так скалярное произведение выражается через координаты векторов и :

Из формулы для скалярного произведения можно найти угол между векторами:

Эта формула особенно удобна в стереометрии. Например, в задаче 14 Профильного ЕГЭ по математике нужно найти угол между скрещивающимися прямыми или между прямой и плоскостью. Часто векторным методом задача 14 решается в несколько раз быстрее, чем классическим.

В школьной программе по математике изучают только скалярное произведение векторов.
Оказывается, кроме скалярного, есть еще и векторное произведение, когда в результате умножения двух векторов получается вектор. Кто сдает ЕГЭ по физике, знает, что такое сила Лоренца и сила Ампера. В формулы для нахождения этих сил входят именно векторные произведения.

Векторы — полезнейший математический инструмент. В этом вы убедитесь на первом курсе.

Онлайн-курс «Математика 10+11 100 баллов»

— Теория: учебник Анны Малковой + 70 ч. видеоразборов.
— 144 ч. мастер-классов: 8 онлайн мастер-классов с Анной Малковой в месяц.
— Тренажер для отработки задач ЕГЭ (800+ задач): автоматическая + ручная проверки.
— Связь с Анной Малковой (чаты и почта).
— 9 репетиционных ЕГЭ: ежемесячно.
— Контроль: страница личных достижений учащегося, отчеты родителям.
— Личный кабинет.