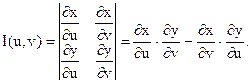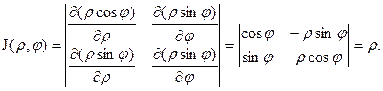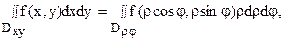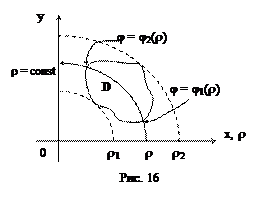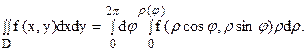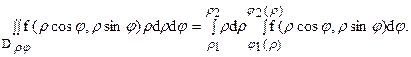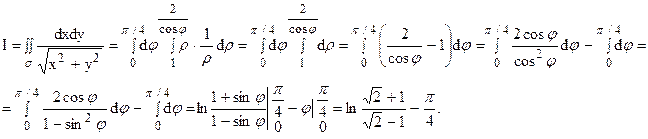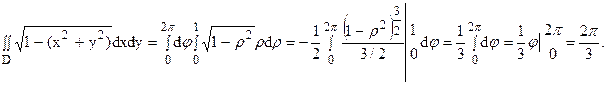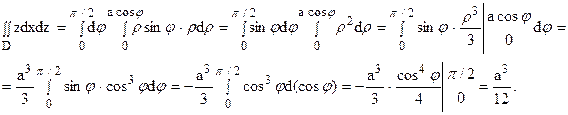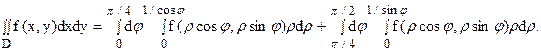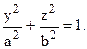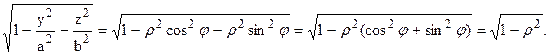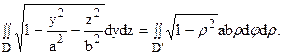- Что значит вычислить двойной интеграл в полярных координатах?
- Пределы интегрирования в повторных интегралах
- Случай первый
- Случай второй
- Случай третий
- Случай четвёртый
- Решения двойных интегралов в полярных координатах: примеры
- Вычислить двойной интеграл если область ограничена окружностью
- Контакты
- Замена переменных в двойном интеграле. Вычисление двойных интегралов в полярных координатах.
- 💥 Видео
Видео:Двойной интеграл в полярных координатахСкачать

Что значит вычислить двойной интеграл в полярных координатах?
Если область интегрирования представляет собой окружность или часть окружности, двойной интеграл проще вычислить не в декартовых прямоугольных координатах, а в полярных координатах. В этом случае подынтегральная функция выражается как функция полярных переменных r и φ с использованием соотношений между полярными и декартовыми координатами x = rcosφ и y = rsinφ :

Что представляет собой элемент площади dxdy , выраженный в полярных координатах? Для ответ на этот вопрос разделим область интегрирования D на участки линиями окружности r = const и лучами φ = const . Рассмотрим один частичный участок (заштрихованный на рисунке), который ограничивают лучи, образующие с полярной осью углы φ и φ + dφ и линии окружности с радиусом r и r + dr . Этот криволинейный четырёхугольник можем приближенно считать прямоугольником с длиной боковой стороны dr и длиной основания rdφ . Поэтому элемент площади в полярных координатах выражается следующим образом:
а двойной интеграл в полярных координатах записывается так:

Чтобы вычислить двойной интеграл в полярных координатах, его нужно выразить через повторные интегралы, так же, как и «обычный» двойной интеграл в декартовых прямоугольных координатах. В полярных координатах внешний интеграл всегда интегрируется по углу φ , а внутренний — по радиусу r .
Вычислить двойной интеграл в полярных координатах — значит, как и в декартовых прямоугольных координатах, найти число, равное площади упомянутой фигуры D .
Видео:Площадь фигуры через двойной интеграл в полярных координатахСкачать

Пределы интегрирования в повторных интегралах
При переходе от двойного интеграла в полярных координатах к повторным интегралам расстановку пределов интегрирования могут облегчить следующие закономерности.
Случай первый
Полюс O является внутренней точкой области интегрирования D , область ограничена линией r = r(φ) .
Тогда соответственно нижний и верхний пределы интегрирования внешнего интеграла равны 0 и 2π , а внутреннего интеграла — 0 и r(φ) . Переход к повторным интегралам осуществляется следующим образом:

Случай второй
Полюс O находится на границе области интегрирования D , ограниченного линией r = r(φ) , но не является угловой точкой.
Через полюс O проведём касательную. Пусть касательная образует с полярной осью угол α . Тогда соответственно нижний и верхний пределы интегрирования внешнего интеграла равны α и π + α , а внутреннего интеграла — 0 и r(φ) . Переход к повторным интегралам осуществляется следующим образом:

Случай третий
Полюс O находится на границе области интегрирования D , ограниченного линией r = r(φ) , и является угловой точкой.
Из полюса O проведём лучи, которые будут ограничивать область D . Пусть эти лучи образуют с полярной осью углы α и β . Тогда соответственно нижний и верхний пределы интегрирования внешнего интеграла равны α и β , а внутреннего интеграла — 0 и r(φ) . Переход к повторным интегралам осуществляется следующим образом:

Случай четвёртый
Полюс O находится вне области интегрирования D .
Из полюса O проведём лучи, которые будут ограничивать область D . Пусть эти лучи образуют с полярной осью углы α и β , а область D ограничивают линии r = r 1 (φ) и r = r 2 (φ) . Тогда соответственно нижний и верхний пределы интегрирования внешнего интеграла равны α и β , а внутреннего интеграла — r 1 (φ) и r 2 (φ) . Переход к повторным интегралам осуществляется следующим образом:

Видео:Двойной интеграл / Как находить двойной интеграл через повторный (двукратный) / Два способаСкачать
Решения двойных интегралов в полярных координатах: примеры
Пример 1. Вычислить в полярных координатах двойной интеграл

где область D ограничена линиями 


Решение. Строим на чертеже область интегрирования. Видим, что этот пример относится к третьему случаю из вышеописанных четырёх случаев расположения области интегрирования.
Выразим подынтегральную функцию как функцию полярных переменных:

Данные в условии линии, ограничивающие D , приводим к полярным координатам:
Переходим от двойного интеграла к повторному, учитывая пределы интегрирования, верные в третьем случае:

Вычисляем интеграл (так как повторные интегралы независимы друг от друга, каждый из них вычисляем отдельно и результаты перемножаем):
Пример 2. В повторном интеграле
перейти к полярной системе координат.
Решение. В повторном интеграле переменная x изменяется от -1 до 1, а переменная y — от параболы x² до 1. Таким образом, область интегрирования снизу ограничена параболой y = x² , а сверху — прямой y = 1 . Область интегирования изображена на следующем чертеже.
При переходе к полярным координатам область интегрирования нужно разделить на три части. Значит, данный повторный интеграл должен быть вычислен как сумма трёх интегралов. В первой области полярный радиус меняется от 0 до параболы, во второй области — от 0 до прямой y = 1 , в третьей области — от 0 до параболы. Точки пересечения прямой y = 1 и параболы: (1; 1) и (−1; 1) . В первой точке полярный угол составляет 




Запишем линии, ограничивающие область интегрирования в полярной системе координат. Найдём уравнение прямой y = 1 : 

Теперь у нас есть всё, чтобы от данного повторного интеграла перейти к полярным координатам:
Пример 3. Вычислить в полярных координатах двойной интеграл

где область D ограничена линией окружности 
Решение. Строим на чертеже область интегрирования.
Область интегрирования ограничивает линия окружности с центром в точке (a; 0) и радиусом a . В этом легко убедиться, преобразовав её уравнение следующим образом:

Линия окружности 




Напишем подынтегральную функцию в полярных координатах:

Теперь можем перейти в данном двойном интеграле к полярным координатам:
Наконец, находим двойной интеграл в полярных координатах:
В полученном выражении второе слагаемое равно нулю, так как и sinπ , и sin(−π) равны нулю. Продолжая, получаем:
Пример 4. Вычислить плоской фигуры, которую ограничивают линии 



Решение. Построим заданную фигуру на следующем рисунке.
Так как фигура является частью круга, её площадь проще вычислить в полярных координатах. Данные уравнения линий перепишем в полярных координатах:
Таким образом, у нас есть всё, чтобы записать площадь фигуры в виде двойного интеграл в полярных координатах, перейти к повторному интегралу и вычислить его:
Пример 5. Вычислить в полярных координатах двойной интеграл

где область D ограничена линиями 

Решение. Преобразуем данные уравнения линий, чтобы было проще построить чертёж:

Строим на чертеже область интегрирования.
В данных уравнениях линий перейдём к полярным координатам:

В данном двойном интеграле перейдём к полярным координатам, затем к повторным интегралам и вычислим интеграл:
Видео:Вычислить двойной интегралСкачать

Вычислить двойной интеграл если область ограничена окружностью
Учасники групи мають 10% знижку при замовленні робіт, і ще багато бонусів!
Контакты
 |
|
При вычислении двойных интегралов иногда бывает полезно сделать замену переменных. Пусть
|
функции, определенные на всей плоскости xOy или в некоторой ее области Dxy и имеющие непрерывные частные производные в области Dxy. Допустим также, что систему уравнений ( 7) можно однозначно разрешить относительно x и y:
Тогда каждой точке М(x;y) из области Dxy будет взаимно однозначно соответствовать пара чисел (u,v), называемых криволинейными координатами этой точки. Если область Dxy расположена в той части плоскости xOy, в которой введены криволинейные координаты u, v, то справедлива следующая формула:
|
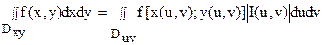
где Duv – область изменения криволинейных координат u и v, отвечающая области Dxy, а I(u,v) – якобиан преобразования ( 8):
|
Например, для полярных координат имеем:
В зависимости от строения области интегрирования или подынтегральной функции вычисление двойного интеграла может оказаться более простым не в прямоугольной, а в какой-нибудь из криволинейных систем координат. Наиболее распространенной из них является полярная.
Для того, чтобы преобразовать двойной интеграл в прямоугольных декартовых координатах в двойной интеграл в полярных координатах, нужно x и y в подынтегральной функции заменить соответственно через rcosj и rsinj, а выражение dxdy заменить выражением rdrdj:
|
где Drj – та же область Dху, но описанная в полярных координатах (поскольку в этом случае якобиан I = r).
В этой формуле следует обратить внимание на то, что в подынтегральной функции не только происходит замена координат по формулам перехода от декартовых к полярным, но и появляется дополнительный множитель r.
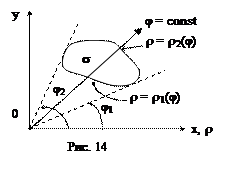
Пусть, например, внешнее интегрирование производится по j и область Dρφ является правильной в направлении j = сonst, т.е. каждый луч, выходящий из начала координат, пересекает область Dρφ по отрезку
(рис. 14).
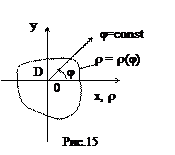
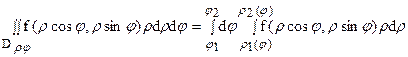
В частном случае, когда D содержит начало координат, имеем:
|
Если же внешнее интегрирование производится по r и область Dρφ является правильной в направлении
r = const, т.е. каждая окружность пересекает, имея центром начало координат, область Dρφ по дуге этой окружности (только в двух точках) (см. рис.16), то справедлива формула:
|
Пример 12.
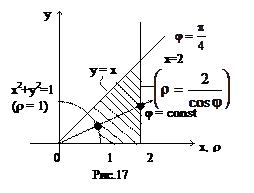
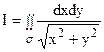
Хотя данный интеграл можно вычислить в прямоугольной декартовой системе координат, в которой он задан, но неопределенные интегралы, которые при этом возникнут, достаточно сложны.
Перейдем к полярной системе координат. Вспомним, что 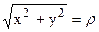
Таким образом, искомый интеграл можно представить в виде:
Пример 13.
Вычислить двойной интеграл 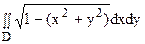
Область D есть круг радиуса 1 с центром в начале координат. Введем полярные координаты. В полярных координатах x 2 + y 2 = r 2 и уравнение окружности принимает вид r = 1.
Тогда по формуле ( 13) получаем:
Пример 14.
Вычислить двойной интеграл 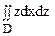
Область D – полукруг. Введем полярные координаты: x = rcosj, z = rsinj.
Уравнение окружности в полярных координатах принимает вид r 2 = racosj, или r = acosj.
Подынтегральная функция имеет вид z = rsinj. Угол j меняется от 0 до p/2 (полукруг находится в I четверти). При каждом фиксированном значении угла j r меняется от 0 (в начале координат) до r = acosj (на окружности). Тогда получаем:
Пример 15.
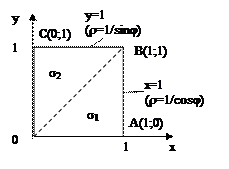
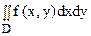
Уравнение стороны АВ (х = 1) в полярных координатах принимает вид rcosj = 1, или r = 1/cosj, а ВС будет r = 1/sinj. Угол j меняется от 0 до p/2 (квадрат находится в I четверти). При изменении угла от 0 до p/4 r меняется от 0 до r = 1/cosj, а при изменении угла от p/4 до p/2 r меняется от 0до r = 1/sinj.
Пример 16.
Вычислить двойной интеграл 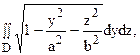
Для решения этой задачи удобно ввести так называемые обобщенные полярные координаты, положив y = arcosj, z = brsinj.
Найдем якобиан данного преобразования:
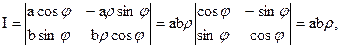
Подынтегральная функция принимает вид:
Угол j меняется от 0 до 2p. Уравнение эллипса принимает вид r = 1, поэтому r меняется от 0 до 1. И тогда
💥 Видео
Двойной интеграл (ч.25). Вычисление в полярных координатах. Высшая математика.Скачать

Вычислить двойной интеграл по области, ограниченной линиями ∫∫(5x+y)dxdy D: y=x^3, y=0, x=3.Скачать

Математический анализ, 41 урок, Вычисление двойных интеграловСкачать

Двойной интеграл. Правильные области, вычислениеСкачать

Математика без ху!ни. Двойной интеграл, вычисление двумя способами.Скачать
Изменение порядка интегрирования в повторном интегралеСкачать

Вычислить двойной интеграл по областиСкачать

Двойной интеграл. Вычисление в полярных координатахСкачать

Математика Без Ху!ни. Полярные координаты. Построение графика функции.Скачать

Вычислить двойной интеграл ★ Замена переменных в двойном интегралеСкачать

Вычисление двойного интегралаСкачать
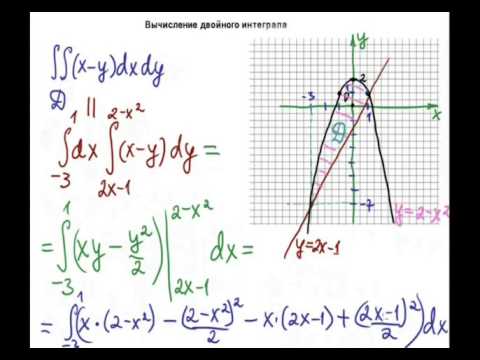
Математика без ху!ни. Двойные интегралы. Часть1. Как вычислять.Скачать

Двойной интеграл (ч. 27). Вычисление в полярных координатах. Высшая математика.Скачать

Вычисление двойных интегралов в ПСК (полярной системе координат). Примеры.Скачать

Математика без Ху!ни. Определенные интегралы, часть 3. Площадь фигуры.Скачать