Данная разработка — подробный разбор нескольких обучающих задач на применение векторов к задачам на доказательство, содержит доказательство теоремы о средней линии трапеции. Презентация может быть использована на уроках геометрии в 8 классе, либо в 9 классе в зависимости от календарно-тематического планирования (учебник Геометрия 7-9, автор Л.С.Атанасян)
Просмотр содержимого документа
«Применение векторов к решению задач»
Применение векторов к решению задач
К учебнику Геометрия 7-9,
автор Л.С.Атанасян и др.
Автор: Софронова Наталия Андреевна,
учитель математики высшей категории
МОУ «Упшинская основная общеобразовательная школа»
Оршанского района Республики Марий Эл
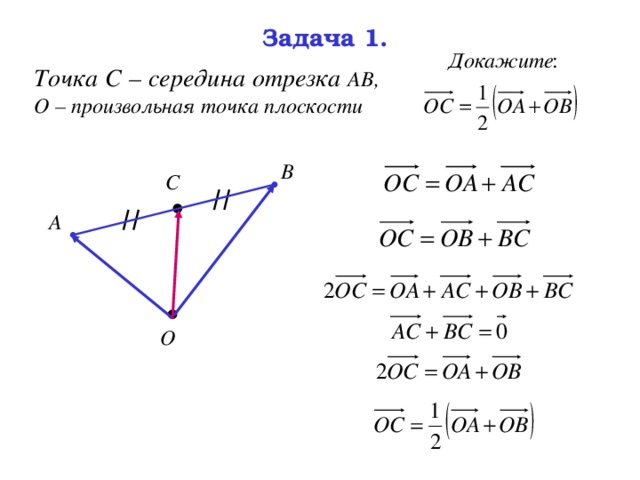
Точка С – середина отрезка АВ, О – произвольная точка плоскости
Доказать, что прямая, проведенная через середины оснований трапеции проходит через точку пересечения продолжений боковых сторон.
В треугольнике АВС В 1 — середина стороны АС, точка А 1 лежит на стороне ВС так, что ВА 1 : А 1 С = 1 : 2. Используя векторы, докажите, что середина ВВ 1 лежит на прямой АА 1.
Доказать: О є АА 1
О – середина ВВ 1
Задача 3 (продолжение).
О – середина ВВ 1
Доказать: О є АА 1
лежат на одной прямой,
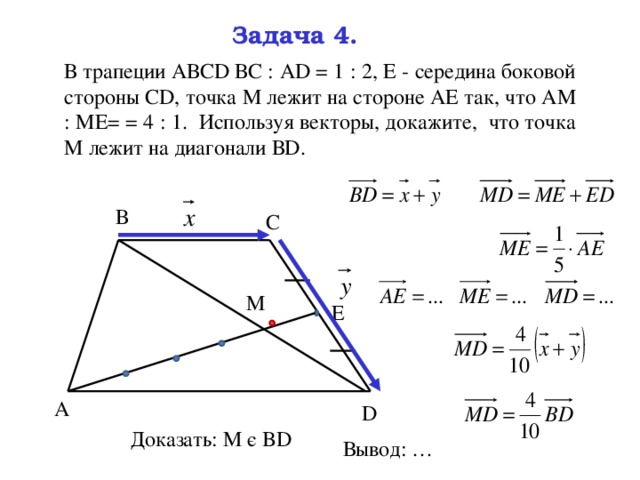
В трапеции АВСD ВС : АD = 1 : 2, Е — середина боковой стороны СD, точка М лежит на стороне АЕ так, что АМ : МЕ= = 4 : 1. Используя векторы, докажите, что точка М лежит на диагонали ВD.
Доказать: М є BD
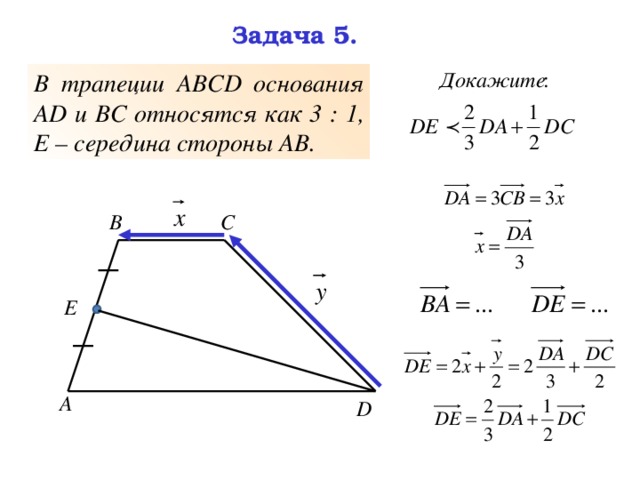
В трапеции АВСD основания АD и ВС относятся как 3 : 1, Е – середина стороны АВ.
Задача 5 (продолжение).
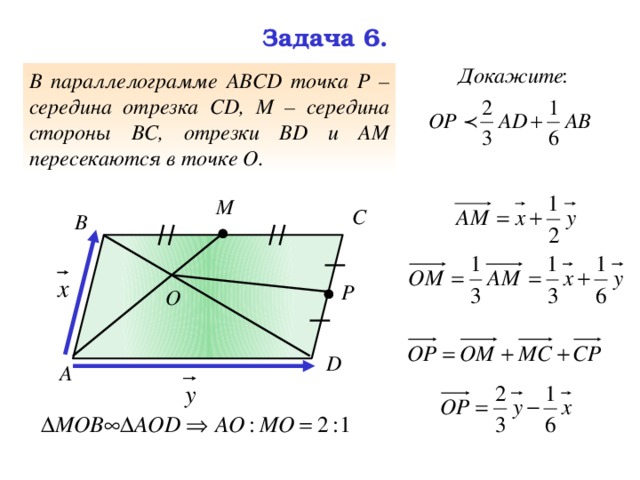
В параллелограмме АВСD точка Р – середина отрезка СD, М – середина стороны ВС, отрезки ВD и АМ пересекаются в точке О.
Задача 6 (продолжение).
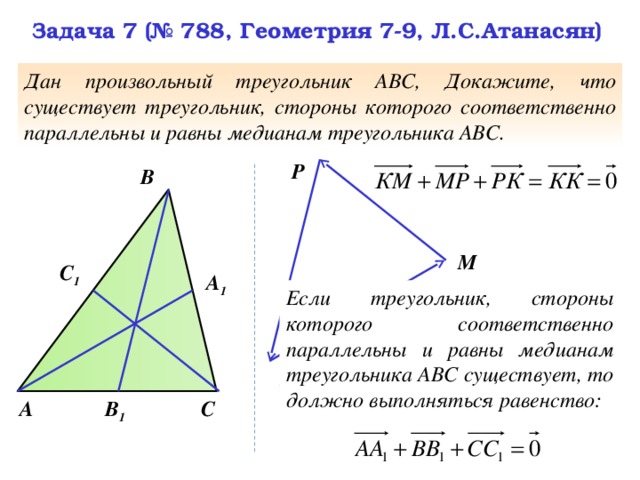
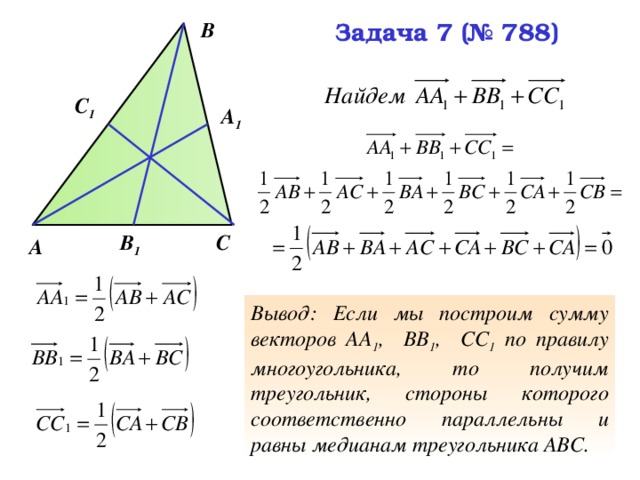
Задача 7 (№ 788, Геометрия 7-9, Л.С.Атанасян)
Дан произвольный треугольник АВС, Докажите, что существует треугольник, стороны которого соответственно параллельны и равны медианам треугольника АВС.
Если треугольник, стороны которого соответственно параллельны и равны медианам треугольника АВС существует, то должно выполняться равенство:
Вывод: Если мы построим сумму векторов АА 1 , ВВ 1 , СС 1 по правилу многоугольника, то получим треугольник, стороны которого соответственно параллельны и равны медианам треугольника АВС.
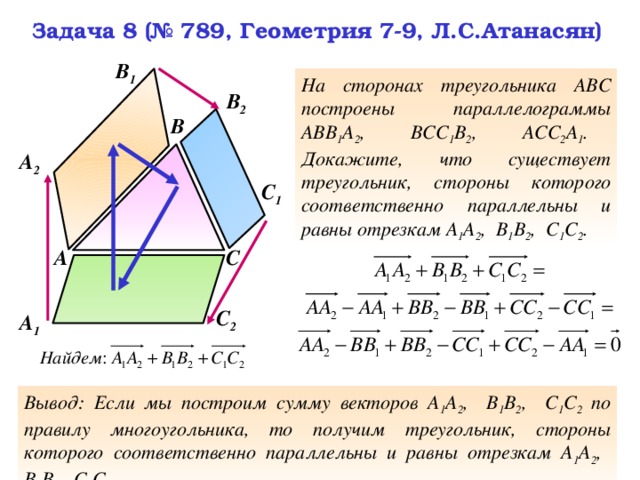
Задача 8 (№ 789, Геометрия 7-9, Л.С.Атанасян)
На сторонах треугольника АВС построены параллелограммы АВВ 1 А 2 , ВСС 1 В 2 , АСС 2 А 1 . Докажите, что существует треугольник, стороны которого соответственно параллельны и равны отрезкам А 1 А 2 , В 1 В 2 , С 1 С 2 .
Вывод: Если мы построим сумму векторов А 1 А 2 , В 1 В 2 , С 1 С 2 по правилу многоугольника, то получим треугольник, стороны которого соответственно параллельны и равны отрезкам А 1 А 2 , В 1 В 2 , С 1 С 2 .
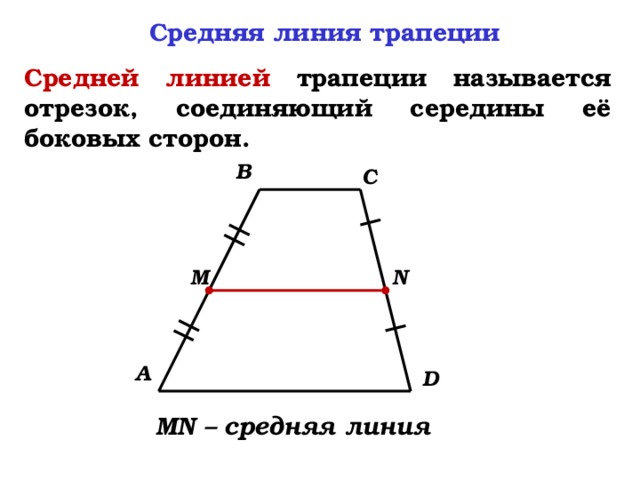
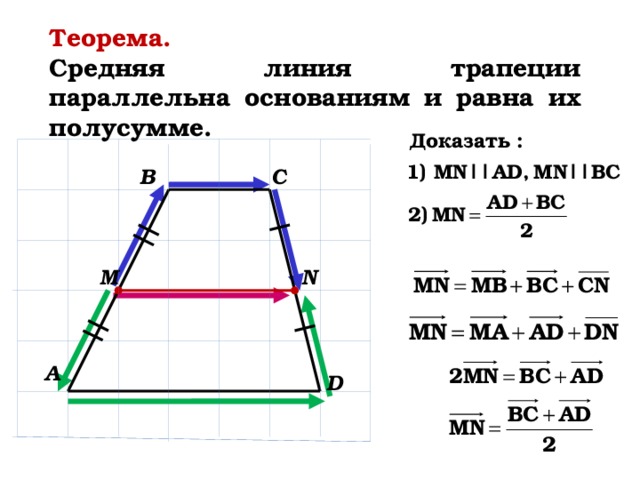
Средняя линия трапеции
Средней линией трапеции называется отрезок, соединяющий середины её боковых сторон.
Средняя линия трапеции параллельна основаниям и равна их полусумме.
Видео:8 класс, 48 урок, Применение векторов к решению задачСкачать
Разработка урока по теме «Применение векторов к решению задач. Средняя линия трапеции».
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Видео:умножение ВЕКТОРА на число + теорема о средней линии ТРАПЕЦИИСкачать
«Управление общеобразовательной организацией:
новые тенденции и современные технологии»
Свидетельство и скидка на обучение каждому участнику
Г – 9 класс Урок № 7
Тема: «Применение векторов к решению задач. Средняя линия трапеции».
Дидактическая: на конкретных примерах показать применение векторов при решении геометрических задач; ввести понятия средней линии трапеции; доказать теорему о средней линии трапеции с помощью векторов.
Развивающая: развивать логическое мышление учащихся, учить решать задачи; развивать воображение – репродуктивное, творческое, образное; абстрактное мышление, умение обобщать.
Воспитательная: нравственное воздействие, воспитание культуры умственного труда, культуры общения.
Знать, действия производимые с векторами, понятие средней линии трапеции, теорему о средней линии трапеции.
Уметь вычислять среднюю линию трапеции, решать задачи с помощью векторов.
Сообщение темы и целей урока.
Актуализация знаний и умений обучающихся.
Проверка выполнения домашнего задания. Разбор нерешенных заданий.
Повторение изученного материала.
1. Ответить на вопросы на с. 213–214.
2. Проверка усвоения учащимися материала.
1. Устно ответить на вопросы:
1) Какие векторы называются коллинеарными? Изобразите на рисунке сонаправленные векторы 
и 
и противоположно направленные векторы 
и .
2) Какой вектор называется произведением данного вектора на данное число?
3) Могут ли векторы и 
быть неколлинеарными?
4) Сформулируйте основные свойства умножения вектора на число.
2. Решить задачу на доске и в тетрадях по готовому чертежу:
Точки M и N лежат соответственно на сторонах AD и BC четырехугольника ABCD, причем AM : MD = BN : NC = 3 : 4.
Докажите, что середины отрезков AB, MN и CD лежат на одной прямой.
Пусть K1 – середина AB, K2 – середина MN, K3 – середина CD. Согласно задаче 2 из п. 84 имеем 
. Из условия следует, что 
, поэтому 
.
Таким образом, векторы 
и 
коллинеарные, и, значит, точки K1, K2 и K3 лежат на одной прямой.
Изучение нового материала.
1. Определение трапеции. Виды трапеций.
2. Определение средней линии трапеции.
3. Доказательство теоремы о средней линии трапеции.
Доказательство оформить на доске и в тетрадях в виде следующей краткой записи:
Дано: ABCD – трапеция, AD || BC, M – середина стороны AB; N – середина стороны CD (рис. 266 учебника).
Доказать: MN || AD, MN = 
.
1) Согласно рассмотренной в классе задаче 1 
.
2) Так как 
, то 
и, значит, MN || AD.
3) Так как , то 
= AD + BC, поэтому MN = 
(AD + BC).
Формирование умений и навыков.
Работа по учебнику.
1. Векторы могут использоваться для решения геометрических задач. Рассмотрим вспомогательную задачу.
2. Разобрать решение задачи 1 на с. 208 учебника по рис. 264.
3. Решить задачу 2. Точки M и N – середины сторон AB и CD четырехугольника ABCD. Докажите, что 
Пусть О – произвольная точка. Согласно задаче 1 из п. 84 имеем 
поэтому 
.
Примечание. Результат задачи 2 можно использовать при доказательстве теоремы о средней линии трапеции на следующем уроке.
4. 1. Решить на доске и в тетрадях задачу № 793.
Пусть a и b – основания трапеции, тогда а + b = 48 – (13 + 15) = 20 (см); средняя линия MN = 
= 10 (см).
2. Решить задачу № 795.
3. Решить задачу № 799 на доске и в тетрадях.
Пусть BK – перпендикуляр, проведенный к основанию AD данной трапеции.
Тогда KD = AD – AK.
Но AK = 
, поэтому KD = AD – 
, то есть отрезок KD равен средней линии трапеции. Значит, средняя линия трапеции равна 7 см.
5. Решить задачу 3. Точка С лежит на отрезке AB, причем АС : СВ = 2 : 3. Докажите, что для любой точки О справедливо равенство 
По условию AC:CB=2 : 3,поэтому 
Но 
Следовательно, 
откуда получается
Примечание. Задача 3 является частным случаем более общей задачи 806.
6. Решить задачу № 786 на доске и в тетрадях.
Так как точка А1 – середина стороны ВС, то 
.
Далее 
7. При наличии времени решить задачу 4.
Точки K, L, M, N – середины сторон AB, BC, CD, DE пятиугольника ABCDE, а точки P и Q – середины отрезков KM и LN. Докажите, что PQ || AE и PQ = 1/4 AE.
Пусть О – произвольная точка. Согласно задаче 1 из п. 84 
. Аналогично, 
.
Из этих равенств следует, что 
Отсюда следует, что PQ || AE и PQ = 
AE.
Подвести итоги урока, выставить отметки обучающимся за урок.
В результате изучения параграфа обучающиеся должны знать, какой вектор называется произведением вектора на число; уметь формулировать свойства умножения вектора на число; знать, какой отрезок называется средней линией трапеции; уметь формулировать и доказывать теорему о средней линии трапеции; уметь решать задачи типа №№ 782–787; 793–799.
Домашнее задание: изучить материал п. 87, 88; ответить на вопросы 18–20, с. 214 учебника; решить задачи №№ 787, 794, 796.
Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать
Применение векторов к решению задач (продолжение)
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
На данном уроке мы рассмотрим применение векторов для решения различных геометрических задач, вспомним и докажем некоторые геометрические факты.
Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок «Векторы и координаты»
📸 Видео
Геометрия 9 класс. Средняя линия трапецииСкачать
Трапеция. Практическая часть - решение задачи. 8 класс.Скачать
Геометрия 9 класс (Урок№5 - Средняя линия трапеции.)Скачать
8 класс, 49 урок, Средняя линия трапецииСкачать
Выразить векторы. Разложить векторы. Задачи по рисункам. ГеометрияСкачать
87. Применение векторов к решению задачСкачать
ВЕКТОРЫ решение задач 9 класс АтанасянСкачать
Как выражать вектор? Как решать задачу с вектором? | TutorOnlineСкачать
ВЕКТОРЫ 9 класс С НУЛЯ | Математика ОГЭ 2023 | УмскулСкачать
ТРАПЕЦИЯ теорема о средней линии Атанасян 9 классСкачать
Трапеция, решение задач. Вебинар | МатематикаСкачать
ТРАПЕЦИЯ — Что такое трапеция, Виды Трапеций, Площадь Трапеции // Геометрия 8 классСкачать
18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать
№746. Основание AD прямоугольной трапеции ABCD с прямым углом A равно 12 смСкачать
Средняя линия треугольника и трапеции. 8 класс.Скачать
Произведение вектора на число. Средняя линия трапеции. Урок 3. Геометрия 9 классСкачать
№346. Точки М и N — середины оснований АВ и CD трапеции ABCD, а О — произвольнаяСкачать
