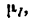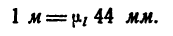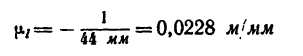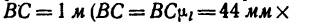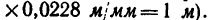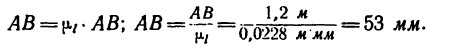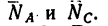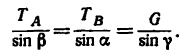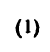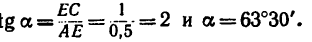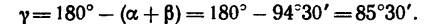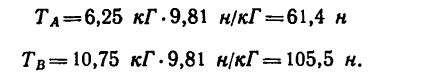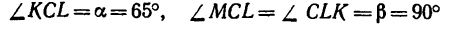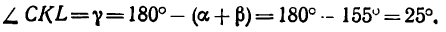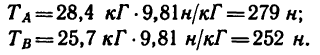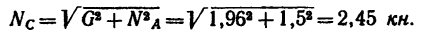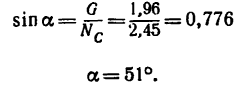При воздействии на одно тело нескольких сил одновременно тело начинает двигаться с ускорением, являющимся векторной суммой ускорений, которые бы возникли под воздействием каждой силы по отдельности. К действующим на тело силам, приложенным к одной точке, применяется правило сложения векторов.
Векторная сумма всех сил, одновременно воздействующих на тело, это сила равнодействующая, которая определяется по правилу векторного сложения сил:
R → = F 1 → + F 2 → + F 3 → + . . . + F n → = ∑ i = 1 n F i → .
Равнодействующая сила действует на тело также, как и сумма всех действующих на него сил.
Видео:9 класс, 1 урок, Разложение вектора по двум неколлинеарным векторамСкачать

Правило параллелограмма и правило многоугольника
Для сложения 2 -х сил используют правило параллелограмма (рисунок 1 ).
Рисунок 1 . Сложение 2 -х сил по правилу параллелограмма
Выведем формулу модуля равнодействующей силы с помощью теоремы косинусов:
R → = F 1 → 2 + F 2 → 2 + 2 F 1 → 2 F 2 → 2 cos α
При необходимости сложения более 2 -х сил используют правило многоугольника: от конца
1 -й силы необходимо провести вектор, равный и параллельный 2 -й силе; от конца 2 -й силы необходимо провести вектор, равный и параллельный 3 -й силе и т.д.
Рисунок 2 . Сложение сил правилом многоугольника
Конечный вектор, проведенный от точки приложения сил в конец последней силы, по величине и направлению равняется равнодействующей силе. Рисунок 2 наглядно иллюстрирует пример нахождения равнодействующей сил из 4 -х сил: F 1 → , F 2 → , F 3 → , F 4 → . Причем суммируемые векторы совсем необязательно должны быть в одной плоскости.
Результат действия силы на материальную точку будет зависеть только от ее модуля и направления. У твердого тела есть определенные размеры. Потому силы с одинаковыми модулями и направлениями вызывают разные движения твердого тела в зависимости от точки приложения.
Линией действия силы называют прямую, проходящую через вектор силы.
Рисунок 3 . Сложение сил, приложенных к различным точкам тела
Если силы приложены к различным точкам тела и действуют не параллельно по отношению друг к другу, тогда равнодействующая приложена к точке пересечения линий действия сил (рисунок 3 ). Точка будет находиться в равновесии, если векторная сумма всех сил, действующих на нее, равняется 0 : ∑ i = 1 n F i → = 0 → . В данном случае равняется 0 и сумма проекций данных сил на любую координатную ось.
Видео:Разложение вектора по базису. 9 класс.Скачать

Разложение вектора силы по направлениям
Разложение сил на две составляющие – это замена одной силы 2 -мя, приложенными в той же точке и производящими на тело такое же действие, как и эта одна сила. Разложение сил осуществляется, как и сложение, правилом параллелограмма.
Задача разложения одной силы (модуль и направление которой заданы) на 2 , приложенные в одной точке и действующие под углом друг к другу, имеет однозначное решение в следующих случаях, когда известны:
- направления 2 -х составляющих сил;
- модуль и направление одной из составляющих сил;
- модули 2 -х составляющих сил.
Пример 1
Необходимо разложить силу F на 2 составляющие, находящиеся в одной плоскости с F и направленные вдоль прямых a и b (рисунок 4 ). Тогда достаточно от конца вектора F провести 2 прямые, параллельные прямым a и b . Отрезок F A и отрезок F B изображают искомые силы.
Рисунок 4 . Разложение вектора силы по направлениям
Второй вариант данной задачи – найти одну из проекций вектора силы по заданным векторам силы и 2 -й проекции (рисунок 5 а ).
Рисунок 5 . Нахождение проекции вектора силы по заданным векторам
Во втором варианте задачи необходимо построить параллелограмм по диагонали и одной из сторон, как в планиметрии. На рисунке 5 б изображен такой параллелограмм и обозначена искомая составляющая F 2 → силы F → .
Итак, 2 -й способ решения: прибавим к силе силу, равную — F 1 → (рисунок 5 в ). В итоге получаем искомую силу F → .
Три силы F 1 → = 1 Н ; F 2 → = 2 Н ; F 3 → = 3 Н приложены к одной точке, находятся в одной плоскости (рисунок 6 а ) и составляют углы с горизонталью α = 0 ° ; β = 60 ° ; γ = 30 ° соответственно. Необходимо найти равнодействующую силу.
Решение
Рисунок 6 . Нахождение равнодействующей силы по заданным векторам
Нарисуем взаимно перпендикулярные оси О Х и O Y таким образом, чтобы ось О Х совпадала с горизонталью, вдоль которой направлена сила F 1 → . Сделаем проекцию данных сил на координатные оси (рисунок 6 б ). Проекции F 2 y и F 2 x отрицательны. Сумма проекций сил на координатную ось О Х равняется проекции на данную ось равнодействующей: F 1 + F 2 cos β — F 3 cos γ = F x = 4 — 3 3 2 ≈ — 0 , 6 Н .
Точно также для проекций на ось O Y : — F 2 sin β + F 3 sin γ = F y = 3 — 2 3 2 ≈ — 0 , 2 Н .
Модуль равнодействующей определим с помощью теоремы Пифагора:
F = F x 2 + F y 2 = 0 , 36 + 0 , 04 ≈ 0 , 64 Н .
Направление равнодействующей найдем при помощи угла между равнодействующей и осью (рисунок 6 в ):
t g φ = F y F x = 3 — 2 3 4 — 3 3 ≈ 0 , 4 .
Сила F = 1 к Н приложена в точке В кронштейна и направлена вертикально вниз (рисунок 7 а ). Необходимо найти составляющие данной силы по направлениям стержней кронштейна. Все необходимые данные отображены на рисунке.
Решение
Рисунок 7 . Нахождение составляющих силы F по направлениям стержней кронштейна
Дано:
F = 1 к Н = 1000 Н
Пускай стержни прикручены к стене в точках А и С . На рисунке 7 б изображено разложение силы F → на составляющие вдоль направлений А В и В С . Отсюда понятно, что
F 1 → = F t g β ≈ 577 Н ;
F 2 → = F cos β ≈ 1155 Н .
Ответ: F 1 → = 557 Н ; F 2 → = 1155 Н .
Видео:Найдите разложение вектора по векторам (базису)Скачать

Разложение силы на две составляющие в теоретической механике
Разложение силы на две составляющие:
Решение многих практических задач по статике сводится к разложению силы на две составляющие. Подобные задачи решаются либо по правилу параллелограмма, либо по правилу треугольника и, в зависимости от исходных данных, приводятся к одному из четырех типов.
Общая методика решения приведенных ниже задач сводится к следующему:
- Выбираем метод решения — графический или графо-аналитический.
- Выбираем правило, по которому будем решать задачу, т. е. либо правило параллелограмма, либо правило треугольника.
- Если выбран графический метод, то далее выбираем масштаб построения, строим параллелограмм или треугольник (в соответствии с выбранным правилом) и, наконец, измеряем стороны получившейся фигуры, находим модули соответствующих сил, а измерив углы, найдем их направления.
- Если выбран графо-аналитический метод, то в зависимости от избранного правила строим параллелограмм или треугольник, соблюдая приблизительные соотношения размеров длин и углов, а затем, в зависимости от исходных данных, используем геометрические или тригонометрические соотношения.
Задача №1
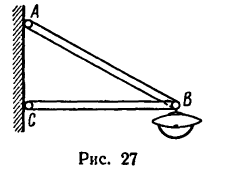
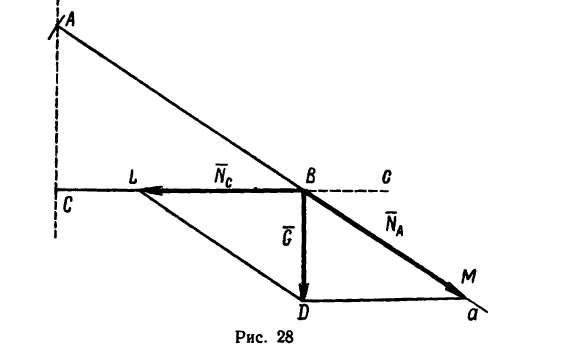
Фонарь весом 80 н подвешен на кронштейне АВС, укрепленном на вертикальной стене (рис. 27). Определить усилия, возникшие в горизонтальном стержне СВ и наклонной тяге АВ после подвески фонаря, если СВ = 1 ли /AB = 1,2 л. Соединения в точках А, В и С кронштейна — шарнирные.
Решение 1—графическим методом по правилу параллелограмма.
1. Если избран графический метод решения, то прежде всего необходимо в масштабе построить кронштейн АВС. Выполнение чертежа кронштейна сводится, как это следует из формы и размеров, заданных в условии задачи, к построению прямоугольного треугольника по двум заданным сторонам.
2. Построим кронштейн в масштабе «1 м в 44 мм». Обозначив масштаб чертежа
Отсюда масштаб построения кронштейна
3. Из произвольной точки С (рис. 28) проводим горизонтальную и вертикальную линии. На горизонтальной линии отложим
отрезок ВС = 44 мм, который в выбранном масштабе и изобразит горизонтальный стержень кронштейна
Длина отрезка АВ, который изобразит тягу АВ, определяется из равенства
Найденную длину АВ = 53 мм отложим при помощи циркуля из точки В так, чтобы получить точку А на вертикали, проведенной ранее из точки С. Построенный треугольник АВС изображает данный в условии задачи кронштейн.
4. Строим параллелограмм сил, действующих на точку В кронштейна.
Вес фонаря G = 80 н, действующий на кронштейн вертикально вниз, изобразим отрезком BD=20 мм. Значит масштаб построения
для сил 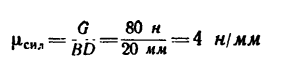
(4 н в 1 мм).
Благодаря тому что в точках А, В и С кронштейна соединения шарнирные, стержни, находясь под действием веса фонаря, либо растягиваются, либо сжимаются. Иными словами, искомые усилия действуют вдоль стержней. Значит направления сил известны (1-й тип задачи на разложения силы по правилу параллелограмма).
Изобразим направление действия искомых сил линиями Аа и Сс, пересекающимися в точке В — точке приложения к кронштейну веса фонаря.
Из точки D (конца вектора 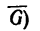
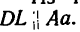
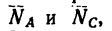
5. При помощи масштабной линейки измерим отрезки ВМ и BL:
ВМ=36 мм и BL—30 мм.
Следовательно, 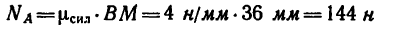
и 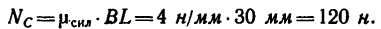
Как видно из получившегося на рис. 28 построения, тяга АВ кронштейна растягивается силой, равной 144 н, а стержень ВС сжимается силой 120 н.
Решение 2—графо-аналитическим методом по правилу параллелограмма с использованием геометрических соотношений.
1. Используя рис. 27, на котором изображен кронштейн, строим параллелограмм сил. Через произвольную точку а (рис. 29) проводим прямые 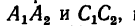
Из той же точки а откладываем вертикально вниз отрезок ab, который изображает силу 
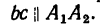
2. Теперь имеются две геометрические фигуры — треугольник АВС (см. рис. 27), изображающий заданный кронштейн, и силовой параллелограмм (см. рис. 29).
Геометрически 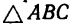
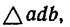
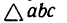
Используя свойство подобных треугольников (замечаем, что db = ac—Nc), получаем
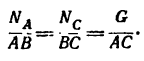
3. Решая получившиеся пропорции, находим 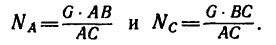
Неизвестную в кронштейне длину АС найдем по теореме Пнфагора (из условия задачи ясно, что угол АСВ — прямой)
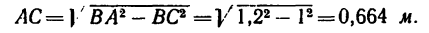
Подставляя в выражения для 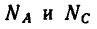
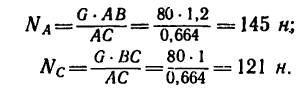
Таким образом, результат практически тот же, что и при графическом решении. Некоторое расхождение объясняется меньшей точностью графического решения.
Как уже известно, графо-аналитическое решение задачи 22-6 основано на подобии двух треугольников: кронштейна, имеющего вид треугольника, и силового треугольника. Но возможен случай, когда на чертеже нагруженного устройства или конструкции не будет треугольника, подобного силовому. Тогда для решения задачи целесообразно применить графо-аналитический метод с использованием тригонометрических соотношений.
Рассмотрим такую задачу.
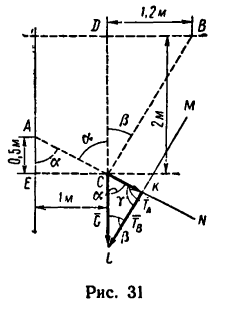
Задача №2
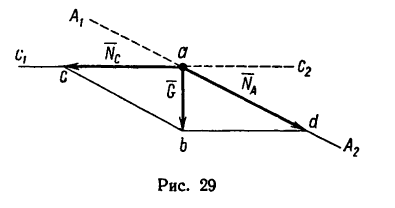
При помощи двух нерастяжимых нитей АС и ВС удерживается груз, вес которого 12 кГ. Положение нитей и груза показано на рис. 30. Определить натяжение нитей.
Решение 1 — графо-аналитическим методом по правилу треугольника с использованием тригонометрии.
1. Так же, как и в предыдущей задаче, необходимо силу G=12 кГ разложить на две составляющие, линии действия которых совпадают с направлениями линий АС и ВС.
2. Изобразим силу 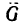
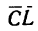
3. Если в треугольнике CKL известны углы а, 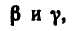
4. Из построения силового треугольника следует, что 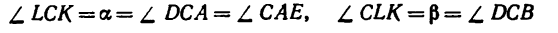
(для наглядности положение нитей относительно вектора G показано на рис. 31 штриховой линией). А так как треугольники 


Из 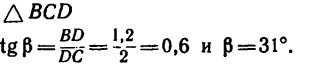
Угол у легко найдем как дополнение к 
5. И теперь, зная углы а, 
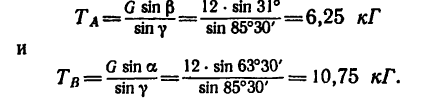
Таким образом, нить С А растягивается усилием, равным 6,25 кГ, а нить СВ — усилием 10,75 кГ.
Если эти усилия выразить в единицах СИ, то
и
Задачу просто решить графическим методом. Для этого нужно начертить в масштабе расположение нитей и, выбрав масштаб для сил (например, 0,2 кГ/мм), построить на векторе G силовой треугольник и, измерив его стороны, найти
Графо-аналитический метод с использованием свойств подобных треугольников целесообразно применять к решению таких задач в том случае, если в схеме конструкции или устройства имеется треугольник, подобный силовому.
Если же в схеме конструкции нет треугольника, подобного силовому, то решение графо-аналитическим методом целесообразнее производить с использованием тригонометрических свойств, потому что при наличии линейных размеров необходимые для решения задачи значения углов, как правило, найти очень просто.
Необходимо отметить, что в задачах, подобных 22-6 и 23-6, усилия, вызываемые нагрузкой в стержнях кронштейнов или нитях устройств, удерживающих груз, не зависят от длины этих нитей или стержней.
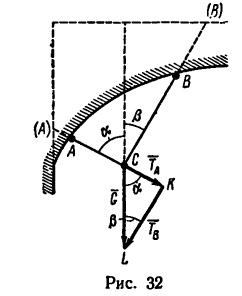
Допустим, что груз (задача 23-6) удерживается нитями, прикрепленными не к вертикальной стенке и горизонтальному потолку, как на рис, 30, а к двум точкам криволинейной (сводчатой) поверхности (рис. 32). Но если при этом углы аи
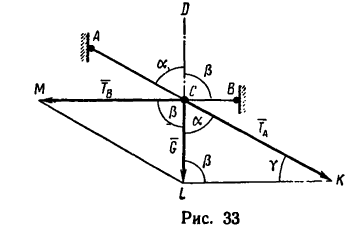
Задача №3
Груз весом G= 12 кГ удерживается при помощи двух нитей, которые образуют с вертикалью (линией действия веса G) углы а=65° и 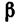
Решение—графо-аналитическим методом по правилу параллелограмма.
1. Исходя из условия задачи, построим чертеж (рис. 33). Из точки С проводим вертикальный отрезок CL, изображающий вектор 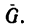
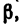
2. Вектор 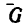
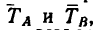
3. На основе построения параллелограмма CKLM очень просто определяются его углы:
4. Так как силовой параллелограмм делится на два прямоугольных треугольника, то легко найти оба усилия: 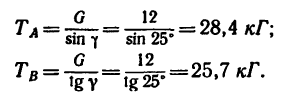
единицах СИ усилия равны:
Задачи 6 относятся к первому типу задач на разложение силы по правилу параллелограмма или треугольника.
Рассмотрим теперь по одной задаче второго (задача 25-6), третьего (задача 26-6) и четвертого (задача 27-6) типов.
Задача №4
Груз массой 200 кг необходимо подвесить на кронштейне, у которого один из стержней горизонтальный и в нем должно возникнуть сжимающее усилие не более 1,5 кн.
Как нужно расположить второй стержень, чтобы в нем возникло растягивающее усилие? Определить величину этого усилия.
Эта задача аналогична задаче 8-2, которая решена графическим методом, поэтому графическое решение здесь не приводим.
Решение —графо-аналитическим методом по правилу треугольника.
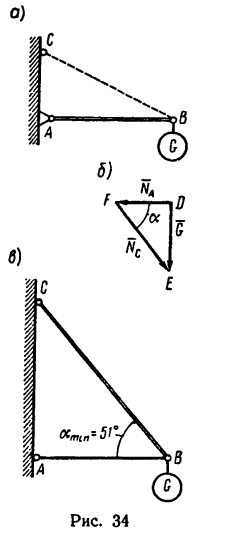
1. Изобразим (рис. 34, а) стержень АВ в горизонтальном положении, т. е. в том, какое он должен занимать по условию, и допустим, что к концу В стержня приложена нагрузка 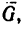
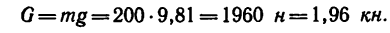
Известно, что этот стержень должен испытывать сжимающее усилие 1,5 кн. Поэтому сила, приложенная к стержню в точке В, будет направлена от В к А. Обозначим эту силу
Расположение стержня ВС кронштейна неизвестно и поэтому он условно показан штриховой линией.
2. Строим силовой треугольник (рис. 34, б). Из произвольной точки D отложим вертикальный отрезок DE, изображающий вес груза 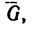
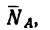
Для того чтобы найти второе слагаемое вектора 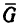
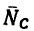
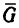
Чтобы выполнить это действие по правилу треугольника, соединим точки F и Е. Сторона FE получившегося треугольника изображает искомое усилие 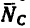
3. Треугольник DEF прямоугольный, поэтому
Если мысленно в точку В кронштейна перенести силу 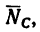
Угол АВС (рис. 34, в) между стержнями должен быть равен углу между линиями действия сил 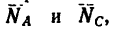
и
Таким образом, если в кронштейне стержень ВС расположить к горизонтальному стержню В А под углом а=51°, то груз весом G = l,96 кн, действующий на точку В кронштейна, вызовет в стержне В А сжимающее усилие 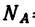
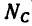
Если при изготовлении кронштейна увеличить угол a(a>51°), то уменьшится нагрузка на оба стержня, причем при вертикальном положении стержня ВС (а = 90°) усилие 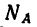
Если же при изготовлении кронштейна угол а уменьшить (а 51° или а
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:РАЗЛОЖЕНИЕ ВЕКТОРА ПО ДВУМ неколлинеарным ВЕКТОРАМ 9 классСкачать

Разложение вектора
Разложение вектора а на составляющие — операция замены вектора а несколькими другими векторами аь а2, а3 и т. д., которые при их сложении образуют начальный вектор а; в этом случае векторы db а2, а3 и т. д. называются составляющими вектора а. Иными словами, разложение любого вектора на составляющие — действие, обратное сложению векторов.
Из рис. 1.5 следует, что сумма векторов ах и ау равна начальному вектору а, т. е. d = ах + ау; здесь ах и ау являются составляющими вектора ау вдоль осей Ох и Оу соответственно.
Проекция вектора d на ось Ох — длина вектора ах (величина алгебраическая), взятая со знаком «минус» или «плюс». Аналогично вводится понятие проекций вектора d на заданную координатную ось Оу.
При нахождении проекций вектора а предварительно находят его составляющие ах и ау по осям; если составляющая (ах, ау) совпадает с положительным направлением оси, проекцию берут со знаком «плюс», если же нет, то со знаком «минус». Величина проекций определяются по формулам
где а — модуль вектора ау; а и р — углы между положительным направлением соответствующей оси и вектора ау (рис. 1.5).
Длина (модуль) вектора а равна а = ^а 2 х + а 2 у, а угол а равен а = arctg ау/ах. Следует отметить, что составляющая вектора есть вектор, проекция вектора — число, которое может принимать положительное или отрицательное значения.
📺 Видео
Разложение вектора по 2 неколлинеарным векторам - bezbotvyСкачать

10 класс, 45 урок, Разложение вектора по трем некомпланарным векторамСкачать

89. Разложение вектора по двум неколлинеарным векторамСкачать

Геометрия 9 класс (Урок№7 - Разложение вектора по двум неколлинеарным векторам. Координаты вектора.)Скачать

Как разложить вектор по базису - bezbotvyСкачать

Разложение вектора по векторамСкачать

Разложение вектора по векторам (базису). Аналитическая геометрия-1Скачать

#вектор Разложение вектора по ортам. Направляющие косинусыСкачать

Разложение вектора по двум неколлинеарным векторам. Урок 4. Геометрия 9 классСкачать

Разложение вектора по двум неколлинеарным векторам - 1 часть. Геометрия 9Скачать

Разложение вектора по двум неколлинеарным векторам | Геометрия 7-9 класс #85 | ИнфоурокСкачать

РАЗЛОЖЕНИЕ ВЕКТОРА НА СОСТАВЛЯЮЩИЕСкачать

РАЗЛОЖЕНИЕ ВЕКТОРА по трем векторамСкачать

Разложение вектора по трем некомпланарным векторамСкачать

Выразить векторы. Разложить векторы. Задачи по рисункам. ГеометрияСкачать

Разложение вектора на неколлинеарные вектора.Скачать