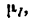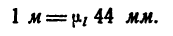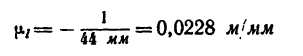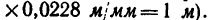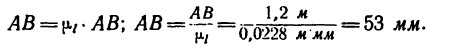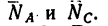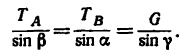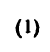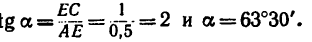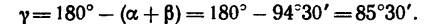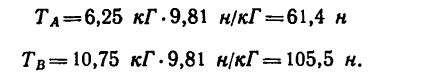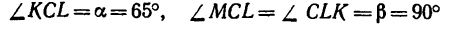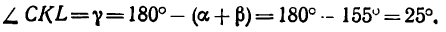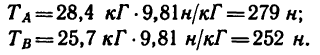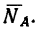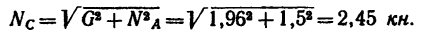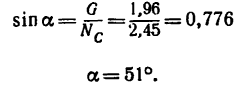1. Найти разность двух сил 5 и 10 ньютонов, направленных под углом 45 градусов друг к другу.
2. Канатоходец прогибает канат своим весом, равным 60 кг. Определить силу натяжения троса, если угол прогиба 120 градусов.
3. Найти проекции силы 150 ньютонов на координатные оси прямоугольной системы координат, если вектор силы направлен под углом 30 градусов к оси абсцисс.
- Краткая теория:
- Формулы для решения:
- где «альфа» — угол между вектором F и осью X.
- Алгоритм решения типовой задачи:
- Примеры решения:
- Законы сложения сил в механике
- Правило параллелограмма и правило многоугольника
- Разложение вектора силы по направлениям
- Разложение силы на две составляющие в теоретической механике
- 🎥 Видео
Краткая теория:
Ввиду того, что сила — вектор, вычитание сил проводится по правилам, принятым для векторов. Пусть надо вычесть силу F2 из силы F1.
Параллельным переносом начало силы F2 совмещаем с началом силы F1.
Из конца вектора F2 проводим вектор в конец вектора F1. Направление — от F2 к F1. Это и есть разность.
Разложение силы на составляющие по направлениям — операция, обратная нахождению равнодействующей. Технически она выполняется переносом направлений. Сумма составляющих должна давать исходный вектор.
Пусть задан вектор силы F. Надо разложить его на составляющие по заданным направлениям A и B.
Перенесем линии направлений A и B так, чтобы они прошли через конец вектора F. В полученной фигуре мы легко узнаем параллелограмм сил, построенный на составляющих FA и FB.
Проекции сил на оси координат можно считать частным случаем разложения на заданные направления. Оси координат, как правило, мы выбираем прямоугольными, что облегчает задачу. Проекции получают опусканием перпендикуляров на заданные оси координат. Проекции — скалярные величины, то есть они не имеют направления. Но каждой проекции приписывается знак «+» или «-«, в зависимости от направления исходного вектора относительно выбранных направлений осей.
Задан вектор силы F. Надо найти его проекции на выбранные оси прямоугольной системы координат.
Опускаем перпендикуляры на оси. Получаем проекции.
Формулы для решения:
где «альфа» — угол между вектором F и осью X.
Где «альфа» — угол между векторами
Алгоритм решения типовой задачи:
1. Кратко записываем условие задачи.
2. Изображаем условие графически.
3. Проводим графическое построение.
4. Проводим аналитический расчет.
5. Подставляем величины в общее решение, вычисляем.
6. Записываем ответ.
Примеры решения:
Задача 1.
Найти разность двух сил 5 и 10 ньютонов, направленных под углом 45 градусов друг к другу.
1. Кратко записываем условие задачи. Отметим, что в условии не сказано, какой вектор — уменьшаемое, а какой — вычитаемое. Поэтому разберем оба случая
а) Из первого вектора вычитается второй.
2. Изображаем условие графически.
3. Проводим графическое построение.
4. Проводим аналитический расчет.
5. Подставляем величины в общее решение, вычисляем.
Направление — от второго вектора к первому.
б) Из второго вектора вычитается первый
2. Изображаем условие графически.
3. Проводим графическое построение.
4,5. Проведение аналитического расчета и вычислений такое же, как и выше, но направление вектора разности — противоположное.
6. Ответ: Вектор разности в обоих случаях имеет величину 9,45 Н, направление в первом случае от второго вектора к первому, во втором случае — наоборот.
Задача 2.
Канатоходец прогибает канат своим весом, равным 60 кг. Определить силу натяжения троса, если угол прогиба 120 градусов.
1. Кратко записываем условие задачи.
2. Изображаем условие графически.
3. Проводим графическое построение. Равнодействующая двух сил «T» должна уравновешивать силу «F».
4. Проводим аналитический расчет. Треугольники, на которые разделился параллелограмм сил — равносторонние, так как они равнобедренные по построению, а вектор «F» делит угол пополам, то есть угол при основании равен 60 градусам. Таким образом, каждая из сил «T» равна силе «F».
5. Подставляем величины в общее решение, вычисляем.
T=60 кг. Переводим в систему СИ. В одном килограмме 9,8 ньютона. Поэтому:
6. Ответ: Сила натяжения троса 60 кг или 591 ньютон.
Задача 3.
Найти проекции силы 150 ньютонов на координатные оси прямоугольной системы координат, если вектор силы направлен под углом 30 градусов к оси абсцисс.
1. Кратко записываем условие задачи.
2. Изображаем условие графически.
3. Проводим графическое построение.
4. Проводим аналитический расчет.
5. Подставляем величины в общее решение, вычисляем.
6. Ответ: Проекция на ось абсцисс равна 129,5 ньютона, проекция на ось ординат равна 75 ньютонов.
Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Законы сложения сил в механике
При воздействии на одно тело нескольких сил одновременно тело начинает двигаться с ускорением, являющимся векторной суммой ускорений, которые бы возникли под воздействием каждой силы по отдельности. К действующим на тело силам, приложенным к одной точке, применяется правило сложения векторов.
Векторная сумма всех сил, одновременно воздействующих на тело, это сила равнодействующая, которая определяется по правилу векторного сложения сил:
R → = F 1 → + F 2 → + F 3 → + . . . + F n → = ∑ i = 1 n F i → .
Равнодействующая сила действует на тело также, как и сумма всех действующих на него сил.
Видео:#вектор Разложение вектора по ортам. Направляющие косинусыСкачать

Правило параллелограмма и правило многоугольника
Для сложения 2 -х сил используют правило параллелограмма (рисунок 1 ).
Рисунок 1 . Сложение 2 -х сил по правилу параллелограмма
Выведем формулу модуля равнодействующей силы с помощью теоремы косинусов:
R → = F 1 → 2 + F 2 → 2 + 2 F 1 → 2 F 2 → 2 cos α
При необходимости сложения более 2 -х сил используют правило многоугольника: от конца
1 -й силы необходимо провести вектор, равный и параллельный 2 -й силе; от конца 2 -й силы необходимо провести вектор, равный и параллельный 3 -й силе и т.д.
Рисунок 2 . Сложение сил правилом многоугольника
Конечный вектор, проведенный от точки приложения сил в конец последней силы, по величине и направлению равняется равнодействующей силе. Рисунок 2 наглядно иллюстрирует пример нахождения равнодействующей сил из 4 -х сил: F 1 → , F 2 → , F 3 → , F 4 → . Причем суммируемые векторы совсем необязательно должны быть в одной плоскости.
Результат действия силы на материальную точку будет зависеть только от ее модуля и направления. У твердого тела есть определенные размеры. Потому силы с одинаковыми модулями и направлениями вызывают разные движения твердого тела в зависимости от точки приложения.
Линией действия силы называют прямую, проходящую через вектор силы.
Рисунок 3 . Сложение сил, приложенных к различным точкам тела
Если силы приложены к различным точкам тела и действуют не параллельно по отношению друг к другу, тогда равнодействующая приложена к точке пересечения линий действия сил (рисунок 3 ). Точка будет находиться в равновесии, если векторная сумма всех сил, действующих на нее, равняется 0 : ∑ i = 1 n F i → = 0 → . В данном случае равняется 0 и сумма проекций данных сил на любую координатную ось.
Видео:Разложение силы на составляющиеСкачать

Разложение вектора силы по направлениям
Разложение сил на две составляющие – это замена одной силы 2 -мя, приложенными в той же точке и производящими на тело такое же действие, как и эта одна сила. Разложение сил осуществляется, как и сложение, правилом параллелограмма.
Задача разложения одной силы (модуль и направление которой заданы) на 2 , приложенные в одной точке и действующие под углом друг к другу, имеет однозначное решение в следующих случаях, когда известны:
- направления 2 -х составляющих сил;
- модуль и направление одной из составляющих сил;
- модули 2 -х составляющих сил.
Пример 1
Необходимо разложить силу F на 2 составляющие, находящиеся в одной плоскости с F и направленные вдоль прямых a и b (рисунок 4 ). Тогда достаточно от конца вектора F провести 2 прямые, параллельные прямым a и b . Отрезок F A и отрезок F B изображают искомые силы.
Рисунок 4 . Разложение вектора силы по направлениям
Второй вариант данной задачи – найти одну из проекций вектора силы по заданным векторам силы и 2 -й проекции (рисунок 5 а ).
Рисунок 5 . Нахождение проекции вектора силы по заданным векторам
Во втором варианте задачи необходимо построить параллелограмм по диагонали и одной из сторон, как в планиметрии. На рисунке 5 б изображен такой параллелограмм и обозначена искомая составляющая F 2 → силы F → .
Итак, 2 -й способ решения: прибавим к силе силу, равную — F 1 → (рисунок 5 в ). В итоге получаем искомую силу F → .
Три силы F 1 → = 1 Н ; F 2 → = 2 Н ; F 3 → = 3 Н приложены к одной точке, находятся в одной плоскости (рисунок 6 а ) и составляют углы с горизонталью α = 0 ° ; β = 60 ° ; γ = 30 ° соответственно. Необходимо найти равнодействующую силу.
Решение
Рисунок 6 . Нахождение равнодействующей силы по заданным векторам
Нарисуем взаимно перпендикулярные оси О Х и O Y таким образом, чтобы ось О Х совпадала с горизонталью, вдоль которой направлена сила F 1 → . Сделаем проекцию данных сил на координатные оси (рисунок 6 б ). Проекции F 2 y и F 2 x отрицательны. Сумма проекций сил на координатную ось О Х равняется проекции на данную ось равнодействующей: F 1 + F 2 cos β — F 3 cos γ = F x = 4 — 3 3 2 ≈ — 0 , 6 Н .
Точно также для проекций на ось O Y : — F 2 sin β + F 3 sin γ = F y = 3 — 2 3 2 ≈ — 0 , 2 Н .
Модуль равнодействующей определим с помощью теоремы Пифагора:
F = F x 2 + F y 2 = 0 , 36 + 0 , 04 ≈ 0 , 64 Н .
Направление равнодействующей найдем при помощи угла между равнодействующей и осью (рисунок 6 в ):
t g φ = F y F x = 3 — 2 3 4 — 3 3 ≈ 0 , 4 .
Сила F = 1 к Н приложена в точке В кронштейна и направлена вертикально вниз (рисунок 7 а ). Необходимо найти составляющие данной силы по направлениям стержней кронштейна. Все необходимые данные отображены на рисунке.
Решение
Рисунок 7 . Нахождение составляющих силы F по направлениям стержней кронштейна
Дано:
F = 1 к Н = 1000 Н
Пускай стержни прикручены к стене в точках А и С . На рисунке 7 б изображено разложение силы F → на составляющие вдоль направлений А В и В С . Отсюда понятно, что
F 1 → = F t g β ≈ 577 Н ;
F 2 → = F cos β ≈ 1155 Н .
Ответ: F 1 → = 557 Н ; F 2 → = 1155 Н .
Видео:Разложение вектора по базису. 9 класс.Скачать

Разложение силы на две составляющие в теоретической механике
Разложение силы на две составляющие:
Решение многих практических задач по статике сводится к разложению силы на две составляющие. Подобные задачи решаются либо по правилу параллелограмма, либо по правилу треугольника и, в зависимости от исходных данных, приводятся к одному из четырех типов.
Общая методика решения приведенных ниже задач сводится к следующему:
- Выбираем метод решения — графический или графо-аналитический.
- Выбираем правило, по которому будем решать задачу, т. е. либо правило параллелограмма, либо правило треугольника.
- Если выбран графический метод, то далее выбираем масштаб построения, строим параллелограмм или треугольник (в соответствии с выбранным правилом) и, наконец, измеряем стороны получившейся фигуры, находим модули соответствующих сил, а измерив углы, найдем их направления.
- Если выбран графо-аналитический метод, то в зависимости от избранного правила строим параллелограмм или треугольник, соблюдая приблизительные соотношения размеров длин и углов, а затем, в зависимости от исходных данных, используем геометрические или тригонометрические соотношения.
Задача №1
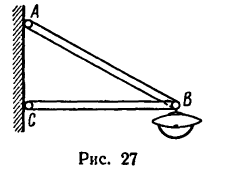
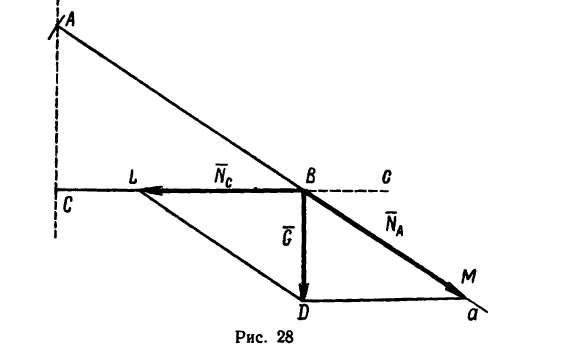
Фонарь весом 80 н подвешен на кронштейне АВС, укрепленном на вертикальной стене (рис. 27). Определить усилия, возникшие в горизонтальном стержне СВ и наклонной тяге АВ после подвески фонаря, если СВ = 1 ли /AB = 1,2 л. Соединения в точках А, В и С кронштейна — шарнирные.
Решение 1—графическим методом по правилу параллелограмма.
1. Если избран графический метод решения, то прежде всего необходимо в масштабе построить кронштейн АВС. Выполнение чертежа кронштейна сводится, как это следует из формы и размеров, заданных в условии задачи, к построению прямоугольного треугольника по двум заданным сторонам.
2. Построим кронштейн в масштабе «1 м в 44 мм». Обозначив масштаб чертежа
Отсюда масштаб построения кронштейна
3. Из произвольной точки С (рис. 28) проводим горизонтальную и вертикальную линии. На горизонтальной линии отложим
отрезок ВС = 44 мм, который в выбранном масштабе и изобразит горизонтальный стержень кронштейна
Длина отрезка АВ, который изобразит тягу АВ, определяется из равенства
Найденную длину АВ = 53 мм отложим при помощи циркуля из точки В так, чтобы получить точку А на вертикали, проведенной ранее из точки С. Построенный треугольник АВС изображает данный в условии задачи кронштейн.
4. Строим параллелограмм сил, действующих на точку В кронштейна.
Вес фонаря G = 80 н, действующий на кронштейн вертикально вниз, изобразим отрезком BD=20 мм. Значит масштаб построения
для сил 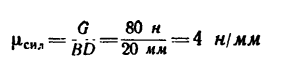
(4 н в 1 мм).
Благодаря тому что в точках А, В и С кронштейна соединения шарнирные, стержни, находясь под действием веса фонаря, либо растягиваются, либо сжимаются. Иными словами, искомые усилия действуют вдоль стержней. Значит направления сил известны (1-й тип задачи на разложения силы по правилу параллелограмма).
Изобразим направление действия искомых сил линиями Аа и Сс, пересекающимися в точке В — точке приложения к кронштейну веса фонаря.
Из точки D (конца вектора 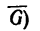
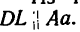
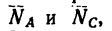
5. При помощи масштабной линейки измерим отрезки ВМ и BL:
ВМ=36 мм и BL—30 мм.
Следовательно, 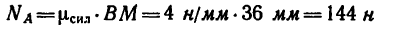
и 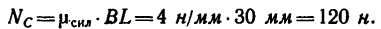
Как видно из получившегося на рис. 28 построения, тяга АВ кронштейна растягивается силой, равной 144 н, а стержень ВС сжимается силой 120 н.
Решение 2—графо-аналитическим методом по правилу параллелограмма с использованием геометрических соотношений.
1. Используя рис. 27, на котором изображен кронштейн, строим параллелограмм сил. Через произвольную точку а (рис. 29) проводим прямые 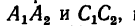
Из той же точки а откладываем вертикально вниз отрезок ab, который изображает силу 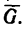
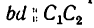
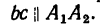
2. Теперь имеются две геометрические фигуры — треугольник АВС (см. рис. 27), изображающий заданный кронштейн, и силовой параллелограмм (см. рис. 29).
Геометрически 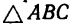
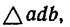
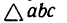
Используя свойство подобных треугольников (замечаем, что db = ac—Nc), получаем
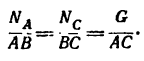
3. Решая получившиеся пропорции, находим 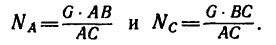
Неизвестную в кронштейне длину АС найдем по теореме Пнфагора (из условия задачи ясно, что угол АСВ — прямой)
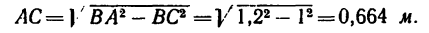
Подставляя в выражения для 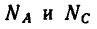
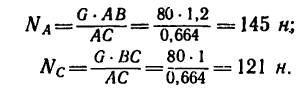
Таким образом, результат практически тот же, что и при графическом решении. Некоторое расхождение объясняется меньшей точностью графического решения.
Как уже известно, графо-аналитическое решение задачи 22-6 основано на подобии двух треугольников: кронштейна, имеющего вид треугольника, и силового треугольника. Но возможен случай, когда на чертеже нагруженного устройства или конструкции не будет треугольника, подобного силовому. Тогда для решения задачи целесообразно применить графо-аналитический метод с использованием тригонометрических соотношений.
Рассмотрим такую задачу.
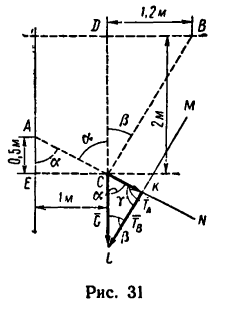
Задача №2
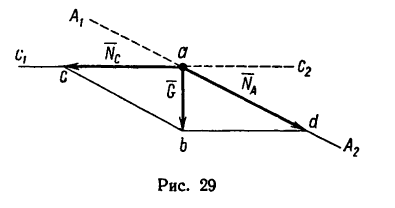
При помощи двух нерастяжимых нитей АС и ВС удерживается груз, вес которого 12 кГ. Положение нитей и груза показано на рис. 30. Определить натяжение нитей.
Решение 1 — графо-аналитическим методом по правилу треугольника с использованием тригонометрии.
1. Так же, как и в предыдущей задаче, необходимо силу G=12 кГ разложить на две составляющие, линии действия которых совпадают с направлениями линий АС и ВС.
2. Изобразим силу 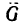
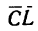
3. Если в треугольнике CKL известны углы а, 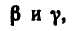
4. Из построения силового треугольника следует, что 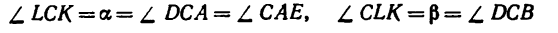
(для наглядности положение нитей относительно вектора G показано на рис. 31 штриховой линией). А так как треугольники 


Из 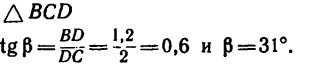
Угол у легко найдем как дополнение к 
5. И теперь, зная углы а, 
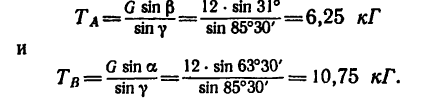
Таким образом, нить С А растягивается усилием, равным 6,25 кГ, а нить СВ — усилием 10,75 кГ.
Если эти усилия выразить в единицах СИ, то
и
Задачу просто решить графическим методом. Для этого нужно начертить в масштабе расположение нитей и, выбрав масштаб для сил (например, 0,2 кГ/мм), построить на векторе G силовой треугольник и, измерив его стороны, найти
Графо-аналитический метод с использованием свойств подобных треугольников целесообразно применять к решению таких задач в том случае, если в схеме конструкции или устройства имеется треугольник, подобный силовому.
Если же в схеме конструкции нет треугольника, подобного силовому, то решение графо-аналитическим методом целесообразнее производить с использованием тригонометрических свойств, потому что при наличии линейных размеров необходимые для решения задачи значения углов, как правило, найти очень просто.
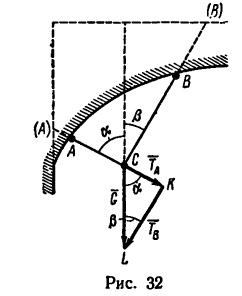
Необходимо отметить, что в задачах, подобных 22-6 и 23-6, усилия, вызываемые нагрузкой в стержнях кронштейнов или нитях устройств, удерживающих груз, не зависят от длины этих нитей или стержней.
Допустим, что груз (задача 23-6) удерживается нитями, прикрепленными не к вертикальной стенке и горизонтальному потолку, как на рис, 30, а к двум точкам криволинейной (сводчатой) поверхности (рис. 32). Но если при этом углы аи
Задача №3
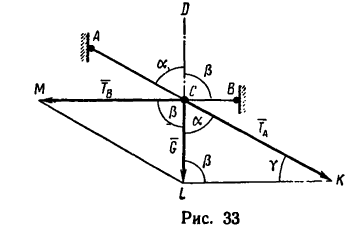
Груз весом G= 12 кГ удерживается при помощи двух нитей, которые образуют с вертикалью (линией действия веса G) углы а=65° и 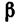
Решение—графо-аналитическим методом по правилу параллелограмма.
1. Исходя из условия задачи, построим чертеж (рис. 33). Из точки С проводим вертикальный отрезок CL, изображающий вектор 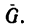
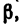
2. Вектор 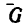
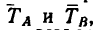
3. На основе построения параллелограмма CKLM очень просто определяются его углы:
4. Так как силовой параллелограмм делится на два прямоугольных треугольника, то легко найти оба усилия: 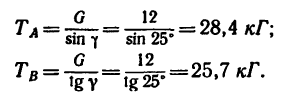
единицах СИ усилия равны:
Задачи 6 относятся к первому типу задач на разложение силы по правилу параллелограмма или треугольника.
Рассмотрим теперь по одной задаче второго (задача 25-6), третьего (задача 26-6) и четвертого (задача 27-6) типов.
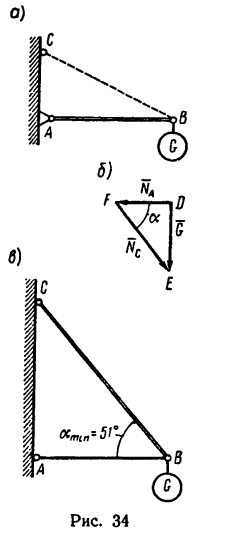
Задача №4
Груз массой 200 кг необходимо подвесить на кронштейне, у которого один из стержней горизонтальный и в нем должно возникнуть сжимающее усилие не более 1,5 кн.
Как нужно расположить второй стержень, чтобы в нем возникло растягивающее усилие? Определить величину этого усилия.
Эта задача аналогична задаче 8-2, которая решена графическим методом, поэтому графическое решение здесь не приводим.
Решение —графо-аналитическим методом по правилу треугольника.
1. Изобразим (рис. 34, а) стержень АВ в горизонтальном положении, т. е. в том, какое он должен занимать по условию, и допустим, что к концу В стержня приложена нагрузка 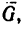
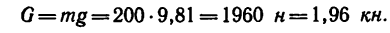
Известно, что этот стержень должен испытывать сжимающее усилие 1,5 кн. Поэтому сила, приложенная к стержню в точке В, будет направлена от В к А. Обозначим эту силу
Расположение стержня ВС кронштейна неизвестно и поэтому он условно показан штриховой линией.
2. Строим силовой треугольник (рис. 34, б). Из произвольной точки D отложим вертикальный отрезок DE, изображающий вес груза 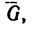
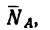
Для того чтобы найти второе слагаемое вектора 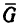
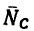
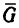
Чтобы выполнить это действие по правилу треугольника, соединим точки F и Е. Сторона FE получившегося треугольника изображает искомое усилие 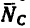
3. Треугольник DEF прямоугольный, поэтому
Если мысленно в точку В кронштейна перенести силу 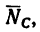
Угол АВС (рис. 34, в) между стержнями должен быть равен углу между линиями действия сил 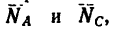
и
Таким образом, если в кронштейне стержень ВС расположить к горизонтальному стержню В А под углом а=51°, то груз весом G = l,96 кн, действующий на точку В кронштейна, вызовет в стержне В А сжимающее усилие 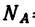
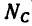
Если при изготовлении кронштейна увеличить угол a(a>51°), то уменьшится нагрузка на оба стержня, причем при вертикальном положении стержня ВС (а = 90°) усилие 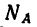
Если же при изготовлении кронштейна угол а уменьшить (а 51° или а
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
🎥 Видео
Как разложить силы на проекции (динамика 10-11 класс) ЕГЭ по физикеСкачать

Физика | Ликбез по векторамСкачать

Урок 8. Векторные величины. Действия над векторами.Скачать

Равнодействующая и сложение силСкачать

Найдите разложение вектора по векторам (базису)Скачать

Выразить векторы. Разложить векторы. Задачи по рисункам. ГеометрияСкачать

89. Разложение вектора по двум неколлинеарным векторамСкачать

9 класс, 1 урок, Разложение вектора по двум неколлинеарным векторамСкачать

Урок 38 (осн). Сложение сил, направленных по одной прямой. РавнодействующаяСкачать

Разложение вектора по векторам (базису). Аналитическая геометрия-1Скачать

РАЗЛОЖЕНИЕ ВЕКТОРА по трем векторамСкачать

Разложение силы на составляющиеСкачать

18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Разложение вектора по векторамСкачать

Геометрия 9 класс (Урок№7 - Разложение вектора по двум неколлинеарным векторам. Координаты вектора.)Скачать

Математика без Ху!ни. Смешанное произведение векторовСкачать