Статья содержит два калькулятора, рассчитывающие параметры деления круга на равные по площади части радиусами и параллельными хордами
Ниже представлены два калькулятора, рассчитывающие параметры разделения круга на равные части. Сначала — традиционный калькулятор, который делит круг на равные части радиусами (примерно так, как режут пиццу или торт), под ним — нетрадиционный калькулятор, который делит круг на равные по площади части параллельными хордами. Оба калькулятора визуализируют результат рисунком. Методы расчета с формулами для обоих калькуляторов приведены ниже, под калькуляторами.
- Деление круга на равные по площади части радиусами
- Деление круга на равные по площади части параллельными хордами
- Деление круга на равные части радиусами
- Деление круга на равные части параллельными хордами
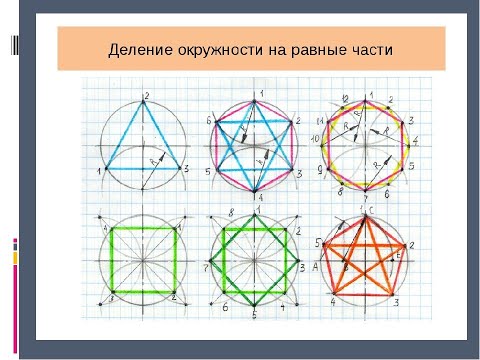
- Деление окружности на равные части
- Деление окружности на шесть равных частей
- Деление окружности на восемь равных частей
- Деление окружности на любое число равных частей
- Нахождение центра дуги и определение величины радиуса
- Сопряжения
- Деление окружности на равные части — Ответы (ГДЗ) к рабочей тетради по математике 3 класс 2 часть (Рудницкая, Юдачева)
- 🔍 Видео
Деление круга на равные по площади части радиусами
Деление круга на равные по площади части параллельными хордами
Деление круга на равные части радиусами
Традиционный и очень простой метод деления круга — по факту, нарезка равных секторов. Метод и формулы очень просты:
- Определяем угловой размер каждого сектора в радианах, путем деления 360 градусов на нужное число секторов.
- Определяем размер дуги сектора, перемножая радиус на угол в радианах
- Определяем размер хорды по теореме косинусов (хорда является основанием равнобедренного треугольника с боковыми сторонами R и противолежащим углом альфа.
Собственно и всё — мы получили все характеристики для N равных секторов
Деление круга на равные части параллельными хордами
Этот способ более любопытен, чем предыдущий. Для простоты будем рассматривать верхнюю половину круга, так как с нижней все будет симметрично.
Задача состоит в определении x-вой координаты точек, через которые нужно проводить хорды (на рисунке это точки x1 и x2). Выведем для начала формулу площади куска, отсекаемого хордой слева.
Верхнюю полуокружность можно представить графиком функции y=f(x), где x — это координата вдоль оси абсцисс, а y — это функция, численно равная y координате соответствующей точки верхней полуокружности.
По теореме Пифагора получаем следующую функцию
Чтобы получить площадь фигуры, отсекаемой хордой слева, надо проинтегрировать эту функцию от -R до x. Первообразная функции равна:
Осталось определиться с константой. Нам надо, чтобы в точке с координатами -R площадь была равна нулю. Подставив -R вместо x в формулу выше, получаем
Итак, полное выражение
Теперь рассмотрим нахождение координат крайней левой точки. Нам известна площадь, которую она должна отсечь (напоминаю, речь идет о полуокружности)
Таким образом мы можем приравнять
Что дает нам такое финальное уравнение
Данное уравнение является трансцендентным, а поэтому находить координату первой точки придется численным методом, например, методом бисекции или методом Ньютона. Калькулятор использует метод Ньютона.
Вторая и последующие точки находится аналогично, путем изменения размера отсекаемой площади. Для второй точки это будет , для третьей и так далее.
Зная координаты точек, несложно рассчитать все остальные параметры, в частности, длину хорды.
Видео:Деление окружности на равные части с помощью циркуляСкачать

Деление окружности на равные части
Деление окружности на три равные части. Устанавливают угольник с углами 30 и 60° большим катетом параллельно одной из центровых линий. Вдоль гипотенузы из точки 1 (первое деление) проводят хорду (рис. 2.11, а), получая второе деление – точку 2. Перевернув угольник и проведя вторую хорду, получают третье деление – точку 3 (рис. 2.11, б). Соединив точки 2 и 3; 3 и 1 прямыми, получают равносторонний треугольник.
Рис. 2.11. Деление окружности на три равные части:
а, б – с помощью угольника; в – с помощью циркуля
Ту же задачу можно решить с помощью циркуля. Поставив опорную ножку циркуля в нижний или верхний конец диаметра (рис. 2.11, в), описывают дугу, радиус которой равен радиусу окружности. Получают первое и второе деления. Третье деление находится на противоположном конце диаметра.
Видео:ПОСТРОИТЬ ПРАВИЛЬНЫЙ 14-УГОЛЬНИК [construction of regular tetradecagon]Скачать
![ПОСТРОИТЬ ПРАВИЛЬНЫЙ 14-УГОЛЬНИК [construction of regular tetradecagon]](https://i.ytimg.com/vi/Yi0t67972YY/0.jpg)
Деление окружности на шесть равных частей
Раствор циркуля устанавливают равным радиусу R окружности. Из концов одного из диаметров окружности (из точек 1, 4) описывают дуги (рис. 2.12, а, б). Точки 1, 2, 3, 4, 5, 6 делят окружность на шесть равных частей. Соединив их прямыми, получают правильный шестиугольник (рис. 2.12, б).
Рис. 2.12. Деление окружности на шесть равных частей с помощью циркуля
Ту же задачу можно выполнить с помощью линейки и угольника с углами 30 и 60° (рис. 2.13). Гипотенуза угольника при этом должна проходить через центр окружности.
Рис. 2.13. Деление окружности на шесть равных частей с помощью угольника
Видео:Деление окружности на n- равные частиСкачать

Деление окружности на восемь равных частей
Точки 1, 3, 5, 7 лежат на пересечении центровых линий с окружностью (рис. 2.14). Еще четыре точки находят с помощью угольника с углами 45°. При получении точек 2, 4, 6, 8 гипотенуза угольника проходит через центр окружности.
Рис. 2.14. Деление окружности на восемь равных частей с помощью угольника
Видео:КАК РАЗДЕЛИТЬ ОКРУЖНОСТЬ НА 12 РАВНЫХ ЧАСТЕЙ?Скачать

Деление окружности на любое число равных частей
Для деления окружности на любое число равных частей пользуются коэффициентами, приведенными в табл. 2.1.
Длину l хорды, которую откладывают на заданной окружности, определяют по формуле l = dk, где l – длина хорды; d – диаметр заданной окружности; k – коэффициент, определяемый по табл. 1.2.
Коэффициенты для деления окружностей
Число делений п
Число делений п
Чтобы разделить окружность заданного диаметра 90 мм, например, на 14 частей, поступают следующим образом.
В первой графе табл. 2.1 находят число делений п, т.е. 14. Из второй графы выписывают коэффициент k, соответствующий числу делений п. В данном случае он равен 0,22252. Диаметр заданной окружности умножают на коэффициент и получают длину хорды l= dk = 90 • 0,22252 = 0,22 мм. Полученную длину хорды откладывают циркулем-измерителем 14 раз на заданной окружности.
Видео:деление окружности на произвольное число частейСкачать
Нахождение центра дуги и определение величины радиуса
Задана дуга окружности, центр и радиус которой неизвестны.
Для их определения нужно провести две непараллельные хорды (рис. 2.15, а) и восставить перпендикуляры к серединам хорд (рис. 2.15, б). Центр О дуги находится на пересечении этих перпендикуляров.
Рис. 2.15. Определение центра дуги
Видео:Построение шестнадцатиугольника циркулемСкачать

Сопряжения
При выполнении машиностроительных чертежей, а также при разметке заготовок деталей на производстве часто приходится плавно соединять прямые линии с дугами окружностей или дугу окружности с дугами других окружностей, т.е. выполнять сопряжение.
Сопряжением называют плавный переход прямой в дугу окружности или одной дуги в другую.
Для построения сопряжений надо знать величину радиуса сопряжений, найти центры, из которых проводят дуги, т.е. центры сопряжений (рис. 2.16). Затем нужно найти точки, в которых одна линия переходит в другую, т.е. точки сопряжений. При построении чертежа сопрягающиеся линии нужно доводить точно до этих точек. Точка сопряжения дуги окружности и прямой лежит на перпендикуляре, опущенном из центра дуги на сопрягаемую прямую (рис. 2.17, а), или на линии, соединяющей центры сопрягаемых дуг (рис. 2.17, б). Следовательно, для построения любого сопряжения дугой заданного радиуса нужно найти центр сопряжения и точку (точки) сопряжения.
Рис. 2.16. Элементы сопряжений
Рис. 2.17. Определение точки сопряжения
Сопряжение двух пересекающихся прямых дугой заданного радиуса. Даны пересекающиеся под прямым, острым и тупым углами прямые линии (рис. 2.18, а). Нужно построить сопряжения этих прямых дугой заданного радиуса R.
Рис. 2.18. Построение сопряжения двух пересекающихся прямых
Для всех трех случаев можно применять следующее построение.
1. Находят точку О – центр сопряжения, который должен лежать на расстоянии R от сторон угла, т.е. в точке пересечения прямых, проходящих параллельно сторонам угла на расстоянии R от них (рис. 2.18, б).
Для проведения прямых, параллельных сторонам угла, из произвольных точек, взятых на прямых, раствором циркуля, равным R, делают засечки и к ним проводят касательные (рис. 2.18, б).
- 2. Находят точки сопряжений (рис. 2.18, в). Для этого из точки О опускают перпендикуляры на заданные прямые.
- 3. Из точки О, как из центра, описывают дугу заданного радиуса R между точками сопряжений (рис. 2.18, в).
Видео:Деление окружности на 12 равных частейСкачать

Деление окружности на равные части — Ответы (ГДЗ) к рабочей тетради по математике 3 класс 2 часть (Рудницкая, Юдачева)
УЗНАЕМ НОВОЕ
14. Раздели каждую окружность на две равные части с помощью линейки.
15. Построй окружность с центром в точке О и радиусом 2 см. Раздели ее точками A, B, C и D на четыре равные части.
16. Точки P, K, F, M делят данную окружность на четыре равные части. Найди центра окружности и обозначь его буквой О.
17. Раздели с помощью циркуля каждую окружность на шесть равных частей.
18. Точки, отмеченные на каждой окружности, деляет ее на шесть равных частей. Выдели красным карандашом три точки, которые делят окружность на три равные части.
19. Раскрась многоугольник, все вершины которого лежат на окружности.
20. Данную окружность раздели точками М, К, С, В, Р, А на шесть равных частей. Постой шестиугольник МКСВРА.
21. Запиши обозначения многоугольников, вершины которых лежат на окружности.
ВСПОМИНАЕМ ПРОЙДЕННОЕ
22. Запиши результаты действий.
23. Вычисли устно и запиши ответ.
24. Из книги выпало несколько листов с такими номерами страниц. Запиши, в каком порядке нужно подклеить в книгу выпавшие листы.
325, 327, 329, 331, 333.
25.
Запиши, что можно узнать, вычислив значение каждого из выражений. Вычисли.
26. Выполни действия.
27. Выпиши и запиши синим карандашом верные высказывания.
28. Школьники помогали собирать урожай. В поле работали 152 ученика, на огороде — на 25 меньше, а в саду на 88 учеников больше, чем на огороде.
Придумай такой вопрос, чтобы задача решалась в три действия. Реши ее.
🔍 Видео
Деление окружности на 3; 6; 12 равных частейСкачать

Как разделить окружность на 10 частей How to divide a circle into 10 partsСкачать

Деление окружности на 5 равных частейСкачать
Деление окружности на 5 частей с помощью циркуляСкачать
Деление окружности на N равных частей. Урок 8. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Построение девятиугольника циркулем, приближенноеСкачать

Красивое деление окружности на 20 частей циркулемСкачать

1 2 2 деление окружности на 5 равных частейСкачать

КАК РАЗДЕЛИТЬ ОКРУЖНОСТЬ КРУГ НА 4 РАВНЫЕ ЧАСТИ С ПОМОЩЬЮ ЦИРКУЛЯ И ЛИНЕЙКИ ? ЛЕГКО !Скачать

Деление окружности на 3, 4, 5, 6 и 7 равных частейСкачать

Деление окружности на 3 частиСкачать

1 2 3 деление окружности на 7 равных частейСкачать

Построение 10 угольника циркулемСкачать






















